八年级数学上册试题 15.4.1 角平分线的尺规作图-沪科版(含答案)
文档属性
| 名称 | 八年级数学上册试题 15.4.1 角平分线的尺规作图-沪科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 379.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 18:55:11 | ||
图片预览



文档简介
15.4.1 角平分线的尺规作图
一、单选题
1.如图,直线l分别与直线AB、CD相交于点E、F,EG平分∠BEF交直线CD于点G,若∠1=∠BEF,若EF=3,则FG为( )
A.4 B.3 C.5 D.1.5
2.如图,,点,分别是射线,上的动点,的平分线和的平分线所在直线相交于点,则的大小为( )
A.45° B.50° C.60° D.随点,的移动而变化
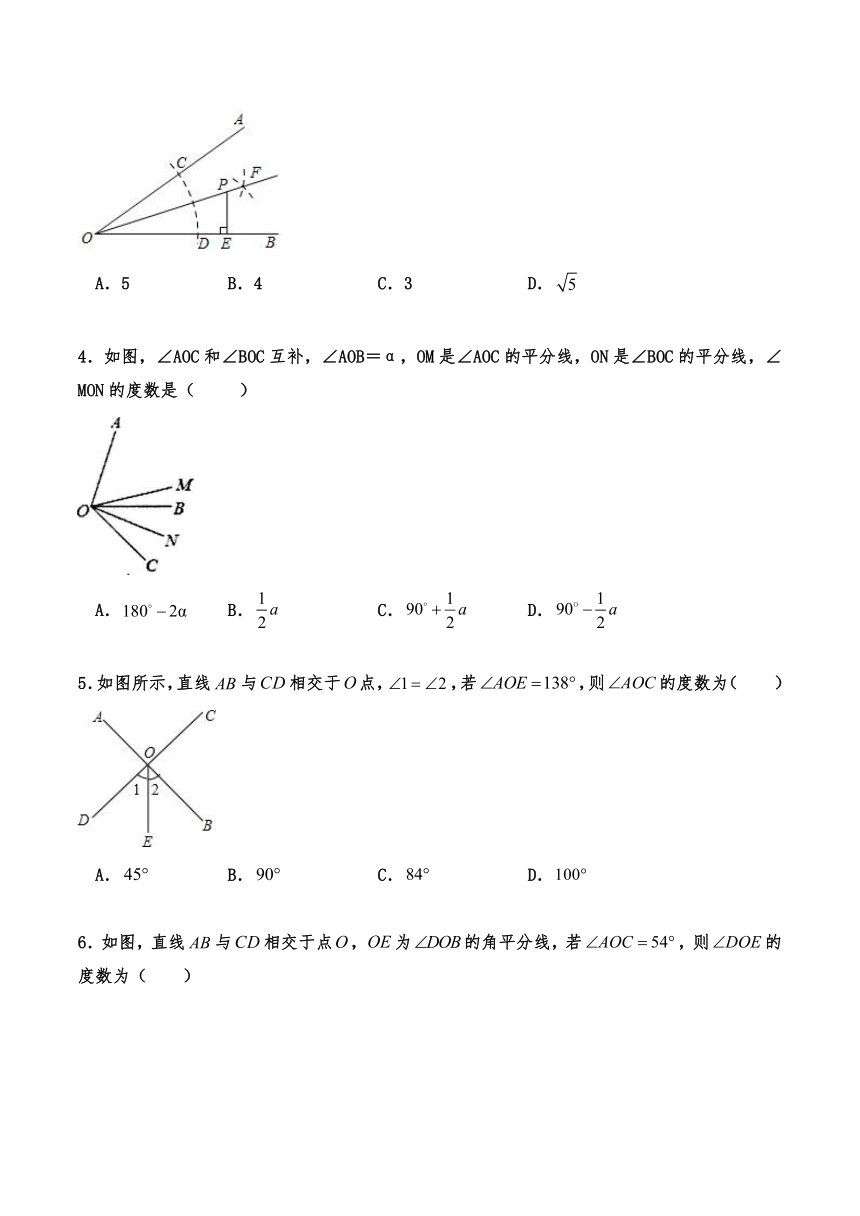
3.如图,已知∠AOB,以点O为圆心,任意长为半径画弧,交OA于点C,交OB于点D,再分别以C,D为圆心,以大于CD长为半径画弧,两弧交于点F,作射线OF,点P为OF上一点,PE⊥OB,垂足为点E,若PE=5,则点P到OA的距离为( )
A.5 B.4 C.3 D.
4.如图,∠AOC和∠BOC互补,∠AOB=α,OM是∠AOC的平分线,ON是∠BOC的平分线,∠MON的度数是( )
A. B. C. D.
5.如图所示,直线与相交于点,,若,则的度数为( )
A. B. C. D.
6.如图,直线与相交于点,为的角平分线,若,则的度数为( )
A. B. C. D.
7.如图,与互余,与互补,平分,则的度数是( )
A. B. C. D.
8.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A.15 B.30 C.45 D.60
二、填空题
9.已知:如图,点O为直线AB上一点,OC是AOB的平分线,OD在∠BOC内看图填空(选填“<”、“>”或“=”):∠AOD___________ ∠BOC
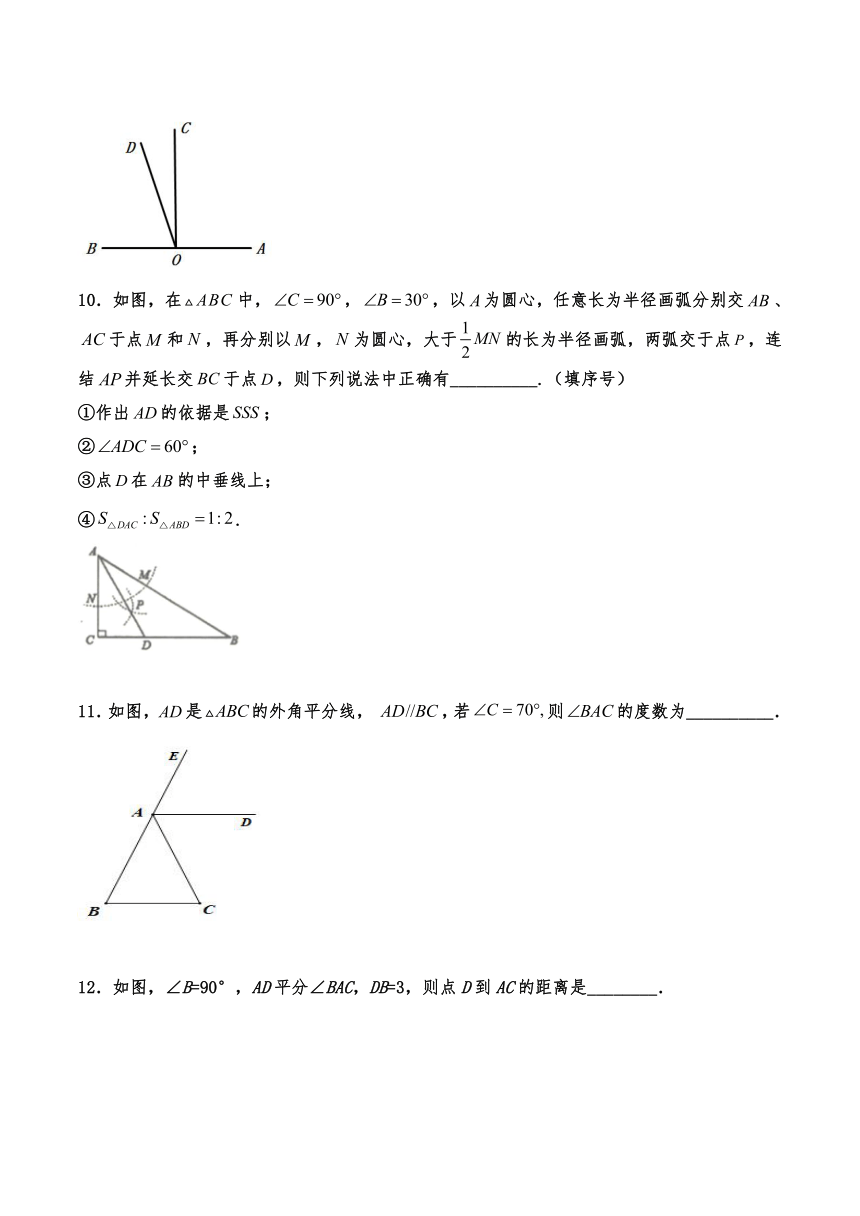
10.如图,在中,,,以为圆心,任意长为半径画弧分别交、于点和,再分别以,为圆心,大于的长为半径画弧,两弧交于点,连结并延长交于点,则下列说法中正确有__________.(填序号)
①作出的依据是;
②;
③点在的中垂线上;
④.
11.如图,是的外角平分线, ,若则的度数为__________.
12.如图,∠B=90°,AD平分∠BAC,DB=3,则点D到AC的距离是________.
13.OB是∠AOC内部的一条射线,把三角形的角的顶点放在点O处,转动三角尺,当三角尺的边OD平分∠AOB, 三角尺的另一边OE也正好平分∠BOC, 则∠AOC的度数为________
14.已知射线OP是∠AOB的角平分线,若∠AOB=100°,则∠AOP的度数等于_____________°.
三、解答题
15.校园的一角如图所示,其中线段,,表示围墙,围墙内是学生的一个活动区域,小明想在图中的活动区域中找到一点,使得点到三面围墙的距离都相等.请在图中找出点.(用尺规作图,不用写作法,保留作图痕迹)
16.BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE,则EF也是∠AED的平分线.
完成下列推理过程:
∵BD是∠ABC的平分线,
∴∠ABD=∠DBC(_____________________________________)
∵ED∥BC(已知)
∴∠BDE=∠DBC(_________________________________)
∴∠ABD=∠BDE,
又∵∠FED=∠BDE(_____)
∴EF∥BD(_________________________________),
∴∠AEF=∠ABD(_________________________________)
∴∠AEF=∠FED(_________________________________),
∴EF是∠AED的平分线
17.已知:如图,.平分.
(1)求证:;
(2)求的度数.
18.如图,已知平分,求的度数.
19.(1)完成下面的证明.
如图,在四边形中,,是的平分线.求证:.
证明:是的平分线(已知)
__________________(角平分线的定义)
又(已知)
__________________(等量代换)
(____________________________)
(2)已知线段,是的中点,在直线上,且,画图并计算的长.
答案
一、单选题
B.B.A.B.C.C.B.B.
二、填空题
9.>
10.①②③④.
11.40°.
12.
13.120°
14.50.
三、解答题
15.
解:分别作的角平分线,如图,
∴交点P即为所求.
16.∵BD是∠ABC的平分线,
∴∠ABD=∠DBC(角平分线定义)
∵ED∥BC(已知)
∴∠BDE=∠DBC(两条直线平行,内错角相等)
∴∠ABD=∠BDE,
又∵∠FED=∠BDE(已知)
∴EF∥BD(内错角相等,两条直线平行),
∴∠AEF=∠ABD(两条直线平行,同位角相等)
∴∠AEF=∠FED(等量代换),
∴EF是∠AED的平分线
17.
解:(1)证明:,
,
;
(2)由(1)得
平分
18.
∵∠AOB=90°,∠BOC=40°,
∴∠AOC=90°+40°=130°,
∵OD平分∠AOC,
∴∠DOC=130°÷2=65°,
∴∠BOD=∠DOC-∠BOC=25°.
19.解:(1)平分(已知)
.(角平分线的定义)
(已知)
. (等量代换)
.(内错角相等,两直线平行)
故答案为1,3,2,3,内错角相等,两直线平行;
(2),是的中点
①当点D在线段AB上时,CD=CB-DB=6-2=4cm;
②当点D在线段AB的延长线上时,CD=CB+BD=6+2=8cm;
综上所述,CD的长为4cm或8cm.
20.
解:∵∠COD=116°,∠BOD=90°,
∴∠BOC=∠COD-∠BOD=116°-90°=26°,
∵OA平分∠BOC,
∴∠AOB=∠BOC÷2=13°,
∴∠AOD=∠BOD-∠AOB=90°+13°=103°
一、单选题
1.如图,直线l分别与直线AB、CD相交于点E、F,EG平分∠BEF交直线CD于点G,若∠1=∠BEF,若EF=3,则FG为( )
A.4 B.3 C.5 D.1.5
2.如图,,点,分别是射线,上的动点,的平分线和的平分线所在直线相交于点,则的大小为( )
A.45° B.50° C.60° D.随点,的移动而变化
3.如图,已知∠AOB,以点O为圆心,任意长为半径画弧,交OA于点C,交OB于点D,再分别以C,D为圆心,以大于CD长为半径画弧,两弧交于点F,作射线OF,点P为OF上一点,PE⊥OB,垂足为点E,若PE=5,则点P到OA的距离为( )
A.5 B.4 C.3 D.
4.如图,∠AOC和∠BOC互补,∠AOB=α,OM是∠AOC的平分线,ON是∠BOC的平分线,∠MON的度数是( )
A. B. C. D.
5.如图所示,直线与相交于点,,若,则的度数为( )
A. B. C. D.
6.如图,直线与相交于点,为的角平分线,若,则的度数为( )
A. B. C. D.
7.如图,与互余,与互补,平分,则的度数是( )
A. B. C. D.
8.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A.15 B.30 C.45 D.60
二、填空题
9.已知:如图,点O为直线AB上一点,OC是AOB的平分线,OD在∠BOC内看图填空(选填“<”、“>”或“=”):∠AOD___________ ∠BOC
10.如图,在中,,,以为圆心,任意长为半径画弧分别交、于点和,再分别以,为圆心,大于的长为半径画弧,两弧交于点,连结并延长交于点,则下列说法中正确有__________.(填序号)
①作出的依据是;
②;
③点在的中垂线上;
④.
11.如图,是的外角平分线, ,若则的度数为__________.
12.如图,∠B=90°,AD平分∠BAC,DB=3,则点D到AC的距离是________.
13.OB是∠AOC内部的一条射线,把三角形的角的顶点放在点O处,转动三角尺,当三角尺的边OD平分∠AOB, 三角尺的另一边OE也正好平分∠BOC, 则∠AOC的度数为________
14.已知射线OP是∠AOB的角平分线,若∠AOB=100°,则∠AOP的度数等于_____________°.
三、解答题
15.校园的一角如图所示,其中线段,,表示围墙,围墙内是学生的一个活动区域,小明想在图中的活动区域中找到一点,使得点到三面围墙的距离都相等.请在图中找出点.(用尺规作图,不用写作法,保留作图痕迹)
16.BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE,则EF也是∠AED的平分线.
完成下列推理过程:
∵BD是∠ABC的平分线,
∴∠ABD=∠DBC(_____________________________________)
∵ED∥BC(已知)
∴∠BDE=∠DBC(_________________________________)
∴∠ABD=∠BDE,
又∵∠FED=∠BDE(_____)
∴EF∥BD(_________________________________),
∴∠AEF=∠ABD(_________________________________)
∴∠AEF=∠FED(_________________________________),
∴EF是∠AED的平分线
17.已知:如图,.平分.
(1)求证:;
(2)求的度数.
18.如图,已知平分,求的度数.
19.(1)完成下面的证明.
如图,在四边形中,,是的平分线.求证:.
证明:是的平分线(已知)
__________________(角平分线的定义)
又(已知)
__________________(等量代换)
(____________________________)
(2)已知线段,是的中点,在直线上,且,画图并计算的长.
答案
一、单选题
B.B.A.B.C.C.B.B.
二、填空题
9.>
10.①②③④.
11.40°.
12.
13.120°
14.50.
三、解答题
15.
解:分别作的角平分线,如图,
∴交点P即为所求.
16.∵BD是∠ABC的平分线,
∴∠ABD=∠DBC(角平分线定义)
∵ED∥BC(已知)
∴∠BDE=∠DBC(两条直线平行,内错角相等)
∴∠ABD=∠BDE,
又∵∠FED=∠BDE(已知)
∴EF∥BD(内错角相等,两条直线平行),
∴∠AEF=∠ABD(两条直线平行,同位角相等)
∴∠AEF=∠FED(等量代换),
∴EF是∠AED的平分线
17.
解:(1)证明:,
,
;
(2)由(1)得
平分
18.
∵∠AOB=90°,∠BOC=40°,
∴∠AOC=90°+40°=130°,
∵OD平分∠AOC,
∴∠DOC=130°÷2=65°,
∴∠BOD=∠DOC-∠BOC=25°.
19.解:(1)平分(已知)
.(角平分线的定义)
(已知)
. (等量代换)
.(内错角相等,两直线平行)
故答案为1,3,2,3,内错角相等,两直线平行;
(2),是的中点
①当点D在线段AB上时,CD=CB-DB=6-2=4cm;
②当点D在线段AB的延长线上时,CD=CB+BD=6+2=8cm;
综上所述,CD的长为4cm或8cm.
20.
解:∵∠COD=116°,∠BOD=90°,
∴∠BOC=∠COD-∠BOD=116°-90°=26°,
∵OA平分∠BOC,
∴∠AOB=∠BOC÷2=13°,
∴∠AOD=∠BOD-∠AOB=90°+13°=103°
