八年级数学上册试题 12.2一次函数同步练习-沪科版(含答案)
文档属性
| 名称 | 八年级数学上册试题 12.2一次函数同步练习-沪科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 285.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 18:55:56 | ||
图片预览




文档简介
12.2一次函数
第一课时
一、单选题
1.已知y关于x成正比例,且当时,,则当时,y的值为
A.3 B. C.12 D.
2.已知函数y=(m+1)是正比例函数,且图象在第二、四象限内,则m的值是( )
A.2 B.﹣2 C.±2 D.
3.若b>0,则一次函数y=﹣x+b的图象大致是( )
A. B. C. D.
4.对于函数y=2x﹣1,下列说法正确的是( )
A.它的图象过点(1,0) B.y值随着x值增大而减小
C.它的图象经过第二象限 D.当x>1时,y>0
5.已知:将直线y=x﹣1向上平移2个单位长度后得到直线y=kx+b,则下列关于直线y=kx+b的说法正确的是( )
A.经过第一、二、四象限 B.与x轴交于(1,0)
C.与y轴交于(0,1) D.y随x的增大而减小
二、填空题
6.如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行,且经过点A(1,﹣2),则kb=__.
7.已知自变量为x的函数y=mx+2-m是正比例函数,则m=________,该函数的解析式为________.
8. 在平面直角坐标系中,已知一次函数y=x 1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1_____y2(填“>”,“<”或“=”)
9.已知函数y=(m﹣1)x+m2﹣1是正比例函数,则m=_____.
三、解答题
10.已知一次函数(k为常数,k≠0)和.
(1)当k=﹣2时,若>,求x的取值范围;
(2)当x<1时,>.结合图像,直接写出k的取值范围.
11.如图,一次函数y=kx+b的图象经过(2,4)、(0,2)两点,与x轴相交于点C.求:
(1)此一次函数的解析式;
(2)△AOC的面积.
12.声音在空气中的传播速度y(m/s)(秒音速)与气温x(℃)的关系,如下表.
(1)直接写出y与x间的关系式;
(2)当x=150 ℃时,音速y是多少?当音速为352 m/s时,气温x是多少?
13.如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴负半轴上,且满足S△COD=S△BOC,求点D的坐标.
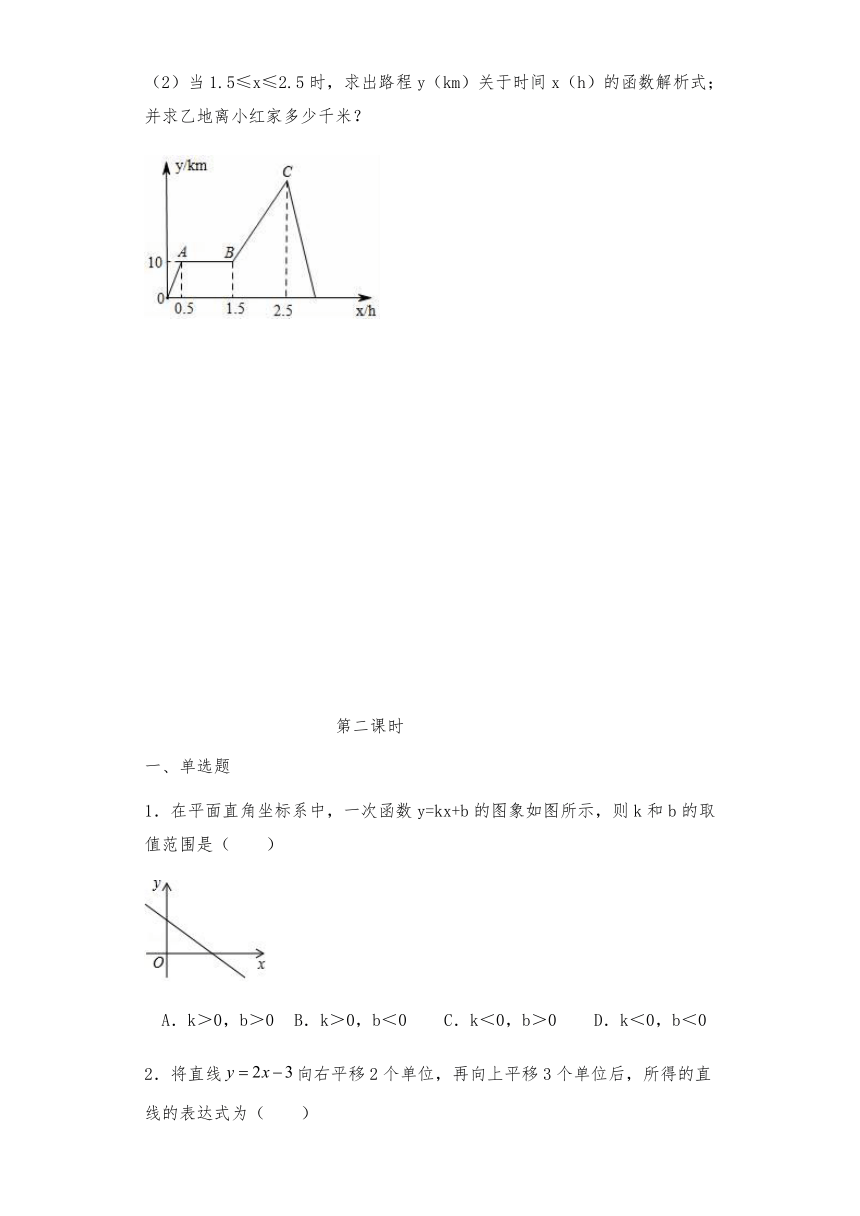
14.“低碳生活,绿色出行”的理念已深入人心,现在越来越多的人选择骑自行车上下班或外出旅游.周末,小红相约到郊外游玩,她从家出发0.5小时后到达甲地,玩一段时间后按原速前往乙地,刚到达乙地,接到妈妈电话,快速返回家中.小红从家出发到返回家中,行进路程y(km)随时间x(h)变化的函数图象大致如图所示.
(1)小红从甲地到乙地骑车的速度为 km/h;
(2)当1.5≤x≤2.5时,求出路程y(km)关于时间x(h)的函数解析式;并求乙地离小红家多少千米?
第二课时
一、单选题
1.在平面直角坐标系中,一次函数y=kx+b的图象如图所示,则k和b的取值范围是( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
2.将直线向右平移2个单位,再向上平移3个单位后,所得的直线的表达式为( )
A. B. C. D.
3.一次函数的图象经过原点,则k的值为
A.2 B. C.2或 D.3
4.如图,两个不同的一次函数y=ax+b与y=bx+a的图象在同一平面直角坐标系的位置可能是( )
A. B. C. D.
5.在平面直角坐标系中,过点(1,2)作直线l,若直线l与两坐标轴围成的三角形面积为4,则满足条件的直线l的条数是( )
A.5 B.4 C.3 D.2
二、填空题
6.若点M(k﹣1,k+1)关于y轴的对称点在第四象限内,则一次函数y=(k﹣1)x+k的图象不经过第 象限.
7.当直线经过第二、三、四象限时,则的取值范围是_____.
8.已知点A(x1, y1)、B(x2, y2)在直线y=kx+b上,且直线经过第一、二、四象限,当x1<x2时,y1与y2的大小关系为________.
9.甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步600米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则b=_____.
三、解答题
10.如图,直角坐标系xOy中,一次函数y=﹣x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,直接写出k的值.
11.如图,已知一次函数y=kx+b的图象经过A(﹣2,﹣1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
(1)求该一次函数的解析式;
(2)求△AOB的面积.
12.已知函数y=(m+1)x2-|m|+n+4.
(1)当m,n为何值时,此函数是一次函数?
(2)当m,n为何值时,此函数是正比例函数?
13.两个一次函数的图象如图所示,
(1)分别求出两个一次函数的解析式;
(2)求出两个一次函数图象的交点C坐标;
(3)求这两条直线与y轴围成△ABC的面积.
14.已知y与x成正比例函数,当x=1时,y=2.求:
(1)求y与x之间的函数关系式;
(2)求当x=-1时的函数值;
(3)如果当y的取值范围是0≤y≤5,求x的取值范围.
第一课时答案
一、单选题
B.B.C.D.C.
二、填空题
6.﹣8.
7.2; y=2x
8.<.
9.﹣1.
三、解答题
10.
解:(1)当时,.
根据题意,得.
解得.
(2)当x=1时,y=x 3= 2,
把(1, 2)代入y1=kx+2得k+2= 2,解得k= 4,
当 4≤k<0时,y1>y2;
当0<k≤1时,y1>y2.
∴k的取值范围是:且.
11.解:
(1)由图可知、,
,
解得,
故此一次函数的解析式为:;
(2)由图可知,
,,
,,
.
答:的面积是4.
12.
解:(1) 设y=kx+b(k≠0),
∵x=0时,y=331,x=5时,y=334,
∴
解得
∴y=x+331;
(2)当x=150时,y=0.6×150+331=421,
当y=352时,0.6x+331=352,
解得x=35.
答:当x=150℃时,音速y是421 m/s,
当音速为352 m/s时,气温x是35℃.
13.(1)当x=1时,y=3x=3,
∴点C的坐标为(1,3).
将A(﹣2,6)、C(1,3)代入y=kx+b,
得:,
解得:.
(2)当y=0时,有﹣x+4=0,
解得:x=4,
∴点B的坐标为(4,0).
设点D的坐标为(0,m)(m<0),
∵S△COD=S△BOC,即﹣m=××4×3,
解得:m=-4,
∴点D的坐标为(0,-4).
14.
(1)在OA段,速度==20km/h,
故答案为:20;
(2)当1.5≤x≤2.5时,设y=20x+b,把(1.5,10)代入得到,10=20×1.5+b,
解得b=﹣20,
∴y=20x﹣20,
当x=2.5时,解得y=30,
∴乙地离小红家30千米.
第二课时答案
一、单选题
C.A.A.C.C.
二、填空题
6.一
7..
8.y1>y2
9.192.
三、解答题
10.(1)把C(m,4)代入一次函数y=﹣x+5,可得
4=﹣m+5,
解得m=2,
∴C(2,4),
设l2的解析式为y=ax,则4=2a,
解得a=2,
∴l2的解析式为y=2x;
(2)如图,过C作CD⊥AO于D,CE⊥BO于E,则CD=4,CE=2,
y=﹣x+5,令x=0,则y=5;令y=0,则x=10,
∴A(10,0),B(0,5),
∴AO=10,BO=5,
∴S△AOC﹣S△BOC=×10×4﹣×5×2=20﹣5=15;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,
∴当l3经过点C(2,4)时,k=;
当l2,l3平行时,k=2;
当11,l3平行时,k=﹣;
故k的值为或2或﹣.
11.
解:(1)把A(﹣2,﹣1),B(1,3)代入y=kx+b得,
解得.所以一次函数解析式为y=x+;
(2)把x=0代入y=x+得y=,
所以D点坐标为(0,),
所以△AOB的面积=S△AOD+S△BOD=×y=x+;
×2+×y=x+×1=.
12.
(1)根据一次函数的定义,得:
2 |m|=1,
解得:m=±1.
又∵m+1≠0即m≠ 1,
∴当m=1,n为任意实数时,这个函数是一次函数;
(2)根据正比例函数的定义,得:
2 |m|=1,n+4=0,
解得:m=±1,n= 4,
又∵m+1≠0即m≠ 1,
∴当m=1,n= 4时,这个函数是正比例函数.
13.解:(1)设l1的解析式为y=k1x+b1,l2的解析式为y=k2x+b2,把(﹣2,0),(0,﹣3)代入l1,(4,0),(0,1)代入l2得, ,,
解得: ,.所以l1的解析式为y=﹣x﹣3,l2的解析式为y=﹣x+1;
(2)联立方程组 ,解得: ,所以两个一次函数图象的交点坐标(,);
(3)三角形的面积==.
14.
解:(1)设y=kx,将x=1、y=2代入,得:k=2,故y=2x;
(2)当x=-1时,y=2×(-1)=-2;
(3)∵,
∴,
解得:;
故答案是:(1) y=2x;(2)-2;(3).
第一课时
一、单选题
1.已知y关于x成正比例,且当时,,则当时,y的值为
A.3 B. C.12 D.
2.已知函数y=(m+1)是正比例函数,且图象在第二、四象限内,则m的值是( )
A.2 B.﹣2 C.±2 D.
3.若b>0,则一次函数y=﹣x+b的图象大致是( )
A. B. C. D.
4.对于函数y=2x﹣1,下列说法正确的是( )
A.它的图象过点(1,0) B.y值随着x值增大而减小
C.它的图象经过第二象限 D.当x>1时,y>0
5.已知:将直线y=x﹣1向上平移2个单位长度后得到直线y=kx+b,则下列关于直线y=kx+b的说法正确的是( )
A.经过第一、二、四象限 B.与x轴交于(1,0)
C.与y轴交于(0,1) D.y随x的增大而减小
二、填空题
6.如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行,且经过点A(1,﹣2),则kb=__.
7.已知自变量为x的函数y=mx+2-m是正比例函数,则m=________,该函数的解析式为________.
8. 在平面直角坐标系中,已知一次函数y=x 1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1_____y2(填“>”,“<”或“=”)
9.已知函数y=(m﹣1)x+m2﹣1是正比例函数,则m=_____.
三、解答题
10.已知一次函数(k为常数,k≠0)和.
(1)当k=﹣2时,若>,求x的取值范围;
(2)当x<1时,>.结合图像,直接写出k的取值范围.
11.如图,一次函数y=kx+b的图象经过(2,4)、(0,2)两点,与x轴相交于点C.求:
(1)此一次函数的解析式;
(2)△AOC的面积.
12.声音在空气中的传播速度y(m/s)(秒音速)与气温x(℃)的关系,如下表.
(1)直接写出y与x间的关系式;
(2)当x=150 ℃时,音速y是多少?当音速为352 m/s时,气温x是多少?
13.如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴负半轴上,且满足S△COD=S△BOC,求点D的坐标.
14.“低碳生活,绿色出行”的理念已深入人心,现在越来越多的人选择骑自行车上下班或外出旅游.周末,小红相约到郊外游玩,她从家出发0.5小时后到达甲地,玩一段时间后按原速前往乙地,刚到达乙地,接到妈妈电话,快速返回家中.小红从家出发到返回家中,行进路程y(km)随时间x(h)变化的函数图象大致如图所示.
(1)小红从甲地到乙地骑车的速度为 km/h;
(2)当1.5≤x≤2.5时,求出路程y(km)关于时间x(h)的函数解析式;并求乙地离小红家多少千米?
第二课时
一、单选题
1.在平面直角坐标系中,一次函数y=kx+b的图象如图所示,则k和b的取值范围是( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
2.将直线向右平移2个单位,再向上平移3个单位后,所得的直线的表达式为( )
A. B. C. D.
3.一次函数的图象经过原点,则k的值为
A.2 B. C.2或 D.3
4.如图,两个不同的一次函数y=ax+b与y=bx+a的图象在同一平面直角坐标系的位置可能是( )
A. B. C. D.
5.在平面直角坐标系中,过点(1,2)作直线l,若直线l与两坐标轴围成的三角形面积为4,则满足条件的直线l的条数是( )
A.5 B.4 C.3 D.2
二、填空题
6.若点M(k﹣1,k+1)关于y轴的对称点在第四象限内,则一次函数y=(k﹣1)x+k的图象不经过第 象限.
7.当直线经过第二、三、四象限时,则的取值范围是_____.
8.已知点A(x1, y1)、B(x2, y2)在直线y=kx+b上,且直线经过第一、二、四象限,当x1<x2时,y1与y2的大小关系为________.
9.甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步600米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则b=_____.
三、解答题
10.如图,直角坐标系xOy中,一次函数y=﹣x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,直接写出k的值.
11.如图,已知一次函数y=kx+b的图象经过A(﹣2,﹣1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
(1)求该一次函数的解析式;
(2)求△AOB的面积.
12.已知函数y=(m+1)x2-|m|+n+4.
(1)当m,n为何值时,此函数是一次函数?
(2)当m,n为何值时,此函数是正比例函数?
13.两个一次函数的图象如图所示,
(1)分别求出两个一次函数的解析式;
(2)求出两个一次函数图象的交点C坐标;
(3)求这两条直线与y轴围成△ABC的面积.
14.已知y与x成正比例函数,当x=1时,y=2.求:
(1)求y与x之间的函数关系式;
(2)求当x=-1时的函数值;
(3)如果当y的取值范围是0≤y≤5,求x的取值范围.
第一课时答案
一、单选题
B.B.C.D.C.
二、填空题
6.﹣8.
7.2; y=2x
8.<.
9.﹣1.
三、解答题
10.
解:(1)当时,.
根据题意,得.
解得.
(2)当x=1时,y=x 3= 2,
把(1, 2)代入y1=kx+2得k+2= 2,解得k= 4,
当 4≤k<0时,y1>y2;
当0<k≤1时,y1>y2.
∴k的取值范围是:且.
11.解:
(1)由图可知、,
,
解得,
故此一次函数的解析式为:;
(2)由图可知,
,,
,,
.
答:的面积是4.
12.
解:(1) 设y=kx+b(k≠0),
∵x=0时,y=331,x=5时,y=334,
∴
解得
∴y=x+331;
(2)当x=150时,y=0.6×150+331=421,
当y=352时,0.6x+331=352,
解得x=35.
答:当x=150℃时,音速y是421 m/s,
当音速为352 m/s时,气温x是35℃.
13.(1)当x=1时,y=3x=3,
∴点C的坐标为(1,3).
将A(﹣2,6)、C(1,3)代入y=kx+b,
得:,
解得:.
(2)当y=0时,有﹣x+4=0,
解得:x=4,
∴点B的坐标为(4,0).
设点D的坐标为(0,m)(m<0),
∵S△COD=S△BOC,即﹣m=××4×3,
解得:m=-4,
∴点D的坐标为(0,-4).
14.
(1)在OA段,速度==20km/h,
故答案为:20;
(2)当1.5≤x≤2.5时,设y=20x+b,把(1.5,10)代入得到,10=20×1.5+b,
解得b=﹣20,
∴y=20x﹣20,
当x=2.5时,解得y=30,
∴乙地离小红家30千米.
第二课时答案
一、单选题
C.A.A.C.C.
二、填空题
6.一
7..
8.y1>y2
9.192.
三、解答题
10.(1)把C(m,4)代入一次函数y=﹣x+5,可得
4=﹣m+5,
解得m=2,
∴C(2,4),
设l2的解析式为y=ax,则4=2a,
解得a=2,
∴l2的解析式为y=2x;
(2)如图,过C作CD⊥AO于D,CE⊥BO于E,则CD=4,CE=2,
y=﹣x+5,令x=0,则y=5;令y=0,则x=10,
∴A(10,0),B(0,5),
∴AO=10,BO=5,
∴S△AOC﹣S△BOC=×10×4﹣×5×2=20﹣5=15;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,
∴当l3经过点C(2,4)时,k=;
当l2,l3平行时,k=2;
当11,l3平行时,k=﹣;
故k的值为或2或﹣.
11.
解:(1)把A(﹣2,﹣1),B(1,3)代入y=kx+b得,
解得.所以一次函数解析式为y=x+;
(2)把x=0代入y=x+得y=,
所以D点坐标为(0,),
所以△AOB的面积=S△AOD+S△BOD=×y=x+;
×2+×y=x+×1=.
12.
(1)根据一次函数的定义,得:
2 |m|=1,
解得:m=±1.
又∵m+1≠0即m≠ 1,
∴当m=1,n为任意实数时,这个函数是一次函数;
(2)根据正比例函数的定义,得:
2 |m|=1,n+4=0,
解得:m=±1,n= 4,
又∵m+1≠0即m≠ 1,
∴当m=1,n= 4时,这个函数是正比例函数.
13.解:(1)设l1的解析式为y=k1x+b1,l2的解析式为y=k2x+b2,把(﹣2,0),(0,﹣3)代入l1,(4,0),(0,1)代入l2得, ,,
解得: ,.所以l1的解析式为y=﹣x﹣3,l2的解析式为y=﹣x+1;
(2)联立方程组 ,解得: ,所以两个一次函数图象的交点坐标(,);
(3)三角形的面积==.
14.
解:(1)设y=kx,将x=1、y=2代入,得:k=2,故y=2x;
(2)当x=-1时,y=2×(-1)=-2;
(3)∵,
∴,
解得:;
故答案是:(1) y=2x;(2)-2;(3).
