八年级数学上册试题 12.3一次函数与二元一次方程-沪科版(含答案)
文档属性
| 名称 | 八年级数学上册试题 12.3一次函数与二元一次方程-沪科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 454.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 18:57:04 | ||
图片预览



文档简介
12.3一次函数与二元一次方程
第一课时
一、单选题
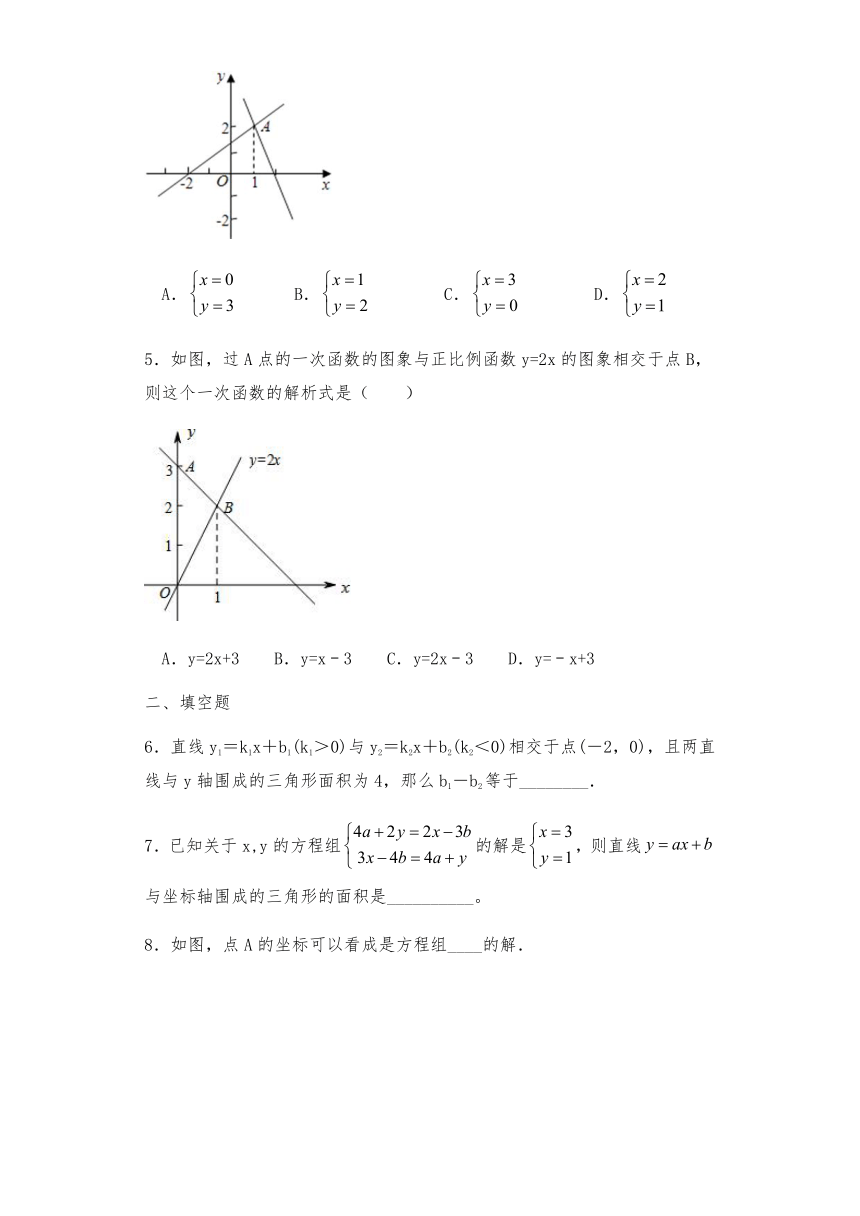
1.用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图所示),则所解的二元一次方程组是 ( )
A. B.
C. D.
2.直线y=-2x+m与直线y=2x-1的交点在第四象限,则m的取值范围是( )
A.m>-1 B.m<1 C.-1<m<1 D.-1≤m≤1
3.已知一次函数和的图象都经过点A,且分别交轴于B、C两点 那么的面积是
A.3 B.4 C.5 D.6
4.已知一次函数y=kx+b和y=x+a的图象交于点A,则关于x,y的二元一次方程组的解为( )
A. B. C. D.
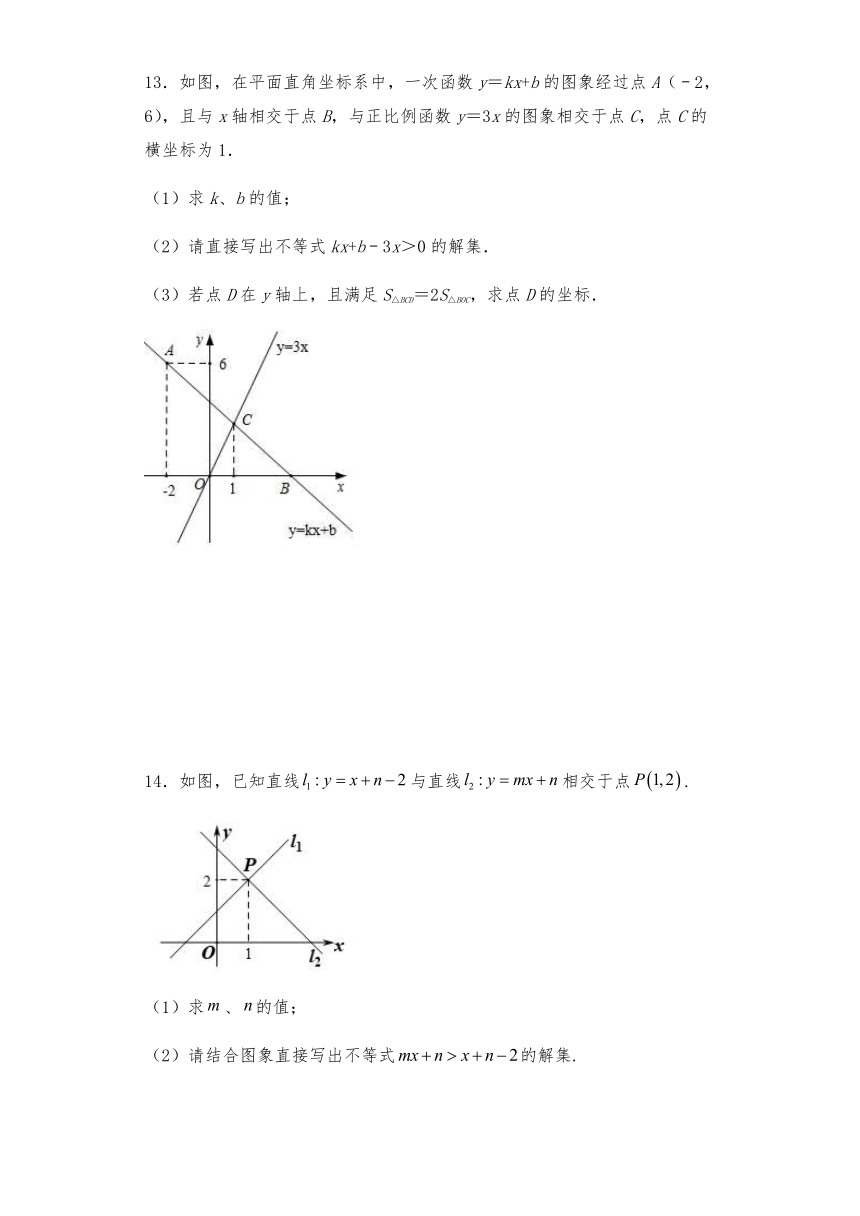
5.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是( )
A.y=2x+3 B.y=x﹣3 C.y=2x﹣3 D.y=﹣x+3
二、填空题
6.直线y1=k1x+b1(k1>0)与y2=k2x+b2(k2<0)相交于点(-2,0),且两直线与y轴围成的三角形面积为4,那么b1-b2等于________.
7.已知关于x,y的方程组的解是,则直线与坐标轴围成的三角形的面积是__________。
8.如图,点A的坐标可以看成是方程组____的解.
9.如果直线 y=-2x+k 与两坐标轴所围成的三角形面积是 9,则 k的值为_____.
三、解答题
10.如图,直线的函数解析式为,且与轴交于点,直线经过点、,直线、交于点.
(1)求直线的函数解析式;
(2)求的面积;
(3)在直线上是否存在点,使得面积是面积的倍?如果存在,请求出坐标;如果不存在,请说明理由.
11.已知直线y=kx+b(k≠0)经过点A(3,0),B(1,2)
(1)求直线y=kx+b的函数表达式;
(2)若直线y=x﹣2与直线y=kx+b相交于点C,求点C的坐标;
(3)写出不等式kx+b>x﹣2的解.
12.如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b)
(1)求b,m的值
(2)垂直于x轴的直线x=a与直线l1,l2分别相交于C,D,若线段CD长为2,求a的值
13.如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)请直接写出不等式kx+b﹣3x>0的解集.
(3)若点D在y轴上,且满足S△BCD=2S△BOC,求点D的坐标.
14.如图,已知直线与直线相交于点.
(1)求、的值;
(2)请结合图象直接写出不等式的解集.
第二课时
一、单选题
1.若以二元一次方程x+2y﹣b=0的解为坐标的点(x,y)都在直线y=﹣x+b﹣l上,则常数b=( )
A. B.2 C.﹣1 D.1
2.若直线l1经过点(0,4),l2经过(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为
A.(-2,0) B.(2,0) C.(-6,0) D.(6,0)
3.把直线向上平移m个单位后,与直线的交点在第一象限,则m的取值范围是( )
A.1<m<7 B.3<m<4 C.m>1 D.m<4
4.某二元方程的解是(为实数),若把看作平面直角坐标系中点的横坐标,看作平面直角坐标系中点的纵坐标,下面说法正确的是( )
A.点一定不在第一象限 B.点一定不在第二象限
C.随的增大而增大 D.点一定不在第三象限
5.定义,当时,,当<时,;已知函数,则该函数的最大值是
A. B. C. D.
二、填空题
6.如图,一次函数y=ax+b的图象经过A、B两点,则关于x的不等式的解集是______________.
7.作出函数y=﹣x+3的图象,并利用图象回答问题:
(1)当y<0时,x的取值范围为_____;
(2)当﹣2<x<2时,y的取值范围为_____;
(3)图象与直线y=x﹣1的交点坐标为______;这两条直线与y轴围成的三角形面积为______.
8.利用如图所示的函数图象回答下列问题:
(1)方程组的解为________;
(2)不等式2x>-x+3的解集为________.
9.直线y=-2x+m+2和直线y=3x+m-3的交点坐标互为相反数,则m=______。
三、解答题
10.直线n与过原点的直线m交于点P,P点的坐标如图所示,直线n与y轴交于点A;若OA=OP;
(1)求A点的坐标;
(2)求直线m,n的函数表达式;
(3)求△AOP的面积.
11.已知一次函数 y=kx+b 的图象经过点(-1,-5),且与正比例函数于点(2,a),求:
(1)a 的值;
(2)k,b 的值;
(3)这两个函数图象与 x 轴所围成的三角形的面积.
12.在平面直角坐标系xOy中,直线与y轴交于点A.
(1)如图,直线与直线交于点B,与y轴交于点C,点B横坐标为.
①求点B的坐标及k的值;
②直线与直线与y轴所围成的△ABC的面积等于 ;
(2)直线与x轴交于点E(,0),若,求k的取值范围.
13.如图,一次函数的图象经过点,且与x轴相交于点B,与正比例函数的图象相交于点C,点C的横坐标为1.
(1)求一次函数的表达式;
(2)若点D在y轴负半轴上,且满足,求点D的坐标.
14.在平面直角坐标系中有两条直线:和,它们的交点为点P,且它们与轴的交点分别为A、B.
(1)在同一坐标系中作出两条直线的图象;
(2)求A、B两点的坐标和△PAB的面积.
第二课时答案
一、单选题
D.C.D.B.D.
二、填空题
6.4
7.4.
8.
9.(±6.
三、解答题
10.
解:(1)设直线的函数解析式为,
将、代入,
,解得:,
直线的函数解析式为.
(2)联立两直线解析式成方程组,
,解得:,
点的坐标为.
当时,,
点的坐标为.
.
(3)假设存在.
面积是面积的倍,
,
当时,,
此时点的坐标为;
当时,,
此时点的坐标为.
综上所述:在直线上存在点或,使得面积是面积的倍.
故答案为(1);(2)3;(3)在直线上存在点或,使得面积是面积的倍.
11.
解:(1)根据题意得,解得,
∴直线解析式为y=﹣x+3;
(2)解方程组得,
∴C点坐标为(,);
(3)解不等式﹣x+3>x﹣2得x<,
即不等式kx+b>x﹣2的解集为x<.
12.
(1)∵点P(1,b)在直线l1:y=2x+1上,∴b=2×1+1=3;
∵点P(1,3)在直线l2:y=mx+4上,∴3=m+4,∴m=﹣1.
(2)当x=a时,yC=2a+1;
当x=a时,yD=4﹣a.
∵CD=2,∴|2a+1﹣(4﹣a)|=2,解得:a=或a=,∴a=或a=.
13.
解:(1)当x=1时,y=3x=3,
∴点C的坐标为(1,3).
将A(﹣2,6)、C(1,3)代入y=kx+b,
得:
解得:;
(2)由kx+b﹣3x>0,得
kx+b>3x,
∵点C的横坐标为1,
∴x<1;
(3)由(1)直线AB:y=﹣x+4
当y=0时,有﹣x+4=0,
解得:x=4,
∴点B的坐标为(4,0).
设点D的坐标为(0,m),
∴直线DB:y=-,
过点C作CE∥y轴,交BD于点E,则E(1,),
∴CE=|3﹣ |
∴S△BCD=S△CED+S△CEB== |3﹣ |×4=2|3﹣ |.
∵S△BCD=2S△BOC,即2|3﹣ |=×4×3×2,
解得:m=﹣4或12,
∴点D的坐标为D(0,﹣4)或D(0,12).
14.
解:(1)因为点P是两条直线的交点,所以把点分别代入与中,得,,解得,.
(2)当时,的图象在的上面,
所以,不等式的解集是.
第二课时答案
一、单选题
B.B.C.A.B.
二、填空题
6.x<2
7.(1) x>3;(2) 1<y<5;(3)(2,1);4.
8.(1);(2)x>1.
9.-1.
三、解答题
10.
解:(1)∵点P的坐标为(4,3),
∴OP==5,
∵OA=OP,
∴点A的坐标为(0,-5);
(2)设直线n的解析式为y1=kx+b,直线m的解析式为y2=ax,
把A、P点坐标代入直线n,可得:,
解得:,
把O、P点坐标代入直线m,可得:3=4a,
解得:a=,
所以直线m,n的函数表达式分别为:y=x、y=2x-5;
(3)△AOP的面积=×5×3=.
11.
(1)由题知,把(2,a)代入y=x,解得a=1;
(2)由题意知,把点(-1,-5)及点(2,a)代入一次函数解析式,
得:,
又由(1)知a=1,
解方程组得到:k=2,b=-3;
(3)由(2)知一次函数解析式为:y=2x-3,
y=2x-3与x轴交点坐标为(,0)
∴所求三角形面积S=×1×=.
12.
解:(1)①∵直线y=-2x+1过点B,点B的横坐标为-1,∴y=2+2=3.
∴B(-1,3).
∵直线y=kx+4过B点,
∴3=-k+4,解得:k=1.
②∵k=1,∴一次函数解析式为:y=x+4.
∴A(0,4).
∵y=-2x+1,∴C(0,1).∴AC=4-1=3.
∴△ABC的面积为:×1×3=.
(2)∵直线y=kx+4(k≠0)与x轴交于点E(x0,0),,
∴当x0=-2,则E(-2,0),代入y=kx+4得:0=-2k+4,解得:k=2.
当x0=-1,则E(-1,0),代入y=kx+4得:0=-k+4,解得:k=4.
∴k的取值范围是:2<k<4.
13.(1)当时,,
点C的坐标为.
将、代入,
得:,
解得:,
一次函数的表达式为:;
(2)当时,有,
解得:,
点B的坐标为.
设点D的坐标为,
,即,
解得:,
点D的坐标为.
14.(1)
,令y=0,知,x=-3, A(-3,0),
, y=0,, x=4, B(4,0),联立方程组
,解得,
所以△PAB面积是.
第一课时
一、单选题
1.用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图所示),则所解的二元一次方程组是 ( )
A. B.
C. D.
2.直线y=-2x+m与直线y=2x-1的交点在第四象限,则m的取值范围是( )
A.m>-1 B.m<1 C.-1<m<1 D.-1≤m≤1
3.已知一次函数和的图象都经过点A,且分别交轴于B、C两点 那么的面积是
A.3 B.4 C.5 D.6
4.已知一次函数y=kx+b和y=x+a的图象交于点A,则关于x,y的二元一次方程组的解为( )
A. B. C. D.
5.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是( )
A.y=2x+3 B.y=x﹣3 C.y=2x﹣3 D.y=﹣x+3
二、填空题
6.直线y1=k1x+b1(k1>0)与y2=k2x+b2(k2<0)相交于点(-2,0),且两直线与y轴围成的三角形面积为4,那么b1-b2等于________.
7.已知关于x,y的方程组的解是,则直线与坐标轴围成的三角形的面积是__________。
8.如图,点A的坐标可以看成是方程组____的解.
9.如果直线 y=-2x+k 与两坐标轴所围成的三角形面积是 9,则 k的值为_____.
三、解答题
10.如图,直线的函数解析式为,且与轴交于点,直线经过点、,直线、交于点.
(1)求直线的函数解析式;
(2)求的面积;
(3)在直线上是否存在点,使得面积是面积的倍?如果存在,请求出坐标;如果不存在,请说明理由.
11.已知直线y=kx+b(k≠0)经过点A(3,0),B(1,2)
(1)求直线y=kx+b的函数表达式;
(2)若直线y=x﹣2与直线y=kx+b相交于点C,求点C的坐标;
(3)写出不等式kx+b>x﹣2的解.
12.如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b)
(1)求b,m的值
(2)垂直于x轴的直线x=a与直线l1,l2分别相交于C,D,若线段CD长为2,求a的值
13.如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)请直接写出不等式kx+b﹣3x>0的解集.
(3)若点D在y轴上,且满足S△BCD=2S△BOC,求点D的坐标.
14.如图,已知直线与直线相交于点.
(1)求、的值;
(2)请结合图象直接写出不等式的解集.
第二课时
一、单选题
1.若以二元一次方程x+2y﹣b=0的解为坐标的点(x,y)都在直线y=﹣x+b﹣l上,则常数b=( )
A. B.2 C.﹣1 D.1
2.若直线l1经过点(0,4),l2经过(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为
A.(-2,0) B.(2,0) C.(-6,0) D.(6,0)
3.把直线向上平移m个单位后,与直线的交点在第一象限,则m的取值范围是( )
A.1<m<7 B.3<m<4 C.m>1 D.m<4
4.某二元方程的解是(为实数),若把看作平面直角坐标系中点的横坐标,看作平面直角坐标系中点的纵坐标,下面说法正确的是( )
A.点一定不在第一象限 B.点一定不在第二象限
C.随的增大而增大 D.点一定不在第三象限
5.定义,当时,,当<时,;已知函数,则该函数的最大值是
A. B. C. D.
二、填空题
6.如图,一次函数y=ax+b的图象经过A、B两点,则关于x的不等式的解集是______________.
7.作出函数y=﹣x+3的图象,并利用图象回答问题:
(1)当y<0时,x的取值范围为_____;
(2)当﹣2<x<2时,y的取值范围为_____;
(3)图象与直线y=x﹣1的交点坐标为______;这两条直线与y轴围成的三角形面积为______.
8.利用如图所示的函数图象回答下列问题:
(1)方程组的解为________;
(2)不等式2x>-x+3的解集为________.
9.直线y=-2x+m+2和直线y=3x+m-3的交点坐标互为相反数,则m=______。
三、解答题
10.直线n与过原点的直线m交于点P,P点的坐标如图所示,直线n与y轴交于点A;若OA=OP;
(1)求A点的坐标;
(2)求直线m,n的函数表达式;
(3)求△AOP的面积.
11.已知一次函数 y=kx+b 的图象经过点(-1,-5),且与正比例函数于点(2,a),求:
(1)a 的值;
(2)k,b 的值;
(3)这两个函数图象与 x 轴所围成的三角形的面积.
12.在平面直角坐标系xOy中,直线与y轴交于点A.
(1)如图,直线与直线交于点B,与y轴交于点C,点B横坐标为.
①求点B的坐标及k的值;
②直线与直线与y轴所围成的△ABC的面积等于 ;
(2)直线与x轴交于点E(,0),若,求k的取值范围.
13.如图,一次函数的图象经过点,且与x轴相交于点B,与正比例函数的图象相交于点C,点C的横坐标为1.
(1)求一次函数的表达式;
(2)若点D在y轴负半轴上,且满足,求点D的坐标.
14.在平面直角坐标系中有两条直线:和,它们的交点为点P,且它们与轴的交点分别为A、B.
(1)在同一坐标系中作出两条直线的图象;
(2)求A、B两点的坐标和△PAB的面积.
第二课时答案
一、单选题
D.C.D.B.D.
二、填空题
6.4
7.4.
8.
9.(±6.
三、解答题
10.
解:(1)设直线的函数解析式为,
将、代入,
,解得:,
直线的函数解析式为.
(2)联立两直线解析式成方程组,
,解得:,
点的坐标为.
当时,,
点的坐标为.
.
(3)假设存在.
面积是面积的倍,
,
当时,,
此时点的坐标为;
当时,,
此时点的坐标为.
综上所述:在直线上存在点或,使得面积是面积的倍.
故答案为(1);(2)3;(3)在直线上存在点或,使得面积是面积的倍.
11.
解:(1)根据题意得,解得,
∴直线解析式为y=﹣x+3;
(2)解方程组得,
∴C点坐标为(,);
(3)解不等式﹣x+3>x﹣2得x<,
即不等式kx+b>x﹣2的解集为x<.
12.
(1)∵点P(1,b)在直线l1:y=2x+1上,∴b=2×1+1=3;
∵点P(1,3)在直线l2:y=mx+4上,∴3=m+4,∴m=﹣1.
(2)当x=a时,yC=2a+1;
当x=a时,yD=4﹣a.
∵CD=2,∴|2a+1﹣(4﹣a)|=2,解得:a=或a=,∴a=或a=.
13.
解:(1)当x=1时,y=3x=3,
∴点C的坐标为(1,3).
将A(﹣2,6)、C(1,3)代入y=kx+b,
得:
解得:;
(2)由kx+b﹣3x>0,得
kx+b>3x,
∵点C的横坐标为1,
∴x<1;
(3)由(1)直线AB:y=﹣x+4
当y=0时,有﹣x+4=0,
解得:x=4,
∴点B的坐标为(4,0).
设点D的坐标为(0,m),
∴直线DB:y=-,
过点C作CE∥y轴,交BD于点E,则E(1,),
∴CE=|3﹣ |
∴S△BCD=S△CED+S△CEB== |3﹣ |×4=2|3﹣ |.
∵S△BCD=2S△BOC,即2|3﹣ |=×4×3×2,
解得:m=﹣4或12,
∴点D的坐标为D(0,﹣4)或D(0,12).
14.
解:(1)因为点P是两条直线的交点,所以把点分别代入与中,得,,解得,.
(2)当时,的图象在的上面,
所以,不等式的解集是.
第二课时答案
一、单选题
B.B.C.A.B.
二、填空题
6.x<2
7.(1) x>3;(2) 1<y<5;(3)(2,1);4.
8.(1);(2)x>1.
9.-1.
三、解答题
10.
解:(1)∵点P的坐标为(4,3),
∴OP==5,
∵OA=OP,
∴点A的坐标为(0,-5);
(2)设直线n的解析式为y1=kx+b,直线m的解析式为y2=ax,
把A、P点坐标代入直线n,可得:,
解得:,
把O、P点坐标代入直线m,可得:3=4a,
解得:a=,
所以直线m,n的函数表达式分别为:y=x、y=2x-5;
(3)△AOP的面积=×5×3=.
11.
(1)由题知,把(2,a)代入y=x,解得a=1;
(2)由题意知,把点(-1,-5)及点(2,a)代入一次函数解析式,
得:,
又由(1)知a=1,
解方程组得到:k=2,b=-3;
(3)由(2)知一次函数解析式为:y=2x-3,
y=2x-3与x轴交点坐标为(,0)
∴所求三角形面积S=×1×=.
12.
解:(1)①∵直线y=-2x+1过点B,点B的横坐标为-1,∴y=2+2=3.
∴B(-1,3).
∵直线y=kx+4过B点,
∴3=-k+4,解得:k=1.
②∵k=1,∴一次函数解析式为:y=x+4.
∴A(0,4).
∵y=-2x+1,∴C(0,1).∴AC=4-1=3.
∴△ABC的面积为:×1×3=.
(2)∵直线y=kx+4(k≠0)与x轴交于点E(x0,0),,
∴当x0=-2,则E(-2,0),代入y=kx+4得:0=-2k+4,解得:k=2.
当x0=-1,则E(-1,0),代入y=kx+4得:0=-k+4,解得:k=4.
∴k的取值范围是:2<k<4.
13.(1)当时,,
点C的坐标为.
将、代入,
得:,
解得:,
一次函数的表达式为:;
(2)当时,有,
解得:,
点B的坐标为.
设点D的坐标为,
,即,
解得:,
点D的坐标为.
14.(1)
,令y=0,知,x=-3, A(-3,0),
, y=0,, x=4, B(4,0),联立方程组
,解得,
所以△PAB面积是.
