八年级数学上册试题 14.2.2三边分别相等的两个三角形-沪科版(含答案)
文档属性
| 名称 | 八年级数学上册试题 14.2.2三边分别相等的两个三角形-沪科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 285.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 18:58:55 | ||
图片预览

文档简介
14.2.2三边分别相等的两个三角形
一、单选题
1.如图,在△ABC中,点D、F分别在边BC、AC上,若BC=ED,AC=CD,AB=CE,且∠ACE=180°-∠ABC-2m,对下列角中,大小为m的角是( )
A.∠CDF B.∠ABC C.∠CFD D.∠CFE
2.利用直尺和圆规作一个角等于已知角,作图如图,请你根据所学的三角形全等的有关知识,说明画出∠A′O′B′=∠AOB 的依据是( )
A.SAS B.ASA C.AAS D.SSS
3.下列条件中,不能判断的是( )
A. B.
C. D.
4.如图所示,点A,D,C,F在同一条直线上,AB=DE,AD=CF,要使△ABC≌△DEF,依据“SSS”还需要添加一个条件是( )
A.AD=CD B.BC=EF C.BC∥EF D.DC=CF
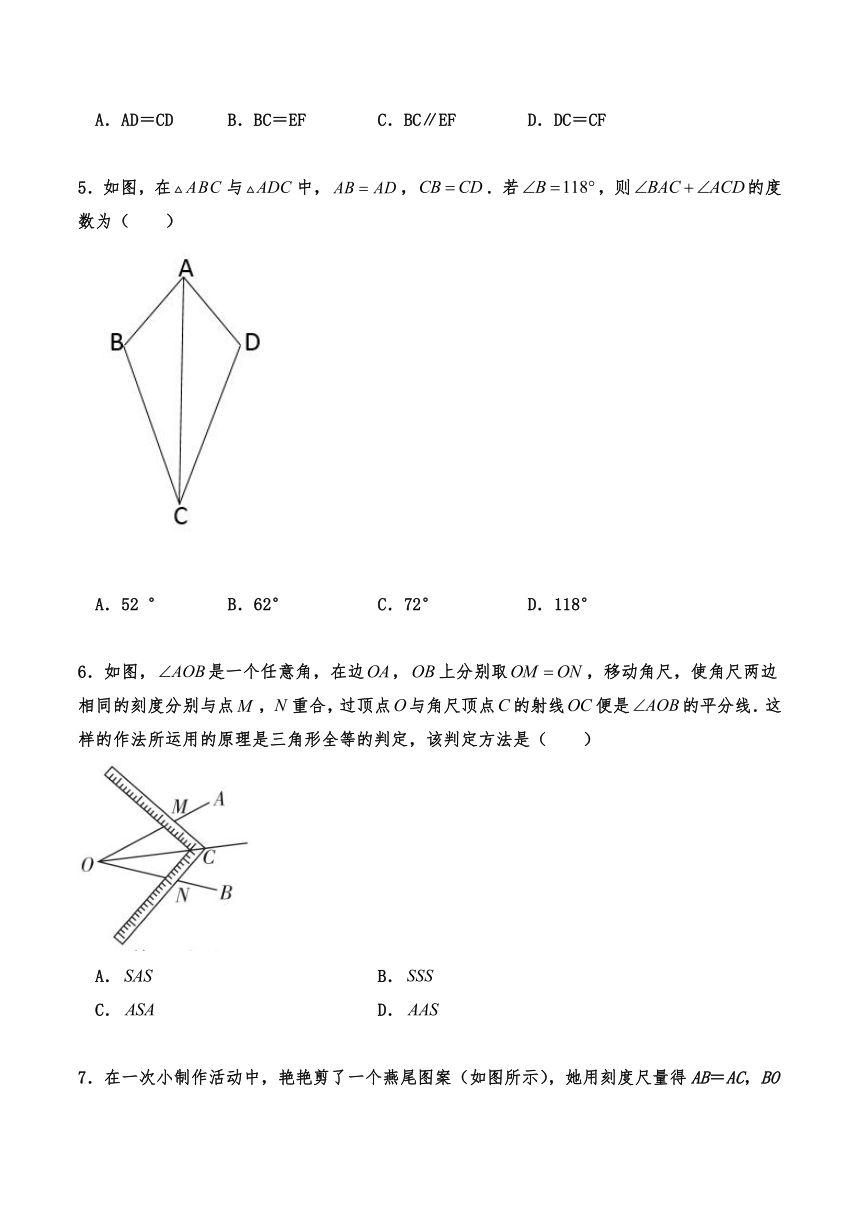
5.如图,在与中,,.若,则的度数为( )
A.52 ° B.62° C.72° D.118°
6.如图,是一个任意角,在边,上分别取,移动角尺,使角尺两边相同的刻度分别与点,重合,过顶点与角尺顶点的射线便是的平分线.这样的作法所运用的原理是三角形全等的判定,该判定方法是( )
A. B.
C. D.
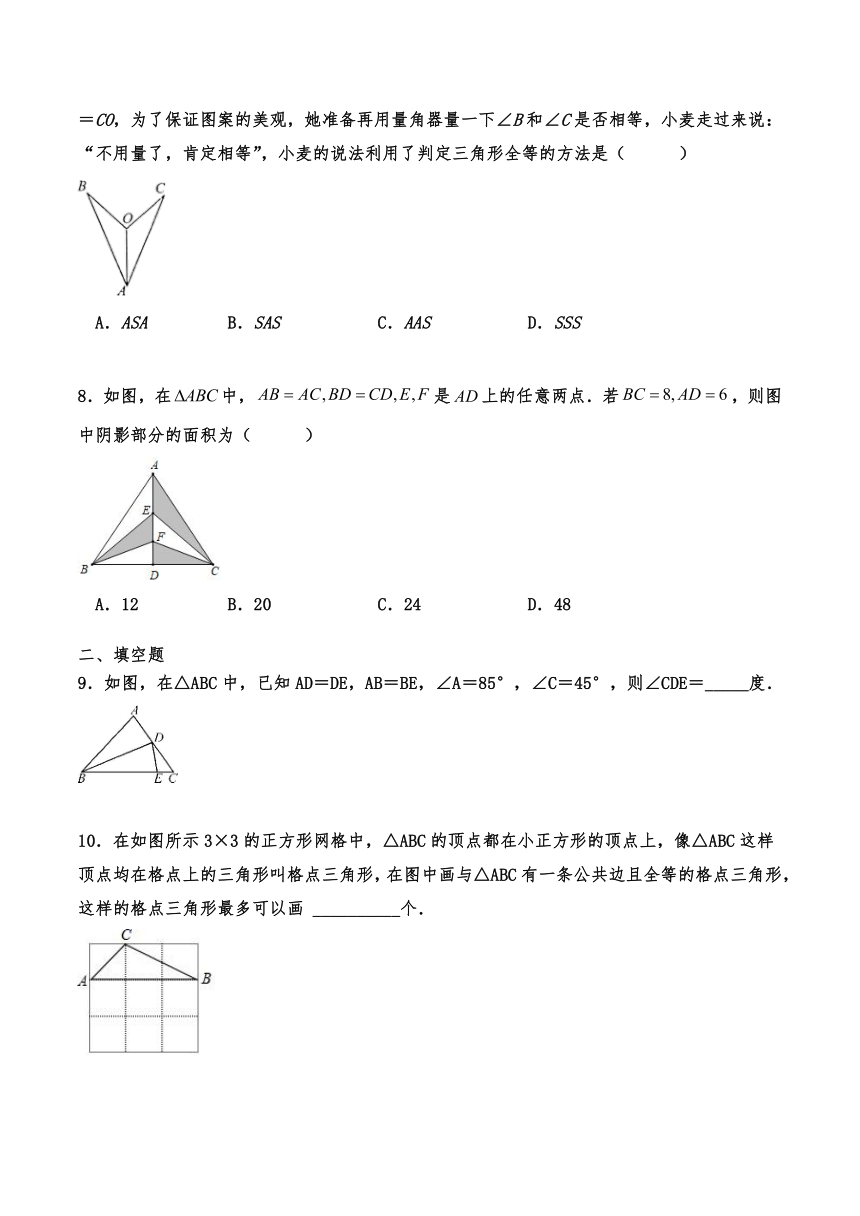
7.在一次小制作活动中,艳艳剪了一个燕尾图案(如图所示),她用刻度尺量得AB=AC,BO=CO,为了保证图案的美观,她准备再用量角器量一下∠B和∠C是否相等,小麦走过来说:“不用量了,肯定相等”,小麦的说法利用了判定三角形全等的方法是( )
A.ASA B.SAS C.AAS D.SSS
8.如图,在中,是上的任意两点.若,则图中阴影部分的面积为( )
A.12 B.20 C.24 D.48
二、填空题
9.如图,在△ABC中,已知AD=DE,AB=BE,∠A=85°,∠C=45°,则∠CDE=_____度.
10.在如图所示3×3的正方形网格中,△ABC的顶点都在小正方形的顶点上,像△ABC这样顶点均在格点上的三角形叫格点三角形,在图中画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画 __________个.
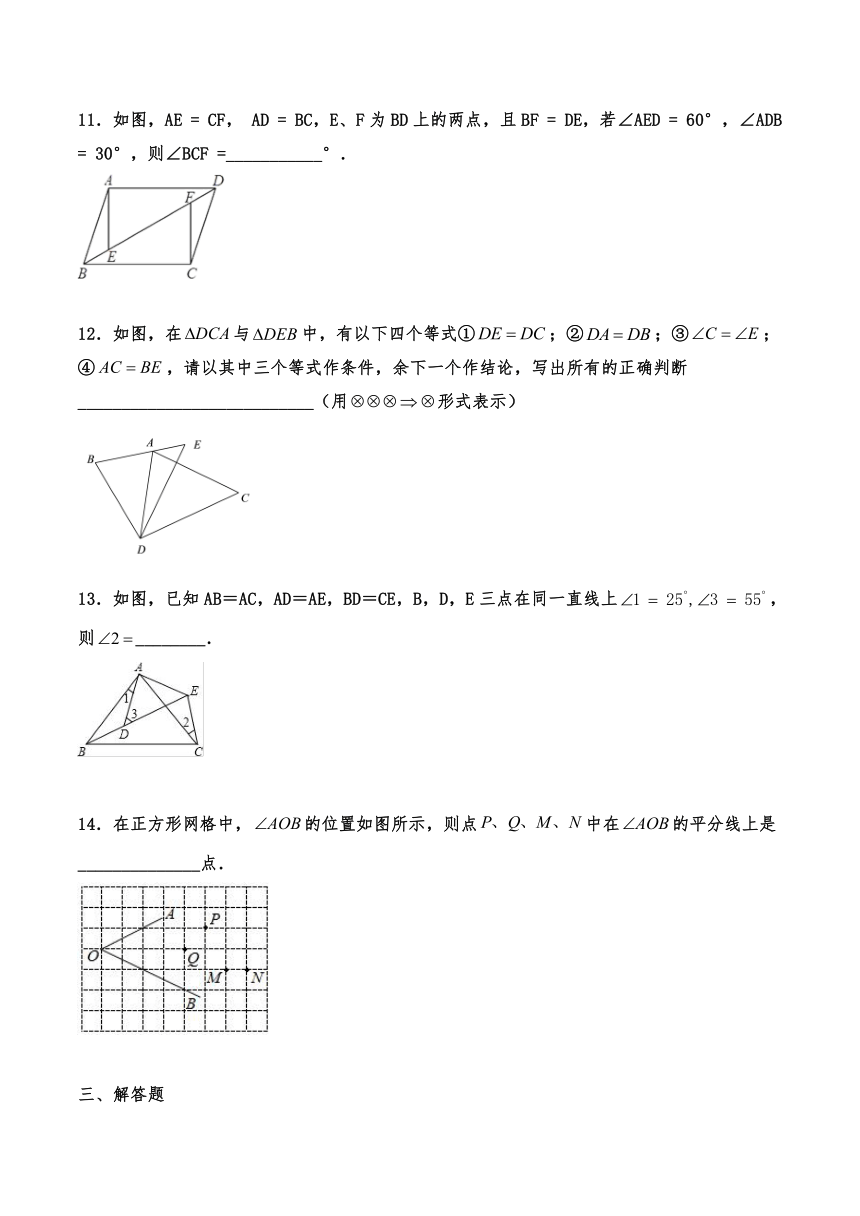
11.如图,AE = CF, AD = BC,E、F为BD上的两点,且BF = DE,若∠AED = 60°,∠ADB = 30°,则∠BCF =___________°.
12.如图,在与中,有以下四个等式①;②;③;④,请以其中三个等式作条件,余下一个作结论,写出所有的正确判断 ___________________________(用形式表示)
13.如图,已知AB=AC,AD=AE,BD=CE,B,D,E三点在同一直线上,则________.
14.在正方形网格中,的位置如图所示,则点中在的平分线上是______________点.
三、解答题
15.如图,点A、B、C、D在同一直线上,AM=CN,BM=DN,AC=BD.求证:BM//DN.
16.如图,AB=AD,BC=DC,求证:∠ABC=∠ADC.
17.如图,三角形钢架中,,AD是连接A与BC中点D的支架,
求证:.
18.“三月三,放风筝”如图是小颖制作的风筝,他根据 AD=BD,AC=BC,不用度量,就知道∠DAC=∠DBC,请你运用所学的知识,给予说明.
19.如图,点、、、在同一直线上,,,.
20.农科所有一块五边形的试验田如图所示,已知在五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=20 m,求这块试验田的面积.
答案
一、单选题
A.D.B.B.B.B.D.A.
二、填空题
9.40
10.4个.
11.90゜.
12.①②④ ③,①④③ ②.
13.30°.
14.Q.
三、解答题
15.
证明:∵AC=BD,
∴AC+BC=BD+BC,
即AB=CD,
∵在△ABM和△CDN中,
∴△ABM≌△CDN(SSS),
∴∠MBA=∠D,
∴BM∥DN.
16.
如图所示:
在△ABC与△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠ABC=∠ADC.
17.
证明:∵D是BC中点
∴BD=CD,
在△ABD和△ACD中 ,
∴△ABD≌△ACD(SSS).
18.
解:如图:连接CD,
在△ACD与△BCD中, ,
∴△ACD≌△BCD(SSS),
∴∠DAC=∠DBC.
19.
证明:(1)∵BE=CF,
∴BE+EC=CF+EC,即BC=EF,
∴在△ABC和△DEF中,,
∴△ABC≌△DEF(SSS)
(2)由(1)知△ABC≌△DEF,
∴∠ACB=∠F,
∴∠EGC=180°-∠GEC-∠GCE=180°-∠GEC-∠F=∠D .
20.如图,延长DE至点F,使EF=BC,连接AC,AD,AF.易得CD=FD.
因为
所以△ABC≌△AEF(SAS).
所以AC=AF.
在△ACD与△AFD中,因为
所以△ACD≌△AFD(SSS).
所以五边形ABCDE的面积是
2S△ADF=2×·DF·AE=2××20×20=400(m2).
一、单选题
1.如图,在△ABC中,点D、F分别在边BC、AC上,若BC=ED,AC=CD,AB=CE,且∠ACE=180°-∠ABC-2m,对下列角中,大小为m的角是( )
A.∠CDF B.∠ABC C.∠CFD D.∠CFE
2.利用直尺和圆规作一个角等于已知角,作图如图,请你根据所学的三角形全等的有关知识,说明画出∠A′O′B′=∠AOB 的依据是( )
A.SAS B.ASA C.AAS D.SSS
3.下列条件中,不能判断的是( )
A. B.
C. D.
4.如图所示,点A,D,C,F在同一条直线上,AB=DE,AD=CF,要使△ABC≌△DEF,依据“SSS”还需要添加一个条件是( )
A.AD=CD B.BC=EF C.BC∥EF D.DC=CF
5.如图,在与中,,.若,则的度数为( )
A.52 ° B.62° C.72° D.118°
6.如图,是一个任意角,在边,上分别取,移动角尺,使角尺两边相同的刻度分别与点,重合,过顶点与角尺顶点的射线便是的平分线.这样的作法所运用的原理是三角形全等的判定,该判定方法是( )
A. B.
C. D.
7.在一次小制作活动中,艳艳剪了一个燕尾图案(如图所示),她用刻度尺量得AB=AC,BO=CO,为了保证图案的美观,她准备再用量角器量一下∠B和∠C是否相等,小麦走过来说:“不用量了,肯定相等”,小麦的说法利用了判定三角形全等的方法是( )
A.ASA B.SAS C.AAS D.SSS
8.如图,在中,是上的任意两点.若,则图中阴影部分的面积为( )
A.12 B.20 C.24 D.48
二、填空题
9.如图,在△ABC中,已知AD=DE,AB=BE,∠A=85°,∠C=45°,则∠CDE=_____度.
10.在如图所示3×3的正方形网格中,△ABC的顶点都在小正方形的顶点上,像△ABC这样顶点均在格点上的三角形叫格点三角形,在图中画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画 __________个.
11.如图,AE = CF, AD = BC,E、F为BD上的两点,且BF = DE,若∠AED = 60°,∠ADB = 30°,则∠BCF =___________°.
12.如图,在与中,有以下四个等式①;②;③;④,请以其中三个等式作条件,余下一个作结论,写出所有的正确判断 ___________________________(用形式表示)
13.如图,已知AB=AC,AD=AE,BD=CE,B,D,E三点在同一直线上,则________.
14.在正方形网格中,的位置如图所示,则点中在的平分线上是______________点.
三、解答题
15.如图,点A、B、C、D在同一直线上,AM=CN,BM=DN,AC=BD.求证:BM//DN.
16.如图,AB=AD,BC=DC,求证:∠ABC=∠ADC.
17.如图,三角形钢架中,,AD是连接A与BC中点D的支架,
求证:.
18.“三月三,放风筝”如图是小颖制作的风筝,他根据 AD=BD,AC=BC,不用度量,就知道∠DAC=∠DBC,请你运用所学的知识,给予说明.
19.如图,点、、、在同一直线上,,,.
20.农科所有一块五边形的试验田如图所示,已知在五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=20 m,求这块试验田的面积.
答案
一、单选题
A.D.B.B.B.B.D.A.
二、填空题
9.40
10.4个.
11.90゜.
12.①②④ ③,①④③ ②.
13.30°.
14.Q.
三、解答题
15.
证明:∵AC=BD,
∴AC+BC=BD+BC,
即AB=CD,
∵在△ABM和△CDN中,
∴△ABM≌△CDN(SSS),
∴∠MBA=∠D,
∴BM∥DN.
16.
如图所示:
在△ABC与△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠ABC=∠ADC.
17.
证明:∵D是BC中点
∴BD=CD,
在△ABD和△ACD中 ,
∴△ABD≌△ACD(SSS).
18.
解:如图:连接CD,
在△ACD与△BCD中, ,
∴△ACD≌△BCD(SSS),
∴∠DAC=∠DBC.
19.
证明:(1)∵BE=CF,
∴BE+EC=CF+EC,即BC=EF,
∴在△ABC和△DEF中,,
∴△ABC≌△DEF(SSS)
(2)由(1)知△ABC≌△DEF,
∴∠ACB=∠F,
∴∠EGC=180°-∠GEC-∠GCE=180°-∠GEC-∠F=∠D .
20.如图,延长DE至点F,使EF=BC,连接AC,AD,AF.易得CD=FD.
因为
所以△ABC≌△AEF(SAS).
所以AC=AF.
在△ACD与△AFD中,因为
所以△ACD≌△AFD(SSS).
所以五边形ABCDE的面积是
2S△ADF=2×·DF·AE=2××20×20=400(m2).
