八年级数学上册试题 14.2.3 其他判定两个三角形全等的条件-沪科版(含答案)
文档属性
| 名称 | 八年级数学上册试题 14.2.3 其他判定两个三角形全等的条件-沪科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 306.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 19:01:00 | ||
图片预览

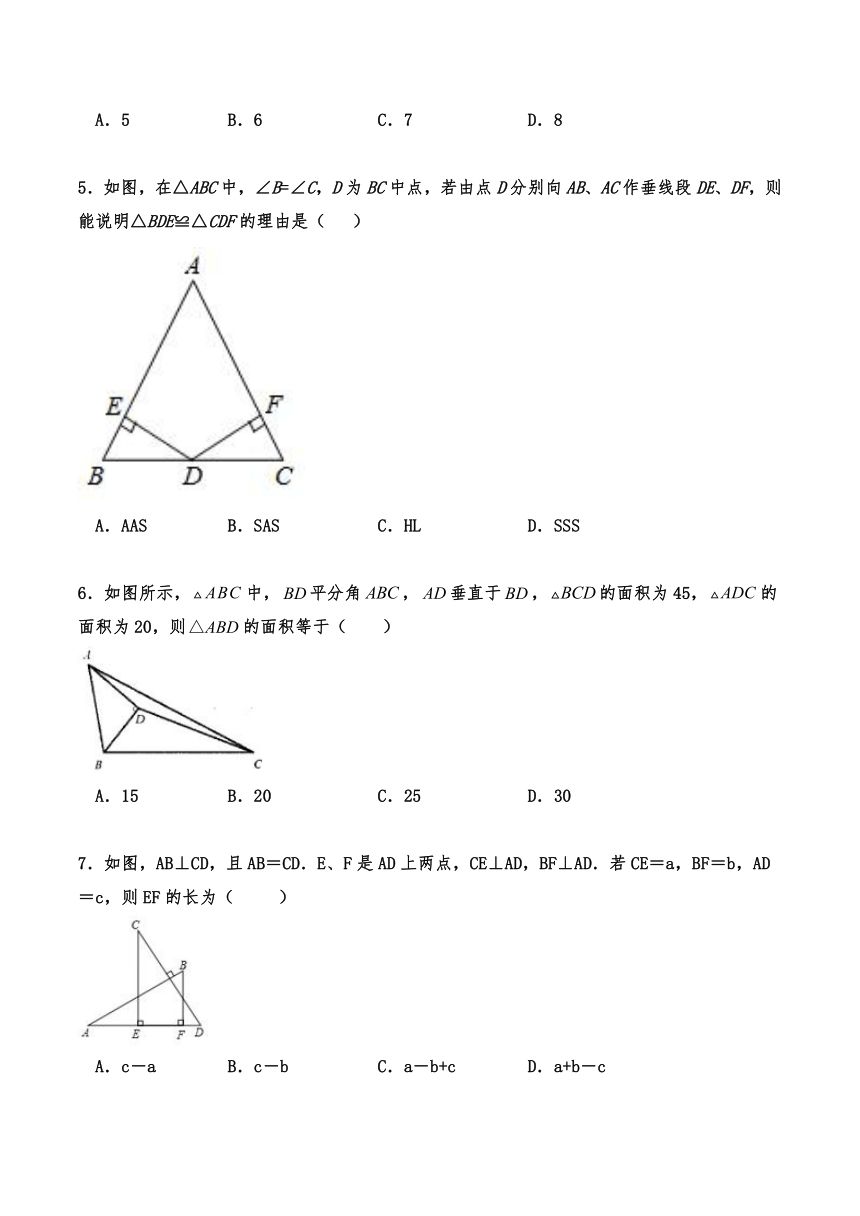


文档简介
14.2.3 其他判定两个三角形全等的条件
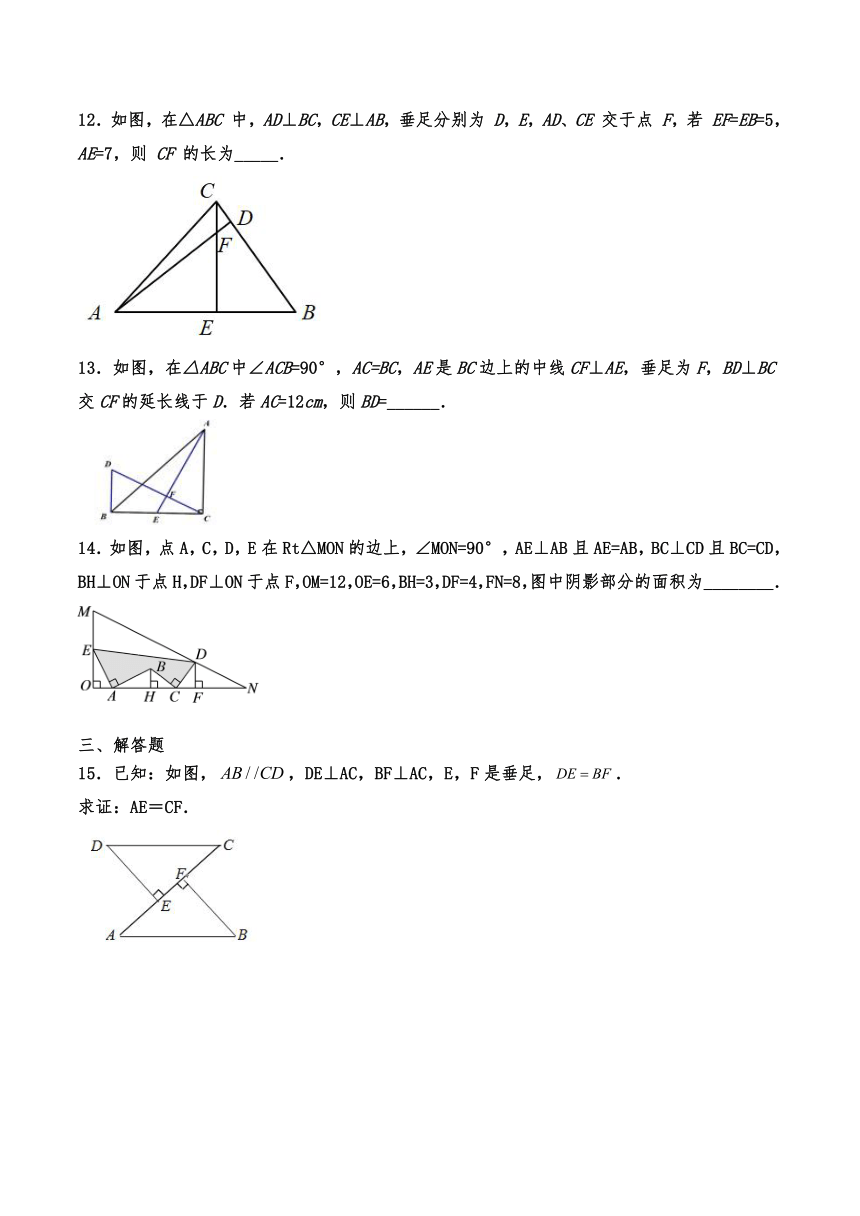
一、单选题
1.下列条件不能判定两个直角三角形全等的是( )
A.两条直角边对应相等 B.斜边和一锐角对应相等
C.斜边和一直角边对应相等 D.两个锐角对应相等
2.如图,已知点D,E,B在同一直线上,,,,,则△CDE和△EBA的面积之和是( )cm2
A.6 B.5 C.4 D.3
3.如图,在平面直角坐标系中,点的坐标为,点分别在轴的正半轴上,,则四边形的面积为( )
A. B. C. D.
4.如图,在四边形ABCD中,AB∥DC,AD∥BC,AC与BD相交于点O,M、A、O、C、N五点在一条直线上,MB⊥BC,ND⊥DA,则图中的全等三角形共有( )对.
A.5 B.6 C.7 D.8
5.如图,在△ABC中,∠B=∠C,D为BC中点,若由点D分别向AB、AC作垂线段DE、DF,则能说明△BDE≌△CDF的理由是( )
A.AAS B.SAS C.HL D.SSS
6.如图所示,中,平分角,垂直于,的面积为45,的面积为20,则的面积等于( )
A.15 B.20 C.25 D.30
7.如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,AD=c,则EF的长为( )
A.c-a B.c-b C.a-b+c D.a+b-c
8.如图,在△ABC中,BD平分∠ABC,AF⊥BD于点E,交BC于点F,点G是AC的中点,若BC=10,AB=7,则EG的长为( )
A.1.5 B.2 C.2.5 D.3.5
二、填空题
9.如图,,,垂足分别为、,,与交于点.写出由上述条件得到的两个不同类的结论__________.
10.梯形ABCD中,点E,F,G分别是BD,AC,DC的中点,已知:两底差是3,两腰的和是6,则△EFG的周长是______________.
11.如图,已知△ABC中,∠ABC=45°,F是高AD和BE 的交点,CD=4,则线段DF的长度为__________.
12.如图,在△ABC 中,AD⊥BC,CE⊥AB,垂足分别为 D,E,AD、CE 交于点 F,若 EF=EB=5, AE=7,则 CF 的长为_____.
13.如图,在△ABC中∠ACB=90°,AC=BC,AE是BC边上的中线CF⊥AE,垂足为F,BD⊥BC交CF的延长线于D.若AC=12cm,则BD=______.
14.如图,点A,C,D,E在Rt△MON的边上,∠MON=90°,AE⊥AB且AE=AB,BC⊥CD且BC=CD,BH⊥ON于点H,DF⊥ON于点F,OM=12,OE=6,BH=3,DF=4,FN=8,图中阴影部分的面积为________.
三、解答题
15.已知:如图,,DE⊥AC,BF⊥AC,E,F是垂足,.
求证:AE=CF.
16.要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示), 可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,请你运用自己所学知识说明他们的做法是正确的.
17.如图,在△ABC中,AB=AC,AD平分∠BAC,BF⊥AC于点F,交AD于点E,连接CE.
(1)求证:BE=CE;
(2)若AE=2BD,求∠BAC的度数.
18.如图,△ABC中,AB=AC,∠B的平分线交AC于D,E是BD延长线上的一点,且AE=AC.
(1)求证:AE//BC;
(2)若AD=DC=2,求BC的长.
19.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=48°,求∠BDE的度数.
20.如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).
(1)求k值与一次函数y=k1x+b的解析式;
(2)在x轴上有一动点P,求当PB+PC最小时P点坐标.
(3)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标;
答案
一、单选题
D.A.B.C.A.C.D.A.
二、填空题
9.PM=PN,∠PON=∠POM(答案不唯一).
10..
11.4.
12.2.
13.6cm.
14.50
三、解答题
15.
解:∵AB∥CD
∴∠C=∠A
∵DE⊥AC.BF⊥AC
∴∠DEC=∠BFA=90°
在△CDE和△ABF中
∴△CDE≌△ABF(AAS)
∴AF=CE
∴AF-EF=CE-EF
即AE=CF
16.
证明:∵BF⊥AB,DE⊥BD,
∴∠ABC=∠BDE
又∵CD=BC,∠ACB=∠DCE
∴△EDC≌△ABC(ASA),
∴DE=BA.
17.
证明:(1)∵AB=AC,AD平分∠BAC,
∴BD=CD,AD⊥BC,
∴BE=CE;
(2)∵AB=AC,AD平分∠BAC,
∴BD=CD,
∴BC=2BD,
又∵AE=2BD,
∴AE=BC,
∵BF⊥AC,AD⊥BC,
∴∠ACD+∠DAC=90°,∠ACD+∠CBF=90°,
∴∠CBF=∠DAC,
在△AEF和△BCF中,
,
∴△AEF≌△BCF(AAS),
∴AF=BF,
又∵BF⊥AF,
∴∠BAC=45°.
18.
证明:(1)∵AB=AC AE=AC,
∴ AE=AB,
∴∠ABE=∠AEB,
∵BD平分∠ABC,
∴∠ABE=∠EBC,
∴∠AEB=∠EBC,
∴AE∥BC;
(2)∵AE∥BC,
∴∠E=∠EBC,
在△ADE和△CDB中,
∵AD=CD ∠E=∠EBC ∠ADE=∠BDC,
∴△ADE≌△CDB,
∴AE=BC=AC,
∵ AE=AC,AD=DC=2,
∴BC=AE=4.
19.
解:(1)证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
∴△AEC≌△BED(ASA).
(2)∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=48°,
∴∠C=∠EDC=66°,
∴∠BDE=∠C=66°.
20.
解:(1)由题意,将点C(3,4)代入y=kx中,得:4=3k,
解得:k= ,
再将点C(3,4)、点A(﹣3,0)代入y=k1x+b中,得:
,
解得:,
∴函数y=k1x+b的解析式为:y=x+2;
(2)如图,作点B关于x轴对称的点B',连接B'C,交x轴于点P,此时PB+PC最小,
在y=x+2中,令x=0,则y=2,
∴B(0,2),则B'(0,﹣2),
设直线B'C的解析式为y=k2x﹣2,
将C(3,4)代入得:4=3k2﹣2,解得:k2=2,
∴直线B'C的解析式为y=2x﹣2,
令y=0,由0=2x﹣2得:x=1,
∴点P坐标为(1,0);
(3)根据题意,OA=3,OB=2,分两种情况:
①当∠DAB=90°时,DA=AB,
过点D作DM⊥x轴于E,
∵∠DAM+∠BAO=90°,∠BAO+∠ABO=90°,
∴∠DAM=∠ABO,
∵∠DMA=∠AOB=90°,DA=AB,
∴△DAM≌△ABO(AAS),
∴DM=OA=3,MA=OB=2,
∴D(﹣5,3);
②当∠D'BA=90°时,D'B=AB,
过D'作D'N⊥y轴于N,
同理可证△D'BN≌△BAO(AAS),
∴BN=OA=3,D'N=OB=2,
∴D'(﹣2,5),
故点D的坐标为(﹣5,3)或(﹣2,5).
一、单选题
1.下列条件不能判定两个直角三角形全等的是( )
A.两条直角边对应相等 B.斜边和一锐角对应相等
C.斜边和一直角边对应相等 D.两个锐角对应相等
2.如图,已知点D,E,B在同一直线上,,,,,则△CDE和△EBA的面积之和是( )cm2
A.6 B.5 C.4 D.3
3.如图,在平面直角坐标系中,点的坐标为,点分别在轴的正半轴上,,则四边形的面积为( )
A. B. C. D.
4.如图,在四边形ABCD中,AB∥DC,AD∥BC,AC与BD相交于点O,M、A、O、C、N五点在一条直线上,MB⊥BC,ND⊥DA,则图中的全等三角形共有( )对.
A.5 B.6 C.7 D.8
5.如图,在△ABC中,∠B=∠C,D为BC中点,若由点D分别向AB、AC作垂线段DE、DF,则能说明△BDE≌△CDF的理由是( )
A.AAS B.SAS C.HL D.SSS
6.如图所示,中,平分角,垂直于,的面积为45,的面积为20,则的面积等于( )
A.15 B.20 C.25 D.30
7.如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,AD=c,则EF的长为( )
A.c-a B.c-b C.a-b+c D.a+b-c
8.如图,在△ABC中,BD平分∠ABC,AF⊥BD于点E,交BC于点F,点G是AC的中点,若BC=10,AB=7,则EG的长为( )
A.1.5 B.2 C.2.5 D.3.5
二、填空题
9.如图,,,垂足分别为、,,与交于点.写出由上述条件得到的两个不同类的结论__________.
10.梯形ABCD中,点E,F,G分别是BD,AC,DC的中点,已知:两底差是3,两腰的和是6,则△EFG的周长是______________.
11.如图,已知△ABC中,∠ABC=45°,F是高AD和BE 的交点,CD=4,则线段DF的长度为__________.
12.如图,在△ABC 中,AD⊥BC,CE⊥AB,垂足分别为 D,E,AD、CE 交于点 F,若 EF=EB=5, AE=7,则 CF 的长为_____.
13.如图,在△ABC中∠ACB=90°,AC=BC,AE是BC边上的中线CF⊥AE,垂足为F,BD⊥BC交CF的延长线于D.若AC=12cm,则BD=______.
14.如图,点A,C,D,E在Rt△MON的边上,∠MON=90°,AE⊥AB且AE=AB,BC⊥CD且BC=CD,BH⊥ON于点H,DF⊥ON于点F,OM=12,OE=6,BH=3,DF=4,FN=8,图中阴影部分的面积为________.
三、解答题
15.已知:如图,,DE⊥AC,BF⊥AC,E,F是垂足,.
求证:AE=CF.
16.要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示), 可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,请你运用自己所学知识说明他们的做法是正确的.
17.如图,在△ABC中,AB=AC,AD平分∠BAC,BF⊥AC于点F,交AD于点E,连接CE.
(1)求证:BE=CE;
(2)若AE=2BD,求∠BAC的度数.
18.如图,△ABC中,AB=AC,∠B的平分线交AC于D,E是BD延长线上的一点,且AE=AC.
(1)求证:AE//BC;
(2)若AD=DC=2,求BC的长.
19.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=48°,求∠BDE的度数.
20.如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).
(1)求k值与一次函数y=k1x+b的解析式;
(2)在x轴上有一动点P,求当PB+PC最小时P点坐标.
(3)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标;
答案
一、单选题
D.A.B.C.A.C.D.A.
二、填空题
9.PM=PN,∠PON=∠POM(答案不唯一).
10..
11.4.
12.2.
13.6cm.
14.50
三、解答题
15.
解:∵AB∥CD
∴∠C=∠A
∵DE⊥AC.BF⊥AC
∴∠DEC=∠BFA=90°
在△CDE和△ABF中
∴△CDE≌△ABF(AAS)
∴AF=CE
∴AF-EF=CE-EF
即AE=CF
16.
证明:∵BF⊥AB,DE⊥BD,
∴∠ABC=∠BDE
又∵CD=BC,∠ACB=∠DCE
∴△EDC≌△ABC(ASA),
∴DE=BA.
17.
证明:(1)∵AB=AC,AD平分∠BAC,
∴BD=CD,AD⊥BC,
∴BE=CE;
(2)∵AB=AC,AD平分∠BAC,
∴BD=CD,
∴BC=2BD,
又∵AE=2BD,
∴AE=BC,
∵BF⊥AC,AD⊥BC,
∴∠ACD+∠DAC=90°,∠ACD+∠CBF=90°,
∴∠CBF=∠DAC,
在△AEF和△BCF中,
,
∴△AEF≌△BCF(AAS),
∴AF=BF,
又∵BF⊥AF,
∴∠BAC=45°.
18.
证明:(1)∵AB=AC AE=AC,
∴ AE=AB,
∴∠ABE=∠AEB,
∵BD平分∠ABC,
∴∠ABE=∠EBC,
∴∠AEB=∠EBC,
∴AE∥BC;
(2)∵AE∥BC,
∴∠E=∠EBC,
在△ADE和△CDB中,
∵AD=CD ∠E=∠EBC ∠ADE=∠BDC,
∴△ADE≌△CDB,
∴AE=BC=AC,
∵ AE=AC,AD=DC=2,
∴BC=AE=4.
19.
解:(1)证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
∴△AEC≌△BED(ASA).
(2)∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=48°,
∴∠C=∠EDC=66°,
∴∠BDE=∠C=66°.
20.
解:(1)由题意,将点C(3,4)代入y=kx中,得:4=3k,
解得:k= ,
再将点C(3,4)、点A(﹣3,0)代入y=k1x+b中,得:
,
解得:,
∴函数y=k1x+b的解析式为:y=x+2;
(2)如图,作点B关于x轴对称的点B',连接B'C,交x轴于点P,此时PB+PC最小,
在y=x+2中,令x=0,则y=2,
∴B(0,2),则B'(0,﹣2),
设直线B'C的解析式为y=k2x﹣2,
将C(3,4)代入得:4=3k2﹣2,解得:k2=2,
∴直线B'C的解析式为y=2x﹣2,
令y=0,由0=2x﹣2得:x=1,
∴点P坐标为(1,0);
(3)根据题意,OA=3,OB=2,分两种情况:
①当∠DAB=90°时,DA=AB,
过点D作DM⊥x轴于E,
∵∠DAM+∠BAO=90°,∠BAO+∠ABO=90°,
∴∠DAM=∠ABO,
∵∠DMA=∠AOB=90°,DA=AB,
∴△DAM≌△ABO(AAS),
∴DM=OA=3,MA=OB=2,
∴D(﹣5,3);
②当∠D'BA=90°时,D'B=AB,
过D'作D'N⊥y轴于N,
同理可证△D'BN≌△BAO(AAS),
∴BN=OA=3,D'N=OB=2,
∴D'(﹣2,5),
故点D的坐标为(﹣5,3)或(﹣2,5).
