八年级数学上册试题14.2.5 全等三角形的判定方法的综合运用-沪科版(含答案)
文档属性
| 名称 | 八年级数学上册试题14.2.5 全等三角形的判定方法的综合运用-沪科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 273.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 20:00:48 | ||
图片预览


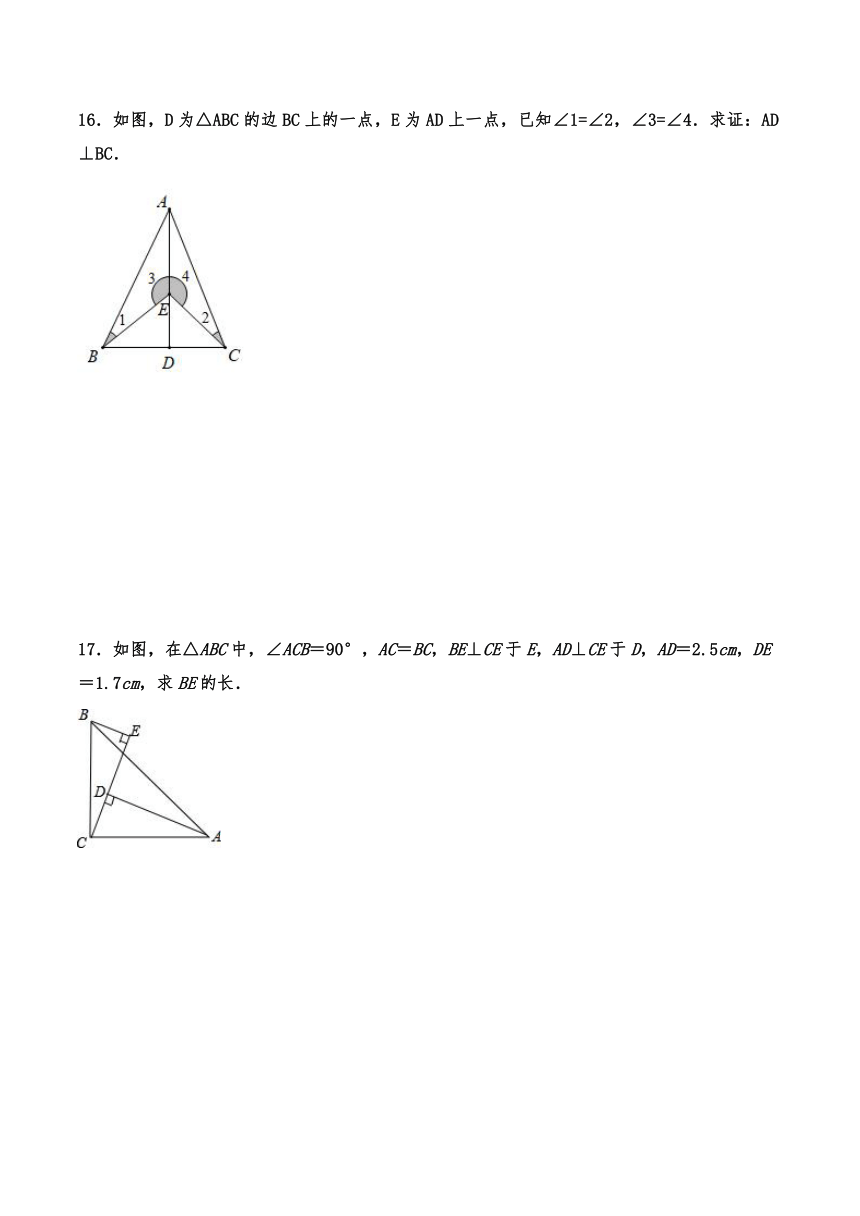
文档简介
14.2.5 全等三角形的判定方法的综合运用
一、单选题
1.如图,6个边长相等正方形的组合图形,则的度数( )
A.45° B.90° C.135° D.225°
2.下列说法正确的是( )
A.在中,若,则是直角三角形
B.每条边都相等的多边形是正多边形
C.所有正方形都是全等图形
D.如果两个三角形有两边和一角分别对应相等,那么这两个三角形全等
3.下列命题中,正确的是( )
A.有一角和两边对应相等的两个三角形全等
B.有两角和一边对应相等的两个三角形全等
C.有三个角对应相等的两个三角形全等
D.以上答案都不对
4.如图,已知,,添加下列条件仍不能证明的是( )
A. B. C. D.
5.如图,已知AB=DB,∠ABD=∠CBE,有下列条件:①BE=BC,②∠D=∠BAC,③∠C=∠E,④∠CBE=∠1,⑤AC=DE中,添加其中一条,能使△ABC≌△DBE的有()
A.1 B.2 C.3 D.4
6.已知:如图,是内部的一条射线,是射线上任意一点,,,垂足分别为,.有下列条件:①;②;③;④.其中,能判定是的平分线的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,和中,点,,,在同一直线上,在①,②,③,④,⑤五个条件中,能使与全等的条件的序号是( )
A.①②③ B.①②④ C.①③④ D.③④⑤
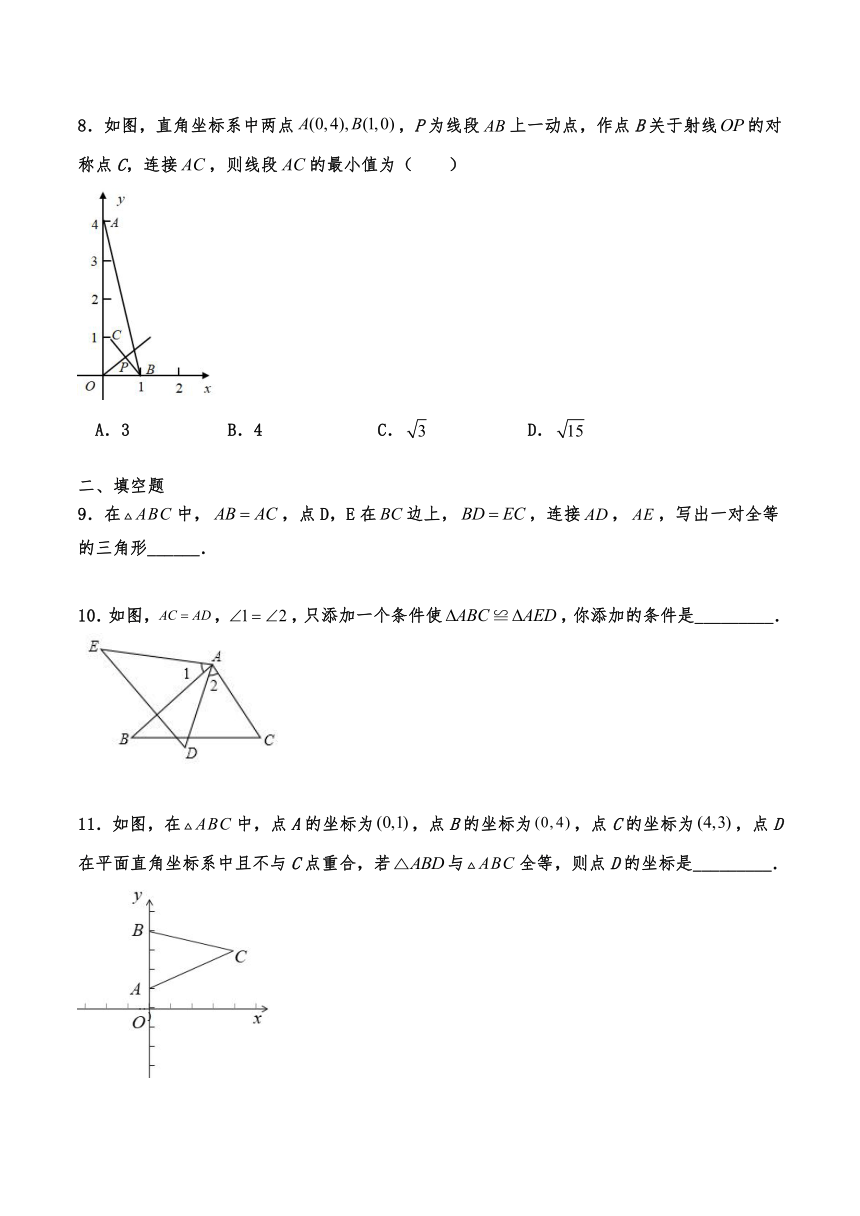
8.如图,直角坐标系中两点,P为线段上一动点,作点B关于射线的对称点C,连接,则线段的最小值为( )
A.3 B.4 C. D.
二、填空题
9.在中,,点D,E在边上,,连接,,写出一对全等的三角形______.
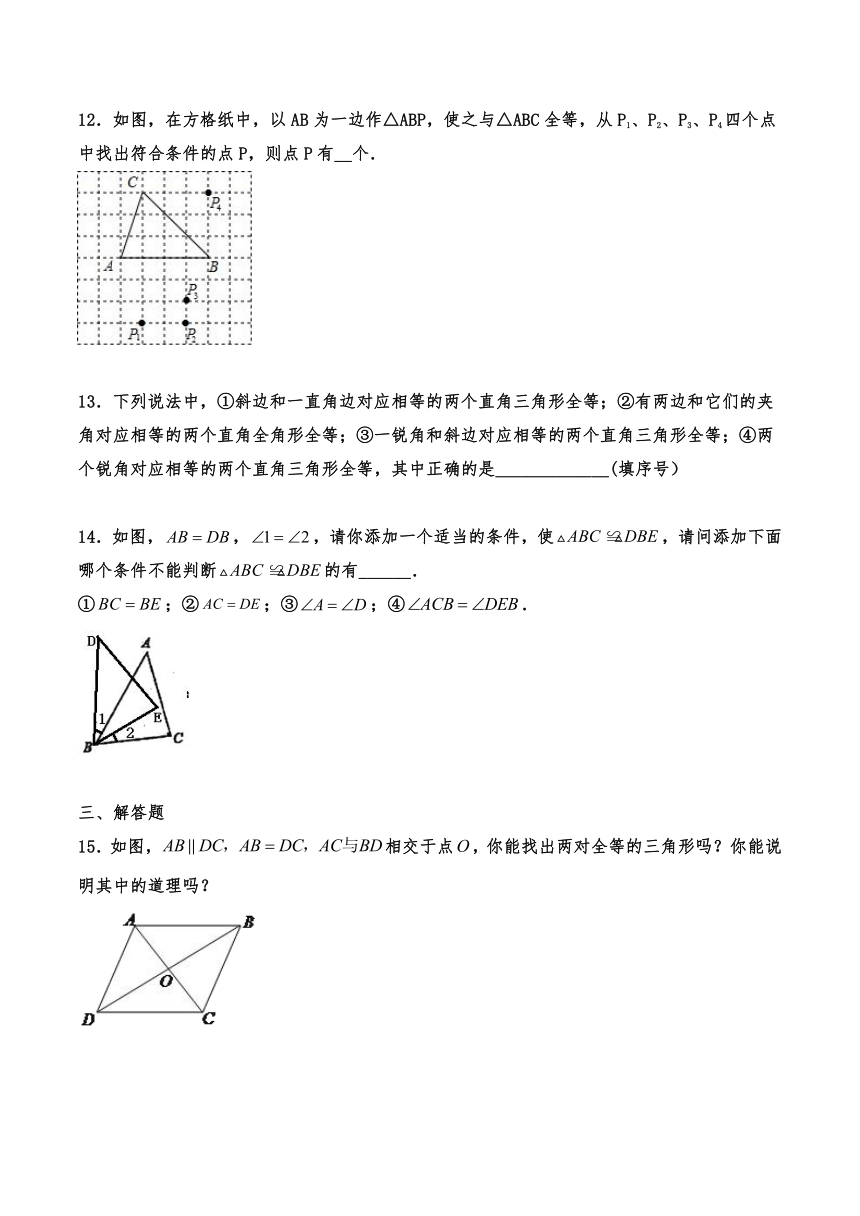
10.如图,,,只添加一个条件使,你添加的条件是_________.
11.如图,在中,点A的坐标为,点B的坐标为,点C的坐标为,点D在平面直角坐标系中且不与C点重合,若与全等,则点D的坐标是_________.
12.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1、P2、P3、P4四个点中找出符合条件的点P,则点P有__个.
13.下列说法中,①斜边和一直角边对应相等的两个直角三角形全等;②有两边和它们的夹角对应相等的两个直角全角形全等;③一锐角和斜边对应相等的两个直角三角形全等;④两个锐角对应相等的两个直角三角形全等,其中正确的是_____________(填序号)
14.如图,,,请你添加一个适当的条件,使,请问添加下面哪个条件不能判断的有______.
①;②;③;④.
三、解答题
15.如图,相交于点,你能找出两对全等的三角形吗?你能说明其中的道理吗?
16.如图,D为△ABC的边BC上的一点,E为AD上一点,已知∠1=∠2,∠3=∠4.求证:AD⊥BC.
17.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=2.5cm,DE=1.7cm,求BE的长.
18.求证:全等三角形的对应角平分线相等.
(1)在图②中,作出相应的角平分线,保留作图痕迹;
(2)根据题意,写出已知、求证,并加以证明。
19.如图,AB//CD,∠B=∠D,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)试判断AD与BE有怎样的位置关系,并说明理由;
(2)试说明△AOD≌△EOC.
20.我们知道如果两个三角形的两边及一边的对角对应相等,这两个三角形不一定全等,简称“SSA”不成立.
(1)如果这两个三角形都是直角三角形,则是成立的.如图1,在和中,AB=DE,AC=DF,∠C=∠F=90°.求证:;
(2)如果这两个三角形都是锐角三角形,也是成立的.如图2,在锐角和锐角中,AB=DE,AC=DF,∠B=∠E.求证:;
(3)如果这两个三角形都是钝角三角形,且这两个三角形的两边及一边的对角对应相等,那么这两个钝角三角形全等吗 请直接给出结论,不必证明.
答案
一、单选题
C.A.B.B.D.D.C.A.
二、填空题
9..(答案不唯一,满足题意即可)
10.∠C=∠D或∠B=∠E或AB=AE.
11.(-4,3),(4,2),(-4,2).
12.2.
13.①②③.
14.②.
三、解答题
15.
四对全等的三角形,分别为
理由分别是:
的理由:
∴(ASA);
的理由:
∵,
∴,DO=BO
即,
∴(SAS);
的理由:
即,
∴(SAS)
的理由:
即,
∴(SAS).
16.
证明:证明:在和中,
∴,
∴,
∵ 在和中,
∴ ,
∴
∵,
∴,
∴ .
17.
解:∵BE⊥CE于E,AD⊥CE于D
∴∠E=∠ADC=90°
∵∠BCE+∠ACE=∠DAC+∠ACE=90°
∴∠BCE=∠DAC
∵AC=BC
∴△ACD≌△CBE
∴CE=AD,BE=CD=2.5﹣1.7=0.8(cm).
18.
(1)如图,A’D’即为所求;
(2)已知,△ABC≌△A’B’C’,AD,A’D’分别是△△ABC,△A’B’C’的角平分线;
求证:AD=A’D’;
证明:∵△ABC≌△A’B’C’
∴AB=A’B’,∠B=∠B’,∠BAC=∠B’A’C’
∵AD,A’D’分别是△△ABC,△A’B’C’的角平分线
∴∠BAD=∠B’A’D’
∴△ABD≌△A’B’D(ASA)
∴AD=A’D’
即全等三角形的对应角平分线相等.
19.
(1)AD//BE,
理由:∵AB//CD,
∴∠B=∠DCE,
∵∠B=∠D,
∴∠DCE=∠D,
∴AD//BE;
(2)∵O是CD的中点,
∴DO=CO,
在△ADO和△ECO中,
∴△AOD≌△EOC(ASA).
20.
证明:(1)在和中,AB=DE,AC=DF,∠C=∠F=90°.
∴(HL);
(2)分别作AG⊥BC于G,DH⊥EF于H,
则∠BGA=∠EHD=90°,
∵AB=DE,∠B=∠E,
∴△ABG≌△DEH,
∴AG=DH.
在Rt△AGC与Rt△DHF中,
∵AG=DH,AC=DF.
∴△AGC≌△DHF(HL),
∴∠C=∠F,
在△ABC与△DEF中,
∵∠B=∠E,∠C=∠F,AC=DF,
∴△ABC≌△DEF(AAS);
(3)如果这两个三角形都是钝角三角形,且这两个三角形的两边及一边的对角对应相等,那么这两个钝角三角形全等.理由如下:
如图3,在钝角和钝角中,AB=DE,AC=DF,∠ABC=∠DEF.求证:.
如图,分别作AG⊥BC于G,DH⊥EF于H.
则∠BGA=∠EHD=90°,
∵∠ABC=∠DEF,
∴∠ABG=∠DEH,
∵AB=DE,
∴△ABG≌△DEH,
∴AG=DH.
在Rt△AGC与Rt△DHF中,
∵AG=DH,AC=DF.
∴△AGC≌△DHF(HL),
∴∠C=∠F,
在△ABC与△DEF中,
∵∠ABC=∠DEF,∠C=∠F,AC=DF,
∴△ABC≌△DEF(AAS).
一、单选题
1.如图,6个边长相等正方形的组合图形,则的度数( )
A.45° B.90° C.135° D.225°
2.下列说法正确的是( )
A.在中,若,则是直角三角形
B.每条边都相等的多边形是正多边形
C.所有正方形都是全等图形
D.如果两个三角形有两边和一角分别对应相等,那么这两个三角形全等
3.下列命题中,正确的是( )
A.有一角和两边对应相等的两个三角形全等
B.有两角和一边对应相等的两个三角形全等
C.有三个角对应相等的两个三角形全等
D.以上答案都不对
4.如图,已知,,添加下列条件仍不能证明的是( )
A. B. C. D.
5.如图,已知AB=DB,∠ABD=∠CBE,有下列条件:①BE=BC,②∠D=∠BAC,③∠C=∠E,④∠CBE=∠1,⑤AC=DE中,添加其中一条,能使△ABC≌△DBE的有()
A.1 B.2 C.3 D.4
6.已知:如图,是内部的一条射线,是射线上任意一点,,,垂足分别为,.有下列条件:①;②;③;④.其中,能判定是的平分线的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,和中,点,,,在同一直线上,在①,②,③,④,⑤五个条件中,能使与全等的条件的序号是( )
A.①②③ B.①②④ C.①③④ D.③④⑤
8.如图,直角坐标系中两点,P为线段上一动点,作点B关于射线的对称点C,连接,则线段的最小值为( )
A.3 B.4 C. D.
二、填空题
9.在中,,点D,E在边上,,连接,,写出一对全等的三角形______.
10.如图,,,只添加一个条件使,你添加的条件是_________.
11.如图,在中,点A的坐标为,点B的坐标为,点C的坐标为,点D在平面直角坐标系中且不与C点重合,若与全等,则点D的坐标是_________.
12.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1、P2、P3、P4四个点中找出符合条件的点P,则点P有__个.
13.下列说法中,①斜边和一直角边对应相等的两个直角三角形全等;②有两边和它们的夹角对应相等的两个直角全角形全等;③一锐角和斜边对应相等的两个直角三角形全等;④两个锐角对应相等的两个直角三角形全等,其中正确的是_____________(填序号)
14.如图,,,请你添加一个适当的条件,使,请问添加下面哪个条件不能判断的有______.
①;②;③;④.
三、解答题
15.如图,相交于点,你能找出两对全等的三角形吗?你能说明其中的道理吗?
16.如图,D为△ABC的边BC上的一点,E为AD上一点,已知∠1=∠2,∠3=∠4.求证:AD⊥BC.
17.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=2.5cm,DE=1.7cm,求BE的长.
18.求证:全等三角形的对应角平分线相等.
(1)在图②中,作出相应的角平分线,保留作图痕迹;
(2)根据题意,写出已知、求证,并加以证明。
19.如图,AB//CD,∠B=∠D,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)试判断AD与BE有怎样的位置关系,并说明理由;
(2)试说明△AOD≌△EOC.
20.我们知道如果两个三角形的两边及一边的对角对应相等,这两个三角形不一定全等,简称“SSA”不成立.
(1)如果这两个三角形都是直角三角形,则是成立的.如图1,在和中,AB=DE,AC=DF,∠C=∠F=90°.求证:;
(2)如果这两个三角形都是锐角三角形,也是成立的.如图2,在锐角和锐角中,AB=DE,AC=DF,∠B=∠E.求证:;
(3)如果这两个三角形都是钝角三角形,且这两个三角形的两边及一边的对角对应相等,那么这两个钝角三角形全等吗 请直接给出结论,不必证明.
答案
一、单选题
C.A.B.B.D.D.C.A.
二、填空题
9..(答案不唯一,满足题意即可)
10.∠C=∠D或∠B=∠E或AB=AE.
11.(-4,3),(4,2),(-4,2).
12.2.
13.①②③.
14.②.
三、解答题
15.
四对全等的三角形,分别为
理由分别是:
的理由:
∴(ASA);
的理由:
∵,
∴,DO=BO
即,
∴(SAS);
的理由:
即,
∴(SAS)
的理由:
即,
∴(SAS).
16.
证明:证明:在和中,
∴,
∴,
∵ 在和中,
∴ ,
∴
∵,
∴,
∴ .
17.
解:∵BE⊥CE于E,AD⊥CE于D
∴∠E=∠ADC=90°
∵∠BCE+∠ACE=∠DAC+∠ACE=90°
∴∠BCE=∠DAC
∵AC=BC
∴△ACD≌△CBE
∴CE=AD,BE=CD=2.5﹣1.7=0.8(cm).
18.
(1)如图,A’D’即为所求;
(2)已知,△ABC≌△A’B’C’,AD,A’D’分别是△△ABC,△A’B’C’的角平分线;
求证:AD=A’D’;
证明:∵△ABC≌△A’B’C’
∴AB=A’B’,∠B=∠B’,∠BAC=∠B’A’C’
∵AD,A’D’分别是△△ABC,△A’B’C’的角平分线
∴∠BAD=∠B’A’D’
∴△ABD≌△A’B’D(ASA)
∴AD=A’D’
即全等三角形的对应角平分线相等.
19.
(1)AD//BE,
理由:∵AB//CD,
∴∠B=∠DCE,
∵∠B=∠D,
∴∠DCE=∠D,
∴AD//BE;
(2)∵O是CD的中点,
∴DO=CO,
在△ADO和△ECO中,
∴△AOD≌△EOC(ASA).
20.
证明:(1)在和中,AB=DE,AC=DF,∠C=∠F=90°.
∴(HL);
(2)分别作AG⊥BC于G,DH⊥EF于H,
则∠BGA=∠EHD=90°,
∵AB=DE,∠B=∠E,
∴△ABG≌△DEH,
∴AG=DH.
在Rt△AGC与Rt△DHF中,
∵AG=DH,AC=DF.
∴△AGC≌△DHF(HL),
∴∠C=∠F,
在△ABC与△DEF中,
∵∠B=∠E,∠C=∠F,AC=DF,
∴△ABC≌△DEF(AAS);
(3)如果这两个三角形都是钝角三角形,且这两个三角形的两边及一边的对角对应相等,那么这两个钝角三角形全等.理由如下:
如图3,在钝角和钝角中,AB=DE,AC=DF,∠ABC=∠DEF.求证:.
如图,分别作AG⊥BC于G,DH⊥EF于H.
则∠BGA=∠EHD=90°,
∵∠ABC=∠DEF,
∴∠ABG=∠DEH,
∵AB=DE,
∴△ABG≌△DEH,
∴AG=DH.
在Rt△AGC与Rt△DHF中,
∵AG=DH,AC=DF.
∴△AGC≌△DHF(HL),
∴∠C=∠F,
在△ABC与△DEF中,
∵∠ABC=∠DEF,∠C=∠F,AC=DF,
∴△ABC≌△DEF(AAS).
