八年级数学上册试题 13.1三角形中的边角关系同步练习-沪科版(含答案)
文档属性
| 名称 | 八年级数学上册试题 13.1三角形中的边角关系同步练习-沪科版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 348.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 19:09:02 | ||
图片预览




文档简介
13.1三角形中的边角关系
第一课时
一、单选题
1.下列长度的三条线段中,能围成三角形的是( )
A.5cm,6cm,12cm B.3cm,4cm,5cm
C.4cm,6cm,10cm D.3cm,4cm,8cm
2.下面给出的四个三角形都有一部分被遮挡,其中不能判断三角形类型的是( )
A. B.
C. D.
3.已知三角形的三边长分别为a,b,c,化简得( )
A. B.
C. D.
4.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能是( )
A.都是锐角三角形 B.都是直角三角形
C.都是钝角三角形D.是一个直角三角形和一个钝角三角形
5.如图,AD是的中线,已知的周长为25cm,AB比AC长6cm,则的周长为( )
A.19cm B.22cm C.25cm D.31cm
二、填空题
6.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有________对
7.如图,在中,已知点、、分别为、、的中点,且,则________
8.如图,已知直线,直线垂直于,垂足为,直线交于点,,则_______.
9.三角形一边长为另一边长为且第三边长为偶数,则第三边的长为__________.
三、解答题
10.已知a,b,c是的三边长,且,若三角形的周长是小于18的偶数.
(1)求c的值;
(2)判断的形状.
11.已知a,b,c是三角形的三边长.
(1)化简:|a-b-c|+|b-c-a|+|c-a-b|;
(2)在(1)的条件下,若a=5,b=4,c=3,求这个式子的值.
12.如图所示,求的度数.
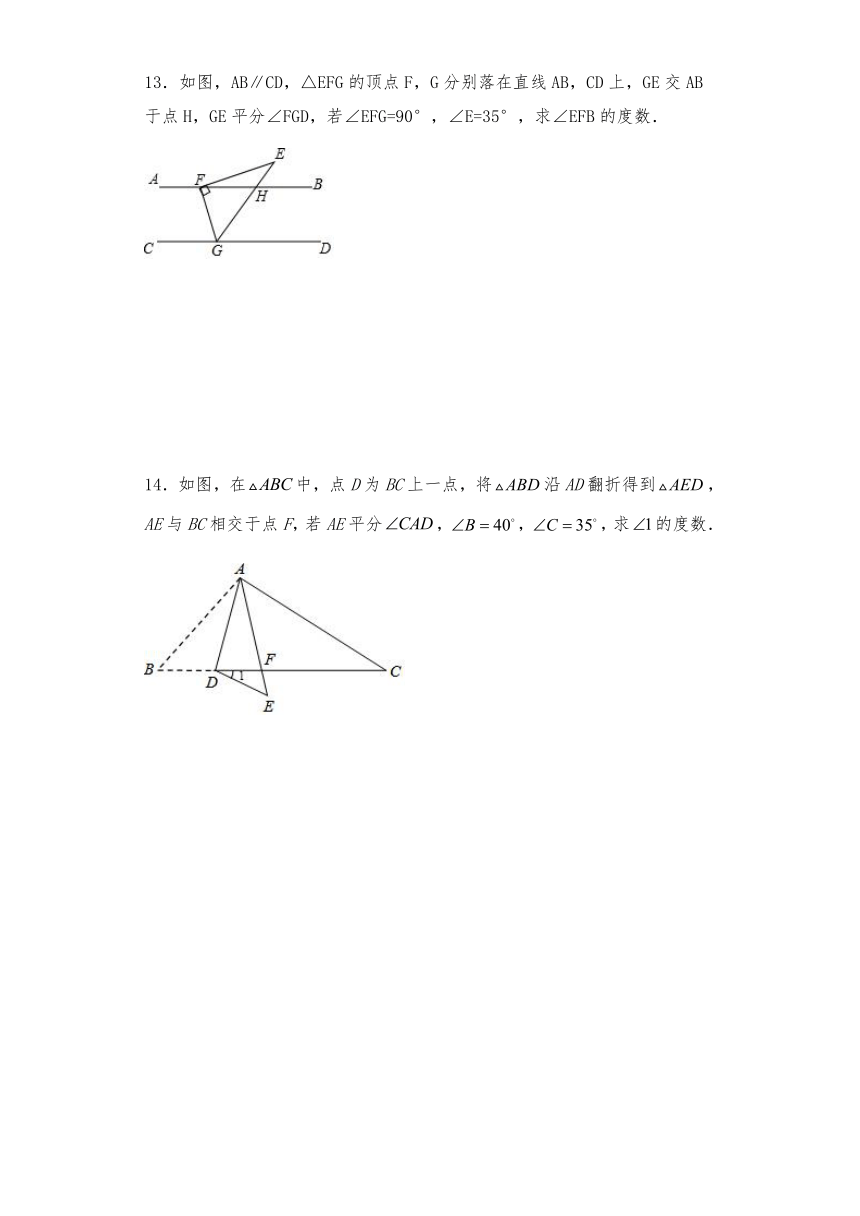
13.如图,AB∥CD,△EFG的顶点F,G分别落在直线AB,CD上,GE交AB于点H,GE平分∠FGD,若∠EFG=90°,∠E=35°,求∠EFB的度数.
14.如图,在中,点D为BC上一点,将沿AD翻折得到,AE与BC相交于点F,若AE平分,,,求的度数.
第二课时
一、单选题
1.如图,将一张含有角的三角形纸片的两个顶点叠放在矩形的两条对边上,若,则的大小为( )
A. B. C. D.
2.如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E,若∠A=54°,∠B=48°,则∠CDE的大小为( )
A.44° B.40° C.39° D.38°
3.下列各组线段不能组成三角形的是 ( )
A.4cm、4cm、5cm B.4cm、6cm、11cm
C.4cm、5cm、6cm D.5cm、12cm、13cm
4.已知三角形的三边长分别为2,a-1,4,则化简|a-3|+|a-7|的结果为( )
A.2a-10 B.10-2a
C.4 D.-4
5.如图,把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )
A.∠1=∠2+∠A B.∠1=2∠A+∠2
C.∠1=2∠2+2∠A D.2∠1=∠2+∠A
二、填空题
6.如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A=_____.
7.若a、b、c为三角形的三边,且a、b满足,则第三边c的取值范围是 .
8.如图所示,直线a∥b,∠1=35°,∠2=90°,则∠3的度数为________。
9.如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t=___________________,△APE的面积等于6.
三、解答题
10.用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长.
(2)能围成有一边的长是4cm的等腰三角形吗?若能,求出其他两边的长;若不能,请说明理由.
11.如图所示,已知AD,AE分别是△ADC和△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
12.如图,在△ABC中,BO、CO分别平分∠ABC和∠ACB.计算:
(1)若∠A=60°,求∠BOC的度数;
(2)若∠A=100°,则∠BOC的度数是多少?
(3)若∠A=120°,则∠BOC的度数又是多少?
(4)由(1)、(2)、(3),你发现了什么规律?请用一个等式将这个规律表示出来.
13.已知△ABC,如图,过点A画△ABC的角平分线AD、中线AE和高线AF.
14.如图BO、CO分别平分和,DE过点D且,,,求的周长.
第一课时答案
一、单选题
B.C.A.A.A.
二、填空题
6.3
7.1.
8.140°.
9.2或4或6.
三、解答题
10.
(1)∵的周长为,且周长小于18,即,.
又∵三角形的周长是小于18的偶数,即为偶数,
∴c为小于8的偶数,则c可以是2,4,6.
∵当时,,不能构成三角形,故舍去,
∴c的值为4或6.
(2)由(1)得当时,有;当时,有,
为等腰三角形.
11.
(1)∵a、b、c是三角形的三边长,
∴a﹣b﹣c<0,b﹣c﹣a<0,c﹣a﹣b<0,
∴原式=﹣a+b+c﹣b+a+c﹣c+a+b
=a+b+c;
(2)当a=5,b=4,c=3时,
原式=5+4+3=12.
12.
解:∵∠1=∠A+∠B,∠2=∠C+∠D,∠3=∠E+∠F,
又∵∠1+∠2+∠3=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
13.
∵∠EFG=90°,∠E=35°,
∴∠FGH=55°,
∵GE平分∠FGD,AB∥CD,
∴∠FHG=∠HGD=∠FGH=55°,
∵∠FHG是△EFH的外角,
∴∠EFB=55°﹣35°=20°.
14.
解:,,,
.
又平分,
.
由翻折得:,,
,
.
又,
.
第二课时答案
一、单选题
A.C.B.C.B
二、填空题
6.40°.
7.1<c<5.
8.(125°
9.1.5或5或9.
三、解答题
10.
(1)设底边长为xcm,则腰长为2xcm,,
依题意,得,
解得,
∴,
∴三角形三边的长为cm、cm、cm;
(2)若腰长为4cm,则底边长为18-4-4=10cm,
而4+4<10,所以不能围成腰长为4cm的等腰三角形,
若底边长为4cm,则腰长为=7cm,
此时能围成等腰三角形,三边长分别为4cm、7cm、7cm.
11.
∵∠BAC=90°,AD是边BC上的高,
∴AB AC=BC AD,
∴AD= =4.8(cm),
即AD的长度为4.8cm;
(2)如图,∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,
∴S△ABC=AB AC=×6×8=24(cm2).
又∵AE是边BC的中线,
∴BE=EC,
∴BE AD=EC AD,即S△ABE=S△AEC,
∴S△ABE=S△ABC=12(cm2).
∴△ABE的面积是12cm2.
(3)∵AE为BC边上的中线,
∴BE=CE,
∴△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=8-6=2(cm),
即△ACE和△ABE的周长的差是2cm.
12.
(1)∵BO、CO分别平分∠ABC和∠ACB,∠A=60°,
∴∠CBO+∠BCO=(180°﹣∠A)=(180°﹣60°)=60°,
∴∠BOC=180°﹣(∠CBO+∠BCO)=180°﹣60°=120°;
(2)同理,若∠A=100°,则∠BOC=180°﹣(180°﹣∠A)=90°+∠A=140°;
(3)同理,若∠A=120°,则∠BOC=180°﹣(180°﹣∠A)=90°+∠A=150°;
(4)由(1)、(2)、(3),发现:∠BOC=180°﹣(180°﹣∠A)=90°+∠A.
13.
解:由题意画图可得:
14.
∵BO、CO分别平分和,
,,
又.
,,
,,
,,
∴周长
第一课时
一、单选题
1.下列长度的三条线段中,能围成三角形的是( )
A.5cm,6cm,12cm B.3cm,4cm,5cm
C.4cm,6cm,10cm D.3cm,4cm,8cm
2.下面给出的四个三角形都有一部分被遮挡,其中不能判断三角形类型的是( )
A. B.
C. D.
3.已知三角形的三边长分别为a,b,c,化简得( )
A. B.
C. D.
4.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能是( )
A.都是锐角三角形 B.都是直角三角形
C.都是钝角三角形D.是一个直角三角形和一个钝角三角形
5.如图,AD是的中线,已知的周长为25cm,AB比AC长6cm,则的周长为( )
A.19cm B.22cm C.25cm D.31cm
二、填空题
6.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有________对
7.如图,在中,已知点、、分别为、、的中点,且,则________
8.如图,已知直线,直线垂直于,垂足为,直线交于点,,则_______.
9.三角形一边长为另一边长为且第三边长为偶数,则第三边的长为__________.
三、解答题
10.已知a,b,c是的三边长,且,若三角形的周长是小于18的偶数.
(1)求c的值;
(2)判断的形状.
11.已知a,b,c是三角形的三边长.
(1)化简:|a-b-c|+|b-c-a|+|c-a-b|;
(2)在(1)的条件下,若a=5,b=4,c=3,求这个式子的值.
12.如图所示,求的度数.
13.如图,AB∥CD,△EFG的顶点F,G分别落在直线AB,CD上,GE交AB于点H,GE平分∠FGD,若∠EFG=90°,∠E=35°,求∠EFB的度数.
14.如图,在中,点D为BC上一点,将沿AD翻折得到,AE与BC相交于点F,若AE平分,,,求的度数.
第二课时
一、单选题
1.如图,将一张含有角的三角形纸片的两个顶点叠放在矩形的两条对边上,若,则的大小为( )
A. B. C. D.
2.如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E,若∠A=54°,∠B=48°,则∠CDE的大小为( )
A.44° B.40° C.39° D.38°
3.下列各组线段不能组成三角形的是 ( )
A.4cm、4cm、5cm B.4cm、6cm、11cm
C.4cm、5cm、6cm D.5cm、12cm、13cm
4.已知三角形的三边长分别为2,a-1,4,则化简|a-3|+|a-7|的结果为( )
A.2a-10 B.10-2a
C.4 D.-4
5.如图,把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )
A.∠1=∠2+∠A B.∠1=2∠A+∠2
C.∠1=2∠2+2∠A D.2∠1=∠2+∠A
二、填空题
6.如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A=_____.
7.若a、b、c为三角形的三边,且a、b满足,则第三边c的取值范围是 .
8.如图所示,直线a∥b,∠1=35°,∠2=90°,则∠3的度数为________。
9.如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t=___________________,△APE的面积等于6.
三、解答题
10.用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长.
(2)能围成有一边的长是4cm的等腰三角形吗?若能,求出其他两边的长;若不能,请说明理由.
11.如图所示,已知AD,AE分别是△ADC和△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
12.如图,在△ABC中,BO、CO分别平分∠ABC和∠ACB.计算:
(1)若∠A=60°,求∠BOC的度数;
(2)若∠A=100°,则∠BOC的度数是多少?
(3)若∠A=120°,则∠BOC的度数又是多少?
(4)由(1)、(2)、(3),你发现了什么规律?请用一个等式将这个规律表示出来.
13.已知△ABC,如图,过点A画△ABC的角平分线AD、中线AE和高线AF.
14.如图BO、CO分别平分和,DE过点D且,,,求的周长.
第一课时答案
一、单选题
B.C.A.A.A.
二、填空题
6.3
7.1.
8.140°.
9.2或4或6.
三、解答题
10.
(1)∵的周长为,且周长小于18,即,.
又∵三角形的周长是小于18的偶数,即为偶数,
∴c为小于8的偶数,则c可以是2,4,6.
∵当时,,不能构成三角形,故舍去,
∴c的值为4或6.
(2)由(1)得当时,有;当时,有,
为等腰三角形.
11.
(1)∵a、b、c是三角形的三边长,
∴a﹣b﹣c<0,b﹣c﹣a<0,c﹣a﹣b<0,
∴原式=﹣a+b+c﹣b+a+c﹣c+a+b
=a+b+c;
(2)当a=5,b=4,c=3时,
原式=5+4+3=12.
12.
解:∵∠1=∠A+∠B,∠2=∠C+∠D,∠3=∠E+∠F,
又∵∠1+∠2+∠3=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
13.
∵∠EFG=90°,∠E=35°,
∴∠FGH=55°,
∵GE平分∠FGD,AB∥CD,
∴∠FHG=∠HGD=∠FGH=55°,
∵∠FHG是△EFH的外角,
∴∠EFB=55°﹣35°=20°.
14.
解:,,,
.
又平分,
.
由翻折得:,,
,
.
又,
.
第二课时答案
一、单选题
A.C.B.C.B
二、填空题
6.40°.
7.1<c<5.
8.(125°
9.1.5或5或9.
三、解答题
10.
(1)设底边长为xcm,则腰长为2xcm,,
依题意,得,
解得,
∴,
∴三角形三边的长为cm、cm、cm;
(2)若腰长为4cm,则底边长为18-4-4=10cm,
而4+4<10,所以不能围成腰长为4cm的等腰三角形,
若底边长为4cm,则腰长为=7cm,
此时能围成等腰三角形,三边长分别为4cm、7cm、7cm.
11.
∵∠BAC=90°,AD是边BC上的高,
∴AB AC=BC AD,
∴AD= =4.8(cm),
即AD的长度为4.8cm;
(2)如图,∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,
∴S△ABC=AB AC=×6×8=24(cm2).
又∵AE是边BC的中线,
∴BE=EC,
∴BE AD=EC AD,即S△ABE=S△AEC,
∴S△ABE=S△ABC=12(cm2).
∴△ABE的面积是12cm2.
(3)∵AE为BC边上的中线,
∴BE=CE,
∴△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=8-6=2(cm),
即△ACE和△ABE的周长的差是2cm.
12.
(1)∵BO、CO分别平分∠ABC和∠ACB,∠A=60°,
∴∠CBO+∠BCO=(180°﹣∠A)=(180°﹣60°)=60°,
∴∠BOC=180°﹣(∠CBO+∠BCO)=180°﹣60°=120°;
(2)同理,若∠A=100°,则∠BOC=180°﹣(180°﹣∠A)=90°+∠A=140°;
(3)同理,若∠A=120°,则∠BOC=180°﹣(180°﹣∠A)=90°+∠A=150°;
(4)由(1)、(2)、(3),发现:∠BOC=180°﹣(180°﹣∠A)=90°+∠A.
13.
解:由题意画图可得:
14.
∵BO、CO分别平分和,
,,
又.
,,
,,
,,
∴周长
