八年级数学上册试题 14.1全等三角形同步练习-沪科版(含答案)
文档属性
| 名称 | 八年级数学上册试题 14.1全等三角形同步练习-沪科版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 371.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 19:22:15 | ||
图片预览


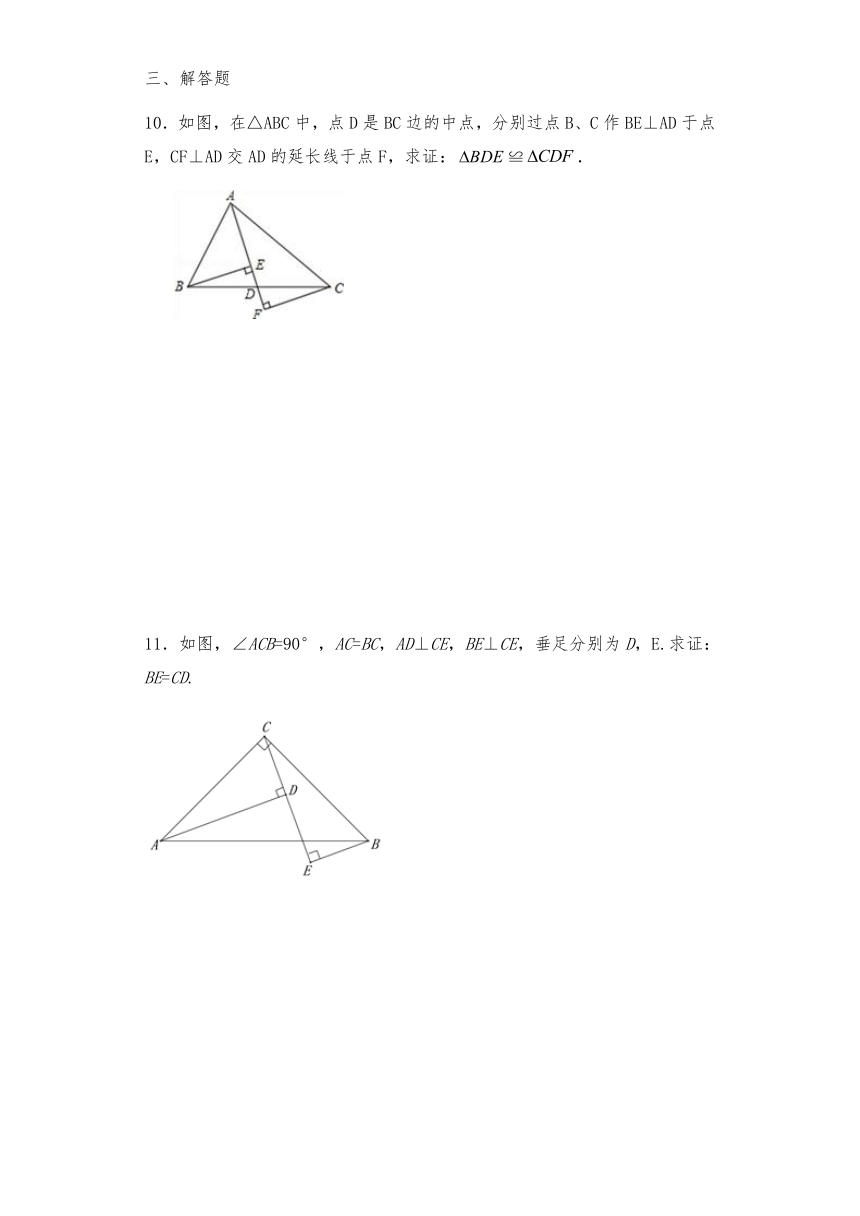

文档简介
14.1全等三角形
第一课时
一、单选题
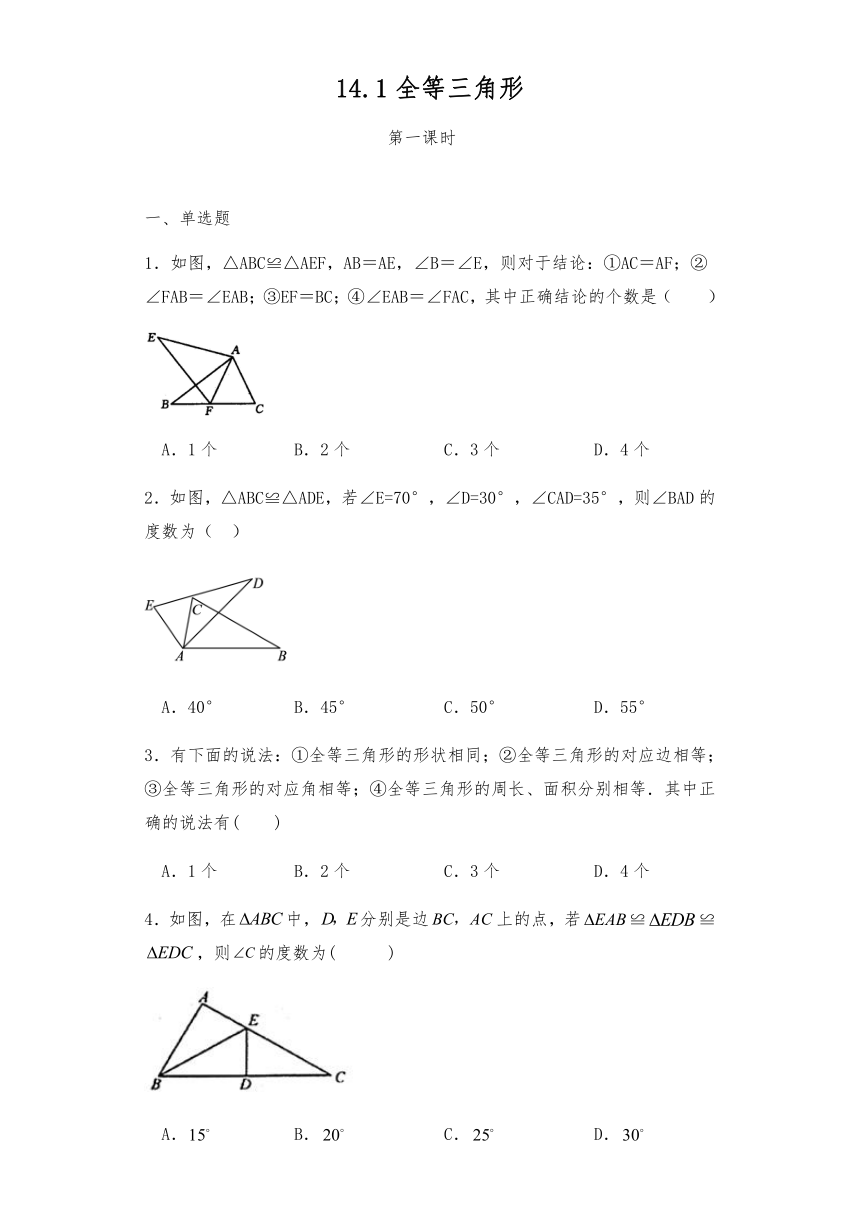
1.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
2.如图,△ABC≌△ADE,若∠E=70°,∠D=30°,∠CAD=35°,则∠BAD的度数为( )
A.40° B.45° C.50° D.55°
3.有下面的说法:①全等三角形的形状相同;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
4.如图,在中,分别是边上的点,若≌≌,则的度数为( )
A. B. C. D.
5.已知图中的两个三角形全等,则∠α的度数是( )
A.72° B.60° C.58° D.50°
二、填空题
6.如图,△ACE≌△DBF,点A、B、C、D共线,若AC=5,BC=2,则CD的长度等于________.
7.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为_______________°.
8.已知,且的周长为25,,则____________.
9.如图,在平面直角坐标系中,△AOB≌△COD,则点D的坐标是____________.
三、解答题
10.如图,在△ABC中,点D是BC边的中点,分别过点B、C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:≌.
11.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.求证:BE=CD.
12.如图,锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,DF=DC.
求证:BF=AC.
13.如图,△AOB,△COD是等腰直角三角形,点D在AB上,
(1)求证:△AOC≌△BOD;
(2)若AD=3,BD=1,求CD.
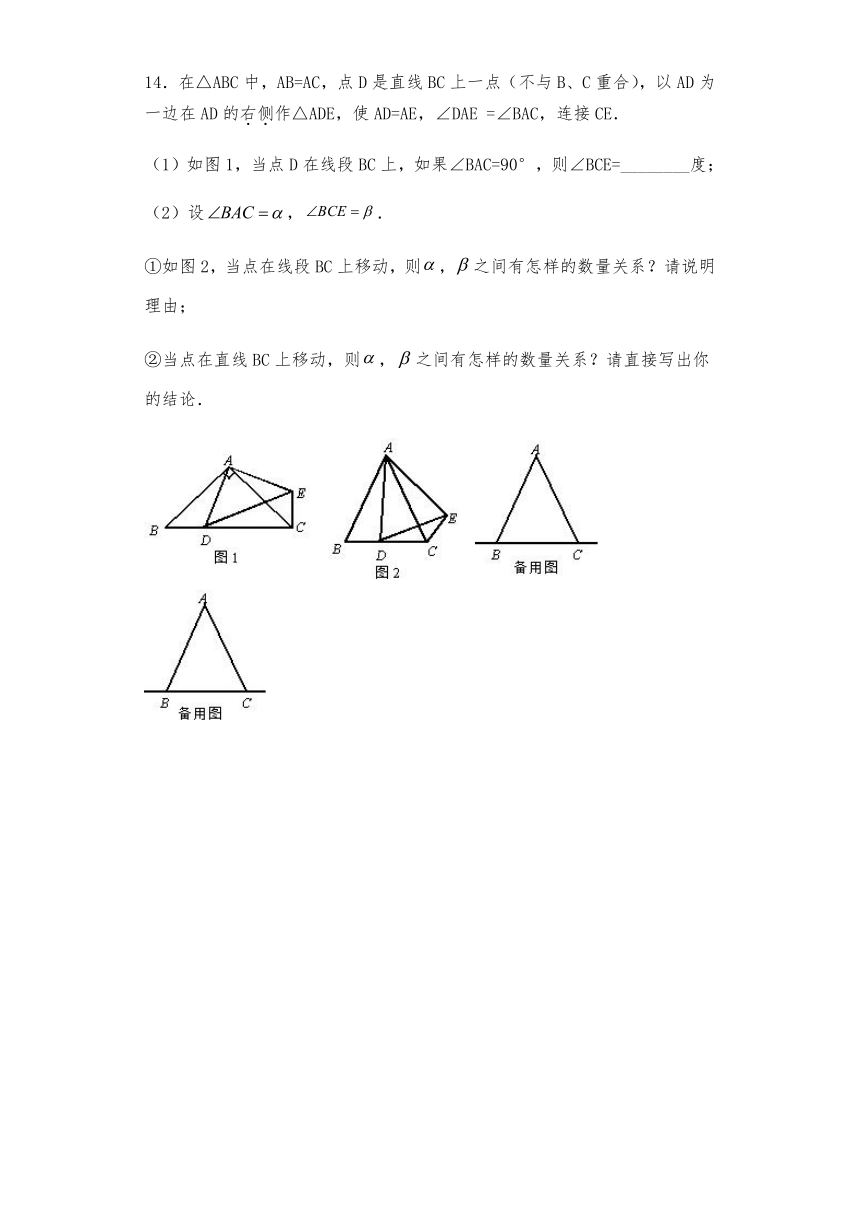
14.在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设,.
①如图2,当点在线段BC上移动,则,之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则,之间有怎样的数量关系?请直接写出你的结论.
第二课时
一、单选题
1.如图所示,Rt△ABE≌Rt△ECD,点B、E、C在同一直线上,则结论:①AE=ED;②AE⊥DE;③BC=AB+CD;④AB∥DC中成立的是( )
A.仅① B.仅①③ C.仅①③④ D.仅①②③④
2.三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数是( )
A. B. C. D.
3.如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,∠BAF=600,那么∠DAE等于( )
A.45° B.30 ° C.15° D.60°
4.中,厘米,,厘米,点D为AB的中点如果点P在线段BC上以v厘米秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动若点Q的运动速度为3厘米秒,则当与全等时,v的值为
A. B.3 C.或3 D.1或5
5.如图,在△ABC中,∠C=90°,AC=BC=,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( ).
A.1 B. C.2 D.
二、填空题
6.如图,△ABC中,AB=AC,AE=CF,BE=AF,则∠E=______,∠CAF=___.
7.如图所示,是将长方形纸牌ABCD沿着BD折叠得到的,图中包括实线、虚线在内共有全等三角形______ 对.
8.如图△ACB≌A′CB′,∠A′CB=30°,∠ACB′=110°,则∠ACA′的度数是________度.
9.如图,△ABC 中,点 A(0,1),点 C(4,3),如果要使△ABD 与△ABC 全等,那么符合条件的点 D 的坐标为___________.
三、解答题
10.如图所示,已知AE⊥AB,△ACE≌△AFB,CE、AB、BF分别交于点D、M.证明:CE⊥BF.
11.如图,在 ,,,分别过A、B作直线l的垂线,垂足分别为M、N.
(1)求证:≌;
(2)若,,求AB的长.
12.如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠C=∠E,DE=BC,AC=AE,求证:AD平分∠BDE.
13.已知,M是等边△ABC边BC上的点,如图,连接AM,过点M作∠AMH=60°,MH与∠ACB的邻补角的平分线交于点H,过H作HD⊥BC于点D
(1)求证:MA=MH
(2)猜想写出CB、CM、CD之间的数量关系式,并加以证明.
14.(背景)如图(a),△ABC与△ADE均是顶角为40°的等腰三角形,BC,DE分别是底边,求证:BD=CE.
(探究)如图(b),△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
①∠AEB的度数为________;②线段BE与AD之间的数量关系是________.
(拓展)如图(c),△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.
①求∠AEB的度数;
②请直接写出线段CM,AE,BE之间的数量关系.
第一课时答案
一、单选题
C.B.D.D.A.
二、填空题
6.3.
7.30°.
8.10
9.(﹣2,0).
三、解答题
10.∵ BE⊥AD,CF⊥AD
∴∠BED=∠CFD=90°,
∵点D是BC的中点
∴BD=CD
在△BDE和△CDF中
∴ △BDE≌△CDF (AAS)
11.
详解:∵∠ACB=90°,
∴∠1+∠2=90°.
∵AD⊥CE,BE⊥CE,
∴∠4=∠E=90°.
∴∠2+∠3=90°.
∴∠3=∠1.
又∵AC=BC.
∴△ACD≌△CBE.
∴BE=CD.
12.
∵AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=90°,∠AEF=90°,
∵∠AFE+∠CAD+∠AEF=180°,∠FBD+∠BFD+∠BDA=180°,∠AFE=∠BFD,
∴∠FBD=∠CAD,
∵在△BDF和△ADC中:,
∴△BDF≌△ADC(AAS),
∴BF=AC .
13.(1)∵△AOB,△COD是等腰直角三角形,
∴OC=OD,OA=OB,∠AOB=∠COD=90°,
∴∠AOC=∠BOD=90°﹣∠AOD,
在△AOC和△BOD中,
∴△AOC≌△BOD(SAS);
(2)∵△AOB,△COD是等腰直角三角形,
∴OC=OD,OA=OB,∠AOB=∠COD=90°,
∴∠B=∠OAB=45°,
∵△AOC≌△BOD,BD=1,
∴AC=BD=1,∠CAO=∠B=45°,
∵∠OAB=45°,
∴∠CAD=45°+45°=90°,
在Rt△CAD中,由勾股定理得:CD=.
14.(1);
(2)①.
理由:∵,
∴.
即.
又,
∴.
∴.
∴.
∴.
∵,
∴.
②当点在射线上时,.
当点在射线的反向延长线上时,.
第二课时答案
一、单选题
D.D.C.C.B.
二、填空题
6.∠F; ∠ABE
7.4
8.40
9.或或(-1,3)
三、解答题
10.
证明:∵AE⊥AB,
∴∠BAE=90°,
∵△ACE≌△AFB,
∴∠CAE=∠BAF,∠ACE=∠F,
∴∠CAB+∠BAE=∠BAC+∠CAF,
∴∠CAF=∠BAE=90°,
而∠ACE=∠F,
∴∠FMC=∠CAF=90°,
∴CE⊥BF.
11.
,,,
,
,,
,
在和中,
,
≌;
≌,
,
中,,
,,,
.
12.
证明:在△ABC和△ADE中,
,
∴△ABC≌△ADE,
∴AB=AD,∠ADE=∠B,
∴∠B=∠ADB,
∴∠ADB=∠ADE,
∴AD平分∠BDE.
13.(1)如图,过M点作MN∥AC交AB于N,
则BM=BN,∠ANM=120°,
∵AB=BC,
∴AN=MC,
∵CH是∠ACD的平分线,
∴∠ACH=60°=∠HCD,
∴∠MCH=∠ACB+∠ACH=120°,
又∵∠NMC=120°,∠AMH=60°,
∴∠HMC+∠AMN=60°
又∵∠NAM+∠AMN=∠BNM=60°,
∴∠HMC=∠MAN,
在△ANM和△MCH中,
,
∴△AMN≌△MHC(ASA),
∴MA=MH;
(2)CB=CM+2CD;
证明:如图,过M作MG⊥AB于G,
∵HD⊥BC,
∴∠HDC=∠MGB=90°,
∵△AMN≌△MHC,
∴MN=HC,
∵MN=MB,
∴HC=BM,
在△BMG和△CHD中,
,
∴△BMG≌△CHD(AAS),
∴CD=BG,
∵△BMN为等边三角形,
∴BM=2BG,
∴BM=2CD,
∴BC=MC+2CD.
14.
背景:∵∠BAC=∠DAE=40°,
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE,
在△BAD和△CAE中,,
∴△BAD≌△CAE,∴BD=CE;
探究:①∵△ACB和△DCE均为等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∠CDE=∠CED=60°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,,
∴△ACD≌△BCE,
∴∠ADC=∠BEC,
∵点A,D,E在同一直线上,
∴∠ADC=180-60=120°,
∴∠BEC=120°,
∴∠AEB=∠BEC-∠CED=120-60=60°,
故答案为:60°;
②∵△ACD≌△BCE,
∴BE=AD,
故答案为:BE=AD;
拓展:①∵△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,
∴AC=BC,CD=CE,∠CDE=∠CED=45°,
∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE,
∴AD=BE,∠ADC=∠BEC,
∵点A,D,E在同一直线上,
∴∠ADC=180°-∠CDE=180°-45°=135°,
∴∠BEC=135°,
∴∠AEB=∠BEC-∠CED=135°-45°=90°;
②∵∠DCE=90°,CD=CE,CM⊥DE,
∴CM=DM=EM,
∴DE=DM+EM=2CM,
又∵AD=BE,
∴AE=AD+DE=BE+2CM
第一课时
一、单选题
1.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
2.如图,△ABC≌△ADE,若∠E=70°,∠D=30°,∠CAD=35°,则∠BAD的度数为( )
A.40° B.45° C.50° D.55°
3.有下面的说法:①全等三角形的形状相同;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
4.如图,在中,分别是边上的点,若≌≌,则的度数为( )
A. B. C. D.
5.已知图中的两个三角形全等,则∠α的度数是( )
A.72° B.60° C.58° D.50°
二、填空题
6.如图,△ACE≌△DBF,点A、B、C、D共线,若AC=5,BC=2,则CD的长度等于________.
7.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为_______________°.
8.已知,且的周长为25,,则____________.
9.如图,在平面直角坐标系中,△AOB≌△COD,则点D的坐标是____________.
三、解答题
10.如图,在△ABC中,点D是BC边的中点,分别过点B、C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:≌.
11.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.求证:BE=CD.
12.如图,锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,DF=DC.
求证:BF=AC.
13.如图,△AOB,△COD是等腰直角三角形,点D在AB上,
(1)求证:△AOC≌△BOD;
(2)若AD=3,BD=1,求CD.
14.在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设,.
①如图2,当点在线段BC上移动,则,之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则,之间有怎样的数量关系?请直接写出你的结论.
第二课时
一、单选题
1.如图所示,Rt△ABE≌Rt△ECD,点B、E、C在同一直线上,则结论:①AE=ED;②AE⊥DE;③BC=AB+CD;④AB∥DC中成立的是( )
A.仅① B.仅①③ C.仅①③④ D.仅①②③④
2.三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数是( )
A. B. C. D.
3.如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,∠BAF=600,那么∠DAE等于( )
A.45° B.30 ° C.15° D.60°
4.中,厘米,,厘米,点D为AB的中点如果点P在线段BC上以v厘米秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动若点Q的运动速度为3厘米秒,则当与全等时,v的值为
A. B.3 C.或3 D.1或5
5.如图,在△ABC中,∠C=90°,AC=BC=,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( ).
A.1 B. C.2 D.
二、填空题
6.如图,△ABC中,AB=AC,AE=CF,BE=AF,则∠E=______,∠CAF=___.
7.如图所示,是将长方形纸牌ABCD沿着BD折叠得到的,图中包括实线、虚线在内共有全等三角形______ 对.
8.如图△ACB≌A′CB′,∠A′CB=30°,∠ACB′=110°,则∠ACA′的度数是________度.
9.如图,△ABC 中,点 A(0,1),点 C(4,3),如果要使△ABD 与△ABC 全等,那么符合条件的点 D 的坐标为___________.
三、解答题
10.如图所示,已知AE⊥AB,△ACE≌△AFB,CE、AB、BF分别交于点D、M.证明:CE⊥BF.
11.如图,在 ,,,分别过A、B作直线l的垂线,垂足分别为M、N.
(1)求证:≌;
(2)若,,求AB的长.
12.如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠C=∠E,DE=BC,AC=AE,求证:AD平分∠BDE.
13.已知,M是等边△ABC边BC上的点,如图,连接AM,过点M作∠AMH=60°,MH与∠ACB的邻补角的平分线交于点H,过H作HD⊥BC于点D
(1)求证:MA=MH
(2)猜想写出CB、CM、CD之间的数量关系式,并加以证明.
14.(背景)如图(a),△ABC与△ADE均是顶角为40°的等腰三角形,BC,DE分别是底边,求证:BD=CE.
(探究)如图(b),△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
①∠AEB的度数为________;②线段BE与AD之间的数量关系是________.
(拓展)如图(c),△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.
①求∠AEB的度数;
②请直接写出线段CM,AE,BE之间的数量关系.
第一课时答案
一、单选题
C.B.D.D.A.
二、填空题
6.3.
7.30°.
8.10
9.(﹣2,0).
三、解答题
10.∵ BE⊥AD,CF⊥AD
∴∠BED=∠CFD=90°,
∵点D是BC的中点
∴BD=CD
在△BDE和△CDF中
∴ △BDE≌△CDF (AAS)
11.
详解:∵∠ACB=90°,
∴∠1+∠2=90°.
∵AD⊥CE,BE⊥CE,
∴∠4=∠E=90°.
∴∠2+∠3=90°.
∴∠3=∠1.
又∵AC=BC.
∴△ACD≌△CBE.
∴BE=CD.
12.
∵AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=90°,∠AEF=90°,
∵∠AFE+∠CAD+∠AEF=180°,∠FBD+∠BFD+∠BDA=180°,∠AFE=∠BFD,
∴∠FBD=∠CAD,
∵在△BDF和△ADC中:,
∴△BDF≌△ADC(AAS),
∴BF=AC .
13.(1)∵△AOB,△COD是等腰直角三角形,
∴OC=OD,OA=OB,∠AOB=∠COD=90°,
∴∠AOC=∠BOD=90°﹣∠AOD,
在△AOC和△BOD中,
∴△AOC≌△BOD(SAS);
(2)∵△AOB,△COD是等腰直角三角形,
∴OC=OD,OA=OB,∠AOB=∠COD=90°,
∴∠B=∠OAB=45°,
∵△AOC≌△BOD,BD=1,
∴AC=BD=1,∠CAO=∠B=45°,
∵∠OAB=45°,
∴∠CAD=45°+45°=90°,
在Rt△CAD中,由勾股定理得:CD=.
14.(1);
(2)①.
理由:∵,
∴.
即.
又,
∴.
∴.
∴.
∴.
∵,
∴.
②当点在射线上时,.
当点在射线的反向延长线上时,.
第二课时答案
一、单选题
D.D.C.C.B.
二、填空题
6.∠F; ∠ABE
7.4
8.40
9.或或(-1,3)
三、解答题
10.
证明:∵AE⊥AB,
∴∠BAE=90°,
∵△ACE≌△AFB,
∴∠CAE=∠BAF,∠ACE=∠F,
∴∠CAB+∠BAE=∠BAC+∠CAF,
∴∠CAF=∠BAE=90°,
而∠ACE=∠F,
∴∠FMC=∠CAF=90°,
∴CE⊥BF.
11.
,,,
,
,,
,
在和中,
,
≌;
≌,
,
中,,
,,,
.
12.
证明:在△ABC和△ADE中,
,
∴△ABC≌△ADE,
∴AB=AD,∠ADE=∠B,
∴∠B=∠ADB,
∴∠ADB=∠ADE,
∴AD平分∠BDE.
13.(1)如图,过M点作MN∥AC交AB于N,
则BM=BN,∠ANM=120°,
∵AB=BC,
∴AN=MC,
∵CH是∠ACD的平分线,
∴∠ACH=60°=∠HCD,
∴∠MCH=∠ACB+∠ACH=120°,
又∵∠NMC=120°,∠AMH=60°,
∴∠HMC+∠AMN=60°
又∵∠NAM+∠AMN=∠BNM=60°,
∴∠HMC=∠MAN,
在△ANM和△MCH中,
,
∴△AMN≌△MHC(ASA),
∴MA=MH;
(2)CB=CM+2CD;
证明:如图,过M作MG⊥AB于G,
∵HD⊥BC,
∴∠HDC=∠MGB=90°,
∵△AMN≌△MHC,
∴MN=HC,
∵MN=MB,
∴HC=BM,
在△BMG和△CHD中,
,
∴△BMG≌△CHD(AAS),
∴CD=BG,
∵△BMN为等边三角形,
∴BM=2BG,
∴BM=2CD,
∴BC=MC+2CD.
14.
背景:∵∠BAC=∠DAE=40°,
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE,
在△BAD和△CAE中,,
∴△BAD≌△CAE,∴BD=CE;
探究:①∵△ACB和△DCE均为等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∠CDE=∠CED=60°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,,
∴△ACD≌△BCE,
∴∠ADC=∠BEC,
∵点A,D,E在同一直线上,
∴∠ADC=180-60=120°,
∴∠BEC=120°,
∴∠AEB=∠BEC-∠CED=120-60=60°,
故答案为:60°;
②∵△ACD≌△BCE,
∴BE=AD,
故答案为:BE=AD;
拓展:①∵△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,
∴AC=BC,CD=CE,∠CDE=∠CED=45°,
∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE,
∴AD=BE,∠ADC=∠BEC,
∵点A,D,E在同一直线上,
∴∠ADC=180°-∠CDE=180°-45°=135°,
∴∠BEC=135°,
∴∠AEB=∠BEC-∠CED=135°-45°=90°;
②∵∠DCE=90°,CD=CE,CM⊥DE,
∴CM=DM=EM,
∴DE=DM+EM=2CM,
又∵AD=BE,
∴AE=AD+DE=BE+2CM
