八年级数学上册试题 14.2三角形全等的判定同步练习-沪科版(含答案)
文档属性
| 名称 | 八年级数学上册试题 14.2三角形全等的判定同步练习-沪科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 455.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 19:23:02 | ||
图片预览


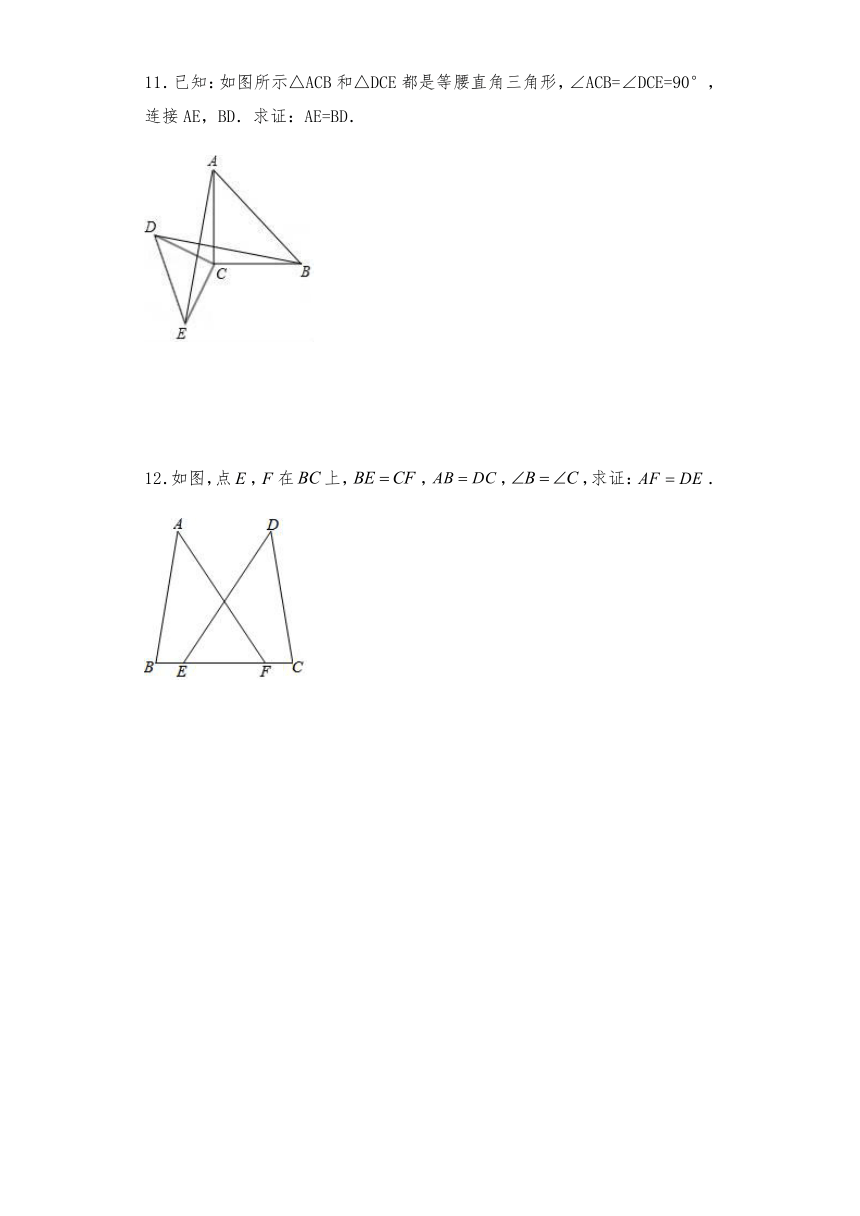
文档简介
14.2三角形全等的判定
第一课时
一、单选题
1.尺规作图作的平分线方法如下:以为圆心,任意长为半径画弧交、于、,再分别以点、为圆心,以大于长为半径画弧,两弧交于点,作射线由作法得的根据是( )
A.SAS B.ASA C.AAS D.SSS
2.如图,△ABC中,∠A=90°,AB=AC,BD平分∠ABE,DE⊥BC,如果BC=10 cm,则△DEC的周长是( )
A.8 cm B.10 cm C.11 cm D.12 cm
3.如图,PD⊥AB,PE⊥AC,垂足分别为D、E,且PA平分∠BAC,则△APD与△APE全等的理由是( )
A.SAS B.AAS C.SSS D.ASA
4.如图所示,点E在△ABC外部,点D在BC边上,DE交AC于点F.若∠1=∠2,∠E=∠C,AE=AC,则( )
A.△ABC≌△AFE B.△AFE≌△ADC
C.△AFE≌△DFC D.△ABC≌△ADE
5.如图,AB⊥BC,DC⊥BC,AE 平分∠BAD,DE 平分∠ADC,以下结论:①∠AED=90°;②点 E 是 BC 的中点;③DE=BE;④AD=AB+CD;其中正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题
6.如图,在△ABD和△ACE中,有下列四个判断:①AB=AC;②AD=AE;③∠B=∠C;④BD=CE,请以其中三个判断为条件,另一个为结果,写出一个正确的结论______________________(用序号 形式写出).
7.如图,B,C,D,E在一条直线上,且BC=DE,AC=FD,AE=FB,则△ACE≌_____,理由是_____________,∠ACE=________,理由是___________.
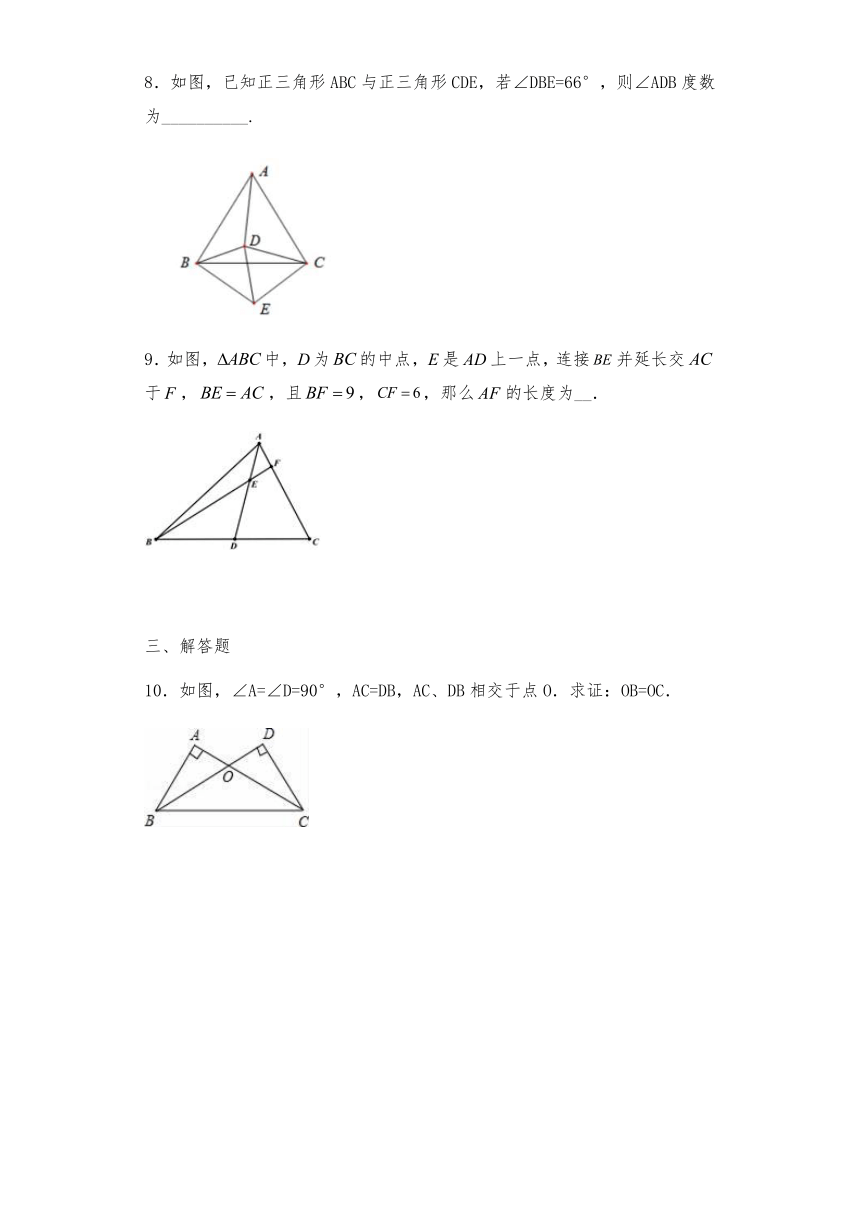
8.如图,已知正三角形ABC与正三角形CDE,若∠DBE=66°,则∠ADB度数为__________.
9.如图,中,为的中点,是上一点,连接并延长交于,,且,,那么的长度为__.
三、解答题
10.如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:OB=OC.
11.已知:如图所示△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AE,BD.求证:AE=BD.
12.如图,点,在上,,,,求证:.
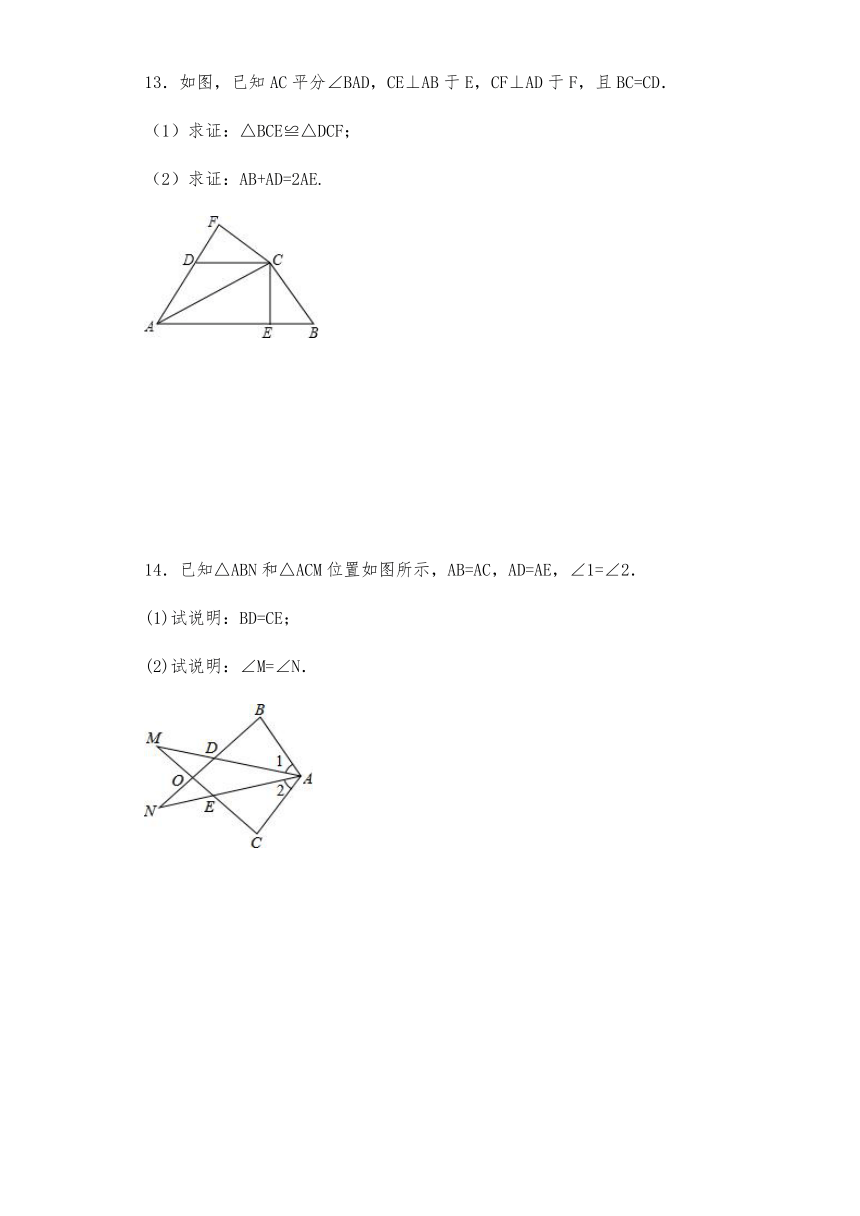
13.如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△BCE≌△DCF;
(2)求证:AB+AD=2AE.
14.已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
(1)试说明:BD=CE;
(2)试说明:∠M=∠N.
第二课时
一、单选题
1.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙
2.如图,,且.、是上两点,,.若,,,则的长为( )
A. B. C. D.
3.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
A.1个 B.2个 C.3个 D.4个
4.如图,等边三角形ABC边长是定值,点O是它的外心,过点O任意作一条直线分别交AB,BC于点D,E,将△BDE沿直线DE折叠,得到△B′DE,若B′D,B′E分别交AC于点F,G,连接OF,OG,则下列判断错误的是( )
A.△ADF≌△CGE
B.△B′FG的周长是一个定值
C.四边形FOEC的面积是一个定值
D.四边形OGB'F的面积是一个定值
5.如图,已知在正方形中,点分别在上,△是等边三角形,连接交于,给出下列结论:
①; ② ;
③垂直平分; ④.
其中结论正确的共有( ).
A.1个 B.2个 C.3个 D.4个
二、填空题
6.如图,AC=DC,BC=EC,请你添加一个适当的条件:______________,使得△ABC≌△DEC.
7.已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正确的结论有________(填序号).
8.如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,BF = CE,AC∥DF,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是 .(只需写一个,不添加辅助线)
9.如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE中点,连接MD,若BD=2,CD=1.则MD的长为______ .
三、解答题
10.已知:如图,点A、D、C、B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:AE∥BF.
11.如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:
(1)△AEF≌△CEB;
(2)AF=2CD.
12.如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
13.已知△ABC和△ADE都是等腰直角三角形,点D是直线BC上的一动点(点D不与B、C重合),连接CE,
(1)在图1中,当点D在边BC上时,求证:BC=CE+CD;
(2)在图2中,当点D在边BC的延长线上时,结论BC=CE+CD是否还成立?若不成立,请猜想BC、CE、CD之间存在的数量关系,并说明理由;
(3)在图3中,当点D在边BC的反向延长线上时,补全图形,不需写证明过程,直接写出BC、CE、CD之间存在的数量关系.
14.如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.
第一课时答案
一、单选题
D.B.B.D.B.
二、填空题
6.①②④ ③或①③④ ②;
7.△FDB SSS ∠FDB 全等三角形的对应角相等
8.126°
9.;
三、解答题
10.证明:在Rt△ABC和Rt△DCB中
,
∴Rt△ABC≌Rt△DCB(HL),
∴∠OBC=∠OCB,
∴BO=CO.
11.
证明:∵△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,
∴AC=BC,DC=EC,
∴∠ACB+∠ACD=∠DCE+∠ACD,
∴∠BCD=∠ACE,
在△ACE与△BCD中,
,
∴△ACE≌△BCD(SAS),
∴AE=BD.
12.
证明:∵,
∴,即,
在和中,
,
∴≌
∴.
13.
(1)证明:∵AC是角平分线,CE⊥AB于E,CF⊥AD于F,
∴CE=CF,∠F=∠CEB=90°,
在Rt△BCE和Rt△DCF中,
∴△BCE≌△DCF;
(2)解:∵CE⊥AB于E,CF⊥AD于F,
∴∠F=∠CEA=90°,
在Rt△FAC和Rt△EAC中,,
∴Rt△FAC≌Rt△EAC,
∴AF=AE,
∵△BCE≌△DCF,
∴BE=DF,
∴AB+AD=(AE+BE)+(AF﹣DF)=AE+BE+AE﹣DF=2AE.
14.
(1)在△ADB和△AEC中,
∴△ADB≌△AEC
∴BD=CE
(2)∵
∴
即
又△ADB≌△AEC
∴180°-
即.
第二课时答案
一、单选题
B.D.C. D.C
二、填空题
6.CE=BC.本题答案不唯一.
7.①②④
8.AC=DF(答案不唯一)
9.
三、解答题
10.证明:∵AD=BC,∴AC=BD,
在△ACE和△BDF中,
,
∴△ACE≌△BDF(SSS)
∴∠A=∠B,
∴AE∥BF;
11.
(1)证明:由于AB=AC,故△ABC为等腰三角形,∠ABC=∠ACB;
∵AD⊥BC,CE⊥AB,
∴∠AEC=∠BEC=90°,∠ADB=90°;
∴∠BAD+∠ABC=90°,∠ECB+∠ABC=90°,
∴∠BAD=∠ECB,
在Rt△AEF和Rt△CEB中
∠AEF=∠CEB,AE=CE,∠EAF=∠ECB,
所以△AEF≌△CEB(ASA)
(2)∵△ABC为等腰三角形,AD⊥BC,
故BD=CD,
即CB=2CD,
又∵△AEF≌△CEB,
∴AF=CB=2CD.
12.
(1)证明:连接AD
∵,为边的中点
∴AD平分∠BAC
∵DE⊥AB于点E, DF⊥AC于点F
∴DE=DF
(2)解:,,
∴△ABC为等边三角形.
∴,
,
∴,
∴BE=BD,
,∴BD=2,∴BC=2BD=4,
∴的周长为12
13.
(1)如图1中,
∵AB=AC,∠ABC=∠ACB=45°,AD=AE,∠ADE=∠AED=45°,
∴∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴BC=BD+CD=CE+CD;
(2)不成立,存在的数量关系为CE=BC+CD.
理由:如图2,由(1)同理可得,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴BD=BC+CD,
∴CE=BC+CD;
(3)如图3,结论:CD=BC+EC.
理由:由(1)同理可得,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴CD=BC+BD=BC+CE,
14.
证明:
在△ABC和△DEC中,,
(2)∵∠ACD=90°,AC=CD,
∴∠1=∠D=45°,
∵AE=AC,
∴∠3=∠5=67.5°,
∴∠DEC=180°-∠5=112.5°.
第一课时
一、单选题
1.尺规作图作的平分线方法如下:以为圆心,任意长为半径画弧交、于、,再分别以点、为圆心,以大于长为半径画弧,两弧交于点,作射线由作法得的根据是( )
A.SAS B.ASA C.AAS D.SSS
2.如图,△ABC中,∠A=90°,AB=AC,BD平分∠ABE,DE⊥BC,如果BC=10 cm,则△DEC的周长是( )
A.8 cm B.10 cm C.11 cm D.12 cm
3.如图,PD⊥AB,PE⊥AC,垂足分别为D、E,且PA平分∠BAC,则△APD与△APE全等的理由是( )
A.SAS B.AAS C.SSS D.ASA
4.如图所示,点E在△ABC外部,点D在BC边上,DE交AC于点F.若∠1=∠2,∠E=∠C,AE=AC,则( )
A.△ABC≌△AFE B.△AFE≌△ADC
C.△AFE≌△DFC D.△ABC≌△ADE
5.如图,AB⊥BC,DC⊥BC,AE 平分∠BAD,DE 平分∠ADC,以下结论:①∠AED=90°;②点 E 是 BC 的中点;③DE=BE;④AD=AB+CD;其中正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题
6.如图,在△ABD和△ACE中,有下列四个判断:①AB=AC;②AD=AE;③∠B=∠C;④BD=CE,请以其中三个判断为条件,另一个为结果,写出一个正确的结论______________________(用序号 形式写出).
7.如图,B,C,D,E在一条直线上,且BC=DE,AC=FD,AE=FB,则△ACE≌_____,理由是_____________,∠ACE=________,理由是___________.
8.如图,已知正三角形ABC与正三角形CDE,若∠DBE=66°,则∠ADB度数为__________.
9.如图,中,为的中点,是上一点,连接并延长交于,,且,,那么的长度为__.
三、解答题
10.如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:OB=OC.
11.已知:如图所示△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AE,BD.求证:AE=BD.
12.如图,点,在上,,,,求证:.
13.如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△BCE≌△DCF;
(2)求证:AB+AD=2AE.
14.已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
(1)试说明:BD=CE;
(2)试说明:∠M=∠N.
第二课时
一、单选题
1.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙
2.如图,,且.、是上两点,,.若,,,则的长为( )
A. B. C. D.
3.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
A.1个 B.2个 C.3个 D.4个
4.如图,等边三角形ABC边长是定值,点O是它的外心,过点O任意作一条直线分别交AB,BC于点D,E,将△BDE沿直线DE折叠,得到△B′DE,若B′D,B′E分别交AC于点F,G,连接OF,OG,则下列判断错误的是( )
A.△ADF≌△CGE
B.△B′FG的周长是一个定值
C.四边形FOEC的面积是一个定值
D.四边形OGB'F的面积是一个定值
5.如图,已知在正方形中,点分别在上,△是等边三角形,连接交于,给出下列结论:
①; ② ;
③垂直平分; ④.
其中结论正确的共有( ).
A.1个 B.2个 C.3个 D.4个
二、填空题
6.如图,AC=DC,BC=EC,请你添加一个适当的条件:______________,使得△ABC≌△DEC.
7.已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正确的结论有________(填序号).
8.如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,BF = CE,AC∥DF,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是 .(只需写一个,不添加辅助线)
9.如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE中点,连接MD,若BD=2,CD=1.则MD的长为______ .
三、解答题
10.已知:如图,点A、D、C、B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:AE∥BF.
11.如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:
(1)△AEF≌△CEB;
(2)AF=2CD.
12.如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
13.已知△ABC和△ADE都是等腰直角三角形,点D是直线BC上的一动点(点D不与B、C重合),连接CE,
(1)在图1中,当点D在边BC上时,求证:BC=CE+CD;
(2)在图2中,当点D在边BC的延长线上时,结论BC=CE+CD是否还成立?若不成立,请猜想BC、CE、CD之间存在的数量关系,并说明理由;
(3)在图3中,当点D在边BC的反向延长线上时,补全图形,不需写证明过程,直接写出BC、CE、CD之间存在的数量关系.
14.如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.
第一课时答案
一、单选题
D.B.B.D.B.
二、填空题
6.①②④ ③或①③④ ②;
7.△FDB SSS ∠FDB 全等三角形的对应角相等
8.126°
9.;
三、解答题
10.证明:在Rt△ABC和Rt△DCB中
,
∴Rt△ABC≌Rt△DCB(HL),
∴∠OBC=∠OCB,
∴BO=CO.
11.
证明:∵△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,
∴AC=BC,DC=EC,
∴∠ACB+∠ACD=∠DCE+∠ACD,
∴∠BCD=∠ACE,
在△ACE与△BCD中,
,
∴△ACE≌△BCD(SAS),
∴AE=BD.
12.
证明:∵,
∴,即,
在和中,
,
∴≌
∴.
13.
(1)证明:∵AC是角平分线,CE⊥AB于E,CF⊥AD于F,
∴CE=CF,∠F=∠CEB=90°,
在Rt△BCE和Rt△DCF中,
∴△BCE≌△DCF;
(2)解:∵CE⊥AB于E,CF⊥AD于F,
∴∠F=∠CEA=90°,
在Rt△FAC和Rt△EAC中,,
∴Rt△FAC≌Rt△EAC,
∴AF=AE,
∵△BCE≌△DCF,
∴BE=DF,
∴AB+AD=(AE+BE)+(AF﹣DF)=AE+BE+AE﹣DF=2AE.
14.
(1)在△ADB和△AEC中,
∴△ADB≌△AEC
∴BD=CE
(2)∵
∴
即
又△ADB≌△AEC
∴180°-
即.
第二课时答案
一、单选题
B.D.C. D.C
二、填空题
6.CE=BC.本题答案不唯一.
7.①②④
8.AC=DF(答案不唯一)
9.
三、解答题
10.证明:∵AD=BC,∴AC=BD,
在△ACE和△BDF中,
,
∴△ACE≌△BDF(SSS)
∴∠A=∠B,
∴AE∥BF;
11.
(1)证明:由于AB=AC,故△ABC为等腰三角形,∠ABC=∠ACB;
∵AD⊥BC,CE⊥AB,
∴∠AEC=∠BEC=90°,∠ADB=90°;
∴∠BAD+∠ABC=90°,∠ECB+∠ABC=90°,
∴∠BAD=∠ECB,
在Rt△AEF和Rt△CEB中
∠AEF=∠CEB,AE=CE,∠EAF=∠ECB,
所以△AEF≌△CEB(ASA)
(2)∵△ABC为等腰三角形,AD⊥BC,
故BD=CD,
即CB=2CD,
又∵△AEF≌△CEB,
∴AF=CB=2CD.
12.
(1)证明:连接AD
∵,为边的中点
∴AD平分∠BAC
∵DE⊥AB于点E, DF⊥AC于点F
∴DE=DF
(2)解:,,
∴△ABC为等边三角形.
∴,
,
∴,
∴BE=BD,
,∴BD=2,∴BC=2BD=4,
∴的周长为12
13.
(1)如图1中,
∵AB=AC,∠ABC=∠ACB=45°,AD=AE,∠ADE=∠AED=45°,
∴∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴BC=BD+CD=CE+CD;
(2)不成立,存在的数量关系为CE=BC+CD.
理由:如图2,由(1)同理可得,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴BD=BC+CD,
∴CE=BC+CD;
(3)如图3,结论:CD=BC+EC.
理由:由(1)同理可得,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴CD=BC+BD=BC+CE,
14.
证明:
在△ABC和△DEC中,,
(2)∵∠ACD=90°,AC=CD,
∴∠1=∠D=45°,
∵AE=AC,
∴∠3=∠5=67.5°,
∴∠DEC=180°-∠5=112.5°.
