八年级数学沪科版上册试题 15.1轴对称图形同步练习(1-2课时) (含答案)
文档属性
| 名称 | 八年级数学沪科版上册试题 15.1轴对称图形同步练习(1-2课时) (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 424.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 00:00:00 | ||
图片预览



文档简介
15.1轴对称图形
第一课时
一、单选题
1.如图,ABCD为一长方形纸带,AB∥CD,将ABCD沿EF折,A、D两点分别与对应,若∠1=2∠2,则∠AEF的度数为
A.60° B.65° C.72° D.75°
2.下面四个手机应用图标中是轴对称图形的是( )
A. B. C. D.
3.如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( )
A.35° B.40° C.45° D.50°
4.若点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,则m+n的值是( )
A.﹣5 B.﹣3 C.3 D.1
5.如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠DOF=142°,则∠C的度数为( )
A.38° B.39° C.42° D.48°
二、填空题
6.已知点P(3,a)关于y轴的对称点为Q(b,2),则ab=_____.
7.如图,在中,,,,点、分别在、上,且和关于对称,则的周长为__.
8.如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知AC=5 cm,△ADC的周长为17 cm,则BC的长为________.
9.将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕,若∠ABE=20°,则∠DBC为_____度.
三、解答题
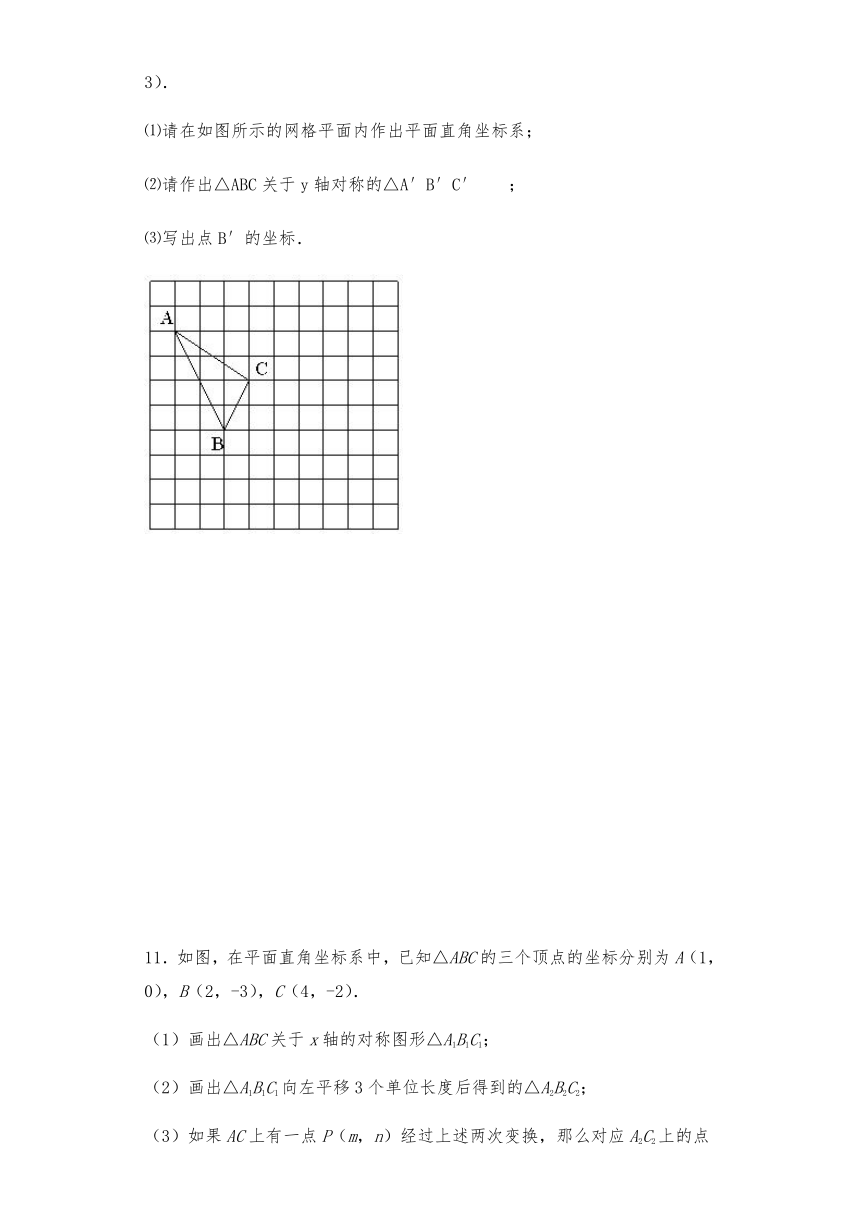
10.在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(,5),(,3).
⑴请在如图所示的网格平面内作出平面直角坐标系;
⑵请作出△ABC关于y轴对称的△A′B′C′;
⑶写出点B′的坐标.
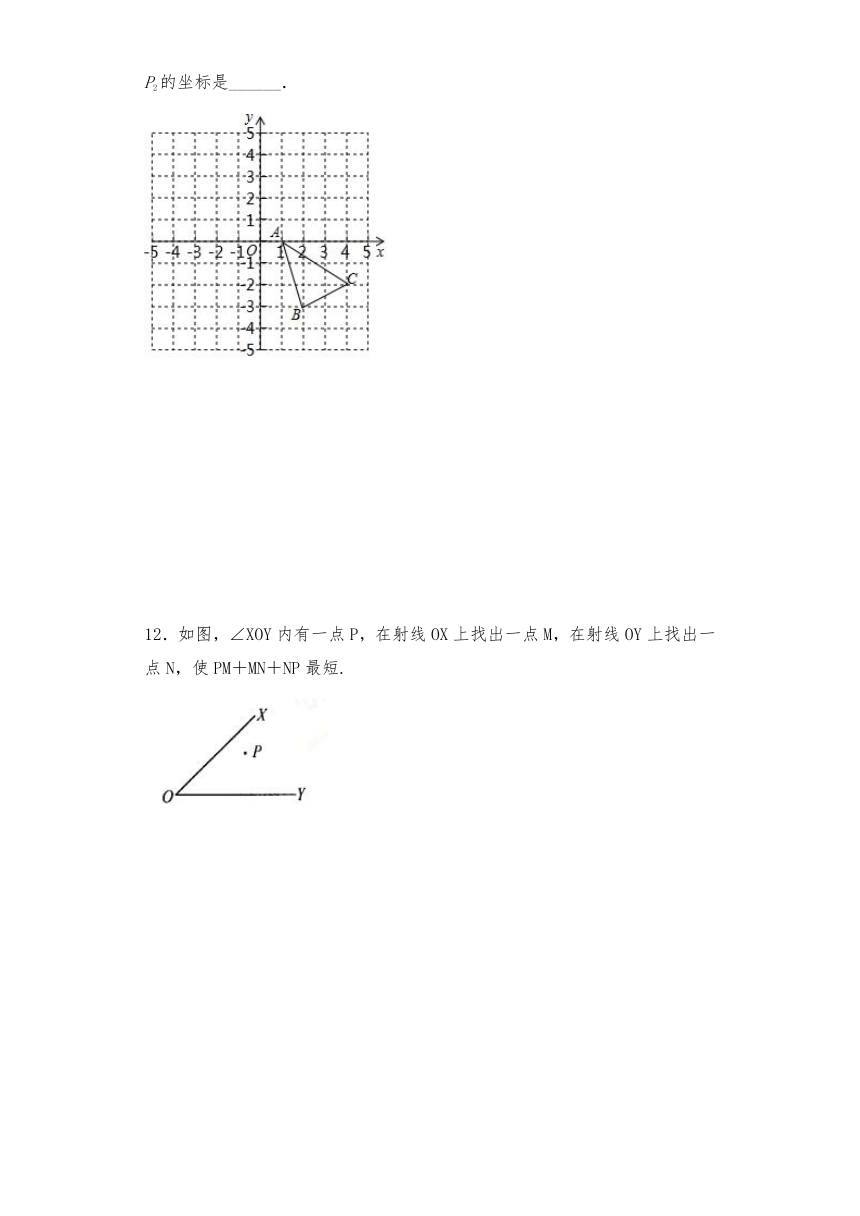
11.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(1,0),B(2,-3),C(4,-2).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1向左平移3个单位长度后得到的△A2B2C2;
(3)如果AC上有一点P(m,n)经过上述两次变换,那么对应A2C2上的点P2的坐标是______.
12.如图,∠XOY内有一点P,在射线OX上找出一点M,在射线OY上找出一点N,使PM+MN+NP最短.
13.如图,∠A=90°,E为BC上一点,A点和E点关于BD对称,B点、C点关于DE对称,求∠ABC和∠C的度数.
14.如图,在△ABC中,AB=AC,D、E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′;
(1)求证:△ABD≌△ACD′;
(2)若∠BAC=120°,求∠DAE的度数.
第二课时
一、单选题
1.如图,将 ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为( )
A.66° B.104° C.114° D.124°
2.下列图形中,不是轴对称图形的是( )
A. B. C. D.
3.在平面直角坐标系中.点P(1,﹣2)关于x轴的对称点的坐标是( )
A.(1,2) B.(﹣1,﹣2) C.(﹣1,2) D.(﹣2,1)
4.如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
A.130° B.120° C.110° D.100°
5.如图,BD是△ABC的角平分线,DE∥BC,DE交AB于E,若AB=BC,则下列结论中错误的是( )
A.BD⊥AC B.∠A=∠EDA C.2AD=BC D.BE=ED
二、填空题
6.把一张对边互相平行的纸条(AC′//BD′)折成如图所示,EF是折痕,若折痕EF与一边的夹角∠EFB=32°,则∠AEG=____.
7.如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有______种.
8.已知坐标平面内一点A(1,-2)
(1)若A、B两点关于x轴对称,则B(________),
(2)若A、B两点关于y轴对称,则B(________),
(3)若A、B两点关于原点对称,则B(________).
9.如图,在中,点A的坐标为,点B的坐标为,点C的坐标为,点D在第二象限,且与全等,点D的坐标是______.
三、解答题
10.下图,要在燃气管道L上修建一个泵站,分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?(不写做法,保留作图痕迹)
11.如图,在正方形网格上有一个△ABC.
(1)画出△ABC关于直线MN的对称图形(不写画法);
(2)若网格上的每个小正方形的边长为1,求△ABC的面积.
12.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),
C(3,4)
⑴ 作出与△ABC关于y轴对称△A1B1C1,并写出 三个顶点的坐标为:A1( ),B1( ),C1( );
⑵ 在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标;
⑶ 在 y 轴上是否存在点 Q,使得S△AOQ=S△ABC,如果存在,求出点 Q 的坐标,如果不存在,说明理由。
13.已知点A(2a-b,5+a),B(2b-1,-a+b).
(1)若点A、B关于x轴对称,求a、b的值;
(2)若A、B关于y轴对称,求﹙4a+b﹚2014的值.
14.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)若△A1B1C1与△ABC关于y轴成轴对称,则△A1B1C1三个顶点坐标分别为A1_____,B1_____,C1_____
(2)在y轴上是否存在点Q.使得S△ACQ=S△ABC,如果存在,求出点Q的坐标,如果不存在,说明理由;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标是_____.
第一课时答案
一、单选题
C.D.A.D.A.
二、填空题
6.-6.
7.8.
8.12cm.
9.70.
三、解答题
10.
解:
(1)如图;
(2)如图;
(3)点B′的坐标为(2,1).
11.
(1)解:如图所示:△A1B1C1就是所要求作的图形、
(2)△A2B2C2就是所要求作的图形;
(3)如果AC上有一点P(m,n)经过上述两次变换,那么对应A2C2上的点P2的坐标是:
故答案为(m 3, n).
12.
解:如图所示,分别以直线OX、OY为对称轴,作点P的对称点与,
连接,分别交OX于点M,交OY于点N,则PM+MN+NP最短.
13.
∵A点和E点关于BD对称,
∴∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD.
又B点、C点关于DE对称,
∴∠DBE=∠C,∠ABC=2∠C.
∵∠A=90°,∴∠ABC+∠C=2∠C+∠C=3∠C=90°.
∴∠C=30°,
∴∠ABC=2∠C=60°.
14.
()证明:∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
∴,
在△ABD和△ACD′中,
∵ ,
∴ △ABD≌△ACD′(SSS).
()解:∵≌,
∴,
∴,
∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
∴,
即.
第二课时答案
一、单选题
C.A.A.B.C
二、填空题
6.116°
7.3.
8.(1,2)、(-1,-2)、(-1,2)
9.(-4,2)或(-4,3)
三、解答题
10.作点A关于燃气管道的对称点A′,连接A′B交燃气管道于点P,即点P即为所求.
11.(1)如图所示:
(2)S=5×4-×4×1-×4×1-×5×3=8.5.
12.(1)△A1B1C1如图所示,A1(-1,1),B1(-4,2),C1(-3,4);
(2)如图1,找出A的对称点A′(1,﹣1),连接BA′,与x轴交点即为P,点P坐标为(2,0);
(3)设存在点 Q,使得S△AOQ=S△ABC,如图2,作AD⊥y轴于D,设Q点坐标为(0,y),则 OQ=|y|,AD=1,
S△ABC==,
由题意,S△AOQ=S△ABC,得 ,
或,
∴ Q点坐标为(0,)或(0,).
13.
解:(1)∵点A,B关于x轴对称,
∴,
解得;
(2)∵A,B关于y轴对称,
∴,
解得,
所以(4a+b)2016=[4×(-1)+3]2016=1.
14.
(1)△A1B1C1如图所示,A1(﹣1,1),B1(﹣4,2),C1(﹣3,4).
故答案为(﹣1,1),(﹣4,2),(﹣3,4).
(2)存在.设Q(0,m),
∵S△ABC=9﹣×2×3﹣×3×1﹣×1×2=,
∴S△QAC=,
∴|m| 3﹣ |m| 1=,
∴m=±,
∴Q(0,)或(0,﹣).
(3)如图作点B关于x轴的对称点B′,连接AB′交x轴于P,此时PA+PB的值最小,此时P(2,0).
第一课时
一、单选题
1.如图,ABCD为一长方形纸带,AB∥CD,将ABCD沿EF折,A、D两点分别与对应,若∠1=2∠2,则∠AEF的度数为
A.60° B.65° C.72° D.75°
2.下面四个手机应用图标中是轴对称图形的是( )
A. B. C. D.
3.如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( )
A.35° B.40° C.45° D.50°
4.若点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,则m+n的值是( )
A.﹣5 B.﹣3 C.3 D.1
5.如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠DOF=142°,则∠C的度数为( )
A.38° B.39° C.42° D.48°
二、填空题
6.已知点P(3,a)关于y轴的对称点为Q(b,2),则ab=_____.
7.如图,在中,,,,点、分别在、上,且和关于对称,则的周长为__.
8.如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知AC=5 cm,△ADC的周长为17 cm,则BC的长为________.
9.将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕,若∠ABE=20°,则∠DBC为_____度.
三、解答题
10.在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(,5),(,3).
⑴请在如图所示的网格平面内作出平面直角坐标系;
⑵请作出△ABC关于y轴对称的△A′B′C′;
⑶写出点B′的坐标.
11.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(1,0),B(2,-3),C(4,-2).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1向左平移3个单位长度后得到的△A2B2C2;
(3)如果AC上有一点P(m,n)经过上述两次变换,那么对应A2C2上的点P2的坐标是______.
12.如图,∠XOY内有一点P,在射线OX上找出一点M,在射线OY上找出一点N,使PM+MN+NP最短.
13.如图,∠A=90°,E为BC上一点,A点和E点关于BD对称,B点、C点关于DE对称,求∠ABC和∠C的度数.
14.如图,在△ABC中,AB=AC,D、E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′;
(1)求证:△ABD≌△ACD′;
(2)若∠BAC=120°,求∠DAE的度数.
第二课时
一、单选题
1.如图,将 ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为( )
A.66° B.104° C.114° D.124°
2.下列图形中,不是轴对称图形的是( )
A. B. C. D.
3.在平面直角坐标系中.点P(1,﹣2)关于x轴的对称点的坐标是( )
A.(1,2) B.(﹣1,﹣2) C.(﹣1,2) D.(﹣2,1)
4.如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
A.130° B.120° C.110° D.100°
5.如图,BD是△ABC的角平分线,DE∥BC,DE交AB于E,若AB=BC,则下列结论中错误的是( )
A.BD⊥AC B.∠A=∠EDA C.2AD=BC D.BE=ED
二、填空题
6.把一张对边互相平行的纸条(AC′//BD′)折成如图所示,EF是折痕,若折痕EF与一边的夹角∠EFB=32°,则∠AEG=____.
7.如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有______种.
8.已知坐标平面内一点A(1,-2)
(1)若A、B两点关于x轴对称,则B(________),
(2)若A、B两点关于y轴对称,则B(________),
(3)若A、B两点关于原点对称,则B(________).
9.如图,在中,点A的坐标为,点B的坐标为,点C的坐标为,点D在第二象限,且与全等,点D的坐标是______.
三、解答题
10.下图,要在燃气管道L上修建一个泵站,分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?(不写做法,保留作图痕迹)
11.如图,在正方形网格上有一个△ABC.
(1)画出△ABC关于直线MN的对称图形(不写画法);
(2)若网格上的每个小正方形的边长为1,求△ABC的面积.
12.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),
C(3,4)
⑴ 作出与△ABC关于y轴对称△A1B1C1,并写出 三个顶点的坐标为:A1( ),B1( ),C1( );
⑵ 在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标;
⑶ 在 y 轴上是否存在点 Q,使得S△AOQ=S△ABC,如果存在,求出点 Q 的坐标,如果不存在,说明理由。
13.已知点A(2a-b,5+a),B(2b-1,-a+b).
(1)若点A、B关于x轴对称,求a、b的值;
(2)若A、B关于y轴对称,求﹙4a+b﹚2014的值.
14.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)若△A1B1C1与△ABC关于y轴成轴对称,则△A1B1C1三个顶点坐标分别为A1_____,B1_____,C1_____
(2)在y轴上是否存在点Q.使得S△ACQ=S△ABC,如果存在,求出点Q的坐标,如果不存在,说明理由;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标是_____.
第一课时答案
一、单选题
C.D.A.D.A.
二、填空题
6.-6.
7.8.
8.12cm.
9.70.
三、解答题
10.
解:
(1)如图;
(2)如图;
(3)点B′的坐标为(2,1).
11.
(1)解:如图所示:△A1B1C1就是所要求作的图形、
(2)△A2B2C2就是所要求作的图形;
(3)如果AC上有一点P(m,n)经过上述两次变换,那么对应A2C2上的点P2的坐标是:
故答案为(m 3, n).
12.
解:如图所示,分别以直线OX、OY为对称轴,作点P的对称点与,
连接,分别交OX于点M,交OY于点N,则PM+MN+NP最短.
13.
∵A点和E点关于BD对称,
∴∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD.
又B点、C点关于DE对称,
∴∠DBE=∠C,∠ABC=2∠C.
∵∠A=90°,∴∠ABC+∠C=2∠C+∠C=3∠C=90°.
∴∠C=30°,
∴∠ABC=2∠C=60°.
14.
()证明:∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
∴,
在△ABD和△ACD′中,
∵ ,
∴ △ABD≌△ACD′(SSS).
()解:∵≌,
∴,
∴,
∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
∴,
即.
第二课时答案
一、单选题
C.A.A.B.C
二、填空题
6.116°
7.3.
8.(1,2)、(-1,-2)、(-1,2)
9.(-4,2)或(-4,3)
三、解答题
10.作点A关于燃气管道的对称点A′,连接A′B交燃气管道于点P,即点P即为所求.
11.(1)如图所示:
(2)S=5×4-×4×1-×4×1-×5×3=8.5.
12.(1)△A1B1C1如图所示,A1(-1,1),B1(-4,2),C1(-3,4);
(2)如图1,找出A的对称点A′(1,﹣1),连接BA′,与x轴交点即为P,点P坐标为(2,0);
(3)设存在点 Q,使得S△AOQ=S△ABC,如图2,作AD⊥y轴于D,设Q点坐标为(0,y),则 OQ=|y|,AD=1,
S△ABC==,
由题意,S△AOQ=S△ABC,得 ,
或,
∴ Q点坐标为(0,)或(0,).
13.
解:(1)∵点A,B关于x轴对称,
∴,
解得;
(2)∵A,B关于y轴对称,
∴,
解得,
所以(4a+b)2016=[4×(-1)+3]2016=1.
14.
(1)△A1B1C1如图所示,A1(﹣1,1),B1(﹣4,2),C1(﹣3,4).
故答案为(﹣1,1),(﹣4,2),(﹣3,4).
(2)存在.设Q(0,m),
∵S△ABC=9﹣×2×3﹣×3×1﹣×1×2=,
∴S△QAC=,
∴|m| 3﹣ |m| 1=,
∴m=±,
∴Q(0,)或(0,﹣).
(3)如图作点B关于x轴的对称点B′,连接AB′交x轴于P,此时PA+PB的值最小,此时P(2,0).
