七年级数学上册试题 1.2数轴、相反数和绝对值同步练习-沪科版(含答案)
文档属性
| 名称 | 七年级数学上册试题 1.2数轴、相反数和绝对值同步练习-沪科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 467.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 00:00:00 | ||
图片预览




文档简介
1.2数轴、相反数和绝对值
第一课时
一、单选题
1.实数a,b,c在数轴上的对应点的位置如图所示,那么这三个数中绝对值最大的是( )
A.a B.b C.c D.无法确定
2.一实验室检测A、B、C、D四个元件的质量(单位:克),超过标准质量的克数记为正数,不足标准质量的克数记为负数,结果如图所示,其中最接近标准质量的元件是( )
A. B. C. D.
3.点A在数轴上,点A所对应的数用表示,且点A到原点的距离等于3,则a的值为( )
A.或1 B.或2 C. D.1
4.有理数a,b,c在数轴上的位置如图所示,下列关系正确的是( )
A.|a|>|b| B.a>﹣b C.b<﹣a D.﹣a=b
5.化简=( )
A.—3.14 B.3.14+ C.3.14— D.0
二、填空题
6.若在数轴上对应的点到表示的点的距离为3,则__________.
7.的相反数为__________.
8.正方形ABCD在数轴上的位置如图,点A、D对应的数分别为0和-1.若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1.则连续翻转5次后,数轴上5所对应的点是________;连续翻转2019次后,数轴上数2019所对应的点是________.
9.点A,B在数轴上分别表示有理数a、b.A,B两点之间的距离表示为AB,在数轴上A,B两点之间的距离.
利用数形结合思想回答下列问题:
①数轴上表示1和3两点之间的距离是________;
②x表示一个有理数,且,则有理数x的值是_________.
三、解答题
10.在数轴上表示下列各数:,0,,-4,,并把它们用“<”连接起来.
11.如图,数轴的单位长度为点表示的数互为相反数.
(1)直接写出:点表示的数是_____,点表示的数是_____.
(2)如果数轴上点到点的距离和等于则点表示的数是 .
(3)数轴上动点从点出发以每秒个单位长度的速度向左运动,同时另一动点从点出发以每秒个单位长度的速度也向左运动.运动秒后两点间的距离为求出的值.
12.结合数轴和绝对值的知识回答下列问题:
(1)数轴上,表示1和4的两点之间的距离是_________,表示和2的两点之间的距离是________;
(2)数轴上,表示数和数的两点之间的距离可表示为____________.如果表示数和的两点之间的距离是3,那么_________;
(3)若数轴上表示数的点位于和2之间,求的值;
(4)当取何值时,的值最小?最小值是多少?请说明理由.
13.已知A、B在数轴上分别表示a,b.
(1)对照数轴填写下表:
a 6 -6 -6 -6 2 -1.5
b 4 0 4 -4 -10 -1.5
A、B两点的距离
(2)若A、B两点间的距离记为d,试问:d和a,b有何数量关系
(3)在数轴上找出所有符合条件的整数点P,使它到5和-5的距离之和为10,并求所有这些整数的和;
(4)若点C表示的数为x,当点C在什么位置时,取得的值最小 最小值是多少?
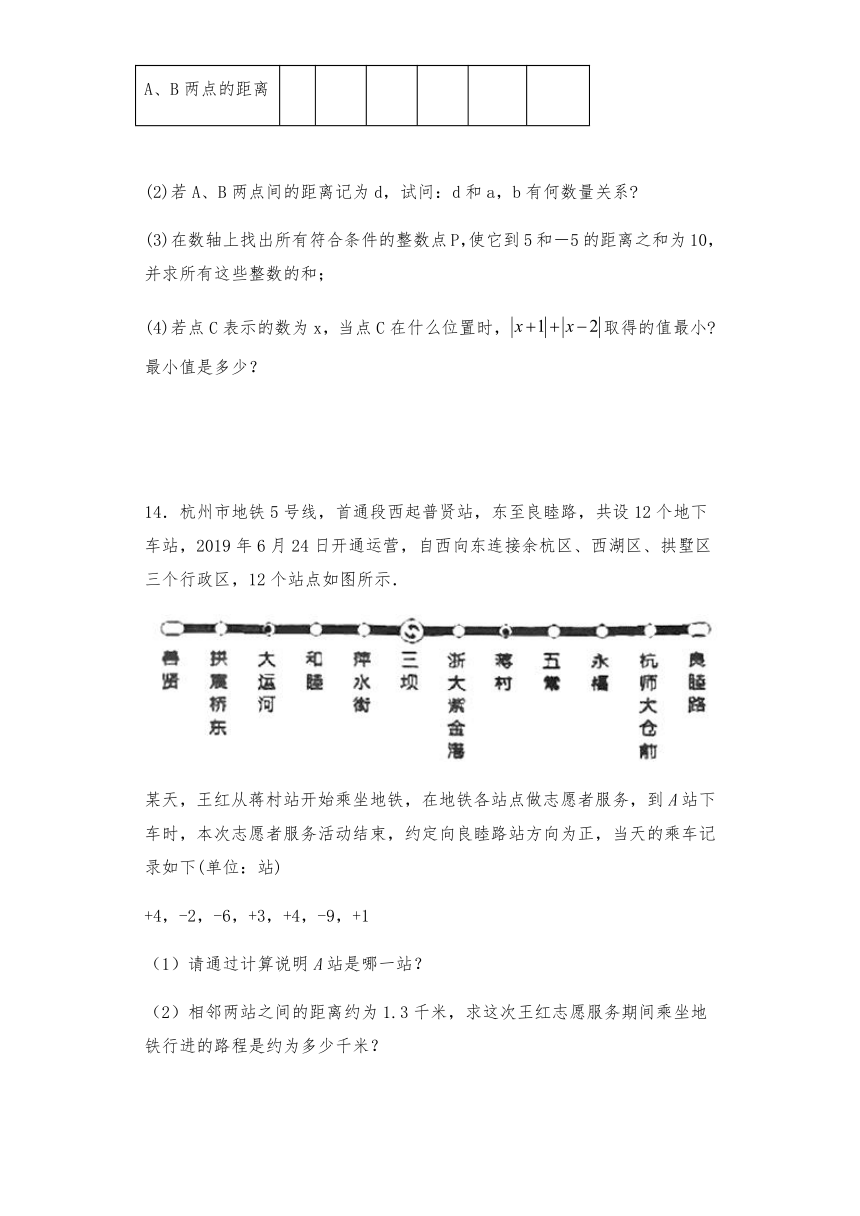
14.杭州市地铁5号线,首通段西起普贤站,东至良睦路,共设12个地下车站,2019年6月24日开通运营,自西向东连接余杭区、西湖区、拱墅区三个行政区,12个站点如图所示.
某天,王红从蒋村站开始乘坐地铁,在地铁各站点做志愿者服务,到A站下车时,本次志愿者服务活动结束,约定向良睦路站方向为正,当天的乘车记录如下(单位:站)
+4,-2,-6,+3,+4,-9,+1
(1)请通过计算说明A站是哪一站?
(2)相邻两站之间的距离约为1.3千米,求这次王红志愿服务期间乘坐地铁行进的路程是约为多少千米?
第二课时
一、单选题
1.如图数轴所示,下列结论正确的是( )
A.a>0 B.b>0 C.b>a D.>
2.数轴上有A,B,C,D四个点,其中绝对值相等的点是( )
A.点A与点D B.点A与点C C.点B与点C D.点B与点D
3.点(为正整数)都在数轴上,点在原点的左边,且;点在点的右边,且;点在点的左边,且;点在点的右边,且;…,依照上述规律,点所表示的数分别为 ( )
A.2018,-2019 B.1009,-1010
C.-2018,2019 D.-1009,1009
4.如图,在纸面所在的平面内,一只电子蚂蚁从数轴上表示原点的位置O点出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其移动路线如图所示,第1次移动到,第2次移动到,第3次移动到,……,第n次移动到,则△O的面积是( )
A.504 B. C. D.505
5.如图,数轴上有三个点A、B、C,若点A、B表示的数互为相反数,则图中点C对应的数是( )
A.﹣2 B.0 C.1 D.4
二、填空题
6.化简下列各式:
+(–7)=_____,–(+1.4)=_____,+(+2.5)=______,–[+(–5)]= ______;–[–(–2.8)]= ________,–(–6)=_____,–[–(+6)]= ______.
7.若、互为相反数,、互为倒数,则__________.
8.在数轴上与所对应的点相距4个单位长度的点表示的数是______.
9.已知在数轴上的对应点如图所示,化简__________.
三、解答题
10.如图,数轴的单位长度为点表示的数互为相反数.
(1)直接写出:点表示的数是_____,点表示的数是_____.
(2)如果数轴上点到点的距离和等于则点表示的数是 .
(3)数轴上动点从点出发以每秒个单位长度的速度向左运动,同时另一动点从点出发以每秒个单位长度的速度也向左运动.运动秒后两点间的距离为求出的值.
11.结合数轴和绝对值的知识回答下列问题:
(1)数轴上,表示1和4的两点之间的距离是_________,表示和2的两点之间的距离是________;
(2)数轴上,表示数和数的两点之间的距离可表示为____________.如果表示数和的两点之间的距离是3,那么_________;
(3)若数轴上表示数的点位于和2之间,求的值;
(4)当取何值时,的值最小?最小值是多少?请说明理由.
12.有一列数:,1,3,﹣3,﹣1,﹣2.5;
(1)画一条数轴,并把上述各数在数轴上表示出来;
(2)把这一列数按从小到大的顺序排列起来,并用“<”连接.
13.小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东跑回到自己家.
(1)以小明家为原点,向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250米/分钟,那么小明跑步一共用了多长时间?
14.有理数a,b,c在数轴上的位置如图所示,且表示数a的点、数b的点与原点的距离相等.
(1)用“>”“<”或“=”填空:b______0,a+b______0,a-c______0,b-c______0;
(2)|b-1|+|a-1|=________;
(3)化简:|a+b|+|a-c|-|b|+|b-c|.
第一课时答案
一、单选题
A.D.A.C.A.
二、填空题
6.﹣5或1
7.2020.
8.B D
9.2 -5或3
三、解答题
10.
解:数轴如图,
-4<0<<<.
11.
解:(1)∵点A,D表示的数互为相反数,
∴数轴的原点位于点B右侧一个单位,
∴点B表示的数是 1,点C表示的数是2,
故答案为: 1;2.
(2)设点P表示的数为x,
∵点B,C的距离为3,
∴若点P到点B,C的距离和等于5,则点P可能位于点B左侧或者位于点C右侧,
∴当点P位于点B左侧时,
|x ( 1)|+|x 2|
= 1 x+2 x
=1 2x
=5
∴x= 2
当点P位于点C右侧时,
|x ( 1)|+|x 2|
=x+1+x 2
=2x 1
=5
∴x=3
故答案为: 2或3.
(3)由题意得:
|(2 2x) ( 1 x)|=1
∴|3 x|=1
∴3 x=1或3 x= 1
∴x=2或x=4
即x的值为2或4.
12.
解:(1)表示和的两点之间的距离是,
表示和的两点之间的距离是;
(2)①表示数和数的两点之间的距离可表示为
②∵数和的两点之间的距离是
∴
∴或;
(3)∵数轴上表示数的点位于和2之间
∴,
∴
;
(4)∵为表示和两点之间的距离,为表示和两点之间的距离,为表示和两点之间的距离,如图:
∴观察数轴可知,根据两点之间线段最短的原理,当时,有最小值,最小值为.
故答案是:(1),(2),或(3)(4)当时,有最小值,最小值为
13.
(1)由题意,得
A、B两点间的距离依次为:2,6,10,2,12,0;
(2)由题意,得
(3)到两定点距离之和等于两定点之间的距离的点的集合是两定点之间的连线
故p点一定在5和-5之间
这样的整数点有1,2,3,4,5,-5,-4,-3,-2,-1,0
故它们的和为0;
(4)由题意,得
表示x到-1的距离,同理表示x到2的距离,
∴点C在-1和2之间时,取得最小值,最小值为3.
14.
解:(1)
∴A站是大运河站;
(2),
29×1.3=37.7(千米)
第二课时答案
一、单选题
A.C. B.B.C.
二、填空题
6.–7, –1.4, 2.5, 5 , –2.8 , 6, 6.
7.2.
8.2或﹣6
9.a
三、解答题
10.解:(1)∵点A,D表示的数互为相反数,
∴数轴的原点位于点B右侧一个单位,
∴点B表示的数是 1,点C表示的数是2,
故答案为: 1;2.
(2)设点P表示的数为x,
∵点B,C的距离为3,
∴若点P到点B,C的距离和等于5,则点P可能位于点B左侧或者位于点C右侧,
∴当点P位于点B左侧时,
|x ( 1)|+|x 2|
= 1 x+2 x
=1 2x
=5
∴x= 2
当点P位于点C右侧时,
|x ( 1)|+|x 2|
=x+1+x 2
=2x 1
=5
∴x=3
故答案为: 2或3.
(3)由题意得:
|(2 2x) ( 1 x)|=1
∴|3 x|=1
∴3 x=1或3 x= 1
∴x=2或x=4
即x的值为2或4.
11.解:(1)表示和的两点之间的距离是,
表示和的两点之间的距离是;
(2)①表示数和数的两点之间的距离可表示为
②∵数和的两点之间的距离是
∴
∴或;
(3)∵数轴上表示数的点位于和2之间
∴,
∴
;
(4)∵为表示和两点之间的距离,为表示和两点之间的距离,为表示和两点之间的距离,如图:
∴观察数轴可知,根据两点之间线段最短的原理,当时,有最小值,最小值为.
故答案是:(1),(2),或(3)(4)当时,有最小值,最小值为
12.(1)把各数表示到数轴上如下图所示:
;
(2)根据数轴上的点表示的数,左边的总小于右边的结合(1)可得:
﹣3<﹣2.5<﹣1<<1<3.
13.(1)如图所示:
(2)小彬家与学校的距离是:2﹣(﹣1)=3(km).
故小彬家与学校之间的距离是 3km;
(3)小明一共跑了(2+1.5+1)×2=9(km), 小明跑步一共用的时间是:9000÷250=36(分钟).
答:小明跑步一共用了 36 分钟长时间.
14.,,
(1),,,,
故答案为:<;=;>;<
(2),
故答案为:a-b
(3)原式=|0|+(a-c)+b-(b-c)=0+a-c+b-b+c=a.
故答案为:.
第一课时
一、单选题
1.实数a,b,c在数轴上的对应点的位置如图所示,那么这三个数中绝对值最大的是( )
A.a B.b C.c D.无法确定
2.一实验室检测A、B、C、D四个元件的质量(单位:克),超过标准质量的克数记为正数,不足标准质量的克数记为负数,结果如图所示,其中最接近标准质量的元件是( )
A. B. C. D.
3.点A在数轴上,点A所对应的数用表示,且点A到原点的距离等于3,则a的值为( )
A.或1 B.或2 C. D.1
4.有理数a,b,c在数轴上的位置如图所示,下列关系正确的是( )
A.|a|>|b| B.a>﹣b C.b<﹣a D.﹣a=b
5.化简=( )
A.—3.14 B.3.14+ C.3.14— D.0
二、填空题
6.若在数轴上对应的点到表示的点的距离为3,则__________.
7.的相反数为__________.
8.正方形ABCD在数轴上的位置如图,点A、D对应的数分别为0和-1.若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1.则连续翻转5次后,数轴上5所对应的点是________;连续翻转2019次后,数轴上数2019所对应的点是________.
9.点A,B在数轴上分别表示有理数a、b.A,B两点之间的距离表示为AB,在数轴上A,B两点之间的距离.
利用数形结合思想回答下列问题:
①数轴上表示1和3两点之间的距离是________;
②x表示一个有理数,且,则有理数x的值是_________.
三、解答题
10.在数轴上表示下列各数:,0,,-4,,并把它们用“<”连接起来.
11.如图,数轴的单位长度为点表示的数互为相反数.
(1)直接写出:点表示的数是_____,点表示的数是_____.
(2)如果数轴上点到点的距离和等于则点表示的数是 .
(3)数轴上动点从点出发以每秒个单位长度的速度向左运动,同时另一动点从点出发以每秒个单位长度的速度也向左运动.运动秒后两点间的距离为求出的值.
12.结合数轴和绝对值的知识回答下列问题:
(1)数轴上,表示1和4的两点之间的距离是_________,表示和2的两点之间的距离是________;
(2)数轴上,表示数和数的两点之间的距离可表示为____________.如果表示数和的两点之间的距离是3,那么_________;
(3)若数轴上表示数的点位于和2之间,求的值;
(4)当取何值时,的值最小?最小值是多少?请说明理由.
13.已知A、B在数轴上分别表示a,b.
(1)对照数轴填写下表:
a 6 -6 -6 -6 2 -1.5
b 4 0 4 -4 -10 -1.5
A、B两点的距离
(2)若A、B两点间的距离记为d,试问:d和a,b有何数量关系
(3)在数轴上找出所有符合条件的整数点P,使它到5和-5的距离之和为10,并求所有这些整数的和;
(4)若点C表示的数为x,当点C在什么位置时,取得的值最小 最小值是多少?
14.杭州市地铁5号线,首通段西起普贤站,东至良睦路,共设12个地下车站,2019年6月24日开通运营,自西向东连接余杭区、西湖区、拱墅区三个行政区,12个站点如图所示.
某天,王红从蒋村站开始乘坐地铁,在地铁各站点做志愿者服务,到A站下车时,本次志愿者服务活动结束,约定向良睦路站方向为正,当天的乘车记录如下(单位:站)
+4,-2,-6,+3,+4,-9,+1
(1)请通过计算说明A站是哪一站?
(2)相邻两站之间的距离约为1.3千米,求这次王红志愿服务期间乘坐地铁行进的路程是约为多少千米?
第二课时
一、单选题
1.如图数轴所示,下列结论正确的是( )
A.a>0 B.b>0 C.b>a D.>
2.数轴上有A,B,C,D四个点,其中绝对值相等的点是( )
A.点A与点D B.点A与点C C.点B与点C D.点B与点D
3.点(为正整数)都在数轴上,点在原点的左边,且;点在点的右边,且;点在点的左边,且;点在点的右边,且;…,依照上述规律,点所表示的数分别为 ( )
A.2018,-2019 B.1009,-1010
C.-2018,2019 D.-1009,1009
4.如图,在纸面所在的平面内,一只电子蚂蚁从数轴上表示原点的位置O点出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其移动路线如图所示,第1次移动到,第2次移动到,第3次移动到,……,第n次移动到,则△O的面积是( )
A.504 B. C. D.505
5.如图,数轴上有三个点A、B、C,若点A、B表示的数互为相反数,则图中点C对应的数是( )
A.﹣2 B.0 C.1 D.4
二、填空题
6.化简下列各式:
+(–7)=_____,–(+1.4)=_____,+(+2.5)=______,–[+(–5)]= ______;–[–(–2.8)]= ________,–(–6)=_____,–[–(+6)]= ______.
7.若、互为相反数,、互为倒数,则__________.
8.在数轴上与所对应的点相距4个单位长度的点表示的数是______.
9.已知在数轴上的对应点如图所示,化简__________.
三、解答题
10.如图,数轴的单位长度为点表示的数互为相反数.
(1)直接写出:点表示的数是_____,点表示的数是_____.
(2)如果数轴上点到点的距离和等于则点表示的数是 .
(3)数轴上动点从点出发以每秒个单位长度的速度向左运动,同时另一动点从点出发以每秒个单位长度的速度也向左运动.运动秒后两点间的距离为求出的值.
11.结合数轴和绝对值的知识回答下列问题:
(1)数轴上,表示1和4的两点之间的距离是_________,表示和2的两点之间的距离是________;
(2)数轴上,表示数和数的两点之间的距离可表示为____________.如果表示数和的两点之间的距离是3,那么_________;
(3)若数轴上表示数的点位于和2之间,求的值;
(4)当取何值时,的值最小?最小值是多少?请说明理由.
12.有一列数:,1,3,﹣3,﹣1,﹣2.5;
(1)画一条数轴,并把上述各数在数轴上表示出来;
(2)把这一列数按从小到大的顺序排列起来,并用“<”连接.
13.小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东跑回到自己家.
(1)以小明家为原点,向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250米/分钟,那么小明跑步一共用了多长时间?
14.有理数a,b,c在数轴上的位置如图所示,且表示数a的点、数b的点与原点的距离相等.
(1)用“>”“<”或“=”填空:b______0,a+b______0,a-c______0,b-c______0;
(2)|b-1|+|a-1|=________;
(3)化简:|a+b|+|a-c|-|b|+|b-c|.
第一课时答案
一、单选题
A.D.A.C.A.
二、填空题
6.﹣5或1
7.2020.
8.B D
9.2 -5或3
三、解答题
10.
解:数轴如图,
-4<0<<<.
11.
解:(1)∵点A,D表示的数互为相反数,
∴数轴的原点位于点B右侧一个单位,
∴点B表示的数是 1,点C表示的数是2,
故答案为: 1;2.
(2)设点P表示的数为x,
∵点B,C的距离为3,
∴若点P到点B,C的距离和等于5,则点P可能位于点B左侧或者位于点C右侧,
∴当点P位于点B左侧时,
|x ( 1)|+|x 2|
= 1 x+2 x
=1 2x
=5
∴x= 2
当点P位于点C右侧时,
|x ( 1)|+|x 2|
=x+1+x 2
=2x 1
=5
∴x=3
故答案为: 2或3.
(3)由题意得:
|(2 2x) ( 1 x)|=1
∴|3 x|=1
∴3 x=1或3 x= 1
∴x=2或x=4
即x的值为2或4.
12.
解:(1)表示和的两点之间的距离是,
表示和的两点之间的距离是;
(2)①表示数和数的两点之间的距离可表示为
②∵数和的两点之间的距离是
∴
∴或;
(3)∵数轴上表示数的点位于和2之间
∴,
∴
;
(4)∵为表示和两点之间的距离,为表示和两点之间的距离,为表示和两点之间的距离,如图:
∴观察数轴可知,根据两点之间线段最短的原理,当时,有最小值,最小值为.
故答案是:(1),(2),或(3)(4)当时,有最小值,最小值为
13.
(1)由题意,得
A、B两点间的距离依次为:2,6,10,2,12,0;
(2)由题意,得
(3)到两定点距离之和等于两定点之间的距离的点的集合是两定点之间的连线
故p点一定在5和-5之间
这样的整数点有1,2,3,4,5,-5,-4,-3,-2,-1,0
故它们的和为0;
(4)由题意,得
表示x到-1的距离,同理表示x到2的距离,
∴点C在-1和2之间时,取得最小值,最小值为3.
14.
解:(1)
∴A站是大运河站;
(2),
29×1.3=37.7(千米)
第二课时答案
一、单选题
A.C. B.B.C.
二、填空题
6.–7, –1.4, 2.5, 5 , –2.8 , 6, 6.
7.2.
8.2或﹣6
9.a
三、解答题
10.解:(1)∵点A,D表示的数互为相反数,
∴数轴的原点位于点B右侧一个单位,
∴点B表示的数是 1,点C表示的数是2,
故答案为: 1;2.
(2)设点P表示的数为x,
∵点B,C的距离为3,
∴若点P到点B,C的距离和等于5,则点P可能位于点B左侧或者位于点C右侧,
∴当点P位于点B左侧时,
|x ( 1)|+|x 2|
= 1 x+2 x
=1 2x
=5
∴x= 2
当点P位于点C右侧时,
|x ( 1)|+|x 2|
=x+1+x 2
=2x 1
=5
∴x=3
故答案为: 2或3.
(3)由题意得:
|(2 2x) ( 1 x)|=1
∴|3 x|=1
∴3 x=1或3 x= 1
∴x=2或x=4
即x的值为2或4.
11.解:(1)表示和的两点之间的距离是,
表示和的两点之间的距离是;
(2)①表示数和数的两点之间的距离可表示为
②∵数和的两点之间的距离是
∴
∴或;
(3)∵数轴上表示数的点位于和2之间
∴,
∴
;
(4)∵为表示和两点之间的距离,为表示和两点之间的距离,为表示和两点之间的距离,如图:
∴观察数轴可知,根据两点之间线段最短的原理,当时,有最小值,最小值为.
故答案是:(1),(2),或(3)(4)当时,有最小值,最小值为
12.(1)把各数表示到数轴上如下图所示:
;
(2)根据数轴上的点表示的数,左边的总小于右边的结合(1)可得:
﹣3<﹣2.5<﹣1<<1<3.
13.(1)如图所示:
(2)小彬家与学校的距离是:2﹣(﹣1)=3(km).
故小彬家与学校之间的距离是 3km;
(3)小明一共跑了(2+1.5+1)×2=9(km), 小明跑步一共用的时间是:9000÷250=36(分钟).
答:小明跑步一共用了 36 分钟长时间.
14.,,
(1),,,,
故答案为:<;=;>;<
(2),
故答案为:a-b
(3)原式=|0|+(a-c)+b-(b-c)=0+a-c+b-b+c=a.
故答案为:.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
