2023—2024学年人教版数学七年级上册1.2.2数轴 课件(共23张PPT)
文档属性
| 名称 | 2023—2024学年人教版数学七年级上册1.2.2数轴 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 810.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
1.2 有理数
1.2.2 数轴
学习目标:
1、了解数轴的概念,掌握数轴的画法并会用数轴上的点表示有理数;
2、理解有理数和数轴上的点的对应关系.
学习重难点:
重点:数轴的画法及用数轴上的点表示有理数;
难点:理解有理数和数轴上的点的对应关系.
问题思考
在一条东西向的马路上,有一个汽车站牌,汽车站牌东3 m和7.5 m处有一棵柳树和一棵杨树,汽车站牌西3 m和4.8 m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
0
3
7.5
3
4.8
思考:怎样用数简明地表示这些树、电线杆与汽车站牌的相对
位置关系(方向、距离)?
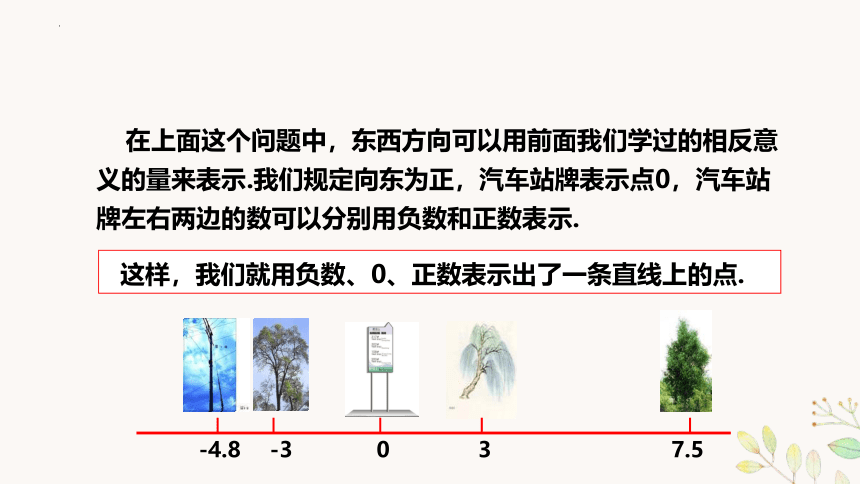
在上面这个问题中,东西方向可以用前面我们学过的相反意义的量来表示.我们规定向东为正,汽车站牌表示点0,汽车站牌左右两边的数可以分别用负数和正数表示.
这样,我们就用负数、0、正数表示出了一条直线上的点.
0
3
7.5
-3
-4.8
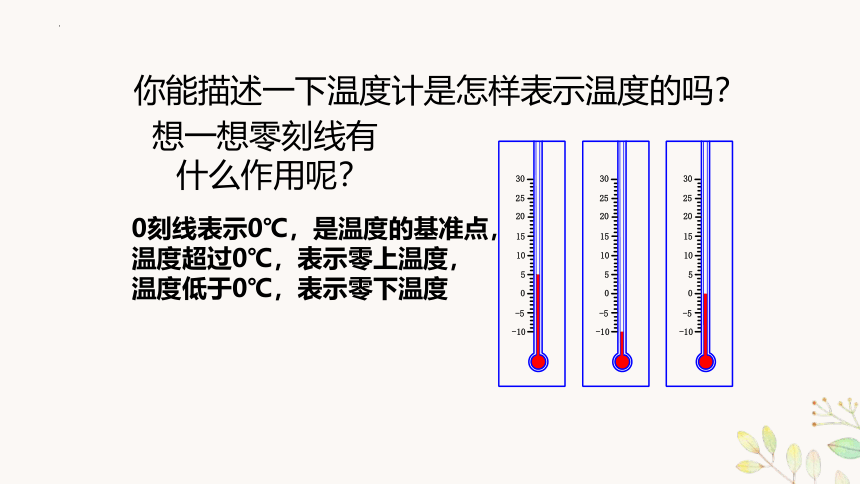
你能描述一下温度计是怎样表示温度的吗?
想一想零刻线有什么作用呢?
0刻线表示0℃,是温度的基准点,
温度超过0℃,表示零上温度,
温度低于0℃,表示零下温度
怎样读出某一时刻温度计上显示的温度?
首先要观察引时温度计中红色液面在0刻线的上面、下面还是与它重合;
其次要确定此时红色液面对应的刻度;
最后要求得这个刻度与0刻线之间的距离。
读一读:请同学们分别读出右边两图中的温度计显示的某个时刻的温度
观察
1、提问,到底什么是数轴?如何画数轴?
0
1
2
3
-1
-2
-3
原点
正方向(向右或向上)
单位长度
导学施教
步骤:
1、画一条直线,在直线上任取一个点表示数0,这个点叫做原点;
原点的作用:原点是数轴的“基准点”
2、通常规定,直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
3、选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,…;从原点向左,用类似方法依次表-1,-2,-3,…
注意:同一数轴上单位长度表示的量是相同的
规定了原点、正方向和单位长度的直线叫做数轴。
一、 得出定义,揭示内涵
同桌之间互相说一说什么叫做数轴?
数轴的概念
A,B,C,D四名同学画出的数轴如图所示,其中正确的是( )
解析:
数轴必须具有三要素:原点、正方向和单位长度,缺一不可,本题考查学生对图形的判断能力.
点评:
D
0
1
数轴的画法
2
3
-1
-2
-3
(1)取原点
(2)规定正方向,通常取向右为正方向
(3)选取适当的长度为单位长度
规定了原点、正方向和单位长度的直线叫做数轴。
观察下列图形,指出哪条数轴画得正确,其余错在哪里?
1
2
3
A
0
1
-1
2
B
1
0
1
-1
-2
2
E
-1
0
D
-2
-2
0
2
-4
-6
4
C
6
说一说
分数或小数能用数轴上的点来表示吗
怎么表示3.5呢?
怎么表示 呢?
从原点向右3.5个单位长度.
从原点向左 个单位长度.
可以
所有有理数都能用数轴上的点表示出来.
用数轴上的点表示小数和分数
3.5
观察数轴上的点的特点:
数轴上表示数3的点在原点的___边,
与原点的距离是___个单位长度;
表示数-2的点在原点的____边 ,
与原点的距离是___个单位长度.
一般地,设a是一个正数,
则数轴上表示数a的点在原点的______边,
与原点的距离是______个单位长度;
表示数-a的点在原点的______边,
与原点的距离是______个单位长度.
右
3
左
2
右
a
左
a
观察与归纳
例1 在所给数轴上画出表示下列各数的点.
1,-5,-2.5, 0 ,
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5 -4 -3 -2 -1 0 1 2 3 4 5
解:
1
-5
4
●
●
●
●
●
-2.5
0
注意:
①把点标在线上;
②把数标在点的上方, 以便观看.
4
典例精析
一般地,设a是一个正数,则数轴上表示数a的点在原点的____边,与原点的距离是____个单位长度;表示数-a的点在原点的____边,与原点的距离是____个单位长度.
右
a
左
a
归纳
随堂演练
1.在数轴上点A表示的数是-3,与点A相距两个单位的点表示的数是__________.
-1或-5
基础巩固
2.写出数轴上点A,B,C,D,E所表示的数: 3、在数轴上表示下列有理数:1.5,-2,2,-2.5, ,
0
2
-2
1.5
-2.5
4.在数轴上P点表示2,现在将P点向右移动两个单位长度后再向左移动5个单位长度,这时P点表示的数是_______.
综合应用
-1
通过本节课的学习,我们需掌握:
1.数轴的概念:规定了原点、正方向、单位长度的直线.
2.数轴的画法:一画二定三方向四单位.
3.用数轴上的点表示数.
再 见
1.2 有理数
1.2.2 数轴
学习目标:
1、了解数轴的概念,掌握数轴的画法并会用数轴上的点表示有理数;
2、理解有理数和数轴上的点的对应关系.
学习重难点:
重点:数轴的画法及用数轴上的点表示有理数;
难点:理解有理数和数轴上的点的对应关系.
问题思考
在一条东西向的马路上,有一个汽车站牌,汽车站牌东3 m和7.5 m处有一棵柳树和一棵杨树,汽车站牌西3 m和4.8 m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
0
3
7.5
3
4.8
思考:怎样用数简明地表示这些树、电线杆与汽车站牌的相对
位置关系(方向、距离)?
在上面这个问题中,东西方向可以用前面我们学过的相反意义的量来表示.我们规定向东为正,汽车站牌表示点0,汽车站牌左右两边的数可以分别用负数和正数表示.
这样,我们就用负数、0、正数表示出了一条直线上的点.
0
3
7.5
-3
-4.8
你能描述一下温度计是怎样表示温度的吗?
想一想零刻线有什么作用呢?
0刻线表示0℃,是温度的基准点,
温度超过0℃,表示零上温度,
温度低于0℃,表示零下温度
怎样读出某一时刻温度计上显示的温度?
首先要观察引时温度计中红色液面在0刻线的上面、下面还是与它重合;
其次要确定此时红色液面对应的刻度;
最后要求得这个刻度与0刻线之间的距离。
读一读:请同学们分别读出右边两图中的温度计显示的某个时刻的温度
观察
1、提问,到底什么是数轴?如何画数轴?
0
1
2
3
-1
-2
-3
原点
正方向(向右或向上)
单位长度
导学施教
步骤:
1、画一条直线,在直线上任取一个点表示数0,这个点叫做原点;
原点的作用:原点是数轴的“基准点”
2、通常规定,直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
3、选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,…;从原点向左,用类似方法依次表-1,-2,-3,…
注意:同一数轴上单位长度表示的量是相同的
规定了原点、正方向和单位长度的直线叫做数轴。
一、 得出定义,揭示内涵
同桌之间互相说一说什么叫做数轴?
数轴的概念
A,B,C,D四名同学画出的数轴如图所示,其中正确的是( )
解析:
数轴必须具有三要素:原点、正方向和单位长度,缺一不可,本题考查学生对图形的判断能力.
点评:
D
0
1
数轴的画法
2
3
-1
-2
-3
(1)取原点
(2)规定正方向,通常取向右为正方向
(3)选取适当的长度为单位长度
规定了原点、正方向和单位长度的直线叫做数轴。
观察下列图形,指出哪条数轴画得正确,其余错在哪里?
1
2
3
A
0
1
-1
2
B
1
0
1
-1
-2
2
E
-1
0
D
-2
-2
0
2
-4
-6
4
C
6
说一说
分数或小数能用数轴上的点来表示吗
怎么表示3.5呢?
怎么表示 呢?
从原点向右3.5个单位长度.
从原点向左 个单位长度.
可以
所有有理数都能用数轴上的点表示出来.
用数轴上的点表示小数和分数
3.5
观察数轴上的点的特点:
数轴上表示数3的点在原点的___边,
与原点的距离是___个单位长度;
表示数-2的点在原点的____边 ,
与原点的距离是___个单位长度.
一般地,设a是一个正数,
则数轴上表示数a的点在原点的______边,
与原点的距离是______个单位长度;
表示数-a的点在原点的______边,
与原点的距离是______个单位长度.
右
3
左
2
右
a
左
a
观察与归纳
例1 在所给数轴上画出表示下列各数的点.
1,-5,-2.5, 0 ,
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5 -4 -3 -2 -1 0 1 2 3 4 5
解:
1
-5
4
●
●
●
●
●
-2.5
0
注意:
①把点标在线上;
②把数标在点的上方, 以便观看.
4
典例精析
一般地,设a是一个正数,则数轴上表示数a的点在原点的____边,与原点的距离是____个单位长度;表示数-a的点在原点的____边,与原点的距离是____个单位长度.
右
a
左
a
归纳
随堂演练
1.在数轴上点A表示的数是-3,与点A相距两个单位的点表示的数是__________.
-1或-5
基础巩固
2.写出数轴上点A,B,C,D,E所表示的数: 3、在数轴上表示下列有理数:1.5,-2,2,-2.5, ,
0
2
-2
1.5
-2.5
4.在数轴上P点表示2,现在将P点向右移动两个单位长度后再向左移动5个单位长度,这时P点表示的数是_______.
综合应用
-1
通过本节课的学习,我们需掌握:
1.数轴的概念:规定了原点、正方向、单位长度的直线.
2.数轴的画法:一画二定三方向四单位.
3.用数轴上的点表示数.
再 见
