2.4 线段、角的轴对称性同步练习 苏科版八年级数学上册(含答案)
文档属性
| 名称 | 2.4 线段、角的轴对称性同步练习 苏科版八年级数学上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 795.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 21:16:23 | ||
图片预览


文档简介
2.4 线段、角的轴对称性同步练习
一、单选题
1.到三角形三个顶点的距离相等的点是三角形( )的交点.
A.三边垂直平分线 B.三个内角角平分线 C.三条中线D.三条高
2.三条公路将三个A,,村庄连成一个三角形区域,如果在这个区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,那么这个集贸市场应建的位置是( )
A.三条高线的交点 B.三条中线的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
3.一平面镜以与水平面成45°角固定在水平面上,如图所示,一个小球以的速度沿桌面向点O匀速滚去,则小球在平面镜中的像是( )
A.以的速度,做竖直向上运动 B.以的速度,做竖直向下运动
C.以的速度运动,水平向左运动 D.以的速度,水平向左运动
4.在中,,,,分别以点、为圆心、大于线段长度的一半为半径作弧,相交于、,过点、作直线,与相交于点,连接,则的周长为( )
A. B. C. D.
5.如图,在中,已知,,的周长为,分别以A、B两点为圆心,大于的长为半径画弧,两弧相交于点M,N,连接与相交于点D,则的周长为( )
A. B. C. D.
6.如图,在中,,若,,平分,则点到的距离等于( )
A.4 B.3 C.2 D.1
7.如图,,C为OB上的定点,M,N分别为射线OA、OB上的动点.当的值最小时,的度数为( )
A. B. C. D.
8.如图,点是的中点,,,平分且,下列结论:;;;.结论中成立的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题
9.如图,在中,是边上的高,平分,交于点,已知,,,则的面积等于 .
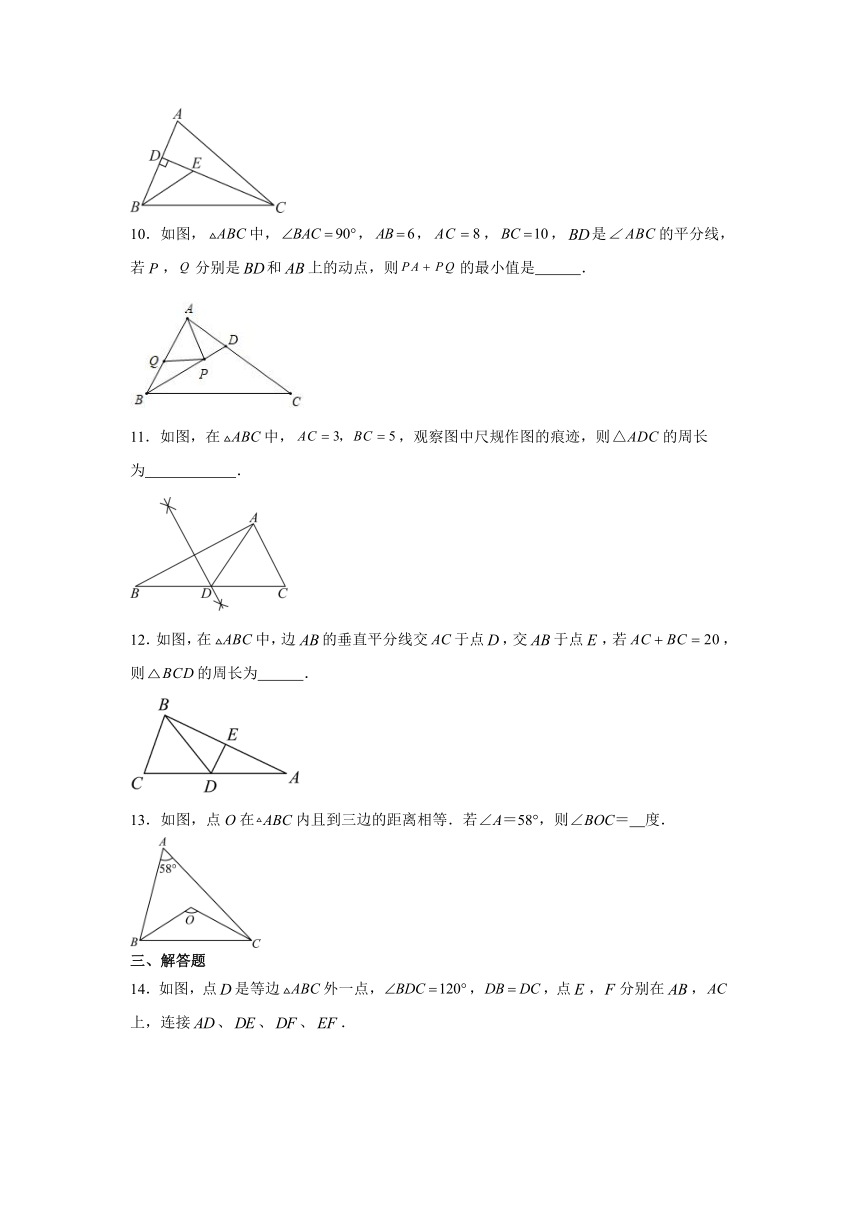
10.如图,中,,,,,是的平分线,若,分别是和上的动点,则的最小值是 .
11.如图,在中,,观察图中尺规作图的痕迹,则的周长为 .
12.如图,在中,边的垂直平分线交于点,交于点,若,则的周长为 .
13.如图,点O在ABC内且到三边的距离相等.若∠A=58°,则∠BOC= 度.
三、解答题
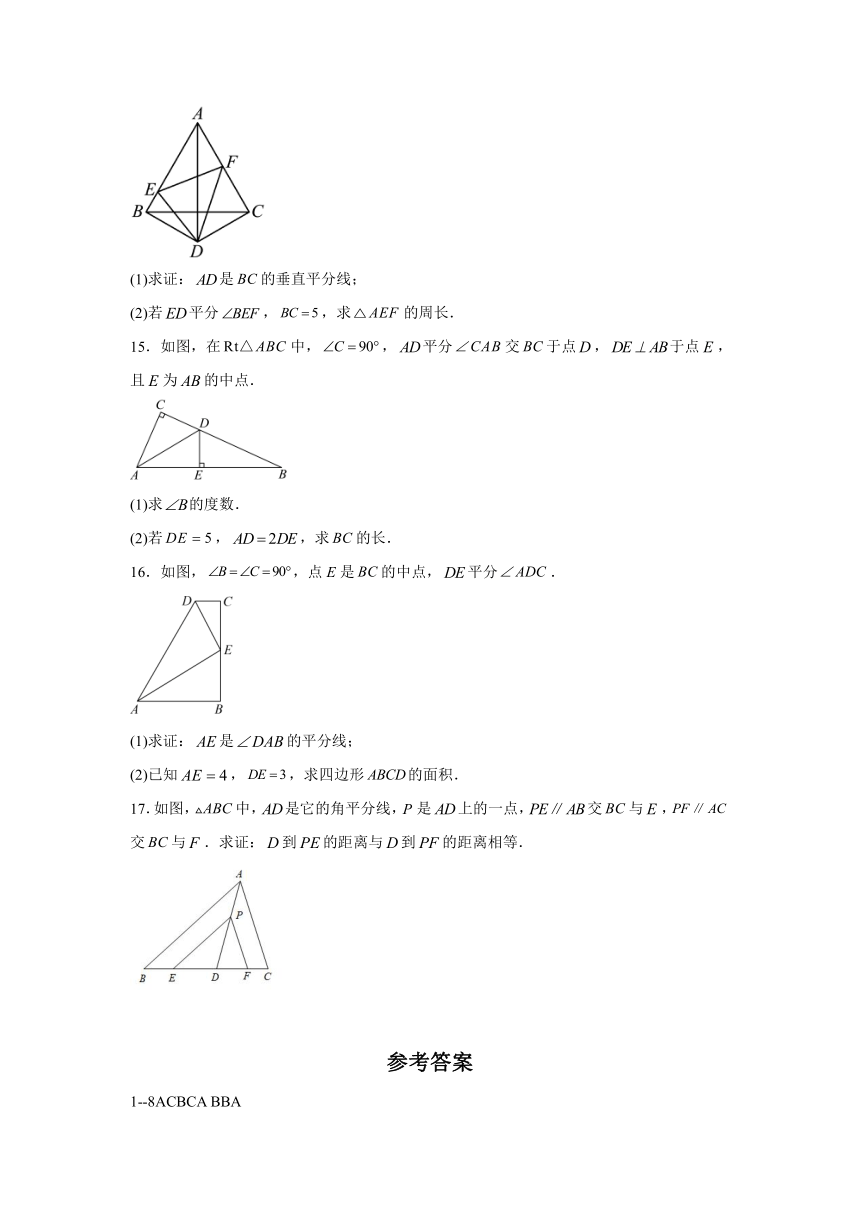
14.如图,点是等边外一点,,,点,分别在,上,连接、、、.
(1)求证:是的垂直平分线;
(2)若平分,,求的周长.
15.如图,在中,,平分交于点,于点,且为的中点.
(1)求的度数.
(2)若,,求的长.
16.如图,,点E是的中点,平分.
(1)求证:是的平分线;
(2)已知,,求四边形的面积.
17.如图,中,是它的角平分线,是上的一点,交与,交与.求证:到的距离与到的距离相等.
参考答案
1--8ACBCA BBA
9.
10.
11.
12.
13.119
14.(1)证明:是等边三角形,
,
∴A在的垂直平分线上,
又,
∴D在的垂直平分线上,
是的垂直平分线;
(2)如图,过D作于M,
,
又是等边三角形,
同理可得
平分,
平分,
在与中
同理可得
.
15.(1)解:平分,
,
∵于点,为的中点,
是线段的垂直平分线,
,,
,;
(2)解:,,
∴,
平分,,,
,
.
16.(1)证明:如图,过点作于点,
∵,平分,
∴,
∵是的中点,
∴,
∴,
又∵,,
∴平分.
(2)解:∵,,
∴和都为,
又∵平分,
∴,
在和中,
,
∴,
∴,,
∵,,
∴和都为,
又∵平分,
∴,
在和中,
,
∴,
∴,,
∴,
∵,,
∴,
∴
.
∴四边形的面积为.
17.证明:过点D作,
∵是的角平分线,
∴,
∵,,
∴,
∴,即是的角平分线,
∵,
∴,即到的距离与到的距离相等.
一、单选题
1.到三角形三个顶点的距离相等的点是三角形( )的交点.
A.三边垂直平分线 B.三个内角角平分线 C.三条中线D.三条高
2.三条公路将三个A,,村庄连成一个三角形区域,如果在这个区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,那么这个集贸市场应建的位置是( )
A.三条高线的交点 B.三条中线的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
3.一平面镜以与水平面成45°角固定在水平面上,如图所示,一个小球以的速度沿桌面向点O匀速滚去,则小球在平面镜中的像是( )
A.以的速度,做竖直向上运动 B.以的速度,做竖直向下运动
C.以的速度运动,水平向左运动 D.以的速度,水平向左运动
4.在中,,,,分别以点、为圆心、大于线段长度的一半为半径作弧,相交于、,过点、作直线,与相交于点,连接,则的周长为( )
A. B. C. D.
5.如图,在中,已知,,的周长为,分别以A、B两点为圆心,大于的长为半径画弧,两弧相交于点M,N,连接与相交于点D,则的周长为( )
A. B. C. D.
6.如图,在中,,若,,平分,则点到的距离等于( )
A.4 B.3 C.2 D.1
7.如图,,C为OB上的定点,M,N分别为射线OA、OB上的动点.当的值最小时,的度数为( )
A. B. C. D.
8.如图,点是的中点,,,平分且,下列结论:;;;.结论中成立的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题
9.如图,在中,是边上的高,平分,交于点,已知,,,则的面积等于 .
10.如图,中,,,,,是的平分线,若,分别是和上的动点,则的最小值是 .
11.如图,在中,,观察图中尺规作图的痕迹,则的周长为 .
12.如图,在中,边的垂直平分线交于点,交于点,若,则的周长为 .
13.如图,点O在ABC内且到三边的距离相等.若∠A=58°,则∠BOC= 度.
三、解答题
14.如图,点是等边外一点,,,点,分别在,上,连接、、、.
(1)求证:是的垂直平分线;
(2)若平分,,求的周长.
15.如图,在中,,平分交于点,于点,且为的中点.
(1)求的度数.
(2)若,,求的长.
16.如图,,点E是的中点,平分.
(1)求证:是的平分线;
(2)已知,,求四边形的面积.
17.如图,中,是它的角平分线,是上的一点,交与,交与.求证:到的距离与到的距离相等.
参考答案
1--8ACBCA BBA
9.
10.
11.
12.
13.119
14.(1)证明:是等边三角形,
,
∴A在的垂直平分线上,
又,
∴D在的垂直平分线上,
是的垂直平分线;
(2)如图,过D作于M,
,
又是等边三角形,
同理可得
平分,
平分,
在与中
同理可得
.
15.(1)解:平分,
,
∵于点,为的中点,
是线段的垂直平分线,
,,
,;
(2)解:,,
∴,
平分,,,
,
.
16.(1)证明:如图,过点作于点,
∵,平分,
∴,
∵是的中点,
∴,
∴,
又∵,,
∴平分.
(2)解:∵,,
∴和都为,
又∵平分,
∴,
在和中,
,
∴,
∴,,
∵,,
∴和都为,
又∵平分,
∴,
在和中,
,
∴,
∴,,
∴,
∵,,
∴,
∴
.
∴四边形的面积为.
17.证明:过点D作,
∵是的角平分线,
∴,
∵,,
∴,
∴,即是的角平分线,
∵,
∴,即到的距离与到的距离相等.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
