第1章反比例函数——一次函数与反比例函数综合题训练 (三)(无答案)2023-2024学年湘教版数学九年级上册
文档属性
| 名称 | 第1章反比例函数——一次函数与反比例函数综合题训练 (三)(无答案)2023-2024学年湘教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 209.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 22:18:58 | ||
图片预览


文档简介
湘教版数学九年级上册第1章反比例函数
一次函数与反比例函数综合题训练三
1. 如图,在平面直角坐标系中,直线与双曲线相交于点,,四边形为菱形,点在轴正半轴上,点的坐标为.
求反比例函数与正比例函数的表达式
过点作轴于点,连接,求的面积
取何值时,请直接写出结果.
2. 如图是反比例函数与反比例函数在第一象限中的图象,点是的图象上一动点,轴于点,交的图象于点,轴于点,交的图象于点,点的横坐标为.
用字母表示点的坐标
求四边形的面积
连接并延长交轴于点,连接,,求证:四边形是平行四边形.
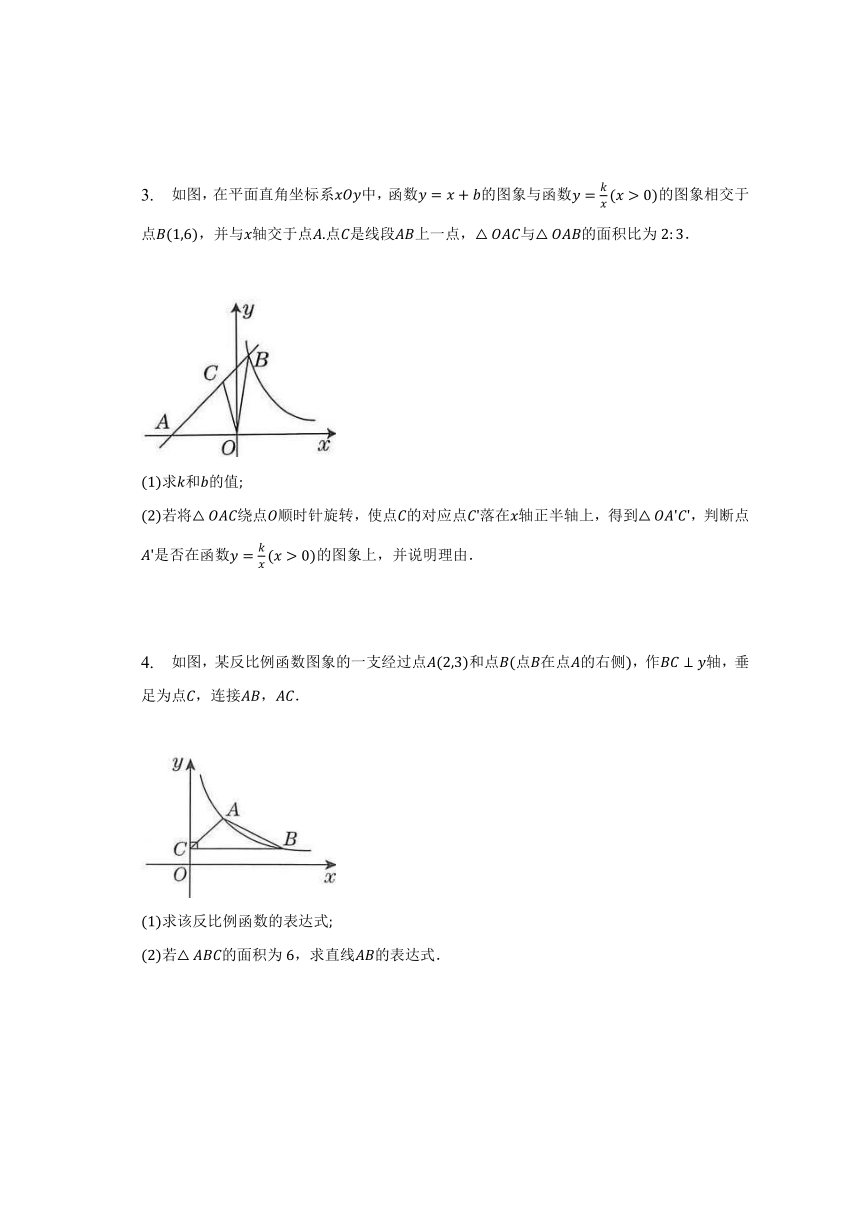
3. 如图,在平面直角坐标系中,函数的图象与函数的图象相交于点,并与轴交于点点是线段上一点,与的面积比为.
求和的值
若将绕点顺时针旋转,使点的对应点落在轴正半轴上,得到,判断点是否在函数的图象上,并说明理由.
4. 如图,某反比例函数图象的一支经过点和点点在点的右侧,作轴,垂足为点,连接,.
求该反比例函数的表达式
若的面积为,求直线的表达式.
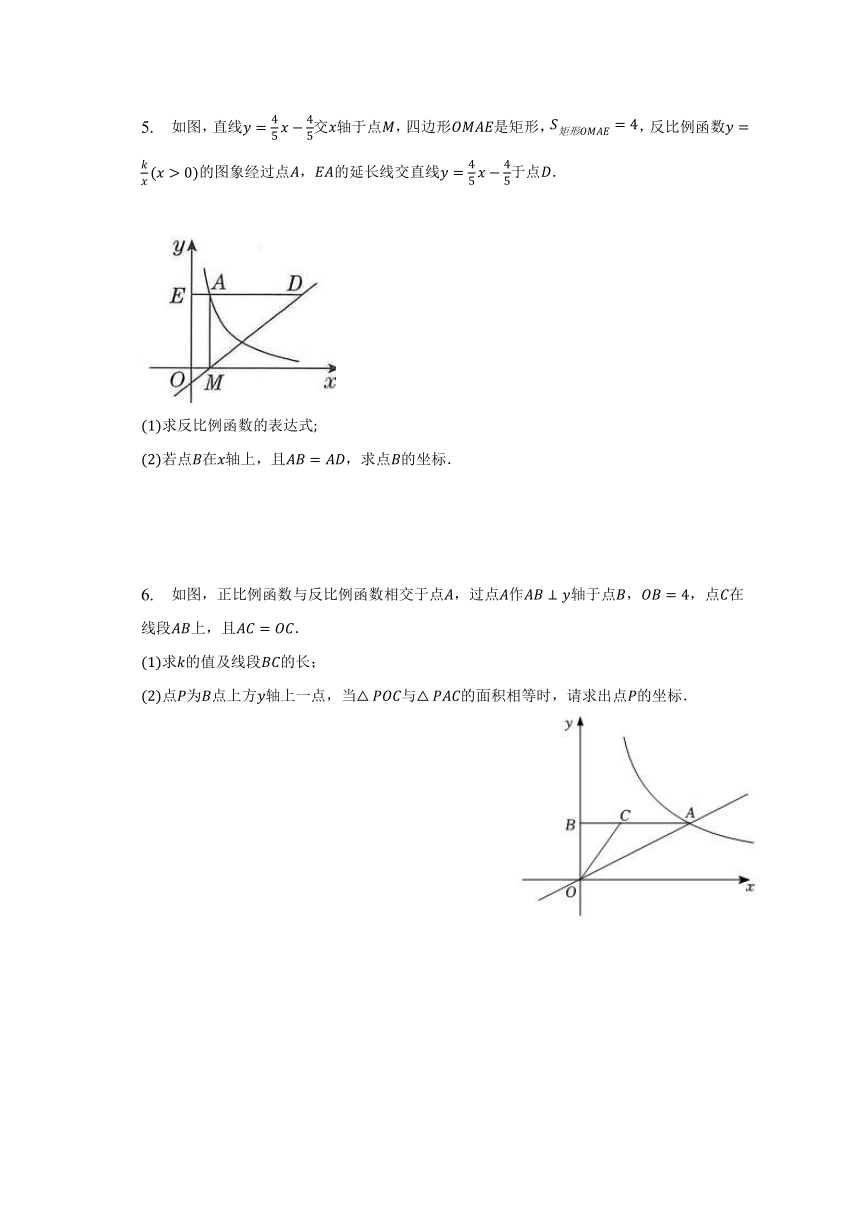
5. 如图,直线交轴于点,四边形是矩形,,反比例函数的图象经过点,的延长线交直线于点.
求反比例函数的表达式
若点在轴上,且,求点的坐标.
6. 如图,正比例函数与反比例函数相交于点,过点作轴于点,,点在线段上,且.
求的值及线段的长;
点为点上方轴上一点,当与的面积相等时,请求出点的坐标.
7. 如图,直线与反比例函数的图象相交于点,,已知点的纵坐标为.
求的值
若点是轴上一点,且的面积为,求点的坐标.
8. 如图,在平面直角坐标系中,直线与反比例函数在第二象限内的图象相交于点.
求反比例函数的解析式;
将直线向上平移后与反比例函数图象在第二象限内交于点,与轴交于点,且的面积为,求直线的解析式.
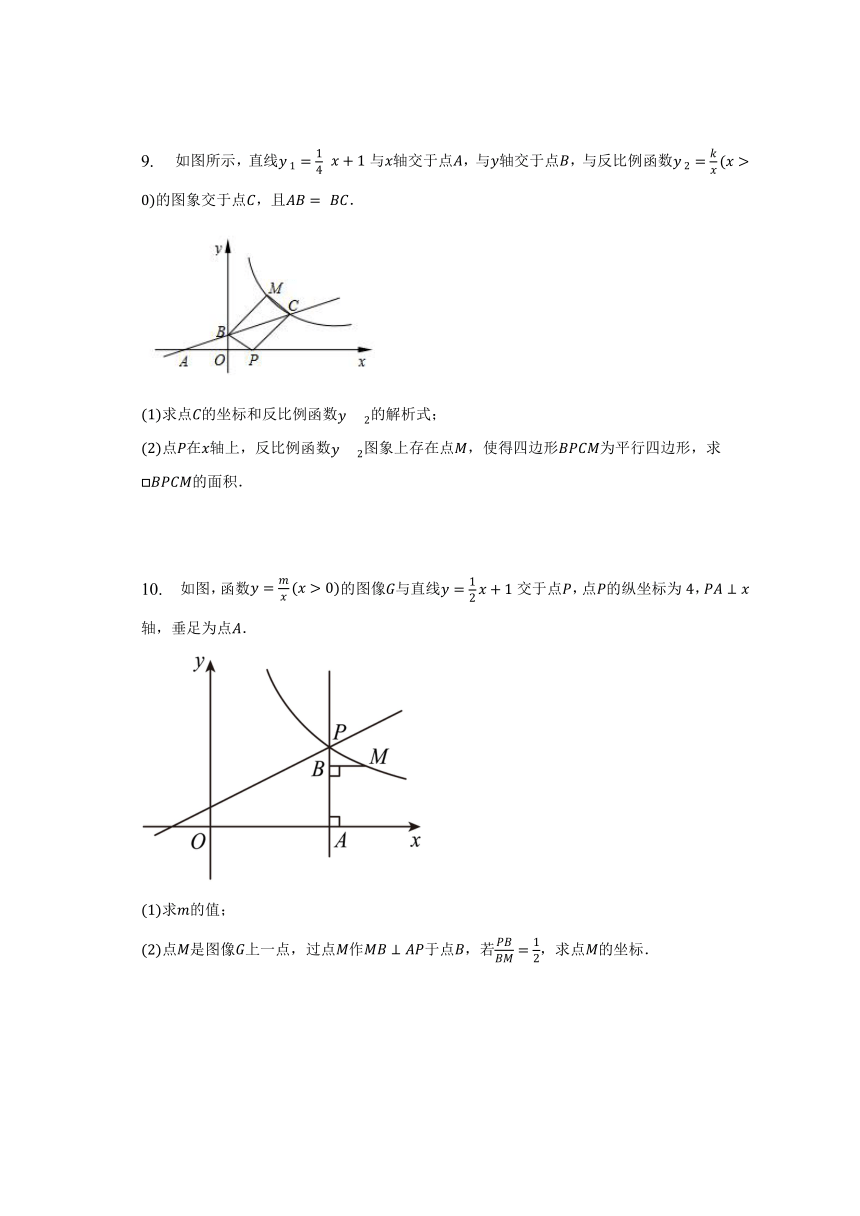
9. 如图所示,直线 与轴交于点,与轴交于点,与反比例函数的图象交于点,且 .
求点的坐标和反比例函数的解析式;
点在轴上,反比例函数图象上存在点,使得四边形为平行四边形,求的面积.
10. 如图,函数的图像与直线交于点,点的纵坐标为,轴,垂足为点.
求的值;
点是图像上一点,过点作于点,若,求点的坐标.
11. 如图,一次函数的图象与反比例函数的图象交于点,.
求反比例函数与一次函数的函数表达式;
请结合图象直接写出不等式的解集;
若点为轴上一点,的面积为,求点的坐标.
12. 如图,在平面直角坐标系中,一次函数的图像与轴交于点,与反比例函数交于点.
求反比例函数的表达式;
点为反比例函数图像上一点,连接,若,求点的坐标.
13. 如图,在平面直角坐标系中,一次函数的图象与轴交于点,与反比例函数的图象交于,两点,点在第一象限,纵坐标为,点在第三象限,轴,垂足为点,.
求反比例函数和一次函数的解析式.
连接,,求四边形的面积.
14. 如图,一次函数与反比例函数的图象交于,两点,与轴相交于点.
求一次函数的表达式
求的面积
在直线上是否存在点,使得,若存在,求出点的坐标,若不存在,请说明理由.
15. 如图,一次函数、为常数,的图象与反比例函数为常数,的图象在第二象限交于点,与轴负半轴交于点,且.
求反比例函数和一次函数的表达式.
根据图象直接写出当时,不等式的解集.
16. 如图,直线与双曲线交于、两点,点的坐标为,经过点直线与轴交于点.
求反比例函数的表达式以及点的坐标;
点是轴上一动点,连接,若是的面积的一半,求此时点的坐标.
17. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于,两点.
求一次函数和反比例函数的解析式;
若点在轴上,位于原点右侧,且,求的面积.
18. 如图,直线与反比例函数的图象相交于点、,过点作轴,垂足为点,连接.
求反比例函数的解析式;
求;
利用函数图象直接写出关于的不等式的解集.
一次函数与反比例函数综合题训练三
1. 如图,在平面直角坐标系中,直线与双曲线相交于点,,四边形为菱形,点在轴正半轴上,点的坐标为.
求反比例函数与正比例函数的表达式
过点作轴于点,连接,求的面积
取何值时,请直接写出结果.
2. 如图是反比例函数与反比例函数在第一象限中的图象,点是的图象上一动点,轴于点,交的图象于点,轴于点,交的图象于点,点的横坐标为.
用字母表示点的坐标
求四边形的面积
连接并延长交轴于点,连接,,求证:四边形是平行四边形.
3. 如图,在平面直角坐标系中,函数的图象与函数的图象相交于点,并与轴交于点点是线段上一点,与的面积比为.
求和的值
若将绕点顺时针旋转,使点的对应点落在轴正半轴上,得到,判断点是否在函数的图象上,并说明理由.
4. 如图,某反比例函数图象的一支经过点和点点在点的右侧,作轴,垂足为点,连接,.
求该反比例函数的表达式
若的面积为,求直线的表达式.
5. 如图,直线交轴于点,四边形是矩形,,反比例函数的图象经过点,的延长线交直线于点.
求反比例函数的表达式
若点在轴上,且,求点的坐标.
6. 如图,正比例函数与反比例函数相交于点,过点作轴于点,,点在线段上,且.
求的值及线段的长;
点为点上方轴上一点,当与的面积相等时,请求出点的坐标.
7. 如图,直线与反比例函数的图象相交于点,,已知点的纵坐标为.
求的值
若点是轴上一点,且的面积为,求点的坐标.
8. 如图,在平面直角坐标系中,直线与反比例函数在第二象限内的图象相交于点.
求反比例函数的解析式;
将直线向上平移后与反比例函数图象在第二象限内交于点,与轴交于点,且的面积为,求直线的解析式.
9. 如图所示,直线 与轴交于点,与轴交于点,与反比例函数的图象交于点,且 .
求点的坐标和反比例函数的解析式;
点在轴上,反比例函数图象上存在点,使得四边形为平行四边形,求的面积.
10. 如图,函数的图像与直线交于点,点的纵坐标为,轴,垂足为点.
求的值;
点是图像上一点,过点作于点,若,求点的坐标.
11. 如图,一次函数的图象与反比例函数的图象交于点,.
求反比例函数与一次函数的函数表达式;
请结合图象直接写出不等式的解集;
若点为轴上一点,的面积为,求点的坐标.
12. 如图,在平面直角坐标系中,一次函数的图像与轴交于点,与反比例函数交于点.
求反比例函数的表达式;
点为反比例函数图像上一点,连接,若,求点的坐标.
13. 如图,在平面直角坐标系中,一次函数的图象与轴交于点,与反比例函数的图象交于,两点,点在第一象限,纵坐标为,点在第三象限,轴,垂足为点,.
求反比例函数和一次函数的解析式.
连接,,求四边形的面积.
14. 如图,一次函数与反比例函数的图象交于,两点,与轴相交于点.
求一次函数的表达式
求的面积
在直线上是否存在点,使得,若存在,求出点的坐标,若不存在,请说明理由.
15. 如图,一次函数、为常数,的图象与反比例函数为常数,的图象在第二象限交于点,与轴负半轴交于点,且.
求反比例函数和一次函数的表达式.
根据图象直接写出当时,不等式的解集.
16. 如图,直线与双曲线交于、两点,点的坐标为,经过点直线与轴交于点.
求反比例函数的表达式以及点的坐标;
点是轴上一动点,连接,若是的面积的一半,求此时点的坐标.
17. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于,两点.
求一次函数和反比例函数的解析式;
若点在轴上,位于原点右侧,且,求的面积.
18. 如图,直线与反比例函数的图象相交于点、,过点作轴,垂足为点,连接.
求反比例函数的解析式;
求;
利用函数图象直接写出关于的不等式的解集.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
