13.1三角形中的边角关系、命题与证明-三角形的三线 课件(共19张PPT) 2023--2024学年沪科版数学八年级上册
文档属性
| 名称 | 13.1三角形中的边角关系、命题与证明-三角形的三线 课件(共19张PPT) 2023--2024学年沪科版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 22:22:44 | ||
图片预览



文档简介
(共19张PPT)
三角形的三线
沪科版八年级上册数学
A
B
C
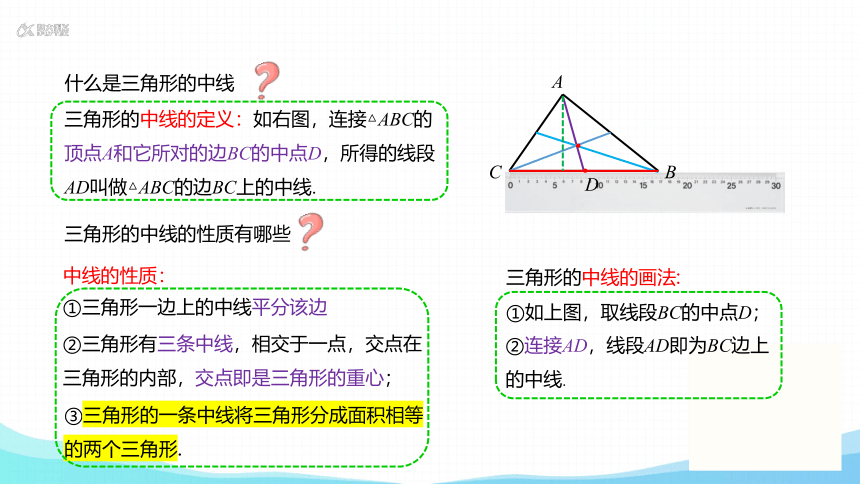
什么是三角形的中线
D
三角形的中线的定义:如右图,连接△ABC的顶点A和它所对的边BC的中点D,所得的线段AD叫做△ABC的边BC上的中线.
三角形的中线的画法:
①如上图,取线段BC的中点D;
②连接AD,线段AD即为BC边上的中线.
中线的性质:
①三角形一边上的中线平分该边
②三角形有三条中线,相交于一点,交点在三角形的内部,交点即是三角形的重心;
③三角形的一条中线将三角形分成面积相等的两个三角形.
.
.
三角形的中线的性质有哪些
什么是三角形的高线
A
B
C
三角形的高线的定义:如图,从△ABC的顶点A向它所对的边BC所在的直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高.
A
B
C
怎样作三角形的高线
D
D
高线的画法:①如图,将直角三角板的一条直角边与边BC所在的直线重合,并在直线BC上移动;
②当直角三角板的另一直角边经过点A时,过点A沿该直角边作直线,与直线BC交于点D,则线段AD即为△ABC的边BC上的高.
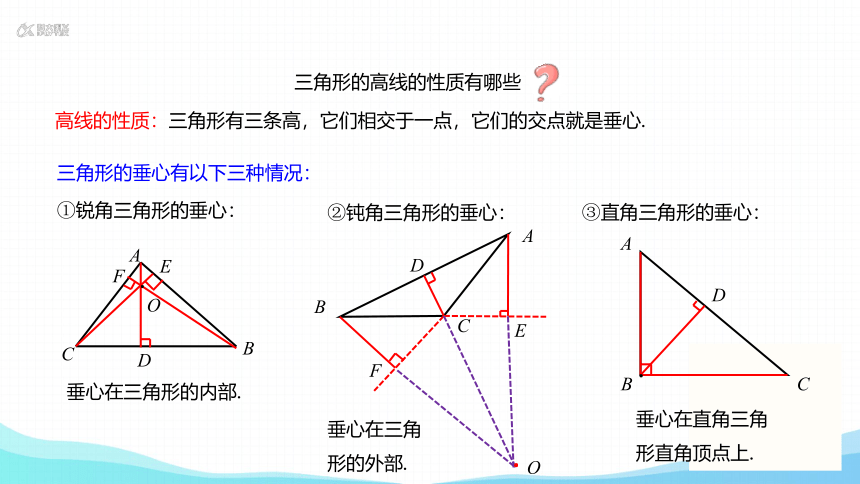
高线的性质:三角形有三条高,它们相交于一点,它们的交点就是垂心.
三角形的高线的性质有哪些
三角形的垂心有以下三种情况:
A
B
C
D
①锐角三角形的垂心:
F
E
.
O
垂心在三角形的内部.
②钝角三角形的垂心:
B
A
C
D
E
F
.
O
垂心在三角形的外部.
③直角三角形的垂心:
B
A
C
D
.
垂心在直角三角形直角顶点上.
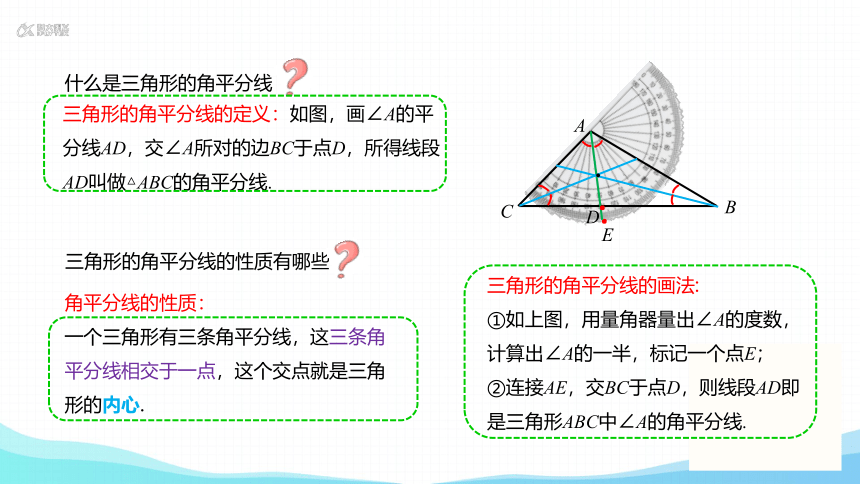
什么是三角形的角平分线
A
B
C
.
.
D
三角形的角平分线的定义:如图,画∠A的平分线AD,交∠A所对的边BC于点D,所得线段AD叫做△ABC的角平分线.
三角形的角平分线的画法:
①如上图,用量角器量出∠A的度数,计算出∠A的一半,标记一个点E;
②连接AE,交BC于点D,则线段AD即是三角形ABC中∠A的角平分线.
三角形的角平分线的性质有哪些
角平分线的性质:
一个三角形有三条角平分线,这三条角平分线相交于一点,这个交点就是三角形的内心.
E
.
三角形三条重要的线段的画法、性质
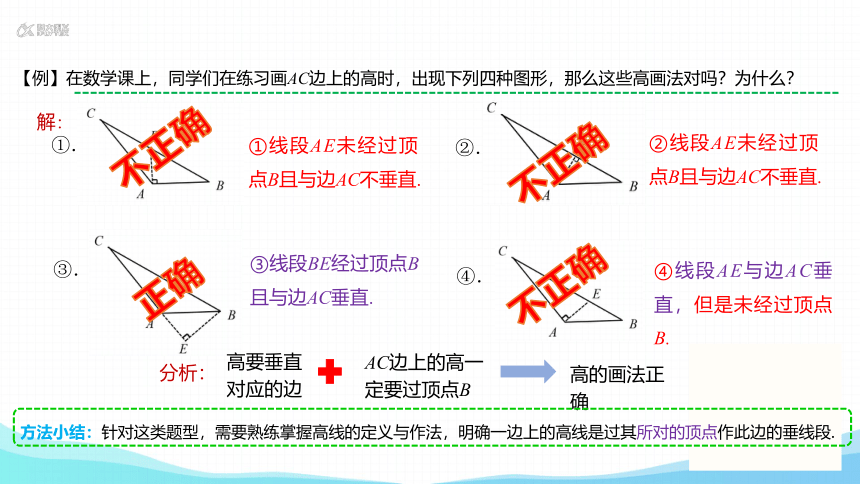
【例】在数学课上,同学们在练习画AC边上的高时,出现下列四种图形,那么这些高画法对吗?为什么?
分析:
①.
②.
③.
④.
高要垂直对应的边
AC边上的高一定要过顶点B
高的画法正确
解:
①线段AE未经过顶点B且与边AC不垂直.
②线段AE未经过顶点B且与边AC不垂直.
不正确
③线段BE经过顶点B且与边AC垂直.
正确
不正确
④线段AE与边AC垂直,但是未经过顶点B.
不正确
方法小结:针对这类题型,需要熟练掌握高线的定义与作法,明确一边上的高线是过其所对的顶点作此边的垂线段.
【例】给出下列说法:①三条线段组成的图形叫三角形;②三角形的角平分线是射线;③三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外;④任何一个三角形都有三条高、三条中线、三条角平分线;⑤三角形的三条角平分线交于一点,且这点在三角形内,正确的说法有 个.
分析:
解:
概念判断题
三线的基本定义
注意细节!
①由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫三角形,所以错误;
②三角形的角平分线是线段,不是射线,所以错误;
③三角形的高所在的直线交于一点,这个点叫三角形的垂心,直角三角形的垂心在直角三角形直角顶点上,所以错误;
④任何一个三角形都有三条高、三条中线、三条角平分线,所以正确;
⑤三角形的角平分线只能在三角形内,所以它们的交点在三角形内,所以正确.
√
√
方法小结:这类定义判断类问题,需要熟练的掌握相关的定义,注意关键字词有没有缺失即可.
2
【例】如图,已知AE是△ABC的边BC上的中线,若 , △ACE的周长比△AEB 的周长多2cm,则AC的长度是多少.
分析:
AE是中线
AE是公共边
两三角形的周长差就
是最后一边边长差
解:
∵AE是△ABC的边BC上的中线,
∴,
又∵AE是公共边,且
,
即,
所以,
即的长度为10cm.
方法小结:这类题型主要利用中线的性质,将周长的差转化为所求边长的差进行解题.
∴,
【例】在△ABC中,,,BC边上的高AD=8 ,则△ABC边AB上的 高是多少.
分析:
已知一边和一边上的高
求出面积
同一个三角形面积相同
利用等面积法求出AB边上的高
解:
设△ABC边AB上的高为h,
∵且BC边上的高AD=8,
∴,
∵, ,
∴,
所以△ABC边AB上的高是9.6.
方法小结:这类题目只要用等面积法去处理即可,同一个三角形面积相等,那么将另一个底边长代入面积计算公式即可求出另一边上的高.
三角形的中线与三角形的面积
【例】如图,在△ABC中,已知点D,E分别为边BC,AD的中点,且=,则△BCE的面积是多少?
分析:
点D,E是中点
AD,BE,
CE是中线
它们把对应三角形的面积2等分
解:
∵点D,E分别为边BC,AD的中点,
∴AD,BE,CE分别是△ ABC、 △ ABD和△ ACD的中线,
∴AD、BE和CE分别平分△ ABC、 △ ABD和△ ACD的面积,
∴ ,
∴ ,
∴ ,
∴ ,
∴△BCE的面积是.
方法总结:这类题型我们要先确定中点位置,找到中线和中线所在的三角形,根据中线和三角形的面积关系来计算各个小三角形的面积,再看要求的三角形是由哪几个小三角形构成的,求和即可.
计算各个小三角形面积,再去求△BCE的面积
三角形的中线与三角形的面积
【例】如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且=,则 ________.
分析:
点D,E,F
是中点
AD,BE,CE和BF是中线
各个三角形的面积2等分,从而计算出各个小三角形面积
求和即得到△ BCE的面积
阴影部分面积即为△BCE的面积的一半
解:
∵点D,E,F分别为边BC,AD和CE的中点,
∴AD,BE,CE,BF分别是△ABC、 △ ABD、△ACD和△BCE的中线,
∴AD、BE,CE ,BF分别平分△ABC、△ABD、△ACD和△BCE的面积,
∴ ,
∴ ,
∴ ,
∴ ,
∴,
∴阴影部分的面积为1 .
1
方法总结:遇到这类问题,先明确中点所在的位置,以及构成的中线位于哪个三角形中,再根据三角形的中线和三角形面积的关系计算出各个三角形的面积,最后找到所求图形的面积与已知面积之间的关系即可求解.
【例】如图,在△ABC中,点D是BC边上任意一点,点E,F,G分别为边AD,BE,CE的中点,则________
分析:
点E,F,G分别为边AD,BE,CE的中点
中线平分三
角形面积
面积未知,不妨设两个面积
表示出各个部分面积,求比值
解:
∵点E,F,G分别为边AD,BE,CE的中点,
∴DF,BE,CE,DG分别是△BDE、 △ ABD、△ACD和△CDE的中线,
∴DF,BE,CE,DG分别平分△BDE、 △ ABD、△ACD和△CDE的面积,
设△ABD的面积为x,△ACD的面积为y,
那么△ABC的面积为(x+y),
∴ , ,
∴ , ,
面积
∴EFDG的面积为(),
∴(): (x+y) =1:4.
方法总结:求面积的比值问题,若题目中没有给出具体的数据,我们可以直接设出关键三角形的面积,利用三角形中线的性质,表示出其它三角形的面积,最终得出所求面积比.
1:4
三角形的三线三心
定义:三角形中,连接一个顶点和它对边的中点的连线段叫做三角形的中线.
三角形的中线将一个三角形分成面积相等的两个三角形.
中线
角平分线
高线
定义:三角形的一个角的平分线与这个内角的对边相交,连接这个角的顶点和交点的线段叫三角形的角平分线.
定义:从三角形一个顶点向它的对边(或对边所在的直线)作垂线,那么这个顶点和垂足间的线段叫做三角形的高线.
重心:三角形三条中线的交点.
内心:三角形三条角平分线的交点.
垂心:三角形三条高线的交点.锐角三角形的垂心在它的内部,钝角三角形的垂心在它的外部,直角三角形的垂心在它的直角顶点上.
方法总结
三角形三条重要线段的画法和性质
三角形的中线与三角形的面积
要牢记三角形三线的画法和性质,利用三角形三线的性质去解决周长问题,证明问题等.
三角形的中线与面积问题要熟练掌握三角形的中线的性质,中线可以将三角形面积等分,推论出线段等分点可以等分三角形面积,找到要求的面积是由哪些部分组成求和即可.
再 见
三角形的三线
沪科版八年级上册数学
A
B
C
什么是三角形的中线
D
三角形的中线的定义:如右图,连接△ABC的顶点A和它所对的边BC的中点D,所得的线段AD叫做△ABC的边BC上的中线.
三角形的中线的画法:
①如上图,取线段BC的中点D;
②连接AD,线段AD即为BC边上的中线.
中线的性质:
①三角形一边上的中线平分该边
②三角形有三条中线,相交于一点,交点在三角形的内部,交点即是三角形的重心;
③三角形的一条中线将三角形分成面积相等的两个三角形.
.
.
三角形的中线的性质有哪些
什么是三角形的高线
A
B
C
三角形的高线的定义:如图,从△ABC的顶点A向它所对的边BC所在的直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高.
A
B
C
怎样作三角形的高线
D
D
高线的画法:①如图,将直角三角板的一条直角边与边BC所在的直线重合,并在直线BC上移动;
②当直角三角板的另一直角边经过点A时,过点A沿该直角边作直线,与直线BC交于点D,则线段AD即为△ABC的边BC上的高.
高线的性质:三角形有三条高,它们相交于一点,它们的交点就是垂心.
三角形的高线的性质有哪些
三角形的垂心有以下三种情况:
A
B
C
D
①锐角三角形的垂心:
F
E
.
O
垂心在三角形的内部.
②钝角三角形的垂心:
B
A
C
D
E
F
.
O
垂心在三角形的外部.
③直角三角形的垂心:
B
A
C
D
.
垂心在直角三角形直角顶点上.
什么是三角形的角平分线
A
B
C
.
.
D
三角形的角平分线的定义:如图,画∠A的平分线AD,交∠A所对的边BC于点D,所得线段AD叫做△ABC的角平分线.
三角形的角平分线的画法:
①如上图,用量角器量出∠A的度数,计算出∠A的一半,标记一个点E;
②连接AE,交BC于点D,则线段AD即是三角形ABC中∠A的角平分线.
三角形的角平分线的性质有哪些
角平分线的性质:
一个三角形有三条角平分线,这三条角平分线相交于一点,这个交点就是三角形的内心.
E
.
三角形三条重要的线段的画法、性质
【例】在数学课上,同学们在练习画AC边上的高时,出现下列四种图形,那么这些高画法对吗?为什么?
分析:
①.
②.
③.
④.
高要垂直对应的边
AC边上的高一定要过顶点B
高的画法正确
解:
①线段AE未经过顶点B且与边AC不垂直.
②线段AE未经过顶点B且与边AC不垂直.
不正确
③线段BE经过顶点B且与边AC垂直.
正确
不正确
④线段AE与边AC垂直,但是未经过顶点B.
不正确
方法小结:针对这类题型,需要熟练掌握高线的定义与作法,明确一边上的高线是过其所对的顶点作此边的垂线段.
【例】给出下列说法:①三条线段组成的图形叫三角形;②三角形的角平分线是射线;③三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外;④任何一个三角形都有三条高、三条中线、三条角平分线;⑤三角形的三条角平分线交于一点,且这点在三角形内,正确的说法有 个.
分析:
解:
概念判断题
三线的基本定义
注意细节!
①由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫三角形,所以错误;
②三角形的角平分线是线段,不是射线,所以错误;
③三角形的高所在的直线交于一点,这个点叫三角形的垂心,直角三角形的垂心在直角三角形直角顶点上,所以错误;
④任何一个三角形都有三条高、三条中线、三条角平分线,所以正确;
⑤三角形的角平分线只能在三角形内,所以它们的交点在三角形内,所以正确.
√
√
方法小结:这类定义判断类问题,需要熟练的掌握相关的定义,注意关键字词有没有缺失即可.
2
【例】如图,已知AE是△ABC的边BC上的中线,若 , △ACE的周长比△AEB 的周长多2cm,则AC的长度是多少.
分析:
AE是中线
AE是公共边
两三角形的周长差就
是最后一边边长差
解:
∵AE是△ABC的边BC上的中线,
∴,
又∵AE是公共边,且
,
即,
所以,
即的长度为10cm.
方法小结:这类题型主要利用中线的性质,将周长的差转化为所求边长的差进行解题.
∴,
【例】在△ABC中,,,BC边上的高AD=8 ,则△ABC边AB上的 高是多少.
分析:
已知一边和一边上的高
求出面积
同一个三角形面积相同
利用等面积法求出AB边上的高
解:
设△ABC边AB上的高为h,
∵且BC边上的高AD=8,
∴,
∵, ,
∴,
所以△ABC边AB上的高是9.6.
方法小结:这类题目只要用等面积法去处理即可,同一个三角形面积相等,那么将另一个底边长代入面积计算公式即可求出另一边上的高.
三角形的中线与三角形的面积
【例】如图,在△ABC中,已知点D,E分别为边BC,AD的中点,且=,则△BCE的面积是多少?
分析:
点D,E是中点
AD,BE,
CE是中线
它们把对应三角形的面积2等分
解:
∵点D,E分别为边BC,AD的中点,
∴AD,BE,CE分别是△ ABC、 △ ABD和△ ACD的中线,
∴AD、BE和CE分别平分△ ABC、 △ ABD和△ ACD的面积,
∴ ,
∴ ,
∴ ,
∴ ,
∴△BCE的面积是.
方法总结:这类题型我们要先确定中点位置,找到中线和中线所在的三角形,根据中线和三角形的面积关系来计算各个小三角形的面积,再看要求的三角形是由哪几个小三角形构成的,求和即可.
计算各个小三角形面积,再去求△BCE的面积
三角形的中线与三角形的面积
【例】如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且=,则 ________.
分析:
点D,E,F
是中点
AD,BE,CE和BF是中线
各个三角形的面积2等分,从而计算出各个小三角形面积
求和即得到△ BCE的面积
阴影部分面积即为△BCE的面积的一半
解:
∵点D,E,F分别为边BC,AD和CE的中点,
∴AD,BE,CE,BF分别是△ABC、 △ ABD、△ACD和△BCE的中线,
∴AD、BE,CE ,BF分别平分△ABC、△ABD、△ACD和△BCE的面积,
∴ ,
∴ ,
∴ ,
∴ ,
∴,
∴阴影部分的面积为1 .
1
方法总结:遇到这类问题,先明确中点所在的位置,以及构成的中线位于哪个三角形中,再根据三角形的中线和三角形面积的关系计算出各个三角形的面积,最后找到所求图形的面积与已知面积之间的关系即可求解.
【例】如图,在△ABC中,点D是BC边上任意一点,点E,F,G分别为边AD,BE,CE的中点,则________
分析:
点E,F,G分别为边AD,BE,CE的中点
中线平分三
角形面积
面积未知,不妨设两个面积
表示出各个部分面积,求比值
解:
∵点E,F,G分别为边AD,BE,CE的中点,
∴DF,BE,CE,DG分别是△BDE、 △ ABD、△ACD和△CDE的中线,
∴DF,BE,CE,DG分别平分△BDE、 △ ABD、△ACD和△CDE的面积,
设△ABD的面积为x,△ACD的面积为y,
那么△ABC的面积为(x+y),
∴ , ,
∴ , ,
面积
∴EFDG的面积为(),
∴(): (x+y) =1:4.
方法总结:求面积的比值问题,若题目中没有给出具体的数据,我们可以直接设出关键三角形的面积,利用三角形中线的性质,表示出其它三角形的面积,最终得出所求面积比.
1:4
三角形的三线三心
定义:三角形中,连接一个顶点和它对边的中点的连线段叫做三角形的中线.
三角形的中线将一个三角形分成面积相等的两个三角形.
中线
角平分线
高线
定义:三角形的一个角的平分线与这个内角的对边相交,连接这个角的顶点和交点的线段叫三角形的角平分线.
定义:从三角形一个顶点向它的对边(或对边所在的直线)作垂线,那么这个顶点和垂足间的线段叫做三角形的高线.
重心:三角形三条中线的交点.
内心:三角形三条角平分线的交点.
垂心:三角形三条高线的交点.锐角三角形的垂心在它的内部,钝角三角形的垂心在它的外部,直角三角形的垂心在它的直角顶点上.
方法总结
三角形三条重要线段的画法和性质
三角形的中线与三角形的面积
要牢记三角形三线的画法和性质,利用三角形三线的性质去解决周长问题,证明问题等.
三角形的中线与面积问题要熟练掌握三角形的中线的性质,中线可以将三角形面积等分,推论出线段等分点可以等分三角形面积,找到要求的面积是由哪些部分组成求和即可.
再 见
