2023年海南省临高县中考模拟预测数学试题(含解析)
文档属性
| 名称 | 2023年海南省临高县中考模拟预测数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 422.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 23:43:05 | ||
图片预览

文档简介
2023年海南省临高县中考模拟预测数学试题
一、选择题(本大题满分36分,每小题3分)在下列各题的四个备选答案中,有且只有一个是正确的。
1.在0,﹣2,1,这四个数中( )
A.0 B.1 C.﹣2 D.
2.计算m2 m3的结果是( )
A.6m B.5m C.m6 D.m5
3.中国信息通信研究院发布预测称,2025年中国5G用户规模将超过858000000人.将数据858000000用科学记数法表示为( )
A.8.58×1010 B.8.58×109 C.8.58×108 D.8.58×107
4.如图是由5个大小相同的小正方体摆成的立体图形,它的主视图是( )
A. B.
C. D.
5.要使分式有意义,则x应满足的条件是( )
A.x≠1 B.x≠1或x≠0 C.x≠0 D.x>1
6.如图,已知AB∥CD,∠1=115°,则∠C等于( )
A.40° B.45° C.50° D.65°
7.如图,AD是△ABC的中线,若AB=8,AC=6,则AD等于( )
A.4 B.5 C.6 D.7
8.如图,在菱形ABCD中,AC=8,则△ABD的周长等于( )
A.20 B.18 C.16 D.14
9.已知点A(a,4)在双曲线上,则a的值是( )
A.4 B.﹣4 C.1 D.﹣1
10.随机掷一枚质地均匀的普通硬币两次,出现两次正面都朝上的概率是( )
A. B. C. D.
11.如图,⊙O的直径AB为3,点B为OD的中点,则AC的长为( )
A.2 B. C. D.
12.如图1,在矩形ABCD中,动点P从点B出发,设点P运动的路程为x,△ABP的面积为y,函数的图象如图2所示,则△ABC的面积为( )
A.15 B.16 C.20 D.30
二、填空题(本大题满分12分,每小题3分)
13.因式分解:x2+4y2﹣4xy= .
14.分式方程=3的解是 .
15.如图,在△ABC中,DE∥AC,DE=2,则AC= .
16.将矩形ABCD纸片按如图所示方式折叠,M、N分别为AB、CD的中点,点B的对应点B'恰好落在MN上.若AB=10,则DN的长为 ,折痕AE长为 .
三、解答题(本大题满分72分
17.(12分)(1)计算:(﹣1)2023+18÷(﹣)﹣2﹣×;
(2)求不等式组的所有整数解.
18.(10分)王阿姨去买水果,3kg芒果和2kg香蕉应付40元,可她把两种水果的单价弄反了
19.(10分)某中学初一年级刚搬迁到离市区较远的新校区,学校为了了解学生周末回家方式,从乘车、步行、骑车三个方面随机对该年级部分学生周末回家方式进行了一次调查统计(图1和图2),请你根据图中提供的信息解答下列问题:
(1)该学校采取的调查方式是 (填写“普查”或“抽样调查”);
(2)本次一共调查了 名学生,图1条形统计图中m= ;
(3)估计全年级860名学生中步行的有 人;
(4)预计今年秋季该校初一年级招生将增加10%,到时乘车回家人数约增加 人.
20.(10分)如图,在坡顶A处的同一水平面上有一座古塔BC(BC⊥AC),数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处又测得该塔的塔顶B的仰角为76°.
(1)填空:∠ABC= 度,∠PBC= 度;
(2)求坡顶A到地面PQ的距离;
(3)求古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4)
21.(15分)如图,在矩形ABCD中,AB=5,点E是边CD上一动点(点E不与C、D重合),延长DC到点F,连接AF与BE交于点G,AF与BC交于点H,BF.
(1)求证:①△ABG≌△FEG;②AE∥BF;
(2)若AG=AB,求线段GH的长;
(3)点E在运动过程中,△FEG的面积大小是否发生改变?若改变,请说明理由,请求出△FEG的面积.
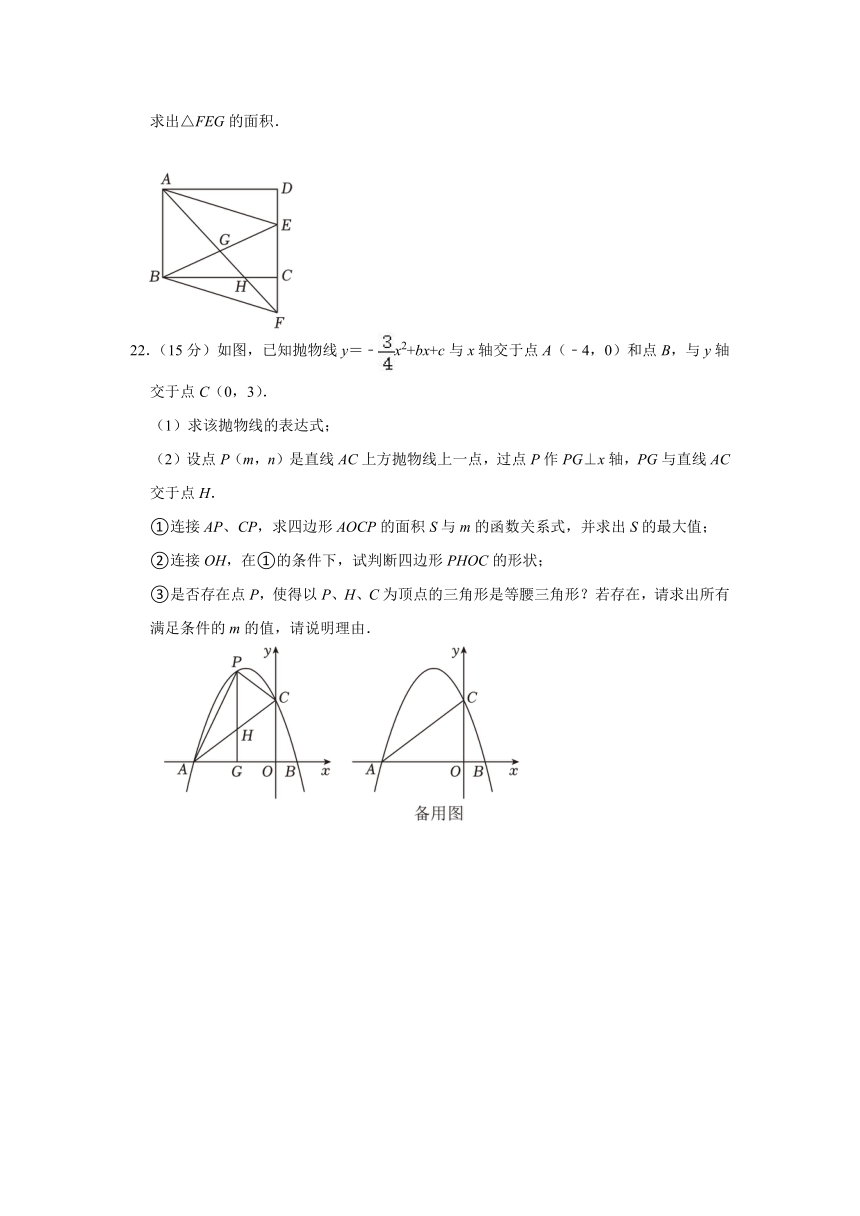
22.(15分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣4,0)和点B,与y轴交于点C(0,3).
(1)求该抛物线的表达式;
(2)设点P(m,n)是直线AC上方抛物线上一点,过点P作PG⊥x轴,PG与直线AC交于点H.
①连接AP、CP,求四边形AOCP的面积S与m的函数关系式,并求出S的最大值;
②连接OH,在①的条件下,试判断四边形PHOC的形状;
③是否存在点P,使得以P、H、C为顶点的三角形是等腰三角形?若存在,请求出所有满足条件的m的值,请说明理由.
2023年海南省临高县中考数学模拟试卷
参考答案与试题解析
一、选择题(本大题满分36分,每小题3分)在下列各题的四个备选答案中,有且只有一个是正确的。
1.在0,﹣2,1,这四个数中( )
A.0 B.1 C.﹣2 D.
【分析】根据正数大于负数,两个负数比较大小,绝对值大的负数反而小,可得答案.
【解答】解:∵﹣2<0<<1,
∴最小的数是﹣2,
故选:C.
【点评】本题考查了有理数大小比较,两个负数比较大小,绝对值大的负数反而小.
2.计算m2 m3的结果是( )
A.6m B.5m C.m6 D.m5
【分析】根据同底数幂的乘法法则计算即可.
【解答】解:原式=m2+3
=m6,
故选:D.
【点评】本题考查了同底数幂的乘法,掌握am an=am+n是解题的关键.
3.中国信息通信研究院发布预测称,2025年中国5G用户规模将超过858000000人.将数据858000000用科学记数法表示为( )
A.8.58×1010 B.8.58×109 C.8.58×108 D.8.58×107
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数,当原数绝对值<1时,n是负整数.
【解答】解:将数据858000000用科学记数法表示为8.58×108.
故选:C.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
4.如图是由5个大小相同的小正方体摆成的立体图形,它的主视图是( )
A. B.
C. D.
【分析】找到从正面看所得到的图形即可.
【解答】解:从物体正面看,左边2个正方形.
故选:A.
【点评】本题考查了简单组合体的三视图,主视图是从物体的正面看得到的视图,解答时学生易将三种视图混淆而错误的选其它选项.
5.要使分式有意义,则x应满足的条件是( )
A.x≠1 B.x≠1或x≠0 C.x≠0 D.x>1
【分析】根据分式的分母不为零分式有意义,可得答案.
【解答】解:由分式有意义,得
x﹣1≠8,
解得x≠1.
故选:A.
【点评】本题考查了分式有意义的条件,分母不等于零分式有意义.
6.如图,已知AB∥CD,∠1=115°,则∠C等于( )
A.40° B.45° C.50° D.65°
【分析】根据平行线的性质得出∠3=115°,再根据三角形外角性质求解即可.
【解答】解:如图,
∵AB∥CD,∠1=115°,
∴∠1=∠3=115°,
∵∠3=∠C+∠2,∠5=65°,
∴∠C=50°,
故选:C.
【点评】此题考查了平行线的性质及三角形外角性质,熟记“两直线平行,同位角相等”是解题的关键.
7.如图,AD是△ABC的中线,若AB=8,AC=6,则AD等于( )
A.4 B.5 C.6 D.7
【分析】首先根据勾股定理逆定理可得△ABC是直角三角形,再根据直角三角形的性质:在直角三角形中,斜边上的中线等于斜边的一半可得AD=BC=5.
【解答】解:∵62+82=102,
∴△ABC是直角三角形,
∵AD是△ABC的中线,
∴AD=BC=5,
故选:B.
【点评】此题主要考查了直角三角形的性质以及勾股定理逆定理,关键是掌握在直角三角形中,斜边上的中线等于斜边的一半.
8.如图,在菱形ABCD中,AC=8,则△ABD的周长等于( )
A.20 B.18 C.16 D.14
【分析】根据菱形对角线互相垂直平分的性质,可以求得BO=OD,AO=OC,在Rt△AOD中,根据勾股定理可以求得AB的长,进而△ABD的周长.
【解答】解:菱形对角线互相垂直平分,
∴BO=OD=3,AO=OC=4,
∴AB=3,
∴△ABD的周长等于5+5+5=16,
故选:C.
【点评】本题考查了菱形面积的计算,考查了勾股定理在直角三角形中的运用,考查了菱形各边长相等的性质,本题中根据勾股定理计算AB的长是解题的关键.
9.已知点A(a,4)在双曲线上,则a的值是( )
A.4 B.﹣4 C.1 D.﹣1
【分析】把点A(a,4)代入即可得到结论.
【解答】解:∵点A(a,4)在双曲线上,
∴3=﹣,
∴a=﹣1,
故选:D.
【点评】本题考查了反比例函数的性质,反比例函数图形上点的坐标特征,熟练掌握反比例函数的性质是解题的关键.
10.随机掷一枚质地均匀的普通硬币两次,出现两次正面都朝上的概率是( )
A. B. C. D.
【分析】依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率即可解答.
【解答】解:画树状图如下:
共有4种等可能的结果,两次正面都朝上的情况有1种.
故选:B.
【点评】本题考查的是用列表法或画树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;用到的知识点为:概率=所求情况数与总情况数之比.
11.如图,⊙O的直径AB为3,点B为OD的中点,则AC的长为( )
A.2 B. C. D.
【分析】根据切线的性质可得∠OCD=90°,再根据线段的中点定义可得OD=2OB,从而可得OD=AB=3,然后在Rt△DOC中,利用锐角三角函数的定义可得sinD=,从而可得∠D=30°,进而利用直角三角形的边角关系可得OC=,DC=,∠DOC=60°,最后利用圆周角定理可得∠A=30°,从而可得∠D=∠A=30°,从而利用等角对等边可得DC=AC=,即可解答.
【解答】解:∵DC切⊙O于点C,
∴∠OCD=90°,
∵点B为OD的中点,
∴OD=2OB,
∵AB=2OB,
∴OD=AB=7,
在Rt△DOC中,OD=2OC=3,
∴sinD==,
∴∠D=30°,
∴OC=OD=OC=,
∴∠A=∠DOC=30°,
∴∠D=∠A=30°,
∴DC=AC=,
故选:D.
【点评】本题考查了切线的性质,圆周角定理,解直角三角形,熟练掌握切线的性质,以及圆周角定理是解题的关键.
12.如图1,在矩形ABCD中,动点P从点B出发,设点P运动的路程为x,△ABP的面积为y,函数的图象如图2所示,则△ABC的面积为( )
A.15 B.16 C.20 D.30
【分析】解本题需注意一定的面积值相对应的距离可以有2个.找到对应的点,找出准确反映y与x之间对应关系的图象,需分析在不同阶段中y随x变化的情况.
【解答】解:由图2知:
当动点P由B→C时,点P运动的路程为5,
∴BC=2,
当x=5和x=11时,△ABP的面积相等,
∴CD=6,
∴S△ABC=CD×BC=15,
故选:A.
【点评】解决本题的关键是读懂图意,得到相应的矩形中各边之间的关系.此题考查了学生从图象中读取信息的数形结合能力.
二、填空题(本大题满分12分,每小题3分)
13.因式分解:x2+4y2﹣4xy= (x﹣2y)2 .
【分析】直接利用完全平方公式进行分解即可.
【解答】解:原式=x2﹣4xy+4y2=(x﹣2y)5,
故答案为:(x﹣2y)2.
【点评】此题主要考查了公式法分解因式,关键是掌握完全平方公式:a2±2ab+b2=(a±b)2.
14.分式方程=3的解是 x=3 .
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
【解答】解:去分母得:2x=3x﹣4,
解得:x=3,
经检验x=3是分式方程的解.
故答案为:x=4
【点评】此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.
15.如图,在△ABC中,DE∥AC,DE=2,则AC= 5 .
【分析】根据相似三角形的判定和性质即可求得答案.
【解答】解:∵=,
∴=,
∵DE∥AC,
∴△BDE∽△BAC,
∴=,
∴=,
∴AC=5.
故答案为:7.
【点评】本题主要考查了相似三角形的判定和性质,熟知相似三角形的判定和性质是解决问题的关键.
16.将矩形ABCD纸片按如图所示方式折叠,M、N分别为AB、CD的中点,点B的对应点B'恰好落在MN上.若AB=10,则DN的长为 5 ,折痕AE长为 .
【分析】连接BB′,由AE垂直平分BB′,得AB′=AB,由矩形的性质得CD∥AB,CD=AB=10,∠ABC=90°,因为M、N分别为AB、CD的中点,所以AM∥DN,AM=DN=5,可证明四边形AMND是矩形,MN垂直平分AB,则BB′=AB′=AB,所以∠BAB′=60°,∠BAE=∠B′AE=∠BAB′=30°,则BE=AE,所以AB==AE=10,则AE=,于是得到问题的答案.
【解答】解:连接BB′,
由折叠得,点B′与点B关于直线AE对称,
∴AE垂直平分BB′,
∴AB′=AB,
∵四边形ABCD是矩形,AB=10,
∴CD∥AB,CD=AB=10,
∵M、N分别为AB,
∴AM∥DN,AM=DN=5,
∴四边形AMND是平行四边形,
∵∠D=90°,
∴四边形AMND是矩形,
∴∠AMN=90°,
∴MN垂直平分AB,
∴BB′=AB′=AB,
∴∠BAB′=60°,
∴∠BAE=∠B′AE=∠BAB′=30°,
∴BE=AE,
∴AB===AE,
∴AE=10,
解得AE=,
故答案为:2,.
【点评】此题重点考查矩形的判定与性质、轴对称的性质、线段的垂直平分线的性质、等边三角形的判定与性质、直角三角形中30°角所对的直角边等于斜边的一半等知识,证明BB′=AB′=AB是解题的关键.
三、解答题(本大题满分72分
17.(12分)(1)计算:(﹣1)2023+18÷(﹣)﹣2﹣×;
(2)求不等式组的所有整数解.
【分析】(1)原式利用乘方的意义,负整数指数幂法则,二次根式的乘法法则计算即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分确定出不等式组的解集,即可求出所有整数解.
【解答】解:(1)原式=﹣1+18÷9﹣
=﹣6+2﹣3
=﹣3;
(2),
解不等式①,得x<2;
解不等式②,得 ;
该不等式组的解集是:,
所以,该不等式组所有整数解为:﹣2,0,5.
【点评】此题考查了实数的运算,解一元一次不等式组,熟练掌握不等式组的解法是解本题的关键.
18.(10分)王阿姨去买水果,3kg芒果和2kg香蕉应付40元,可她把两种水果的单价弄反了
【分析】设王阿姨买的芒果的单价为x元/kg,香蕉的单价为y元/kg,根据“3kg芒果和2kg香蕉应付40元,2kg芒果和3kg香蕉应付35元”,可列出关于x,y的二元一次方程组,解之即可得出结论.
【解答】解:设王阿姨买的芒果的单价为x元/kg,香蕉的单价为y元/kg,
根据题意得:,
解得:.
答:王阿姨买的芒果的单价为10元/kg,香蕉的单价为5元/kg.
【点评】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
19.(10分)某中学初一年级刚搬迁到离市区较远的新校区,学校为了了解学生周末回家方式,从乘车、步行、骑车三个方面随机对该年级部分学生周末回家方式进行了一次调查统计(图1和图2),请你根据图中提供的信息解答下列问题:
(1)该学校采取的调查方式是 抽样调查 (填写“普查”或“抽样调查”);
(2)本次一共调查了 60 名学生,图1条形统计图中m= 12 ;
(3)估计全年级860名学生中步行的有 172 人;
(4)预计今年秋季该校初一年级招生将增加10%,到时乘车回家人数约增加 43 人.
【分析】(1)根据普查和抽样调查的定义解答即可;
(2)用“骑车”的人数除以30%可得样本容量,再用样本容量分别减去其他两种方式的人数可得m的值;
(3)用全年级人数乘样本值“步行”所占比例即可;
(4)根据题意列式计算即可得到结论.
【解答】解:(1)该学校采取的调查方式是抽样调查,
故答案为:抽样调查;
(2)本次一共调查了学生:18÷30%=60(名),
∴m=60﹣30﹣18=12.
故答案为:60,12;
(3)估计全年级860名学生中步行的有:860×=172(人),
故答案为:172;
(4)预计今年秋季该校初一年级招生将增加10%,到时乘车回家人数约增加:860×10%×,
故答案为:43.
【点评】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
20.(10分)如图,在坡顶A处的同一水平面上有一座古塔BC(BC⊥AC),数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处又测得该塔的塔顶B的仰角为76°.
(1)填空:∠ABC= 14 度,∠PBC= 45 度;
(2)求坡顶A到地面PQ的距离;
(3)求古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4)
【分析】(1)延长BC交PQ于点D,根据题意可得:∠BPD=45°,∠BAC=76°,BD⊥PQ,从而可得∠BDP=90°,然后利用直角三角形的两个锐角互余可得∠PBC=45°,再根据垂直定义可得∠BCA=90°,从而利用直角三角形的两个锐角互余可得∠ABC=14°,即可解答;
(2)过点A作AE⊥PQ,垂足为E,根据已知可设AE=5k米,则PE=12k米,然后在Rt△AEP中,利用勾股定理进行计算,即可解答;
(3)根据题意可得:CD=AE=10米,AC=DE,然后设AC=DE=y米,则DP=(y+24)米,然后在Rt△BDP中,利用锐角三角函数的定义求出BD的长,再在Rt△ABC中,利用锐角三角函数的定义求出BC的长,从而求出BD的长,最后列出关于y的方程,进行计算即可解答.
【解答】解:(1)延长BC交PQ于点D,
由题意得:∠BPD=45°,∠BAC=76°,
∴∠BDP=90°,
∴∠PBC=90°﹣∠BPD=45°,
∵BC⊥AC,
∴∠BCA=90°,
∴∠ABC=90°﹣∠BAC=14°,
故答案为:14;45;
(2)过点A作AE⊥PQ,垂足为E,
∵斜坡AP的坡度i=1:2.4,
∴==,
∴设AE=5k米,则PE=12k米,
在Rt△AEP中,AP==,
∵AP=26米,
∴13k=26,
解得:k=2,
∴AE=10米,PE=24米,
∴坡顶A到地面PQ的距离为10米;
(3)由题意得:CD=AE=10米,AC=DE,
设AC=DE=y米,
∵PE=24米,
∴PD=DE+PE=(y+24)米,
在Rt△BDP中,∠BPD=45°,
∴BD=PD tan45°=(y+24)米,
在Rt△ABC中,∠BAC=76°,
∴BC=AC tan76°≈2y(米),
∴BD=BC+CD=(4y+10)米,
∴y+24=4y+10,
解得:y=,
∴BC=4y≈19(米),
∴古塔BC的高度约为19米.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,坡度坡角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
21.(15分)如图,在矩形ABCD中,AB=5,点E是边CD上一动点(点E不与C、D重合),延长DC到点F,连接AF与BE交于点G,AF与BC交于点H,BF.
(1)求证:①△ABG≌△FEG;②AE∥BF;
(2)若AG=AB,求线段GH的长;
(3)点E在运动过程中,△FEG的面积大小是否发生改变?若改变,请说明理由,请求出△FEG的面积.
【分析】(1)①根据矩形的性质及全等三角形的判定即可证得.
②根据平行四边形的判定即可证得.
(2)根据矩形的性质和勾股定理求出DF,得到,求出HF,即可求解.
(3)过点G作GP⊥EF于点P,证明GP是△ADF 的中位线,求出GP,即可求解.
【解答】(1)证明:①∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,
∴∠BAG=∠EFG.
∵CF=DE,
∴CF+CE=DE+CE,
即EF=CD=AB.
又∵∠AGB=∠EGF,
∴△ABG≌△FEG(AAS).
②∵AB∥EF,AB=EF,
∴四边形ABEF是平行四边形,
∴AE∥BF.
(2)解:∵△ABG≌△FEG,
∴GF=AF=AB=5,
∴AF=10,
在矩形ABCD中,AD=BC=6,
在Rt△ADC中,DF=,
∴CF=DF﹣CD=4.
在矩形ABCD中,CH∥AD,
∴,
即,
解得,
∴GH=GF﹣HF=.
(3)解:△FEG的面积大小不变.
如图,过点G作GP⊥EF于点P,
则GP∥AD,
∵GF=AG,
∴DP=FP,
∴GP是△ADF 的中位线,
∴,
∴S△FEG=.
【点评】本题考查了四边形的综合应用,解题关键是掌握全等三角形的性质与判定,勾股定理,矩形的性质.
22.(15分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣4,0)和点B,与y轴交于点C(0,3).
(1)求该抛物线的表达式;
(2)设点P(m,n)是直线AC上方抛物线上一点,过点P作PG⊥x轴,PG与直线AC交于点H.
①连接AP、CP,求四边形AOCP的面积S与m的函数关系式,并求出S的最大值;
②连接OH,在①的条件下,试判断四边形PHOC的形状;
③是否存在点P,使得以P、H、C为顶点的三角形是等腰三角形?若存在,请求出所有满足条件的m的值,请说明理由.
【分析】(1)由待定系数法即可求解;
(2)①由S=S△AOC+S△AHP+S△CHP=,即可求解;
②由,即可求解;
③分HP=HC、CP=CH、PC=PH三种情况分别求解即可.
【解答】解:(1)由题意得:,
解得:,
则抛物线的表达式为:y=﹣;
(2)①∵A(﹣4,0),6),
设直线AC的表达式为:y=kx+3,
将点A的坐标代入上式得:0=﹣3k+3,
解得:k=,
∴直线AC的解析式为 ,
设点P的坐标为 ,故点H的坐标为 ,
则 .
∴四边形AOCP的面积S与m的函数关系式为:
S=S△AOC+S△AHP+S△CHP
=
=.
∵,﹣4<m<0,
∴当m=﹣8时,S有最大值;
②四边形PHOC是平行四边形,理由如下:
由①可得,当 m=﹣2 时,.
∵PH∥OC,
∴四边形PHOC是平行四边形;
③存在,理由如下:
∵点P的坐标为 ,点H的坐标为 ,
∴点G的坐标为(m,0),
则,OG=﹣m.
∵OA=4,OC=5,
∴AC=5.
∵PH∥OC,
,即
分三种情况讨论:
Ⅰ.当HP=HC时,
则 ,
解得:m=﹣或0 (舍去2).
Ⅱ.当 CP=CH 时,过点C作 CD⊥PH 于点D,
则 ,
∵DH+HG=DG=OC=8,
,
解得:m=﹣2或7 (0舍去).
Ⅲ.当 PC=PH 时,过点P作 PE⊥AC 于点E,
则
∠PEH=∠AGH=90°,∠PHE=∠AHG,
∴△PEH∽△AGH,
∴∠EPH=∠HAG,
∴sin∠EPH=sin∠HAG,
即 ,
,
解得:m=﹣或0 (舍去0),
综上所述,满足条件的m的值为 .
【点评】此题是二次函数的综合题,是中考的压轴题,难度较大,计算量也大,主要考查了待定系数法求解析式,还考查了三角形相似,平行四边形的性质等,分类求解是解决问题.
一、选择题(本大题满分36分,每小题3分)在下列各题的四个备选答案中,有且只有一个是正确的。
1.在0,﹣2,1,这四个数中( )
A.0 B.1 C.﹣2 D.
2.计算m2 m3的结果是( )
A.6m B.5m C.m6 D.m5
3.中国信息通信研究院发布预测称,2025年中国5G用户规模将超过858000000人.将数据858000000用科学记数法表示为( )
A.8.58×1010 B.8.58×109 C.8.58×108 D.8.58×107
4.如图是由5个大小相同的小正方体摆成的立体图形,它的主视图是( )
A. B.
C. D.
5.要使分式有意义,则x应满足的条件是( )
A.x≠1 B.x≠1或x≠0 C.x≠0 D.x>1
6.如图,已知AB∥CD,∠1=115°,则∠C等于( )
A.40° B.45° C.50° D.65°
7.如图,AD是△ABC的中线,若AB=8,AC=6,则AD等于( )
A.4 B.5 C.6 D.7
8.如图,在菱形ABCD中,AC=8,则△ABD的周长等于( )
A.20 B.18 C.16 D.14
9.已知点A(a,4)在双曲线上,则a的值是( )
A.4 B.﹣4 C.1 D.﹣1
10.随机掷一枚质地均匀的普通硬币两次,出现两次正面都朝上的概率是( )
A. B. C. D.
11.如图,⊙O的直径AB为3,点B为OD的中点,则AC的长为( )
A.2 B. C. D.
12.如图1,在矩形ABCD中,动点P从点B出发,设点P运动的路程为x,△ABP的面积为y,函数的图象如图2所示,则△ABC的面积为( )
A.15 B.16 C.20 D.30
二、填空题(本大题满分12分,每小题3分)
13.因式分解:x2+4y2﹣4xy= .
14.分式方程=3的解是 .
15.如图,在△ABC中,DE∥AC,DE=2,则AC= .
16.将矩形ABCD纸片按如图所示方式折叠,M、N分别为AB、CD的中点,点B的对应点B'恰好落在MN上.若AB=10,则DN的长为 ,折痕AE长为 .
三、解答题(本大题满分72分
17.(12分)(1)计算:(﹣1)2023+18÷(﹣)﹣2﹣×;
(2)求不等式组的所有整数解.
18.(10分)王阿姨去买水果,3kg芒果和2kg香蕉应付40元,可她把两种水果的单价弄反了
19.(10分)某中学初一年级刚搬迁到离市区较远的新校区,学校为了了解学生周末回家方式,从乘车、步行、骑车三个方面随机对该年级部分学生周末回家方式进行了一次调查统计(图1和图2),请你根据图中提供的信息解答下列问题:
(1)该学校采取的调查方式是 (填写“普查”或“抽样调查”);
(2)本次一共调查了 名学生,图1条形统计图中m= ;
(3)估计全年级860名学生中步行的有 人;
(4)预计今年秋季该校初一年级招生将增加10%,到时乘车回家人数约增加 人.
20.(10分)如图,在坡顶A处的同一水平面上有一座古塔BC(BC⊥AC),数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处又测得该塔的塔顶B的仰角为76°.
(1)填空:∠ABC= 度,∠PBC= 度;
(2)求坡顶A到地面PQ的距离;
(3)求古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4)
21.(15分)如图,在矩形ABCD中,AB=5,点E是边CD上一动点(点E不与C、D重合),延长DC到点F,连接AF与BE交于点G,AF与BC交于点H,BF.
(1)求证:①△ABG≌△FEG;②AE∥BF;
(2)若AG=AB,求线段GH的长;
(3)点E在运动过程中,△FEG的面积大小是否发生改变?若改变,请说明理由,请求出△FEG的面积.
22.(15分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣4,0)和点B,与y轴交于点C(0,3).
(1)求该抛物线的表达式;
(2)设点P(m,n)是直线AC上方抛物线上一点,过点P作PG⊥x轴,PG与直线AC交于点H.
①连接AP、CP,求四边形AOCP的面积S与m的函数关系式,并求出S的最大值;
②连接OH,在①的条件下,试判断四边形PHOC的形状;
③是否存在点P,使得以P、H、C为顶点的三角形是等腰三角形?若存在,请求出所有满足条件的m的值,请说明理由.
2023年海南省临高县中考数学模拟试卷
参考答案与试题解析
一、选择题(本大题满分36分,每小题3分)在下列各题的四个备选答案中,有且只有一个是正确的。
1.在0,﹣2,1,这四个数中( )
A.0 B.1 C.﹣2 D.
【分析】根据正数大于负数,两个负数比较大小,绝对值大的负数反而小,可得答案.
【解答】解:∵﹣2<0<<1,
∴最小的数是﹣2,
故选:C.
【点评】本题考查了有理数大小比较,两个负数比较大小,绝对值大的负数反而小.
2.计算m2 m3的结果是( )
A.6m B.5m C.m6 D.m5
【分析】根据同底数幂的乘法法则计算即可.
【解答】解:原式=m2+3
=m6,
故选:D.
【点评】本题考查了同底数幂的乘法,掌握am an=am+n是解题的关键.
3.中国信息通信研究院发布预测称,2025年中国5G用户规模将超过858000000人.将数据858000000用科学记数法表示为( )
A.8.58×1010 B.8.58×109 C.8.58×108 D.8.58×107
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数,当原数绝对值<1时,n是负整数.
【解答】解:将数据858000000用科学记数法表示为8.58×108.
故选:C.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
4.如图是由5个大小相同的小正方体摆成的立体图形,它的主视图是( )
A. B.
C. D.
【分析】找到从正面看所得到的图形即可.
【解答】解:从物体正面看,左边2个正方形.
故选:A.
【点评】本题考查了简单组合体的三视图,主视图是从物体的正面看得到的视图,解答时学生易将三种视图混淆而错误的选其它选项.
5.要使分式有意义,则x应满足的条件是( )
A.x≠1 B.x≠1或x≠0 C.x≠0 D.x>1
【分析】根据分式的分母不为零分式有意义,可得答案.
【解答】解:由分式有意义,得
x﹣1≠8,
解得x≠1.
故选:A.
【点评】本题考查了分式有意义的条件,分母不等于零分式有意义.
6.如图,已知AB∥CD,∠1=115°,则∠C等于( )
A.40° B.45° C.50° D.65°
【分析】根据平行线的性质得出∠3=115°,再根据三角形外角性质求解即可.
【解答】解:如图,
∵AB∥CD,∠1=115°,
∴∠1=∠3=115°,
∵∠3=∠C+∠2,∠5=65°,
∴∠C=50°,
故选:C.
【点评】此题考查了平行线的性质及三角形外角性质,熟记“两直线平行,同位角相等”是解题的关键.
7.如图,AD是△ABC的中线,若AB=8,AC=6,则AD等于( )
A.4 B.5 C.6 D.7
【分析】首先根据勾股定理逆定理可得△ABC是直角三角形,再根据直角三角形的性质:在直角三角形中,斜边上的中线等于斜边的一半可得AD=BC=5.
【解答】解:∵62+82=102,
∴△ABC是直角三角形,
∵AD是△ABC的中线,
∴AD=BC=5,
故选:B.
【点评】此题主要考查了直角三角形的性质以及勾股定理逆定理,关键是掌握在直角三角形中,斜边上的中线等于斜边的一半.
8.如图,在菱形ABCD中,AC=8,则△ABD的周长等于( )
A.20 B.18 C.16 D.14
【分析】根据菱形对角线互相垂直平分的性质,可以求得BO=OD,AO=OC,在Rt△AOD中,根据勾股定理可以求得AB的长,进而△ABD的周长.
【解答】解:菱形对角线互相垂直平分,
∴BO=OD=3,AO=OC=4,
∴AB=3,
∴△ABD的周长等于5+5+5=16,
故选:C.
【点评】本题考查了菱形面积的计算,考查了勾股定理在直角三角形中的运用,考查了菱形各边长相等的性质,本题中根据勾股定理计算AB的长是解题的关键.
9.已知点A(a,4)在双曲线上,则a的值是( )
A.4 B.﹣4 C.1 D.﹣1
【分析】把点A(a,4)代入即可得到结论.
【解答】解:∵点A(a,4)在双曲线上,
∴3=﹣,
∴a=﹣1,
故选:D.
【点评】本题考查了反比例函数的性质,反比例函数图形上点的坐标特征,熟练掌握反比例函数的性质是解题的关键.
10.随机掷一枚质地均匀的普通硬币两次,出现两次正面都朝上的概率是( )
A. B. C. D.
【分析】依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率即可解答.
【解答】解:画树状图如下:
共有4种等可能的结果,两次正面都朝上的情况有1种.
故选:B.
【点评】本题考查的是用列表法或画树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;用到的知识点为:概率=所求情况数与总情况数之比.
11.如图,⊙O的直径AB为3,点B为OD的中点,则AC的长为( )
A.2 B. C. D.
【分析】根据切线的性质可得∠OCD=90°,再根据线段的中点定义可得OD=2OB,从而可得OD=AB=3,然后在Rt△DOC中,利用锐角三角函数的定义可得sinD=,从而可得∠D=30°,进而利用直角三角形的边角关系可得OC=,DC=,∠DOC=60°,最后利用圆周角定理可得∠A=30°,从而可得∠D=∠A=30°,从而利用等角对等边可得DC=AC=,即可解答.
【解答】解:∵DC切⊙O于点C,
∴∠OCD=90°,
∵点B为OD的中点,
∴OD=2OB,
∵AB=2OB,
∴OD=AB=7,
在Rt△DOC中,OD=2OC=3,
∴sinD==,
∴∠D=30°,
∴OC=OD=OC=,
∴∠A=∠DOC=30°,
∴∠D=∠A=30°,
∴DC=AC=,
故选:D.
【点评】本题考查了切线的性质,圆周角定理,解直角三角形,熟练掌握切线的性质,以及圆周角定理是解题的关键.
12.如图1,在矩形ABCD中,动点P从点B出发,设点P运动的路程为x,△ABP的面积为y,函数的图象如图2所示,则△ABC的面积为( )
A.15 B.16 C.20 D.30
【分析】解本题需注意一定的面积值相对应的距离可以有2个.找到对应的点,找出准确反映y与x之间对应关系的图象,需分析在不同阶段中y随x变化的情况.
【解答】解:由图2知:
当动点P由B→C时,点P运动的路程为5,
∴BC=2,
当x=5和x=11时,△ABP的面积相等,
∴CD=6,
∴S△ABC=CD×BC=15,
故选:A.
【点评】解决本题的关键是读懂图意,得到相应的矩形中各边之间的关系.此题考查了学生从图象中读取信息的数形结合能力.
二、填空题(本大题满分12分,每小题3分)
13.因式分解:x2+4y2﹣4xy= (x﹣2y)2 .
【分析】直接利用完全平方公式进行分解即可.
【解答】解:原式=x2﹣4xy+4y2=(x﹣2y)5,
故答案为:(x﹣2y)2.
【点评】此题主要考查了公式法分解因式,关键是掌握完全平方公式:a2±2ab+b2=(a±b)2.
14.分式方程=3的解是 x=3 .
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
【解答】解:去分母得:2x=3x﹣4,
解得:x=3,
经检验x=3是分式方程的解.
故答案为:x=4
【点评】此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.
15.如图,在△ABC中,DE∥AC,DE=2,则AC= 5 .
【分析】根据相似三角形的判定和性质即可求得答案.
【解答】解:∵=,
∴=,
∵DE∥AC,
∴△BDE∽△BAC,
∴=,
∴=,
∴AC=5.
故答案为:7.
【点评】本题主要考查了相似三角形的判定和性质,熟知相似三角形的判定和性质是解决问题的关键.
16.将矩形ABCD纸片按如图所示方式折叠,M、N分别为AB、CD的中点,点B的对应点B'恰好落在MN上.若AB=10,则DN的长为 5 ,折痕AE长为 .
【分析】连接BB′,由AE垂直平分BB′,得AB′=AB,由矩形的性质得CD∥AB,CD=AB=10,∠ABC=90°,因为M、N分别为AB、CD的中点,所以AM∥DN,AM=DN=5,可证明四边形AMND是矩形,MN垂直平分AB,则BB′=AB′=AB,所以∠BAB′=60°,∠BAE=∠B′AE=∠BAB′=30°,则BE=AE,所以AB==AE=10,则AE=,于是得到问题的答案.
【解答】解:连接BB′,
由折叠得,点B′与点B关于直线AE对称,
∴AE垂直平分BB′,
∴AB′=AB,
∵四边形ABCD是矩形,AB=10,
∴CD∥AB,CD=AB=10,
∵M、N分别为AB,
∴AM∥DN,AM=DN=5,
∴四边形AMND是平行四边形,
∵∠D=90°,
∴四边形AMND是矩形,
∴∠AMN=90°,
∴MN垂直平分AB,
∴BB′=AB′=AB,
∴∠BAB′=60°,
∴∠BAE=∠B′AE=∠BAB′=30°,
∴BE=AE,
∴AB===AE,
∴AE=10,
解得AE=,
故答案为:2,.
【点评】此题重点考查矩形的判定与性质、轴对称的性质、线段的垂直平分线的性质、等边三角形的判定与性质、直角三角形中30°角所对的直角边等于斜边的一半等知识,证明BB′=AB′=AB是解题的关键.
三、解答题(本大题满分72分
17.(12分)(1)计算:(﹣1)2023+18÷(﹣)﹣2﹣×;
(2)求不等式组的所有整数解.
【分析】(1)原式利用乘方的意义,负整数指数幂法则,二次根式的乘法法则计算即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分确定出不等式组的解集,即可求出所有整数解.
【解答】解:(1)原式=﹣1+18÷9﹣
=﹣6+2﹣3
=﹣3;
(2),
解不等式①,得x<2;
解不等式②,得 ;
该不等式组的解集是:,
所以,该不等式组所有整数解为:﹣2,0,5.
【点评】此题考查了实数的运算,解一元一次不等式组,熟练掌握不等式组的解法是解本题的关键.
18.(10分)王阿姨去买水果,3kg芒果和2kg香蕉应付40元,可她把两种水果的单价弄反了
【分析】设王阿姨买的芒果的单价为x元/kg,香蕉的单价为y元/kg,根据“3kg芒果和2kg香蕉应付40元,2kg芒果和3kg香蕉应付35元”,可列出关于x,y的二元一次方程组,解之即可得出结论.
【解答】解:设王阿姨买的芒果的单价为x元/kg,香蕉的单价为y元/kg,
根据题意得:,
解得:.
答:王阿姨买的芒果的单价为10元/kg,香蕉的单价为5元/kg.
【点评】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
19.(10分)某中学初一年级刚搬迁到离市区较远的新校区,学校为了了解学生周末回家方式,从乘车、步行、骑车三个方面随机对该年级部分学生周末回家方式进行了一次调查统计(图1和图2),请你根据图中提供的信息解答下列问题:
(1)该学校采取的调查方式是 抽样调查 (填写“普查”或“抽样调查”);
(2)本次一共调查了 60 名学生,图1条形统计图中m= 12 ;
(3)估计全年级860名学生中步行的有 172 人;
(4)预计今年秋季该校初一年级招生将增加10%,到时乘车回家人数约增加 43 人.
【分析】(1)根据普查和抽样调查的定义解答即可;
(2)用“骑车”的人数除以30%可得样本容量,再用样本容量分别减去其他两种方式的人数可得m的值;
(3)用全年级人数乘样本值“步行”所占比例即可;
(4)根据题意列式计算即可得到结论.
【解答】解:(1)该学校采取的调查方式是抽样调查,
故答案为:抽样调查;
(2)本次一共调查了学生:18÷30%=60(名),
∴m=60﹣30﹣18=12.
故答案为:60,12;
(3)估计全年级860名学生中步行的有:860×=172(人),
故答案为:172;
(4)预计今年秋季该校初一年级招生将增加10%,到时乘车回家人数约增加:860×10%×,
故答案为:43.
【点评】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
20.(10分)如图,在坡顶A处的同一水平面上有一座古塔BC(BC⊥AC),数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处又测得该塔的塔顶B的仰角为76°.
(1)填空:∠ABC= 14 度,∠PBC= 45 度;
(2)求坡顶A到地面PQ的距离;
(3)求古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4)
【分析】(1)延长BC交PQ于点D,根据题意可得:∠BPD=45°,∠BAC=76°,BD⊥PQ,从而可得∠BDP=90°,然后利用直角三角形的两个锐角互余可得∠PBC=45°,再根据垂直定义可得∠BCA=90°,从而利用直角三角形的两个锐角互余可得∠ABC=14°,即可解答;
(2)过点A作AE⊥PQ,垂足为E,根据已知可设AE=5k米,则PE=12k米,然后在Rt△AEP中,利用勾股定理进行计算,即可解答;
(3)根据题意可得:CD=AE=10米,AC=DE,然后设AC=DE=y米,则DP=(y+24)米,然后在Rt△BDP中,利用锐角三角函数的定义求出BD的长,再在Rt△ABC中,利用锐角三角函数的定义求出BC的长,从而求出BD的长,最后列出关于y的方程,进行计算即可解答.
【解答】解:(1)延长BC交PQ于点D,
由题意得:∠BPD=45°,∠BAC=76°,
∴∠BDP=90°,
∴∠PBC=90°﹣∠BPD=45°,
∵BC⊥AC,
∴∠BCA=90°,
∴∠ABC=90°﹣∠BAC=14°,
故答案为:14;45;
(2)过点A作AE⊥PQ,垂足为E,
∵斜坡AP的坡度i=1:2.4,
∴==,
∴设AE=5k米,则PE=12k米,
在Rt△AEP中,AP==,
∵AP=26米,
∴13k=26,
解得:k=2,
∴AE=10米,PE=24米,
∴坡顶A到地面PQ的距离为10米;
(3)由题意得:CD=AE=10米,AC=DE,
设AC=DE=y米,
∵PE=24米,
∴PD=DE+PE=(y+24)米,
在Rt△BDP中,∠BPD=45°,
∴BD=PD tan45°=(y+24)米,
在Rt△ABC中,∠BAC=76°,
∴BC=AC tan76°≈2y(米),
∴BD=BC+CD=(4y+10)米,
∴y+24=4y+10,
解得:y=,
∴BC=4y≈19(米),
∴古塔BC的高度约为19米.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,坡度坡角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
21.(15分)如图,在矩形ABCD中,AB=5,点E是边CD上一动点(点E不与C、D重合),延长DC到点F,连接AF与BE交于点G,AF与BC交于点H,BF.
(1)求证:①△ABG≌△FEG;②AE∥BF;
(2)若AG=AB,求线段GH的长;
(3)点E在运动过程中,△FEG的面积大小是否发生改变?若改变,请说明理由,请求出△FEG的面积.
【分析】(1)①根据矩形的性质及全等三角形的判定即可证得.
②根据平行四边形的判定即可证得.
(2)根据矩形的性质和勾股定理求出DF,得到,求出HF,即可求解.
(3)过点G作GP⊥EF于点P,证明GP是△ADF 的中位线,求出GP,即可求解.
【解答】(1)证明:①∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,
∴∠BAG=∠EFG.
∵CF=DE,
∴CF+CE=DE+CE,
即EF=CD=AB.
又∵∠AGB=∠EGF,
∴△ABG≌△FEG(AAS).
②∵AB∥EF,AB=EF,
∴四边形ABEF是平行四边形,
∴AE∥BF.
(2)解:∵△ABG≌△FEG,
∴GF=AF=AB=5,
∴AF=10,
在矩形ABCD中,AD=BC=6,
在Rt△ADC中,DF=,
∴CF=DF﹣CD=4.
在矩形ABCD中,CH∥AD,
∴,
即,
解得,
∴GH=GF﹣HF=.
(3)解:△FEG的面积大小不变.
如图,过点G作GP⊥EF于点P,
则GP∥AD,
∵GF=AG,
∴DP=FP,
∴GP是△ADF 的中位线,
∴,
∴S△FEG=.
【点评】本题考查了四边形的综合应用,解题关键是掌握全等三角形的性质与判定,勾股定理,矩形的性质.
22.(15分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣4,0)和点B,与y轴交于点C(0,3).
(1)求该抛物线的表达式;
(2)设点P(m,n)是直线AC上方抛物线上一点,过点P作PG⊥x轴,PG与直线AC交于点H.
①连接AP、CP,求四边形AOCP的面积S与m的函数关系式,并求出S的最大值;
②连接OH,在①的条件下,试判断四边形PHOC的形状;
③是否存在点P,使得以P、H、C为顶点的三角形是等腰三角形?若存在,请求出所有满足条件的m的值,请说明理由.
【分析】(1)由待定系数法即可求解;
(2)①由S=S△AOC+S△AHP+S△CHP=,即可求解;
②由,即可求解;
③分HP=HC、CP=CH、PC=PH三种情况分别求解即可.
【解答】解:(1)由题意得:,
解得:,
则抛物线的表达式为:y=﹣;
(2)①∵A(﹣4,0),6),
设直线AC的表达式为:y=kx+3,
将点A的坐标代入上式得:0=﹣3k+3,
解得:k=,
∴直线AC的解析式为 ,
设点P的坐标为 ,故点H的坐标为 ,
则 .
∴四边形AOCP的面积S与m的函数关系式为:
S=S△AOC+S△AHP+S△CHP
=
=.
∵,﹣4<m<0,
∴当m=﹣8时,S有最大值;
②四边形PHOC是平行四边形,理由如下:
由①可得,当 m=﹣2 时,.
∵PH∥OC,
∴四边形PHOC是平行四边形;
③存在,理由如下:
∵点P的坐标为 ,点H的坐标为 ,
∴点G的坐标为(m,0),
则,OG=﹣m.
∵OA=4,OC=5,
∴AC=5.
∵PH∥OC,
,即
分三种情况讨论:
Ⅰ.当HP=HC时,
则 ,
解得:m=﹣或0 (舍去2).
Ⅱ.当 CP=CH 时,过点C作 CD⊥PH 于点D,
则 ,
∵DH+HG=DG=OC=8,
,
解得:m=﹣2或7 (0舍去).
Ⅲ.当 PC=PH 时,过点P作 PE⊥AC 于点E,
则
∠PEH=∠AGH=90°,∠PHE=∠AHG,
∴△PEH∽△AGH,
∴∠EPH=∠HAG,
∴sin∠EPH=sin∠HAG,
即 ,
,
解得:m=﹣或0 (舍去0),
综上所述,满足条件的m的值为 .
【点评】此题是二次函数的综合题,是中考的压轴题,难度较大,计算量也大,主要考查了待定系数法求解析式,还考查了三角形相似,平行四边形的性质等,分类求解是解决问题.
同课章节目录
