人教版八年级上册数学13.1.1 轴对称 同步测试(含答案)
文档属性
| 名称 | 人教版八年级上册数学13.1.1 轴对称 同步测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 280.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 21:18:46 | ||
图片预览


文档简介
人教版八年级上册数学13.1.1 轴对称 同步测试
一、单选题
1.在下列四个图案中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.下列表示天气符号的图形中,不是轴对称图形的是( )
A. B. C. D.
3.下面图形中,是轴对称图形的是( )
A. B. C. D.
4.下列图形中,是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
5.下列艺术字中,可以看作是轴对称图形的是( )
A. B. C. D.
6.下图均由正六边形与两条对角线所组成,其中不是轴对称图形的是( )
A. B. C. D.
7.窗棂即窗格(窗里面的横的或竖的格)是中国传统木构建筑的框架结构设计,窗棂上雕刻有线槽和各种花纹,构成种类繁多的优美图案,下列表示我国古代窗棂样式结构图案中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
8.下列四个图案中,不是轴对称图形的是( )
A. B. C. D.
9.下列图形中,不是轴对称图形的是( )
A. B. C. D.
10.剪纸是中国最古老的民间艺术之一,其在视觉上给人以透空的感觉和艺术享受.下列剪纸作品中,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
二、填空题
11.给出以下4个图形:①等边三角形,②平行四边形,③菱形,④正方形.其中既是轴对称图形又是中心对称图形的是 .(填写序号)
12.如图,在△ABC中,∠C=∠ABC=2∠A,BD是边AC上的高,则∠DBC的大小等于 度.
13.如图,已知直线 ,点 在直线 上,点 在直线 上,且 ,如果 的面积为3,那么 的面积等于 .
14.等边三角形有 条对称轴,矩形有 条对称轴.
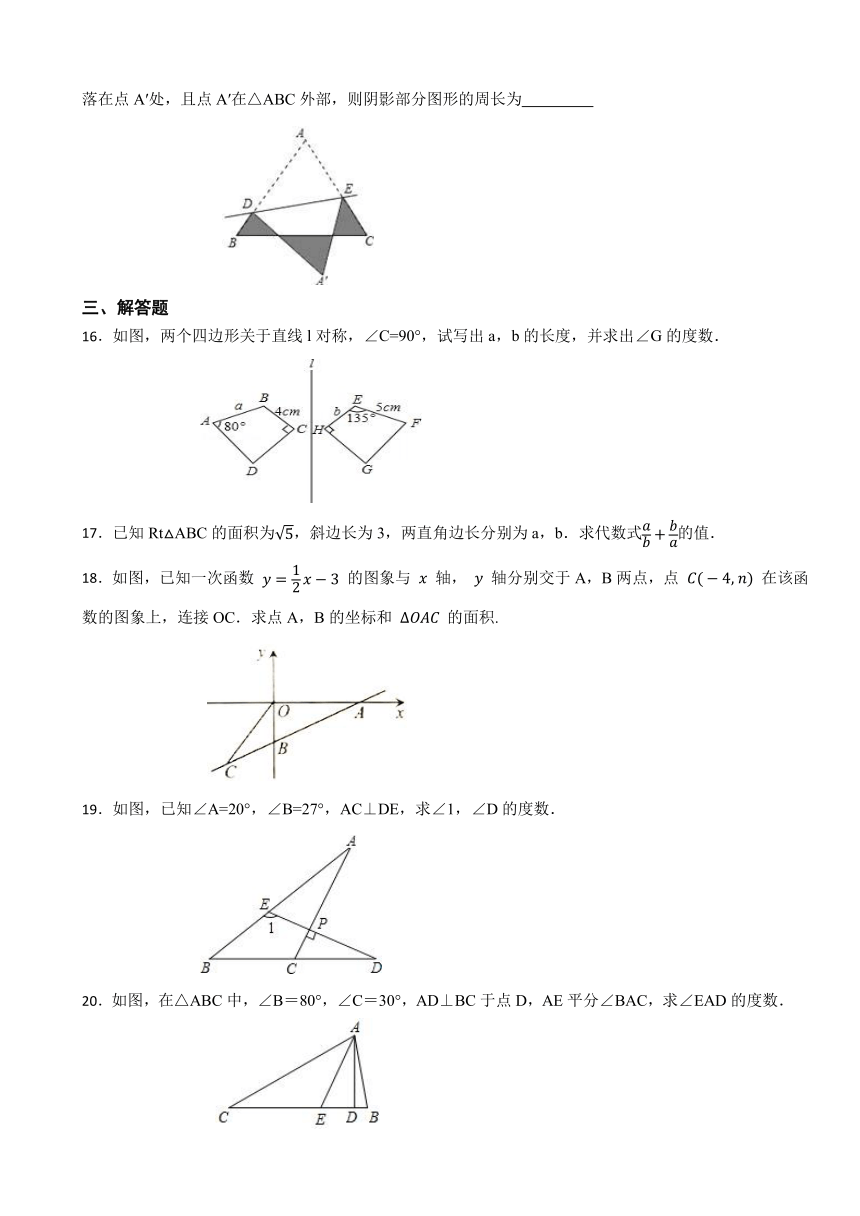
15.如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为
三、解答题
16.如图,两个四边形关于直线l对称,∠C=90°,试写出a,b的长度,并求出∠G的度数.
17.已知RtABC的面积为,斜边长为3,两直角边长分别为a,b.求代数式的值.
18.如图,已知一次函数 的图象与 轴, 轴分别交于A,B两点,点 在该函数的图象上,连接OC.求点A,B的坐标和 的面积.
19.如图,已知∠A=20°,∠B=27°,AC⊥DE,求∠1,∠D的度数.
20.如图,在△ABC中,∠B=80°,∠C=30°,AD⊥BC于点D,AE平分∠BAC,求∠EAD的度数.
21.如图,△ABC中,AD⊥BC,AE平分∠BAC,∠B=40°,∠C=60°,求∠DAE的度数.
22.如图,已知AB=DE,且AB∥DE,BE=CF.求证:△ABC≌△DEF.
23.如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=10,试求△PMN的周长.
24.如图,∠A=90°,E为BC上一点,A点和E点关于BD对称,B点、C点关于DE对称,求∠ABC和∠C的度数.
答 案
1.B 2.C 3.D 4.A 5.C 6.D 7.D 8.C 9.C 10.A 11.③④ 12.18
13.6 14.3;2 15.3.
16.解:∵两个四边形关于直线l对称,
∴四边形ABCD≌四边形FEHG,
∴∠H=∠C=90°,∠A=∠F=80°,∠E=∠B=135°,
∴∠G=360°﹣∠H﹣∠A﹣∠F=55°,
∴a=5cm b=4cm.
17.解:∵Rt△ABC的面积为,
∴ab=,
解得ab=2,
根据勾股定理得:a2+b2=32=9,
∴.
18.解:在 中,当 时, ,
点A的坐标为 ,
当 时, , 点B的坐标为
把点 代入 得
点C的坐标为
过点C作 轴于点D,则
19.解:∵AC⊥DE∴∠APE=90°又∵∠1是△APE的一个外角∴∠1=∠A+∠APE=20°+90°=110°在△BED中,∠1+∠B+∠D=180°∴∠D=180°-∠1-∠B=180°-110°-27°=43°.
20.∵∠B=80°,∠C=30°,
∴∠CAB=180°-80°-30°=70°,
∵AE平分∠BAC,
∴∠BAE= ∠BAC=35°,
∵AD⊥BC,
∴∠BAD=90°-∠B=10°,
∴∠EAD=∠BAE-∠BAD=25°.
21.解:∵∠B=40°,∠C=60°,
∴∠BAC=180°-∠B-∠C=80°,
∵AE平分∠BAC,
∴∠BAE= ∠BAC=40°,
∴∠AEC=∠B+∠BAE=80°,
∵AD⊥BC,
∴∠ADE=90°,
∴∠DAE=180°-∠ADE-∠AED=10°.
答:∠DAE的度数是10°.
22.证明:∵AB∥DE,∴∠B=∠DEF又∵BE=CF,∴BE+CE=CF+CE,即BC=EF,在△ABC与△DEF中,AB=DE,∠B=∠DEF,BC=EF,∴△ABC≌△DEF(SAS)
23.【解答】:∵P点关于OA、OB的对称点P1,P2,∴PM=P1M,PN=P2N,∴△PMN的周长=PM+MN+PN,=P1M+MN+P2N,=P1P2,∵P1P2=10,∴△PMN的周长=10.
24.解:∵A点和E点关于BD对称,
∴∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD.
又B点、C点关于DE对称,
∴∠DBE=∠C,∠ABC=2∠C.
∵∠A=90°,
∴∠ABC+∠C=2∠C+∠C=3∠C=90°.
∴∠C=30°,
∴∠ABC=2∠C=60°
一、单选题
1.在下列四个图案中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.下列表示天气符号的图形中,不是轴对称图形的是( )
A. B. C. D.
3.下面图形中,是轴对称图形的是( )
A. B. C. D.
4.下列图形中,是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
5.下列艺术字中,可以看作是轴对称图形的是( )
A. B. C. D.
6.下图均由正六边形与两条对角线所组成,其中不是轴对称图形的是( )
A. B. C. D.
7.窗棂即窗格(窗里面的横的或竖的格)是中国传统木构建筑的框架结构设计,窗棂上雕刻有线槽和各种花纹,构成种类繁多的优美图案,下列表示我国古代窗棂样式结构图案中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
8.下列四个图案中,不是轴对称图形的是( )
A. B. C. D.
9.下列图形中,不是轴对称图形的是( )
A. B. C. D.
10.剪纸是中国最古老的民间艺术之一,其在视觉上给人以透空的感觉和艺术享受.下列剪纸作品中,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
二、填空题
11.给出以下4个图形:①等边三角形,②平行四边形,③菱形,④正方形.其中既是轴对称图形又是中心对称图形的是 .(填写序号)
12.如图,在△ABC中,∠C=∠ABC=2∠A,BD是边AC上的高,则∠DBC的大小等于 度.
13.如图,已知直线 ,点 在直线 上,点 在直线 上,且 ,如果 的面积为3,那么 的面积等于 .
14.等边三角形有 条对称轴,矩形有 条对称轴.
15.如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为
三、解答题
16.如图,两个四边形关于直线l对称,∠C=90°,试写出a,b的长度,并求出∠G的度数.
17.已知RtABC的面积为,斜边长为3,两直角边长分别为a,b.求代数式的值.
18.如图,已知一次函数 的图象与 轴, 轴分别交于A,B两点,点 在该函数的图象上,连接OC.求点A,B的坐标和 的面积.
19.如图,已知∠A=20°,∠B=27°,AC⊥DE,求∠1,∠D的度数.
20.如图,在△ABC中,∠B=80°,∠C=30°,AD⊥BC于点D,AE平分∠BAC,求∠EAD的度数.
21.如图,△ABC中,AD⊥BC,AE平分∠BAC,∠B=40°,∠C=60°,求∠DAE的度数.
22.如图,已知AB=DE,且AB∥DE,BE=CF.求证:△ABC≌△DEF.
23.如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=10,试求△PMN的周长.
24.如图,∠A=90°,E为BC上一点,A点和E点关于BD对称,B点、C点关于DE对称,求∠ABC和∠C的度数.
答 案
1.B 2.C 3.D 4.A 5.C 6.D 7.D 8.C 9.C 10.A 11.③④ 12.18
13.6 14.3;2 15.3.
16.解:∵两个四边形关于直线l对称,
∴四边形ABCD≌四边形FEHG,
∴∠H=∠C=90°,∠A=∠F=80°,∠E=∠B=135°,
∴∠G=360°﹣∠H﹣∠A﹣∠F=55°,
∴a=5cm b=4cm.
17.解:∵Rt△ABC的面积为,
∴ab=,
解得ab=2,
根据勾股定理得:a2+b2=32=9,
∴.
18.解:在 中,当 时, ,
点A的坐标为 ,
当 时, , 点B的坐标为
把点 代入 得
点C的坐标为
过点C作 轴于点D,则
19.解:∵AC⊥DE∴∠APE=90°又∵∠1是△APE的一个外角∴∠1=∠A+∠APE=20°+90°=110°在△BED中,∠1+∠B+∠D=180°∴∠D=180°-∠1-∠B=180°-110°-27°=43°.
20.∵∠B=80°,∠C=30°,
∴∠CAB=180°-80°-30°=70°,
∵AE平分∠BAC,
∴∠BAE= ∠BAC=35°,
∵AD⊥BC,
∴∠BAD=90°-∠B=10°,
∴∠EAD=∠BAE-∠BAD=25°.
21.解:∵∠B=40°,∠C=60°,
∴∠BAC=180°-∠B-∠C=80°,
∵AE平分∠BAC,
∴∠BAE= ∠BAC=40°,
∴∠AEC=∠B+∠BAE=80°,
∵AD⊥BC,
∴∠ADE=90°,
∴∠DAE=180°-∠ADE-∠AED=10°.
答:∠DAE的度数是10°.
22.证明:∵AB∥DE,∴∠B=∠DEF又∵BE=CF,∴BE+CE=CF+CE,即BC=EF,在△ABC与△DEF中,AB=DE,∠B=∠DEF,BC=EF,∴△ABC≌△DEF(SAS)
23.【解答】:∵P点关于OA、OB的对称点P1,P2,∴PM=P1M,PN=P2N,∴△PMN的周长=PM+MN+PN,=P1M+MN+P2N,=P1P2,∵P1P2=10,∴△PMN的周长=10.
24.解:∵A点和E点关于BD对称,
∴∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD.
又B点、C点关于DE对称,
∴∠DBE=∠C,∠ABC=2∠C.
∵∠A=90°,
∴∠ABC+∠C=2∠C+∠C=3∠C=90°.
∴∠C=30°,
∴∠ABC=2∠C=60°
