2022-2023学年黑龙江省绥化市望奎县七年级(下)期末数学试卷(五四学制)(含解析)
文档属性
| 名称 | 2022-2023学年黑龙江省绥化市望奎县七年级(下)期末数学试卷(五四学制)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 314.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 22:07:38 | ||
图片预览



文档简介
2022-2023学年黑龙江省绥化市望奎县七年级(下)期末数学试卷(五四学制)
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1. 在,,,这四个实数中,最大的数是( )
A. B. C. D.
2. 如图,如果,那么,其依据可以简单说成( )
A. 两直线平行,内错角相等
B. 内错角相等,两直线平行
C. 两直线平行,同位角相等
D. 同位角相等,两直线平行
3. 在“互联网”时代,国家积极推动信息化技术与传统教学方式的深度融合,实现“线上线下”融合式教学模式变革为了了解某校七年级名学生对融合式教学模式的喜爱程度,从中抽取了名学生进行问卷调查以下说法错误的是( )
A. 样本容量是 B. 每个学生的喜爱程度是个体
C. 名学生的喜爱程度是总体 D. 名学生的喜爱程度是总体的一个样本
4. 已知点在轴的负半轴上,则点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
5. 化简:( )
A. B. C. D.
6. 如果,那么,的关系是( )
A. B. C. D. 无法确定
7. 已知是的解,则的值为( )
A. B. C. D.
8. 如图,将面积为的三角形沿方向平移至三角形的位置,平移的距离是边的倍,则图中的四边形的面积为( )
A.
B.
C.
D.
9. 关于的不等式组有四个整数解,则的取值范围是( )
A. B. C. D.
10. 盲盒近来火爆,这种不确定的“盲抽”模式受到了大家的喜爱,一服装厂用某种布料生产玩偶与玩偶组合成一批盲盒,一个盲盒搭配个玩偶和个玩偶,已知每米布料可做个玩偶或个玩偶,现计划用米这种布料生产这批盲盒不考虑面料的损耗,设用米布料做玩偶,用米布料做玩偶,使得恰好配套,则下列方程组正确的是( )
A. B. C. D.
二、填空题(本大题共10小题,共30.0分)
11. 在,,,,,中,无理数的个数为______ 个
12. 若,都是实数,且,则的立方根为______.
13. 在平面直角坐标系中,将点向右平移个单位长度,得到点,则点的坐标是______ .
14. 使不等式成立的的值中,最大整数为______.
15. 下列命题:不相交的直线是平行线;同位角相等;如果两个实数的平方相等,那么这两个实数也相等;对顶角相等.其中真命题的序号是________.
16. 已知二元一次方程的一组解为,则______.
17. 如图,,点在上,平分,,,则的度数是______.
18. 某校从参加计算机测试的学生中抽取了名学生的成绩分进行分析,并将其分成了六段后绘制成如图所示的频数分布直方图其中段因故看不清,若分以上含分为及格,试根据图中信息来估计这次测试的及格率约为______ .
19. 在实数范围内定义运算“”:,例如:,如果,则的值是______ .
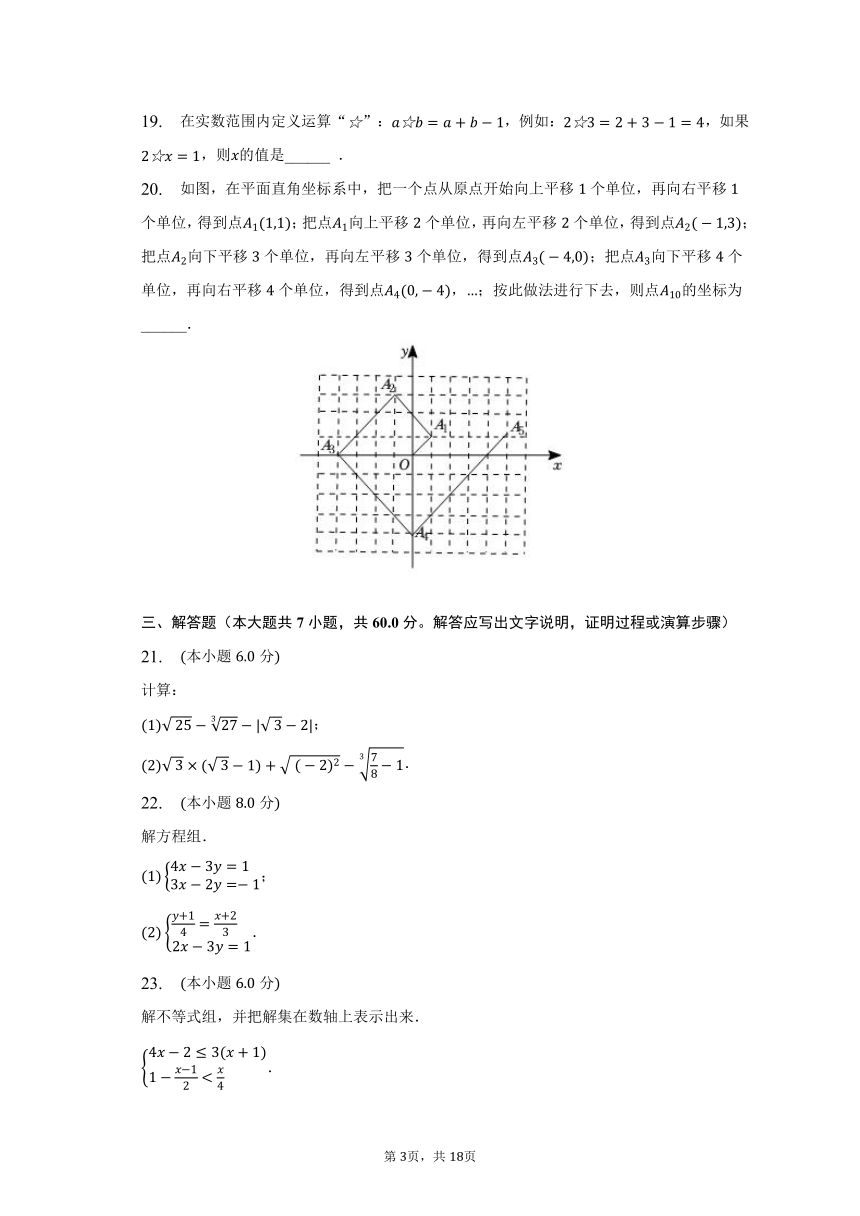
20. 如图,在平面直角坐标系中,把一个点从原点开始向上平移个单位,再向右平移个单位,得到点;把点向上平移个单位,再向左平移个单位,得到点;把点向下平移个单位,再向左平移个单位,得到点;把点向下平移个单位,再向右平移个单位,得到点,;按此做法进行下去,则点的坐标为______.
三、解答题(本大题共7小题,共60.0分。解答应写出文字说明,证明过程或演算步骤)
21. 本小题分
计算:
;
.
22. 本小题分
解方程组.
;
.
23. 本小题分
解不等式组,并把解集在数轴上表示出来.
.
24. 本小题分
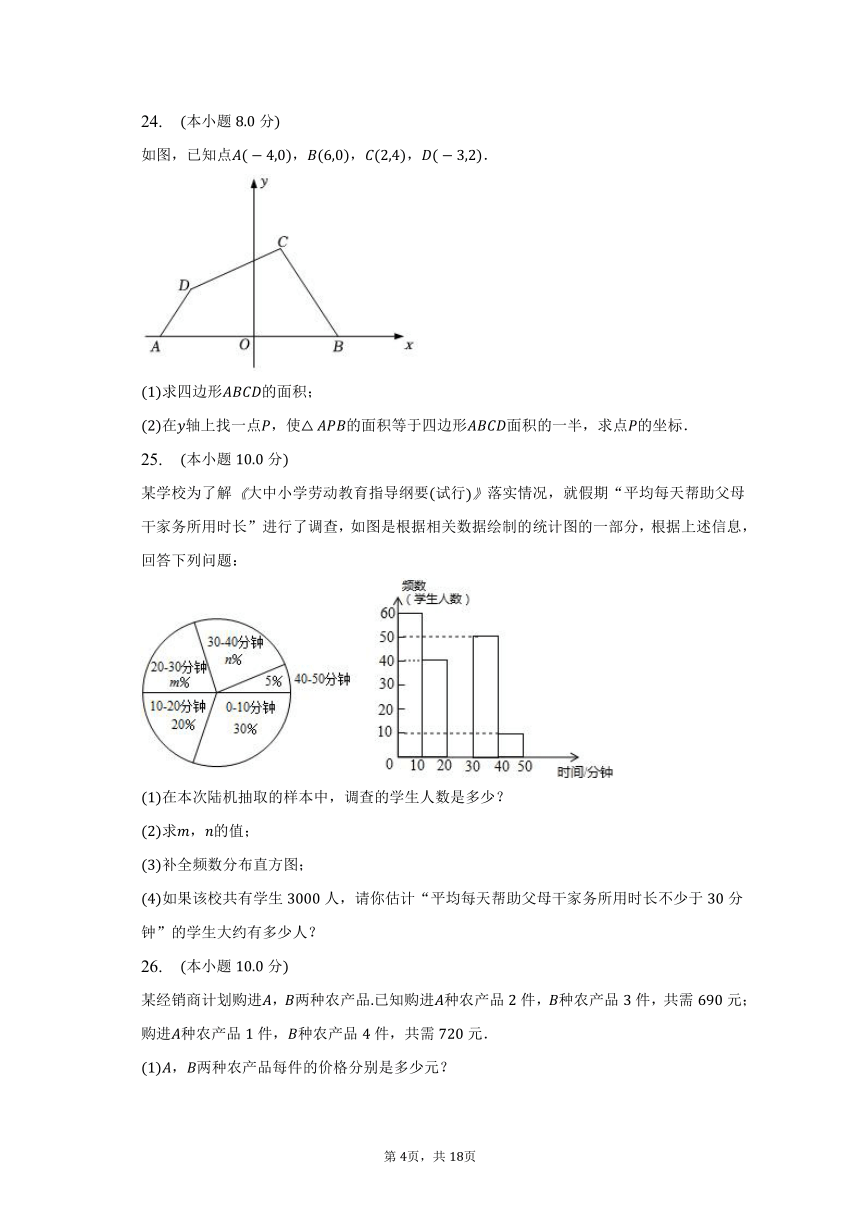
如图,已知点,,,.
求四边形的面积;
在轴上找一点,使的面积等于四边形面积的一半,求点的坐标.
25. 本小题分
某学校为了解大中小学劳动教育指导纲要试行落实情况,就假期“平均每天帮助父母干家务所用时长”进行了调查,如图是根据相关数据绘制的统计图的一部分,根据上述信息,回答下列问题:
在本次陆机抽取的样本中,调查的学生人数是多少?
求,的值;
补全频数分布直方图;
如果该校共有学生人,请你估计“平均每天帮助父母干家务所用时长不少于分钟”的学生大约有多少人?
26. 本小题分
某经销商计划购进,两种农产品已知购进种农产品件,种农产品件,共需元;购进种农产品件,种农产品件,共需元.
,两种农产品每件的价格分别是多少元?
该经销商计划用不超过元购进,两种农产品共件,且种农产品的件数不超过种农产品件数的倍,那么购进种农产品件数的范围是多少?
27. 本小题分
三角形中,是上一点,交于点,点是线段延长线上一点,连接,.
如图,求证:;
如图,连接,若,,求的度数;
如图,在的条件下,点是线段延长线上一点,若::,平分,求的度数.
答案和解析
1.【答案】
【解析】解:,
最大的数是;
故选:.
根据实数的大小比较法则即可得出答案.
此题考查了实数的大小比较,熟练掌握掌握大于,负数小于,正数大于一切负数.
2.【答案】
【解析】解:,
同位角相等,两直线平行,
故选:.
由平行线的判定求解.
本题考查平行线的判定,解题关键是掌握平行线的判定方法.
3.【答案】
【解析】解:为了了解某校七年级名学生对融合式教学模式的喜爱程度,从中抽取了名学生进行问卷调查,其样本容量是,故A正确,不符合题意;
每个学生的喜爱程度是个体,故B正确,不符合题意;
名学生的喜爱程度是总体的一个样本,故C错误,符合题意,D正确,不符合题意.
故选:.
根据总体、个体、样本、样本容量的定义进行解答即可.
本题主要考查了总体、个体、样本、样本容量的定义,熟练掌握总体:我们把所要考察的对象的全体叫做总体;个体:把组成总体的每一个考察对象叫做个体;样本:从总体中取出的一部分个体叫做这个总体的一个样本;样本容量:一个样本中所包含的数量,是解题的关键.
4.【答案】
【解析】解:由点在轴的负半轴上,得
.
所以,,
则点在第一象限,
故选:.
根据轴的负半轴上点的横坐标等于零,纵坐标小于零,即可解答.
本题考查了点的坐标,熟悉各象限内点坐标的符号是解题关键.
5.【答案】
【解析】解:.
故选:.
利用二次根式的性质进行化简,即可得到答案.
本题考查了二次根式的性质,熟练掌握是解题关键.
6.【答案】
【解析】解:,
,
故选:.
由立方根的性质,可知时,.
本题考查立方根;熟练掌握立方根的性质是解题的关键.
7.【答案】
【解析】解:把代入方程组得:,
解得:,
,
故选:.
把代入方程组得出,求出方程组的解,再求出的值即可.
本题考查了二元一次方程的解和解二元一次方程组,能求出、的值是解此题的关键.
8.【答案】
【解析】解:连接,如图,
三角形沿方向平移至三角形的位置,平移的距离是边长的两倍,
,,,,
,
,
点和点到的距离相等,
,
,
,
,
,
四边形的面积为.
故选:.
连接,如图,根据平移的性质得到,,,,则,根据平行线的性质得到点和点到的距离相等,则利用三角形面积公式得到,且,从而得到.
本题考查了三角形的面积:三角形的面积等于底边长与高线乘积的一半,即底高.也考查了平移的性质.
9.【答案】
【解析】解:
由得;
由得;
关于的不等式组有四个整数解,
其解集为,
且四个整数解为,,,,
则,
解得.
故选:.
本题考查不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.
先求出不等式组中每个不等式的解集,然后求出其公共解集,最后求的取值范围即可.
10.【答案】
【解析】解:现计划用米这种布料生产这批盲盒,用米布料做玩偶,用米布料做玩偶,
;
每米布料可做个玩偶或个玩偶,一个盲盒搭配个玩偶和个玩偶,且生产的两种玩偶恰好配套,
.
根据题意可列出方程组.
故选:.
根据生产玩偶的布料的总长度及生产的玩偶的总数量是生产的玩偶总数量的倍,即可得出关于,的二元一次方程组,此题得解.
本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
11.【答案】
【解析】解:,
所以在,,,,,中,无理数有,,,共个.
故答案为:.
根据无理数是无限不循环小数,可得无理数.
本题主要考查了无理数,注意带根号的数不一定是无理数,无理数是无限不循环小数.
12.【答案】
【解析】解:根据题意得,且,
解得且,
所以,,
,
,
,
的立方根为.
故答案为:.
根据被开方数大于等于列式求出的值,然后求出的值,代入代数式求解,再根据立方根的定义解答.
本题考查的知识点为:二次根式的被开方数是非负数,立方根的定义,根据的取值范围求出的值是解题的关键.
13.【答案】
【解析】解:点向右平移个单位长度后得到点的坐标为,即,
故答案为:.
利用“横坐标,右移加,左移减;纵坐标,上移加,下移减”的规律求解可得.
此题主要考查了坐标与图形的变化平移,关键是掌握横坐标,右移加,左移减;纵坐标,上移加,下移减.
14.【答案】:
【解析】解:移项、合并同类项,得;
系数化为,得;
使不等式成立的值中的最大整数是.
故答案为:.
先求出不等式的解集,然后求其最大整数解.
本题考查了一元一次不等式的整数解,正确解不等式,求出解集是解答本题的关键.
15.【答案】
【解析】解:在同一平面内,不相交的直线是平行线,所以错误;
两直线平行,同位角相等,所以错误;
如果两个实数的平方相等,那么这两个实数相等或互为相反数,所以错误;
对顶角相等,所以正确.
故答案为.
根据同一平面内两直线的位置关系对进行判断;根据平行线的性质对进行判断;根据平方根的定义对进行判断;根据对顶角的性质对进行判断.
本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果那么”形式.、有些命题的正确性是用推理证实的,这样的真命题叫做定理.
16.【答案】
【解析】解:二元一次方程的一组解为,
,
,
,
故答案为:
把,代入方程,得出,求出,再代入求出答案即可.
本题考查了二二元一次方程的解和求代数式的值,能求出是解此题的关键,用了整体代入思想.
17.【答案】
【解析】解:,,
,,
,
平分,
,
,
,
,
.
故答案为:.
根据平行线的性质解答即可.
此题考查平行线的性质,解题的关键是熟练掌握平行线的性质.
18.【答案】
【解析】解:第一组的频数是,
第二组的频数是,
则不及格的人数是人,及格人数是人,
则及格率是.
故答案是:.
利用每一组对应的纵坐标的数值乘以组距,即可求得每组的频数,求得不及格的频数,则及格人数即可求得,从而求得及格率.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
19.【答案】
【解析】解:,
,
解得:.
故答案为:.
直接利用已知运算公式得出关于的一元一次方程,进而得出答案.
此题主要考查了实数的运算以及解一元一次方程,正确运用运算规律将原式变形是解题关键.
20.【答案】
【解析】解:由图象可知,,
将点向左平移个单位、再向上平移个单位,可得,
将点向左平移个单位,再向下平移个单位,可得,
将点向右平移个单位,再向下平移个单位,可得,
将点向右平移个单位,再向上平移个单位,可得,
将点向左平移平移个单位,再向上平移个单位,可得,
故答案为:.
根据题目规律,依次求出、的坐标即可.
本题主要考查了坐标与图形变化平移,规律型问题,解题的关键是学会探究规律,属于中考常考题型.
21.【答案】解:原式
;
原式
.
【解析】利用算术平方根的定义,立方根的定义,绝对值的性质进行计算即可;
利用二次根式的乘法法则,算术平方根的定义,立方根的定义进行计算即可.
本题考查实数的运算,熟练掌握相关运算法则是解题的关键.
22.【答案】解:,
得:,
得:,
得:,
解得:,
把代入得:,
解得:,
故方程组的解是:;
,
整理得:,
得:,
解得:,
把代入得:,
解得:,
故原方程组的解是:.
【解析】利用加减消元法进行求解即可;
利用加减消元法进行求解即可.
本题主要考查解二元一次方程组,解答的关键是熟练掌握解二元一次方程组的方法.
23.【答案】解:,
解不等式得:,
解不等式得:,
在同一条数轴上表示不等式的解集,如图所示,
原不等式组的解集为.
【解析】根据解一元一次不等式组的一般步骤,进行计算即可.
本题考查了解一元一次不等式组,掌握解一元一次不等式组的一般步骤是解决问题的关键.
24.【答案】解:分别过、两点作轴的垂线,垂足分别为、,
则.
设的边上高为,
由,得
,
解得.
又点在轴上,
或.
【解析】观察图形,用分割法求解,分别过、两点作轴的垂线,将图形分割为两个直角三角形和一个直角梯形,再根据直角三角形和直角梯形的面积公式求面积和即可;
点纵坐标到原点的距离就是的边上的高,根据点到原点的距离,再根据点分别在轴正负半轴,写出点的坐标即可.
本题考查多边形面积及坐标系的基础知识,熟练掌握基础图形的面积公式是关键.
25.【答案】解:在本次随机抽取的样本中,调查的学生人数是人;
分钟的人数为人,
,,
、;
补全频数分布直方图如下:
人.
答:该校共有学生人,估计“平均每天帮助父母干家务所用时长不少于分钟”的学生大约有人.
【解析】本题考查频数分布直方图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
由分钟的人数及其所占百分比可得总人数;
先根据个分组的人数之和等于总人数求出的人数,再分别用、分钟的人数除以被调查的总人数即可求出、的值;
根据以上所求结果即可补全图形;
用总人数乘以样本中、分钟人数和占被调查人数的比例即可.
26.【答案】解:设种农产品每件的价格是元,种农产品每件的价格是元,
依题意得:,
解得:,
答:种农产品每件的价格是元,种农产品每件的价格是元;
设该经销商购进种农产品件,则购进种农产品件,
依题意得:,
解得:,
答:购进种农产品件数的范围是.
【解析】设种农产品的每件价格是元,种农产品每件的价格是元,根据“购进种农产品件,种农产品件,共需元;购进种农产品件,种农产品件,共需元”,列出二元一次方程组,解之即可得出结论;
设该经销商购进种农产品件,则购进种农产品件,利用总价单价数量,结合购进种农产品的件数不超过种农产品件数的倍且总价不超过元,列出一元一次不等式组,解之即可得出的取值范围.
本题考查了二元一次方程组的应用以及一元一次不等式组的应用,解题的关键是:找准等量关系,正确列出二元一次方程组;找出数量关系,正确列出一元一次不等式组.
27.【答案】证明:,
,
.
.
;
解:如图,过点作,
,
,
,
,
;
平分,
,
::,
设,则,
,
,,
,
,
解得,
,
,
.
【解析】根据平行线的判定与性质即可完成证明;
如图,过点作,可得,再根据平行线的性质即可得结论;
根据::,可以设,则,然后根据,,求出的值,进而可得结果.
本题考查了平行线的判定与性质,解决本题的关键是掌握平行线的判定与性质.
第1页,共1页
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1. 在,,,这四个实数中,最大的数是( )
A. B. C. D.
2. 如图,如果,那么,其依据可以简单说成( )
A. 两直线平行,内错角相等
B. 内错角相等,两直线平行
C. 两直线平行,同位角相等
D. 同位角相等,两直线平行
3. 在“互联网”时代,国家积极推动信息化技术与传统教学方式的深度融合,实现“线上线下”融合式教学模式变革为了了解某校七年级名学生对融合式教学模式的喜爱程度,从中抽取了名学生进行问卷调查以下说法错误的是( )
A. 样本容量是 B. 每个学生的喜爱程度是个体
C. 名学生的喜爱程度是总体 D. 名学生的喜爱程度是总体的一个样本
4. 已知点在轴的负半轴上,则点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
5. 化简:( )
A. B. C. D.
6. 如果,那么,的关系是( )
A. B. C. D. 无法确定
7. 已知是的解,则的值为( )
A. B. C. D.
8. 如图,将面积为的三角形沿方向平移至三角形的位置,平移的距离是边的倍,则图中的四边形的面积为( )
A.
B.
C.
D.
9. 关于的不等式组有四个整数解,则的取值范围是( )
A. B. C. D.
10. 盲盒近来火爆,这种不确定的“盲抽”模式受到了大家的喜爱,一服装厂用某种布料生产玩偶与玩偶组合成一批盲盒,一个盲盒搭配个玩偶和个玩偶,已知每米布料可做个玩偶或个玩偶,现计划用米这种布料生产这批盲盒不考虑面料的损耗,设用米布料做玩偶,用米布料做玩偶,使得恰好配套,则下列方程组正确的是( )
A. B. C. D.
二、填空题(本大题共10小题,共30.0分)
11. 在,,,,,中,无理数的个数为______ 个
12. 若,都是实数,且,则的立方根为______.
13. 在平面直角坐标系中,将点向右平移个单位长度,得到点,则点的坐标是______ .
14. 使不等式成立的的值中,最大整数为______.
15. 下列命题:不相交的直线是平行线;同位角相等;如果两个实数的平方相等,那么这两个实数也相等;对顶角相等.其中真命题的序号是________.
16. 已知二元一次方程的一组解为,则______.
17. 如图,,点在上,平分,,,则的度数是______.
18. 某校从参加计算机测试的学生中抽取了名学生的成绩分进行分析,并将其分成了六段后绘制成如图所示的频数分布直方图其中段因故看不清,若分以上含分为及格,试根据图中信息来估计这次测试的及格率约为______ .
19. 在实数范围内定义运算“”:,例如:,如果,则的值是______ .
20. 如图,在平面直角坐标系中,把一个点从原点开始向上平移个单位,再向右平移个单位,得到点;把点向上平移个单位,再向左平移个单位,得到点;把点向下平移个单位,再向左平移个单位,得到点;把点向下平移个单位,再向右平移个单位,得到点,;按此做法进行下去,则点的坐标为______.
三、解答题(本大题共7小题,共60.0分。解答应写出文字说明,证明过程或演算步骤)
21. 本小题分
计算:
;
.
22. 本小题分
解方程组.
;
.
23. 本小题分
解不等式组,并把解集在数轴上表示出来.
.
24. 本小题分
如图,已知点,,,.
求四边形的面积;
在轴上找一点,使的面积等于四边形面积的一半,求点的坐标.
25. 本小题分
某学校为了解大中小学劳动教育指导纲要试行落实情况,就假期“平均每天帮助父母干家务所用时长”进行了调查,如图是根据相关数据绘制的统计图的一部分,根据上述信息,回答下列问题:
在本次陆机抽取的样本中,调查的学生人数是多少?
求,的值;
补全频数分布直方图;
如果该校共有学生人,请你估计“平均每天帮助父母干家务所用时长不少于分钟”的学生大约有多少人?
26. 本小题分
某经销商计划购进,两种农产品已知购进种农产品件,种农产品件,共需元;购进种农产品件,种农产品件,共需元.
,两种农产品每件的价格分别是多少元?
该经销商计划用不超过元购进,两种农产品共件,且种农产品的件数不超过种农产品件数的倍,那么购进种农产品件数的范围是多少?
27. 本小题分
三角形中,是上一点,交于点,点是线段延长线上一点,连接,.
如图,求证:;
如图,连接,若,,求的度数;
如图,在的条件下,点是线段延长线上一点,若::,平分,求的度数.
答案和解析
1.【答案】
【解析】解:,
最大的数是;
故选:.
根据实数的大小比较法则即可得出答案.
此题考查了实数的大小比较,熟练掌握掌握大于,负数小于,正数大于一切负数.
2.【答案】
【解析】解:,
同位角相等,两直线平行,
故选:.
由平行线的判定求解.
本题考查平行线的判定,解题关键是掌握平行线的判定方法.
3.【答案】
【解析】解:为了了解某校七年级名学生对融合式教学模式的喜爱程度,从中抽取了名学生进行问卷调查,其样本容量是,故A正确,不符合题意;
每个学生的喜爱程度是个体,故B正确,不符合题意;
名学生的喜爱程度是总体的一个样本,故C错误,符合题意,D正确,不符合题意.
故选:.
根据总体、个体、样本、样本容量的定义进行解答即可.
本题主要考查了总体、个体、样本、样本容量的定义,熟练掌握总体:我们把所要考察的对象的全体叫做总体;个体:把组成总体的每一个考察对象叫做个体;样本:从总体中取出的一部分个体叫做这个总体的一个样本;样本容量:一个样本中所包含的数量,是解题的关键.
4.【答案】
【解析】解:由点在轴的负半轴上,得
.
所以,,
则点在第一象限,
故选:.
根据轴的负半轴上点的横坐标等于零,纵坐标小于零,即可解答.
本题考查了点的坐标,熟悉各象限内点坐标的符号是解题关键.
5.【答案】
【解析】解:.
故选:.
利用二次根式的性质进行化简,即可得到答案.
本题考查了二次根式的性质,熟练掌握是解题关键.
6.【答案】
【解析】解:,
,
故选:.
由立方根的性质,可知时,.
本题考查立方根;熟练掌握立方根的性质是解题的关键.
7.【答案】
【解析】解:把代入方程组得:,
解得:,
,
故选:.
把代入方程组得出,求出方程组的解,再求出的值即可.
本题考查了二元一次方程的解和解二元一次方程组,能求出、的值是解此题的关键.
8.【答案】
【解析】解:连接,如图,
三角形沿方向平移至三角形的位置,平移的距离是边长的两倍,
,,,,
,
,
点和点到的距离相等,
,
,
,
,
,
四边形的面积为.
故选:.
连接,如图,根据平移的性质得到,,,,则,根据平行线的性质得到点和点到的距离相等,则利用三角形面积公式得到,且,从而得到.
本题考查了三角形的面积:三角形的面积等于底边长与高线乘积的一半,即底高.也考查了平移的性质.
9.【答案】
【解析】解:
由得;
由得;
关于的不等式组有四个整数解,
其解集为,
且四个整数解为,,,,
则,
解得.
故选:.
本题考查不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.
先求出不等式组中每个不等式的解集,然后求出其公共解集,最后求的取值范围即可.
10.【答案】
【解析】解:现计划用米这种布料生产这批盲盒,用米布料做玩偶,用米布料做玩偶,
;
每米布料可做个玩偶或个玩偶,一个盲盒搭配个玩偶和个玩偶,且生产的两种玩偶恰好配套,
.
根据题意可列出方程组.
故选:.
根据生产玩偶的布料的总长度及生产的玩偶的总数量是生产的玩偶总数量的倍,即可得出关于,的二元一次方程组,此题得解.
本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
11.【答案】
【解析】解:,
所以在,,,,,中,无理数有,,,共个.
故答案为:.
根据无理数是无限不循环小数,可得无理数.
本题主要考查了无理数,注意带根号的数不一定是无理数,无理数是无限不循环小数.
12.【答案】
【解析】解:根据题意得,且,
解得且,
所以,,
,
,
,
的立方根为.
故答案为:.
根据被开方数大于等于列式求出的值,然后求出的值,代入代数式求解,再根据立方根的定义解答.
本题考查的知识点为:二次根式的被开方数是非负数,立方根的定义,根据的取值范围求出的值是解题的关键.
13.【答案】
【解析】解:点向右平移个单位长度后得到点的坐标为,即,
故答案为:.
利用“横坐标,右移加,左移减;纵坐标,上移加,下移减”的规律求解可得.
此题主要考查了坐标与图形的变化平移,关键是掌握横坐标,右移加,左移减;纵坐标,上移加,下移减.
14.【答案】:
【解析】解:移项、合并同类项,得;
系数化为,得;
使不等式成立的值中的最大整数是.
故答案为:.
先求出不等式的解集,然后求其最大整数解.
本题考查了一元一次不等式的整数解,正确解不等式,求出解集是解答本题的关键.
15.【答案】
【解析】解:在同一平面内,不相交的直线是平行线,所以错误;
两直线平行,同位角相等,所以错误;
如果两个实数的平方相等,那么这两个实数相等或互为相反数,所以错误;
对顶角相等,所以正确.
故答案为.
根据同一平面内两直线的位置关系对进行判断;根据平行线的性质对进行判断;根据平方根的定义对进行判断;根据对顶角的性质对进行判断.
本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果那么”形式.、有些命题的正确性是用推理证实的,这样的真命题叫做定理.
16.【答案】
【解析】解:二元一次方程的一组解为,
,
,
,
故答案为:
把,代入方程,得出,求出,再代入求出答案即可.
本题考查了二二元一次方程的解和求代数式的值,能求出是解此题的关键,用了整体代入思想.
17.【答案】
【解析】解:,,
,,
,
平分,
,
,
,
,
.
故答案为:.
根据平行线的性质解答即可.
此题考查平行线的性质,解题的关键是熟练掌握平行线的性质.
18.【答案】
【解析】解:第一组的频数是,
第二组的频数是,
则不及格的人数是人,及格人数是人,
则及格率是.
故答案是:.
利用每一组对应的纵坐标的数值乘以组距,即可求得每组的频数,求得不及格的频数,则及格人数即可求得,从而求得及格率.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
19.【答案】
【解析】解:,
,
解得:.
故答案为:.
直接利用已知运算公式得出关于的一元一次方程,进而得出答案.
此题主要考查了实数的运算以及解一元一次方程,正确运用运算规律将原式变形是解题关键.
20.【答案】
【解析】解:由图象可知,,
将点向左平移个单位、再向上平移个单位,可得,
将点向左平移个单位,再向下平移个单位,可得,
将点向右平移个单位,再向下平移个单位,可得,
将点向右平移个单位,再向上平移个单位,可得,
将点向左平移平移个单位,再向上平移个单位,可得,
故答案为:.
根据题目规律,依次求出、的坐标即可.
本题主要考查了坐标与图形变化平移,规律型问题,解题的关键是学会探究规律,属于中考常考题型.
21.【答案】解:原式
;
原式
.
【解析】利用算术平方根的定义,立方根的定义,绝对值的性质进行计算即可;
利用二次根式的乘法法则,算术平方根的定义,立方根的定义进行计算即可.
本题考查实数的运算,熟练掌握相关运算法则是解题的关键.
22.【答案】解:,
得:,
得:,
得:,
解得:,
把代入得:,
解得:,
故方程组的解是:;
,
整理得:,
得:,
解得:,
把代入得:,
解得:,
故原方程组的解是:.
【解析】利用加减消元法进行求解即可;
利用加减消元法进行求解即可.
本题主要考查解二元一次方程组,解答的关键是熟练掌握解二元一次方程组的方法.
23.【答案】解:,
解不等式得:,
解不等式得:,
在同一条数轴上表示不等式的解集,如图所示,
原不等式组的解集为.
【解析】根据解一元一次不等式组的一般步骤,进行计算即可.
本题考查了解一元一次不等式组,掌握解一元一次不等式组的一般步骤是解决问题的关键.
24.【答案】解:分别过、两点作轴的垂线,垂足分别为、,
则.
设的边上高为,
由,得
,
解得.
又点在轴上,
或.
【解析】观察图形,用分割法求解,分别过、两点作轴的垂线,将图形分割为两个直角三角形和一个直角梯形,再根据直角三角形和直角梯形的面积公式求面积和即可;
点纵坐标到原点的距离就是的边上的高,根据点到原点的距离,再根据点分别在轴正负半轴,写出点的坐标即可.
本题考查多边形面积及坐标系的基础知识,熟练掌握基础图形的面积公式是关键.
25.【答案】解:在本次随机抽取的样本中,调查的学生人数是人;
分钟的人数为人,
,,
、;
补全频数分布直方图如下:
人.
答:该校共有学生人,估计“平均每天帮助父母干家务所用时长不少于分钟”的学生大约有人.
【解析】本题考查频数分布直方图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
由分钟的人数及其所占百分比可得总人数;
先根据个分组的人数之和等于总人数求出的人数,再分别用、分钟的人数除以被调查的总人数即可求出、的值;
根据以上所求结果即可补全图形;
用总人数乘以样本中、分钟人数和占被调查人数的比例即可.
26.【答案】解:设种农产品每件的价格是元,种农产品每件的价格是元,
依题意得:,
解得:,
答:种农产品每件的价格是元,种农产品每件的价格是元;
设该经销商购进种农产品件,则购进种农产品件,
依题意得:,
解得:,
答:购进种农产品件数的范围是.
【解析】设种农产品的每件价格是元,种农产品每件的价格是元,根据“购进种农产品件,种农产品件,共需元;购进种农产品件,种农产品件,共需元”,列出二元一次方程组,解之即可得出结论;
设该经销商购进种农产品件,则购进种农产品件,利用总价单价数量,结合购进种农产品的件数不超过种农产品件数的倍且总价不超过元,列出一元一次不等式组,解之即可得出的取值范围.
本题考查了二元一次方程组的应用以及一元一次不等式组的应用,解题的关键是:找准等量关系,正确列出二元一次方程组;找出数量关系,正确列出一元一次不等式组.
27.【答案】证明:,
,
.
.
;
解:如图,过点作,
,
,
,
,
;
平分,
,
::,
设,则,
,
,,
,
,
解得,
,
,
.
【解析】根据平行线的判定与性质即可完成证明;
如图,过点作,可得,再根据平行线的性质即可得结论;
根据::,可以设,则,然后根据,,求出的值,进而可得结果.
本题考查了平行线的判定与性质,解决本题的关键是掌握平行线的判定与性质.
第1页,共1页
同课章节目录
