4.3.1等比数列的概念 课件(共18张PPT)
文档属性
| 名称 | 4.3.1等比数列的概念 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 721.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 17:56:27 | ||
图片预览






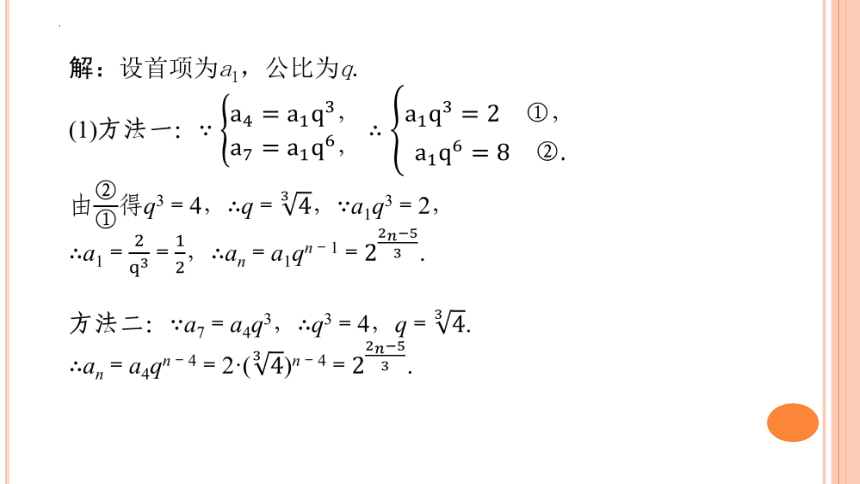
文档简介
(共18张PPT)
4.3.1等比数列的概念
一、等比数列的概念
(1)文字语言:一般地,如果一个数列从第_____项起,每一项与它的前一项的比都等于__________常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母________表示.
(2)符号语言:=q(q为常数,n∈N*)
注释:
1. 等比数列中不能出现0,公比不能为0;
2. 当q=1时,此时为常数列,也是等差数列.
2
同一个不 为零
q(q≠0)
讲授新知
二、等比中项
在两个数a,b中间插入一个数G,使a,G,b成等比数列,则G称为a与b的等比中项.
注释:只有当a、b同号时a、b才有等比中项,并且有两个等比中项,分别是与-;当a,b异号时没有等比中项.
讲授新知
三、等比数列的通项公式
(1)已知等比数列{an}的首项为a1,公比为q(q≠0),则数列{an}的通项公式为an=________.
(2)等比数列通项公式的推广:an=amqn-m,变形得qn-m=.
注释:等比数列的任意一项都可以由该数列的某一项和公比表示.
a1qn-1
讲授新知
四、等比数列与指数函数的关系
等比数列的通项公式可整理为an=·qn,而y=·qx(q≠1)是一个不为0的常数与指数函数qx的乘积,从图象上看,表示数列中的各项的点是函数y=·qx的图象上的孤立点.
讲授新知
题型1 等比数列通项公式的基本运算
例1 在等比数列{an}中,
(1)a4=2,a7=8,求an;
(2)a2+a5=18,a3+a6=9,an=1,求n.
例题讲解
解:设首项为a1,公比为q.
(1)方法一:
由得q3=4,q=,a1q3=2,
a1==,an=a1qn-1=.
方法二:a7=a4q3,q3=4,q=.
an=a4qn-4=2·()n-4=.
(2)方法一:
由得q=,a1=32,
又an=1, 32×()n-1=1.
26-n=20,n=6.
方法二:因为a3+a6=q(a2+a5),
所以q=.
由a1q+a1q4=18,知a1=32.
由an=a1qn-1=1,知n=6.
方法总结:
等比数列中求和的2种常用方法
1.根据已知条件,建立关于和的方程组,求出和后再求出;
2.充分利用各项之间的关系,直接求出后,再求出,最后求
题型2 等比中项的应用
例2 (1)已知等比数列的前3项依次为x,2x+2,3x+3,求实数x的值;
(2)已知等比数列{an},a2a3a4=64,a3+a6=36,求a2和a6的等比中项.
解:(1)因为等比数列的前3项依次为x,2x+2,3x+3,所以x(3x+3)=(2x+2)2,解得x=-1或x=-4.又因为当x=-1时,2x+2=3x+3=0不合题意,所以实数x的值为-4.
(2)因为{an}是等比数列,所以a3是a2和a4的等比中项,即=a2a4,所以=64,解得a3=4,从而a6=32.设{an}的公比为q,则解得所以a2=a1q=2.
设a2和a6的等比中项为G,则G2=a2a6=64,所以G=±8.
例题讲解
等比中项应用的注释
1.只有同号时, 的等比中项有两个; 异号时,没有等比中项;
2.在等比数列{an}中,偶数项同号,奇数项同号;
3. 成等比数列
题型3 灵活设元求解等比数列问题
例3 (1)有四个数成等比数列,将这四个数分别减去1,1,4,13成等差数列,则这四个数的和是________.
45
解:设这四个数分别为a,aq,aq2,aq3,
则a-1,aq-1,aq2-4,aq3-13成等差数列.
解得a=3,q=2.
这四个数分别是3,6,12,24,其和为45.
(2)有四个实数,前三个数成等比数列,且它们的乘积为216,后三个数成等差数列,且它们的和为12,求这四个数.
解:方法一:设前三个数分别为,a,aq,则·a·aq=216,
a3=216,a=6.
前三个数为,6,6q.
由题意知第4个数为12q-6.
6+6q+12q-6=12,解得q=.
故所求的四个数为9,6,4,2.
方法二:设后三个数为4-d,4,4+d,则第一个数为(4-d)2,
由题意知(4-d)2×(4-d)×4=216,解得4-d=6,d=-2.
故所求得的四个数为9,6,4,2.
几个数成等比数列的设法
1.三个数成等比数列设为,a,aq.
推广到一般:奇数个数成等比数列设为…,,a,aq,aq2,…
2.四个符号相同的数成等比数列设为,aq,aq3.
推广到一般:偶数个符号相同的数成等比数列设为…,,aq,aq3,aq5,…
3.四个数成等比数列,不能确定它们的符号是否相同时,可设为a,aq,aq2,aq3.
(1)若等比数列{an}满足a1+a2=3,a4+a5=81,则数列{an}的公比为( )
A.-2 B.2 C.-3 D.3
解:设等比数列{an}的公比为q,
a1+a2=3,a4+a5=81,
,
=,解得q=3,
故选D.
巩固练习
(2)如果-1,a,b,c,-9成等比数列,那么b=______,ac=_____.
-3
9
解:b是-1,-9的等比中项,b2=9,b=±3.
等比数列奇数项符号相同, b<0,b=-3,
b是a,c的等比中项,b2=ac,即ac=9.
巩固练习
(3)在2和20之间插入两个数,使前三个数成等比数列,后三个数成等差数列,则插入的两个数的和为( )
A.-4或 B.4或
C.4 D.
解:设插入的第一个数为a,则插入的另一个数为.
由a,,20成等差数列得2×=a+20.
∴a2-a-20=0,解得a=-4或a=5.
当a=-4时,插入的两个数的和为a+=4.
当a=5时,插入的两个数的和为a+=.
故选B.
巩固练习
课堂小结
1.数学思想:转化与化归,函数与方程;
2.数学知识:
等比数列的概念及其通项公式、等比中项、等比数列与指数函数的关系.
4.3.1等比数列的概念
一、等比数列的概念
(1)文字语言:一般地,如果一个数列从第_____项起,每一项与它的前一项的比都等于__________常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母________表示.
(2)符号语言:=q(q为常数,n∈N*)
注释:
1. 等比数列中不能出现0,公比不能为0;
2. 当q=1时,此时为常数列,也是等差数列.
2
同一个不 为零
q(q≠0)
讲授新知
二、等比中项
在两个数a,b中间插入一个数G,使a,G,b成等比数列,则G称为a与b的等比中项.
注释:只有当a、b同号时a、b才有等比中项,并且有两个等比中项,分别是与-;当a,b异号时没有等比中项.
讲授新知
三、等比数列的通项公式
(1)已知等比数列{an}的首项为a1,公比为q(q≠0),则数列{an}的通项公式为an=________.
(2)等比数列通项公式的推广:an=amqn-m,变形得qn-m=.
注释:等比数列的任意一项都可以由该数列的某一项和公比表示.
a1qn-1
讲授新知
四、等比数列与指数函数的关系
等比数列的通项公式可整理为an=·qn,而y=·qx(q≠1)是一个不为0的常数与指数函数qx的乘积,从图象上看,表示数列中的各项的点是函数y=·qx的图象上的孤立点.
讲授新知
题型1 等比数列通项公式的基本运算
例1 在等比数列{an}中,
(1)a4=2,a7=8,求an;
(2)a2+a5=18,a3+a6=9,an=1,求n.
例题讲解
解:设首项为a1,公比为q.
(1)方法一:
由得q3=4,q=,a1q3=2,
a1==,an=a1qn-1=.
方法二:a7=a4q3,q3=4,q=.
an=a4qn-4=2·()n-4=.
(2)方法一:
由得q=,a1=32,
又an=1, 32×()n-1=1.
26-n=20,n=6.
方法二:因为a3+a6=q(a2+a5),
所以q=.
由a1q+a1q4=18,知a1=32.
由an=a1qn-1=1,知n=6.
方法总结:
等比数列中求和的2种常用方法
1.根据已知条件,建立关于和的方程组,求出和后再求出;
2.充分利用各项之间的关系,直接求出后,再求出,最后求
题型2 等比中项的应用
例2 (1)已知等比数列的前3项依次为x,2x+2,3x+3,求实数x的值;
(2)已知等比数列{an},a2a3a4=64,a3+a6=36,求a2和a6的等比中项.
解:(1)因为等比数列的前3项依次为x,2x+2,3x+3,所以x(3x+3)=(2x+2)2,解得x=-1或x=-4.又因为当x=-1时,2x+2=3x+3=0不合题意,所以实数x的值为-4.
(2)因为{an}是等比数列,所以a3是a2和a4的等比中项,即=a2a4,所以=64,解得a3=4,从而a6=32.设{an}的公比为q,则解得所以a2=a1q=2.
设a2和a6的等比中项为G,则G2=a2a6=64,所以G=±8.
例题讲解
等比中项应用的注释
1.只有同号时, 的等比中项有两个; 异号时,没有等比中项;
2.在等比数列{an}中,偶数项同号,奇数项同号;
3. 成等比数列
题型3 灵活设元求解等比数列问题
例3 (1)有四个数成等比数列,将这四个数分别减去1,1,4,13成等差数列,则这四个数的和是________.
45
解:设这四个数分别为a,aq,aq2,aq3,
则a-1,aq-1,aq2-4,aq3-13成等差数列.
解得a=3,q=2.
这四个数分别是3,6,12,24,其和为45.
(2)有四个实数,前三个数成等比数列,且它们的乘积为216,后三个数成等差数列,且它们的和为12,求这四个数.
解:方法一:设前三个数分别为,a,aq,则·a·aq=216,
a3=216,a=6.
前三个数为,6,6q.
由题意知第4个数为12q-6.
6+6q+12q-6=12,解得q=.
故所求的四个数为9,6,4,2.
方法二:设后三个数为4-d,4,4+d,则第一个数为(4-d)2,
由题意知(4-d)2×(4-d)×4=216,解得4-d=6,d=-2.
故所求得的四个数为9,6,4,2.
几个数成等比数列的设法
1.三个数成等比数列设为,a,aq.
推广到一般:奇数个数成等比数列设为…,,a,aq,aq2,…
2.四个符号相同的数成等比数列设为,aq,aq3.
推广到一般:偶数个符号相同的数成等比数列设为…,,aq,aq3,aq5,…
3.四个数成等比数列,不能确定它们的符号是否相同时,可设为a,aq,aq2,aq3.
(1)若等比数列{an}满足a1+a2=3,a4+a5=81,则数列{an}的公比为( )
A.-2 B.2 C.-3 D.3
解:设等比数列{an}的公比为q,
a1+a2=3,a4+a5=81,
,
=,解得q=3,
故选D.
巩固练习
(2)如果-1,a,b,c,-9成等比数列,那么b=______,ac=_____.
-3
9
解:b是-1,-9的等比中项,b2=9,b=±3.
等比数列奇数项符号相同, b<0,b=-3,
b是a,c的等比中项,b2=ac,即ac=9.
巩固练习
(3)在2和20之间插入两个数,使前三个数成等比数列,后三个数成等差数列,则插入的两个数的和为( )
A.-4或 B.4或
C.4 D.
解:设插入的第一个数为a,则插入的另一个数为.
由a,,20成等差数列得2×=a+20.
∴a2-a-20=0,解得a=-4或a=5.
当a=-4时,插入的两个数的和为a+=4.
当a=5时,插入的两个数的和为a+=.
故选B.
巩固练习
课堂小结
1.数学思想:转化与化归,函数与方程;
2.数学知识:
等比数列的概念及其通项公式、等比中项、等比数列与指数函数的关系.
