人教版八年级上册数学11.2.2 三角形的外角 同步练习(含答案)
文档属性
| 名称 | 人教版八年级上册数学11.2.2 三角形的外角 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 207.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-11 10:57:21 | ||
图片预览



文档简介
11.2.2三角形的外角
选择题
如图所示, 一副三角板叠放在一起,则图中∠α等于()
A.105 B.115 C.120 D.135
如图,已知ABFE,∠ABC=70,∠CDE=150,则∠BCD的值为()
A.40 B.30 C.20 D.80
如图,等腰三角形ABC中,AB=AC,∠BAC=40,中线AD与角平分线CE交于点F,则∠CFD的度数为()
A.25 B.35 C.45 D.55
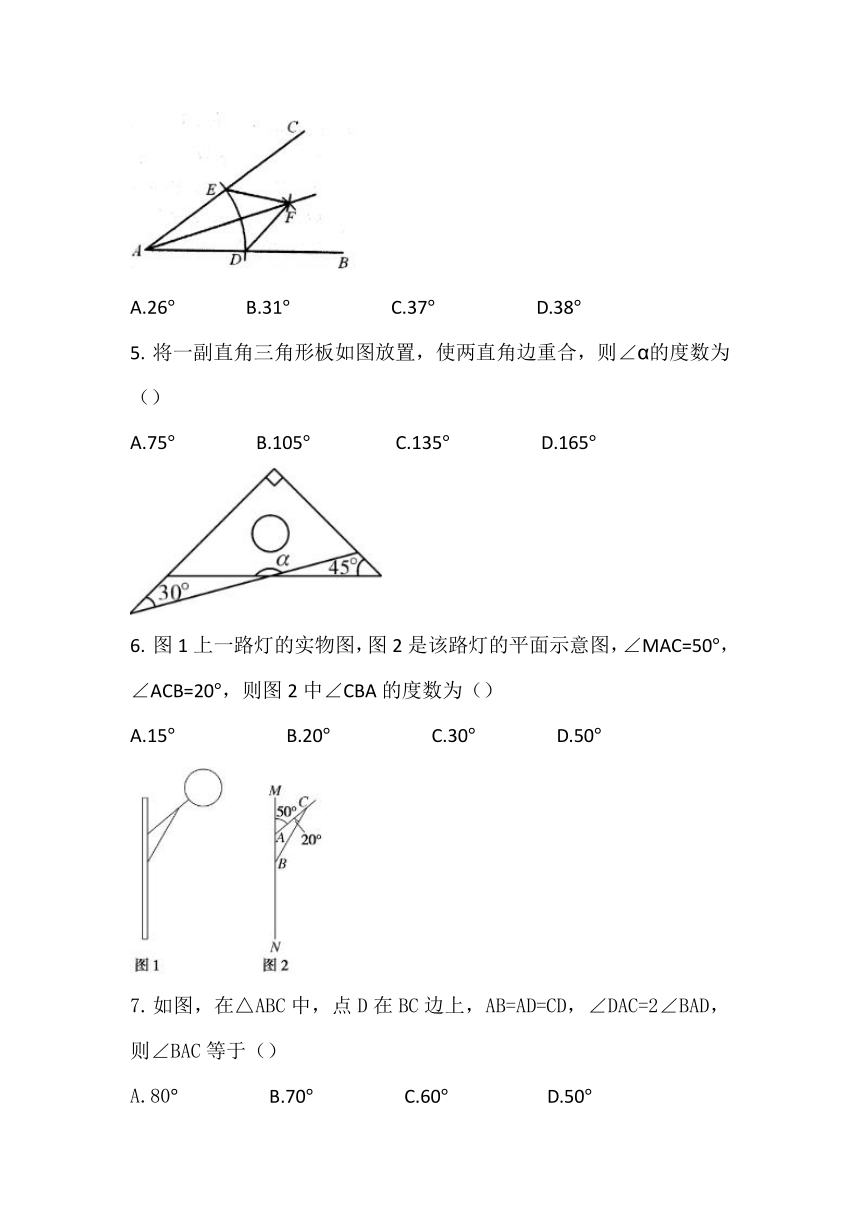
如图,小亮进行以下操作:以点A为圆心,适当长为半径作圆弧分别交AB,AC于点D,E;分别以点D,E为圆心 ,大于长为半径作圆弧,两条圆弧交于∠BAC内一点F,作射线AF. 若∠BDF=50,∠EFD-∠BAC=24,则∠BAC等于()
A.26 B.31 C.37 D.38
将一副直角三角形板如图放置,使两直角边重合,则∠α的度数为()
A.75 B.105 C.135 D.165
图1上一路灯的实物图,图2是该路灯的平面示意图,∠MAC=50,∠ACB=20,则图2中∠CBA的度数为()
A.15 B.20 C.30 D.50
如图,在△ABC中,点D在BC边上,AB=AD=CD,∠DAC=2∠BAD,则∠BAC等于()
A.80 B.70 C.60 D.50
如图,一束平行太阳光照射到正六边形上,若∠1=28,则∠2的大小为()
A.150 B.148 C.140 D.138
如图,△ABC中,∠CAB=∠CBA=48,点O为△ABC内一点,∠OAB=12,
∠OBC=18,则∠ACO=()
A.60 B.72 C.70 D.65
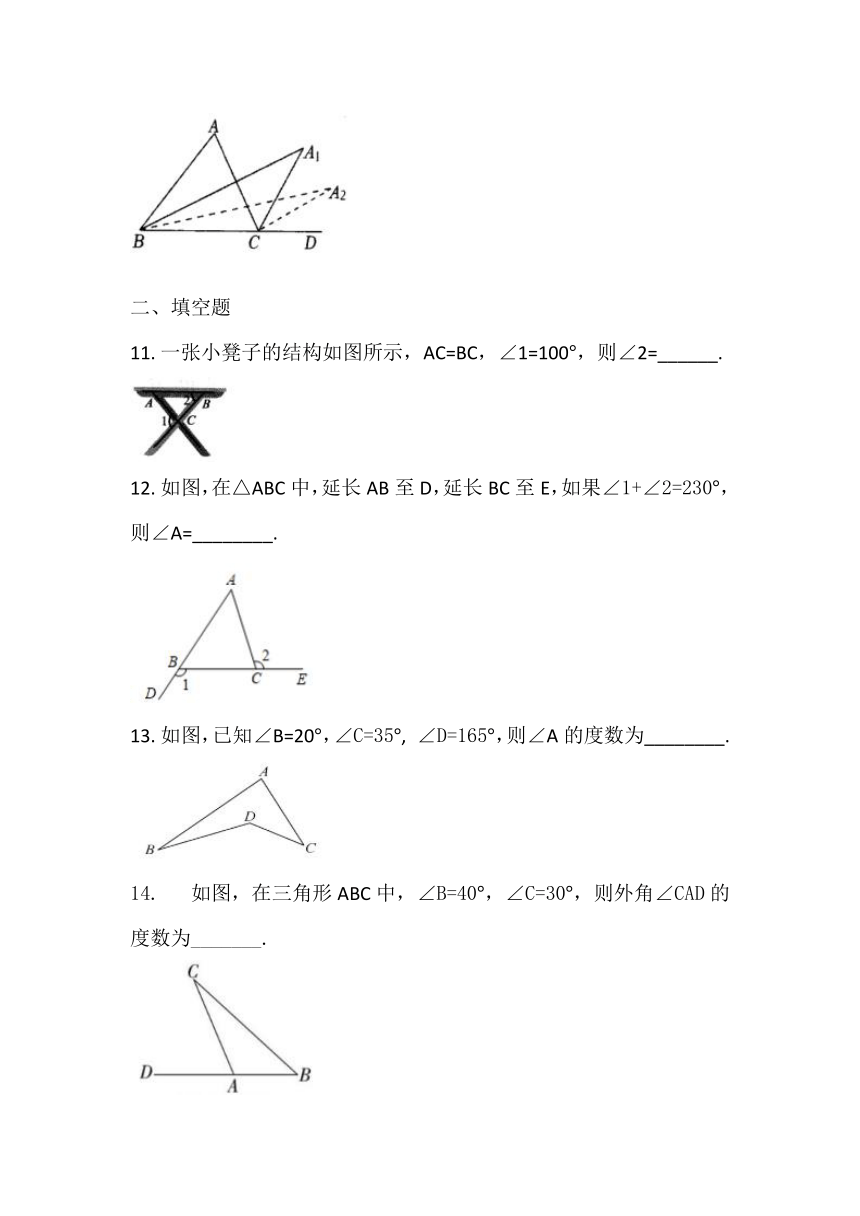
如图,D为△ABC边BC延长线上一点,∠ABC与∠ACD的平分线交于点A1,∠A1BC与∠A1CD的平分线交于点A2,,∠A2022BC与∠A2022CD的平分线交于点A2023,若∠A2023=α,则∠A的值为()
A.2022α B.2023α C.22022α D.22023α
填空题
一张小凳子的结构如图所示,AC=BC,∠1=100,则∠2=______.
如图,在△ABC中,延长AB至D,延长BC至E,如果∠1+∠2=230,
则∠A=________.
如图,已知∠B=20,∠C=35, ∠D=165,则∠A的度数为________.
如图,在三角形ABC中,∠B=40,∠C=30,则外角∠CAD的度数为_______.
生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多想不到的收获。如图是由一副三角板拼凑得到的,图中∠1=________.
如图,已知∠ABC=31,又△BAC的角平分线AE与∠BCA的外角平分线CE相交于E点,则∠AEC为________.
下图是可调躺椅示意图(数据如图),AE与BD的交点为C,且∠A,∠B,∠E保持不变,为了舒适,需调整∠D的大小,使∠EFD=110,则图中∠D应______(填“增加”或“减少”)____度。
如图,在△ABC中,∠A=64,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;依次类推,则∠A4=______度
解答题
将一副直角三角尺BAC和ADE如图放置,其中∠BAC=∠ADE=90,∠BCA=30,∠AED=45,若∠AFD=75,试判断AE与BC的位置关系,并说明 理由。
(1)如图①在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC=______(用α表示);如图②∠CBO=BC,∠BCO=CB, ∠A=α,则∠BOC=________(用α表示)
扩展探究:
如图③,∠CBO=BC,∠BCO=ECB,∠A=α,求∠BOC的度数(用α表示),并说明理由。
如图,△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC上,且∠ADE=∠AED,连接DE.
如图①,若∠B=∠C=30,∠BAD=70,求∠CDE的度数;
如图②,若∠ABC=∠ACB=70,∠CDE=15,求∠BAD的度数;
由(1)和(2)的结果知道∠CDE和∠BAD的数量关系是:______;
当点D在线段BC的延长线上时,上述关系式是否还成立?请直接写出结论.
参考答案
选择题
A 2.A 3.D 4.D 5.D 6.C 7.C 8.B 9.B 10.D
填空题
50 12.50 13.110 14.70 15. 105 16.15.5 17.减少10 18.4
解答题
解:AE∥BC,理由如下
∵∠AFD=∠E+∠FAE,∠AED=45,∠AFD=75
∴∠FAE=∠AFD-∠AED=30
∵∠BCA=30
∴∠FAE=∠BCA
∴AE∥BC
(1)①∠BOC=90+ ②∠BOC=120+α
∵∠BAC+∠ACB=∠DBC,∠CBO=DBC
∴∠CBO=
同理,得∠BCO=
∴∠CBO+∠BCO=AC+
又∵∠ACB+∠ABC=180∠BAC,∠BAC=α
∴∠CBO+∠BCO=+=60+α
∴∠BOC=180-(∠CBO+∠BCO)
=180-60-α
=120α
21.解:(1)∵∠B=∠C=30
∴∠BAC=180-(∠B+∠C)=120
又∵∠BAD=70
∴∠DAE=∠BAC-∠BAD=120-70=50
∵∠DAE+∠ADE+∠AED=180,∠ADE=∠AED
∴∠AED=
∵∠C+∠EDC=∠DEC
∴∠EDC=∠DEC-∠C=35
(2)∵∠ACD=∠CDE+∠E,∠ACB=70,∠CDE=15
∴∠E=70-15=55
∴∠ADE=∠AED=55
∵∠DAE+∠ADE+∠E=180
∴∠DAE=180-(∠ADE+∠E)=70
∵∠ABC+∠ACB+∠BAC=180
∴∠BAC=180-(∠ACB+∠ABC)=40
∴∠BAD=∠DAC-∠BAC=30
∠BAD=2∠CDE
当点D在线段BC的延长线上时,上述关系式仍然成立
选择题
如图所示, 一副三角板叠放在一起,则图中∠α等于()
A.105 B.115 C.120 D.135
如图,已知ABFE,∠ABC=70,∠CDE=150,则∠BCD的值为()
A.40 B.30 C.20 D.80
如图,等腰三角形ABC中,AB=AC,∠BAC=40,中线AD与角平分线CE交于点F,则∠CFD的度数为()
A.25 B.35 C.45 D.55
如图,小亮进行以下操作:以点A为圆心,适当长为半径作圆弧分别交AB,AC于点D,E;分别以点D,E为圆心 ,大于长为半径作圆弧,两条圆弧交于∠BAC内一点F,作射线AF. 若∠BDF=50,∠EFD-∠BAC=24,则∠BAC等于()
A.26 B.31 C.37 D.38
将一副直角三角形板如图放置,使两直角边重合,则∠α的度数为()
A.75 B.105 C.135 D.165
图1上一路灯的实物图,图2是该路灯的平面示意图,∠MAC=50,∠ACB=20,则图2中∠CBA的度数为()
A.15 B.20 C.30 D.50
如图,在△ABC中,点D在BC边上,AB=AD=CD,∠DAC=2∠BAD,则∠BAC等于()
A.80 B.70 C.60 D.50
如图,一束平行太阳光照射到正六边形上,若∠1=28,则∠2的大小为()
A.150 B.148 C.140 D.138
如图,△ABC中,∠CAB=∠CBA=48,点O为△ABC内一点,∠OAB=12,
∠OBC=18,则∠ACO=()
A.60 B.72 C.70 D.65
如图,D为△ABC边BC延长线上一点,∠ABC与∠ACD的平分线交于点A1,∠A1BC与∠A1CD的平分线交于点A2,,∠A2022BC与∠A2022CD的平分线交于点A2023,若∠A2023=α,则∠A的值为()
A.2022α B.2023α C.22022α D.22023α
填空题
一张小凳子的结构如图所示,AC=BC,∠1=100,则∠2=______.
如图,在△ABC中,延长AB至D,延长BC至E,如果∠1+∠2=230,
则∠A=________.
如图,已知∠B=20,∠C=35, ∠D=165,则∠A的度数为________.
如图,在三角形ABC中,∠B=40,∠C=30,则外角∠CAD的度数为_______.
生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多想不到的收获。如图是由一副三角板拼凑得到的,图中∠1=________.
如图,已知∠ABC=31,又△BAC的角平分线AE与∠BCA的外角平分线CE相交于E点,则∠AEC为________.
下图是可调躺椅示意图(数据如图),AE与BD的交点为C,且∠A,∠B,∠E保持不变,为了舒适,需调整∠D的大小,使∠EFD=110,则图中∠D应______(填“增加”或“减少”)____度。
如图,在△ABC中,∠A=64,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;依次类推,则∠A4=______度
解答题
将一副直角三角尺BAC和ADE如图放置,其中∠BAC=∠ADE=90,∠BCA=30,∠AED=45,若∠AFD=75,试判断AE与BC的位置关系,并说明 理由。
(1)如图①在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC=______(用α表示);如图②∠CBO=BC,∠BCO=CB, ∠A=α,则∠BOC=________(用α表示)
扩展探究:
如图③,∠CBO=BC,∠BCO=ECB,∠A=α,求∠BOC的度数(用α表示),并说明理由。
如图,△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC上,且∠ADE=∠AED,连接DE.
如图①,若∠B=∠C=30,∠BAD=70,求∠CDE的度数;
如图②,若∠ABC=∠ACB=70,∠CDE=15,求∠BAD的度数;
由(1)和(2)的结果知道∠CDE和∠BAD的数量关系是:______;
当点D在线段BC的延长线上时,上述关系式是否还成立?请直接写出结论.
参考答案
选择题
A 2.A 3.D 4.D 5.D 6.C 7.C 8.B 9.B 10.D
填空题
50 12.50 13.110 14.70 15. 105 16.15.5 17.减少10 18.4
解答题
解:AE∥BC,理由如下
∵∠AFD=∠E+∠FAE,∠AED=45,∠AFD=75
∴∠FAE=∠AFD-∠AED=30
∵∠BCA=30
∴∠FAE=∠BCA
∴AE∥BC
(1)①∠BOC=90+ ②∠BOC=120+α
∵∠BAC+∠ACB=∠DBC,∠CBO=DBC
∴∠CBO=
同理,得∠BCO=
∴∠CBO+∠BCO=AC+
又∵∠ACB+∠ABC=180∠BAC,∠BAC=α
∴∠CBO+∠BCO=+=60+α
∴∠BOC=180-(∠CBO+∠BCO)
=180-60-α
=120α
21.解:(1)∵∠B=∠C=30
∴∠BAC=180-(∠B+∠C)=120
又∵∠BAD=70
∴∠DAE=∠BAC-∠BAD=120-70=50
∵∠DAE+∠ADE+∠AED=180,∠ADE=∠AED
∴∠AED=
∵∠C+∠EDC=∠DEC
∴∠EDC=∠DEC-∠C=35
(2)∵∠ACD=∠CDE+∠E,∠ACB=70,∠CDE=15
∴∠E=70-15=55
∴∠ADE=∠AED=55
∵∠DAE+∠ADE+∠E=180
∴∠DAE=180-(∠ADE+∠E)=70
∵∠ABC+∠ACB+∠BAC=180
∴∠BAC=180-(∠ACB+∠ABC)=40
∴∠BAD=∠DAC-∠BAC=30
∠BAD=2∠CDE
当点D在线段BC的延长线上时,上述关系式仍然成立
