第十八章 平行四边形 专项提升学案(含答案) 人教版数学八年级下册
文档属性
| 名称 | 第十八章 平行四边形 专项提升学案(含答案) 人教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 381.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-11 10:55:49 | ||
图片预览

文档简介
第十八章 平行四边形
知识梳理
1、平行四边形:两组对边分别平行的四边形叫做平行四边形。平行四边形用符号“□ABCD”表示,如平行四边形ABCD记作“□ABCD”,读作“平行四边形ABCD”。
(1)平行四边形的性质:
①平行四边形的对边平行且相等;
②平行四边形的对角相等;
③平行四边形的对角线互相平分。
(2)平行四边形的判定:
①两组对边分别平行的四边形是平行四边形
②两组对边分别相等的四边形是平行四边形;
③两组对角分别相等的四边形是平行四边形;
④对角线互相平分的四边形是平行四边形;
⑤一组对边平行且相等的四边形是平行四边形。
2、矩形:有一个角是直角的平行四边形叫做矩形。
(1)矩形的性质:
①矩形具有平行四边形的一切性质;矩形的四个角都是直角;矩形的对角线相等。
②推论:直角三角形斜边上的中线等于斜边的一半。
(2)矩形的判定:
①有一个角是直角的平行四边形是矩形;
②对角线相等的平行四边形是矩形;
③有三个角是直角的四边形是矩形。
4、菱形:有一组邻边相等的平行四边形叫做菱形。
(1)菱形的性质:
①菱形具有平行四边形的一切性质;
②菱形的四条边都相等;
③菱形的两条对角线互相垂直,并且每一条对角线都平分一组对角。
(2)菱形的判定:
①一组邻边相等的平行四边形是菱形;
②对角线互相垂直的平行四边形是菱形;
③四条边相等的四边形是菱形。
(3)菱形的面积:
S菱形=底边长×高=两条对角线乘积的一半
5、正方形:
正方形是最特殊的四边形,它具有矩形的性质,也具有菱形的性质。
提升练习
一、选择题
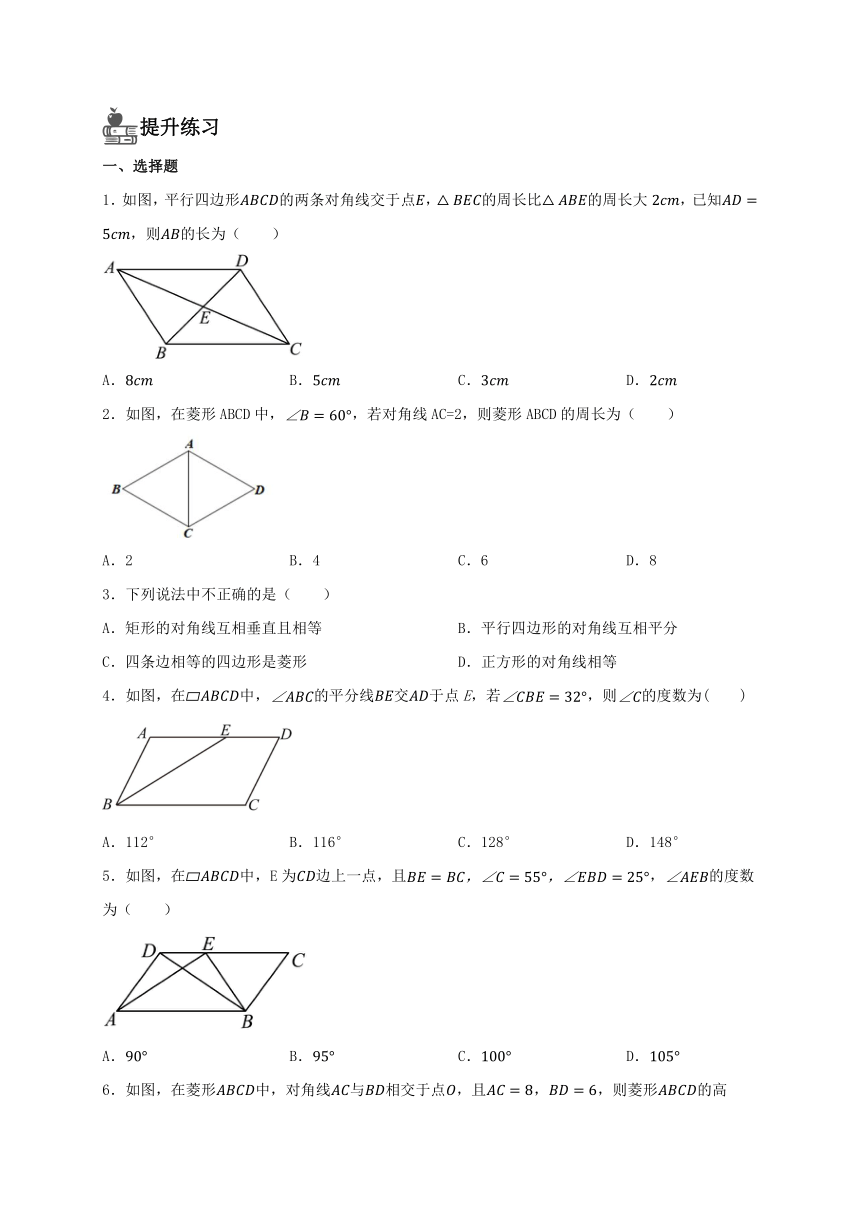
1.如图,平行四边形的两条对角线交于点,的周长比的周长大,已知,则的长为( )
A. B. C. D.
2.如图,在菱形ABCD中,,若对角线AC=2,则菱形ABCD的周长为( )
A.2 B.4 C.6 D.8
3.下列说法中不正确的是( )
A.矩形的对角线互相垂直且相等 B.平行四边形的对角线互相平分
C.四条边相等的四边形是菱形 D.正方形的对角线相等
4.如图,在中,的平分线交于点E,若,则的度数为( )
A.112° B.116° C.128° D.148°
5.如图,在中,E为边上一点,且,的度数为( )
A. B. C. D.
6.如图,在菱形中,对角线与相交于点,且,,则菱形的高( )
A. B. C. D.
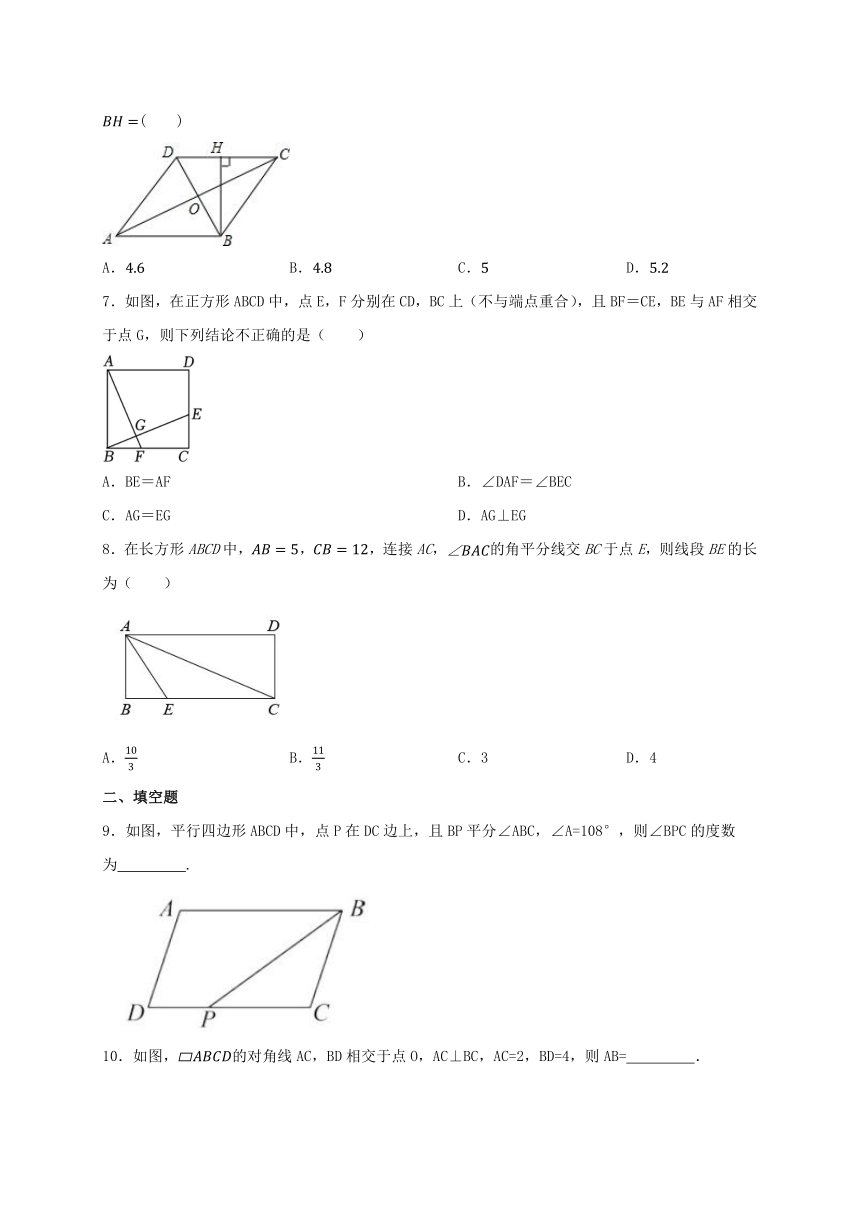
7.如图,在正方形ABCD中,点E,F分别在CD,BC上(不与端点重合),且BF=CE,BE与AF相交于点G,则下列结论不正确的是( )
A.BE=AF B.∠DAF=∠BEC
C.AG=EG D.AG⊥EG
8.在长方形ABCD中,,,连接AC,的角平分线交BC于点E,则线段BE的长为( )
A. B. C.3 D.4
二、填空题
9.如图,平行四边形ABCD中,点P在DC边上,且BP平分∠ABC,∠A=108°,则∠BPC的度数为 .
10.如图,的对角线AC,BD相交于点O,AC⊥BC,AC=2,BD=4,则AB= .
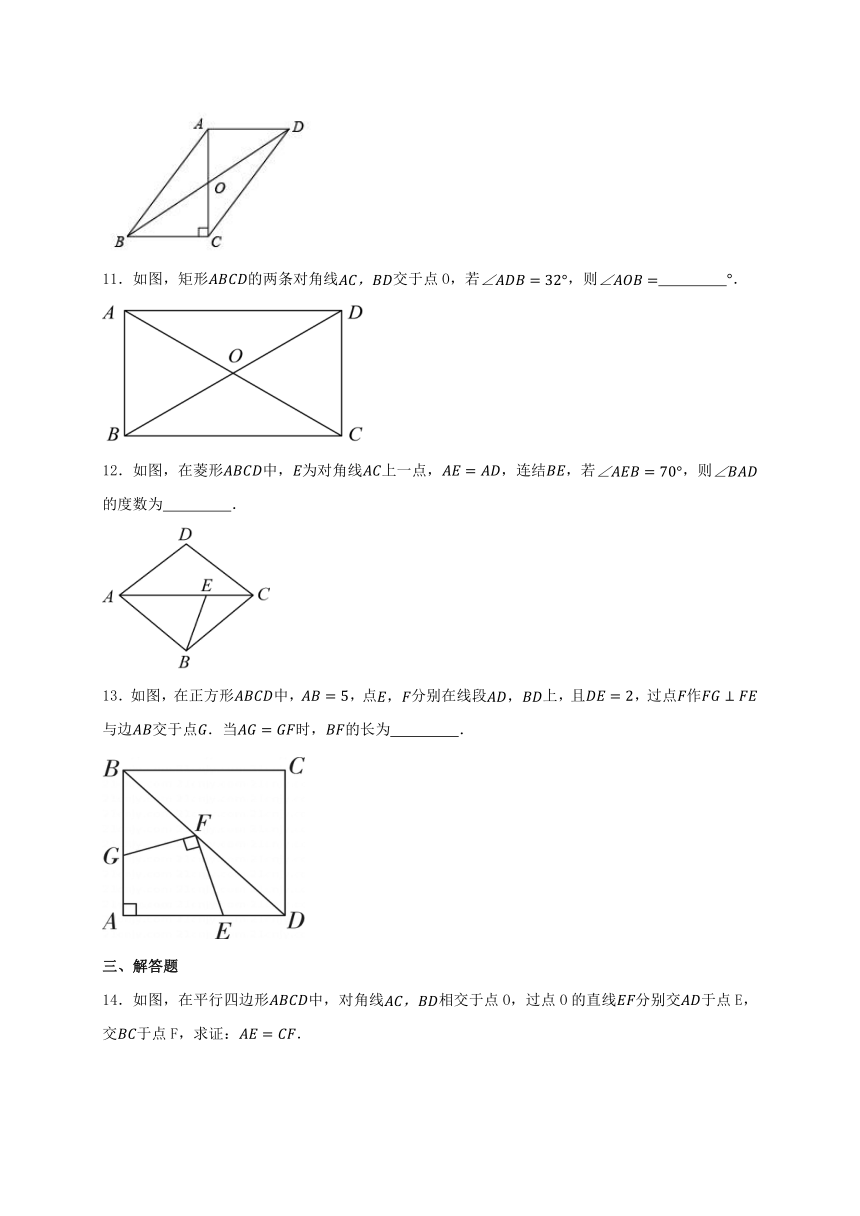
11.如图,矩形的两条对角线交于点O,若,则 .
12.如图,在菱形中,为对角线上一点,,连结,若,则的度数为 .
13.如图,在正方形中,,点分别在线段上,且,过点作与边交于点.当时,的长为 .
三、解答题
14.如图,在平行四边形中,对角线相交于点O,过点O的直线分别交于点E,交于点F,求证:.
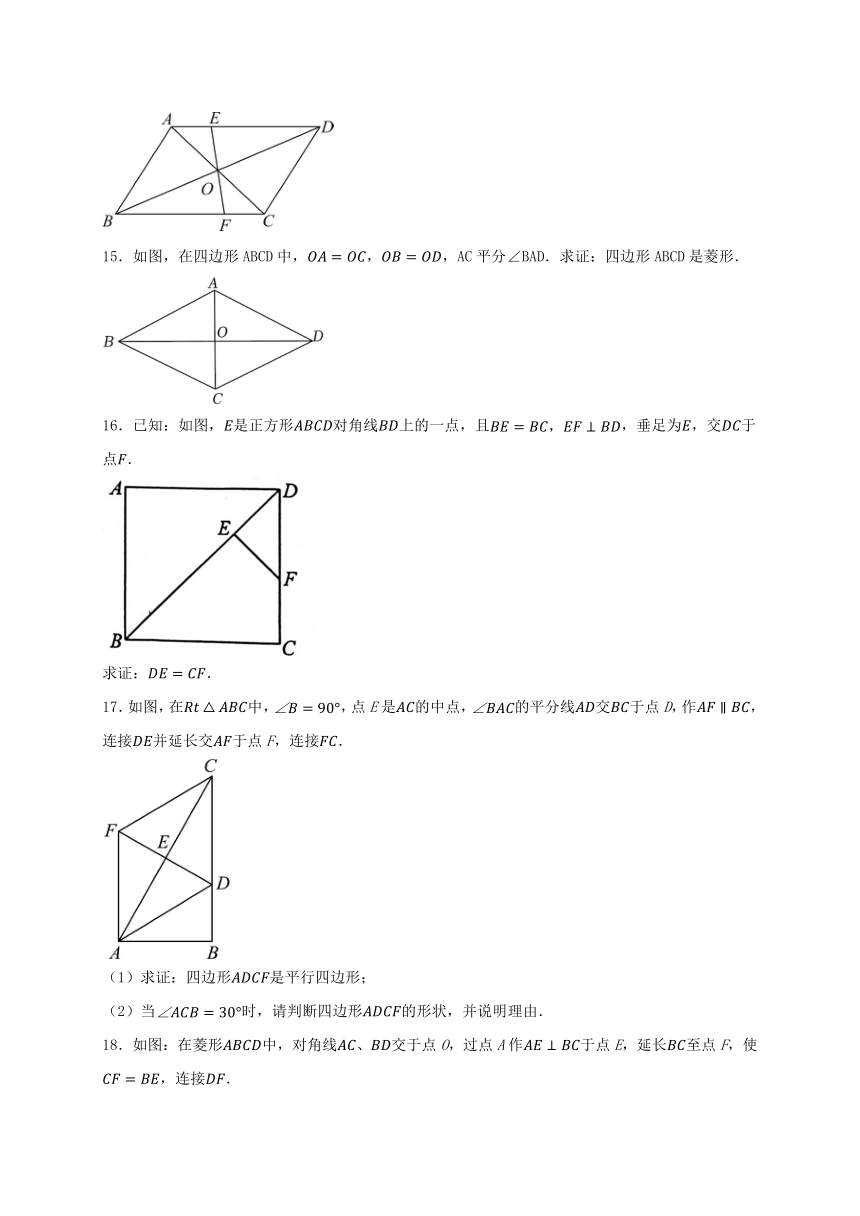
15.如图,在四边形ABCD中,,,AC平分∠BAD.求证:四边形ABCD是菱形.
16.已知:如图,是正方形对角线上的一点,且,垂足为,交于点.
求证:.
17.如图,在中,,点E是的中点,的平分线交于点D,作,连接并延长交于点F,连接.
(1)求证:四边形是平行四边形;
(2)当时,请判断四边形的形状,并说明理由.
18.如图:在菱形中,对角线、交于点O,过点A作于点E,延长至点F,使,连接.
(1)求证:四边形是矩形;
(2)若,,连接,求的长.
19.如图,在中,是边上的一点,是的中点,过点作的平行线交的延长线于点,且,连接.
(1)求证:;
(2)当满足什么条件时,四边形是菱形.
参考答案
1.C
2.D
3.A
4.B
5.B
6.B
7.C
8.A
9.36°
10.
11.64
12.80°
13.
14.证明:∵在平行四边形中,对角线相交于点O,
∴,
∴,
∴,
∴.
15.证明:,,
四边形是平行四边形,
,
,
平分,
,
,
,
四边形是菱形.
16.证明:连接BF,
∵四边形ABCD是正方形,EF⊥BD,
∴∠C=∠BEF=90°,∠EDF=45°
∴∠EFD=45°,即∠EDF=∠EFD,
∴DE=EF,
∵BE=BC,
∴Rt△BEF≌Rt△BCF(HL)
∴EF=CF,
∴DE=CF;
17.(1)证明:∵,
∴,
∵E是的中点,
∴,
在和中,
,
∴,
∴,
∵,
∴四边形是平行四边形.
(2)当时,四边形是菱形,理由如下:
∵,时,
∴,
∵平分,
∴,
∴,
由(1)可知四边形是平行四边形,
∴平行四边形是菱形.
18.(1)证明:在菱形中,,
,
∵,
∴,
∴,
∴,
∵,
∴四边形是平行四边形,
∵,
∴平行四边形是矩形;
(2)解:∵在矩形中,,
在中,,
又∵在菱形中,对角线、交于点O,
∴点为的中点,
∴.
19.(1)证明:∵是的中点,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴.
(2)当时,四边形是菱形.
证明:∵,,
∴四边形是平行四边形,
∵,,
∴,
∴四边形是菱形.
知识梳理
1、平行四边形:两组对边分别平行的四边形叫做平行四边形。平行四边形用符号“□ABCD”表示,如平行四边形ABCD记作“□ABCD”,读作“平行四边形ABCD”。
(1)平行四边形的性质:
①平行四边形的对边平行且相等;
②平行四边形的对角相等;
③平行四边形的对角线互相平分。
(2)平行四边形的判定:
①两组对边分别平行的四边形是平行四边形
②两组对边分别相等的四边形是平行四边形;
③两组对角分别相等的四边形是平行四边形;
④对角线互相平分的四边形是平行四边形;
⑤一组对边平行且相等的四边形是平行四边形。
2、矩形:有一个角是直角的平行四边形叫做矩形。
(1)矩形的性质:
①矩形具有平行四边形的一切性质;矩形的四个角都是直角;矩形的对角线相等。
②推论:直角三角形斜边上的中线等于斜边的一半。
(2)矩形的判定:
①有一个角是直角的平行四边形是矩形;
②对角线相等的平行四边形是矩形;
③有三个角是直角的四边形是矩形。
4、菱形:有一组邻边相等的平行四边形叫做菱形。
(1)菱形的性质:
①菱形具有平行四边形的一切性质;
②菱形的四条边都相等;
③菱形的两条对角线互相垂直,并且每一条对角线都平分一组对角。
(2)菱形的判定:
①一组邻边相等的平行四边形是菱形;
②对角线互相垂直的平行四边形是菱形;
③四条边相等的四边形是菱形。
(3)菱形的面积:
S菱形=底边长×高=两条对角线乘积的一半
5、正方形:
正方形是最特殊的四边形,它具有矩形的性质,也具有菱形的性质。
提升练习
一、选择题
1.如图,平行四边形的两条对角线交于点,的周长比的周长大,已知,则的长为( )
A. B. C. D.
2.如图,在菱形ABCD中,,若对角线AC=2,则菱形ABCD的周长为( )
A.2 B.4 C.6 D.8
3.下列说法中不正确的是( )
A.矩形的对角线互相垂直且相等 B.平行四边形的对角线互相平分
C.四条边相等的四边形是菱形 D.正方形的对角线相等
4.如图,在中,的平分线交于点E,若,则的度数为( )
A.112° B.116° C.128° D.148°
5.如图,在中,E为边上一点,且,的度数为( )
A. B. C. D.
6.如图,在菱形中,对角线与相交于点,且,,则菱形的高( )
A. B. C. D.
7.如图,在正方形ABCD中,点E,F分别在CD,BC上(不与端点重合),且BF=CE,BE与AF相交于点G,则下列结论不正确的是( )
A.BE=AF B.∠DAF=∠BEC
C.AG=EG D.AG⊥EG
8.在长方形ABCD中,,,连接AC,的角平分线交BC于点E,则线段BE的长为( )
A. B. C.3 D.4
二、填空题
9.如图,平行四边形ABCD中,点P在DC边上,且BP平分∠ABC,∠A=108°,则∠BPC的度数为 .
10.如图,的对角线AC,BD相交于点O,AC⊥BC,AC=2,BD=4,则AB= .
11.如图,矩形的两条对角线交于点O,若,则 .
12.如图,在菱形中,为对角线上一点,,连结,若,则的度数为 .
13.如图,在正方形中,,点分别在线段上,且,过点作与边交于点.当时,的长为 .
三、解答题
14.如图,在平行四边形中,对角线相交于点O,过点O的直线分别交于点E,交于点F,求证:.
15.如图,在四边形ABCD中,,,AC平分∠BAD.求证:四边形ABCD是菱形.
16.已知:如图,是正方形对角线上的一点,且,垂足为,交于点.
求证:.
17.如图,在中,,点E是的中点,的平分线交于点D,作,连接并延长交于点F,连接.
(1)求证:四边形是平行四边形;
(2)当时,请判断四边形的形状,并说明理由.
18.如图:在菱形中,对角线、交于点O,过点A作于点E,延长至点F,使,连接.
(1)求证:四边形是矩形;
(2)若,,连接,求的长.
19.如图,在中,是边上的一点,是的中点,过点作的平行线交的延长线于点,且,连接.
(1)求证:;
(2)当满足什么条件时,四边形是菱形.
参考答案
1.C
2.D
3.A
4.B
5.B
6.B
7.C
8.A
9.36°
10.
11.64
12.80°
13.
14.证明:∵在平行四边形中,对角线相交于点O,
∴,
∴,
∴,
∴.
15.证明:,,
四边形是平行四边形,
,
,
平分,
,
,
,
四边形是菱形.
16.证明:连接BF,
∵四边形ABCD是正方形,EF⊥BD,
∴∠C=∠BEF=90°,∠EDF=45°
∴∠EFD=45°,即∠EDF=∠EFD,
∴DE=EF,
∵BE=BC,
∴Rt△BEF≌Rt△BCF(HL)
∴EF=CF,
∴DE=CF;
17.(1)证明:∵,
∴,
∵E是的中点,
∴,
在和中,
,
∴,
∴,
∵,
∴四边形是平行四边形.
(2)当时,四边形是菱形,理由如下:
∵,时,
∴,
∵平分,
∴,
∴,
由(1)可知四边形是平行四边形,
∴平行四边形是菱形.
18.(1)证明:在菱形中,,
,
∵,
∴,
∴,
∴,
∵,
∴四边形是平行四边形,
∵,
∴平行四边形是矩形;
(2)解:∵在矩形中,,
在中,,
又∵在菱形中,对角线、交于点O,
∴点为的中点,
∴.
19.(1)证明:∵是的中点,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴.
(2)当时,四边形是菱形.
证明:∵,,
∴四边形是平行四边形,
∵,,
∴,
∴四边形是菱形.
