数学人教A版(2019)选择性必修第一册3.1.1椭圆及其标准方程 课件(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册3.1.1椭圆及其标准方程 课件(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 18:20:24 | ||
图片预览






文档简介
(共20张PPT)
椭圆及其标准方程
3.1.1
中国国家大剧院
中国国家大剧院造型新颖、前卫,构思独特,庞大的椭圆外形在长安街上显得像个“天外来客” 。这座“城市中的剧院、剧院中的城市”以一颗献给新世纪的超越想象的“湖中明珠”的奇异姿态出现。
圆锥曲线应用广泛与科研、生产以及人类生活有着密切的联系。
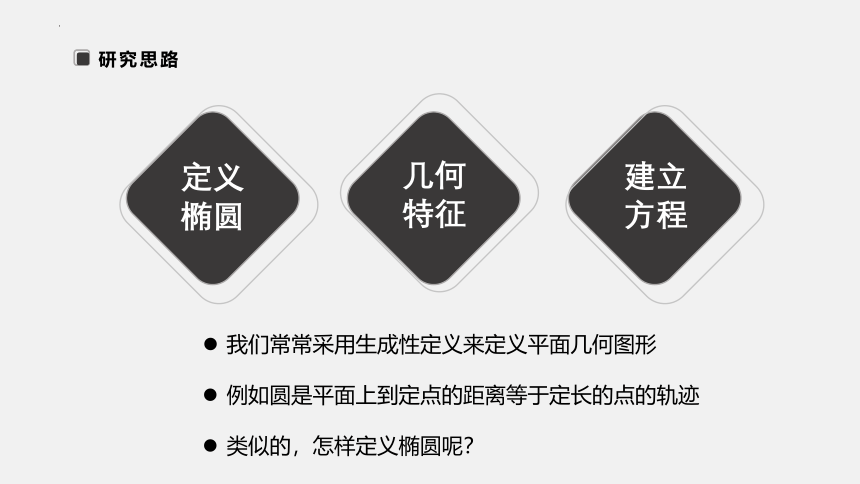
建立方程
几何特征
定义椭圆
研究思路
我们常常采用生成性定义来定义平面几何图形
例如圆是平面上到定点的距离等于定长的点的轨迹
类似的,怎样定义椭圆呢?
生成性定义
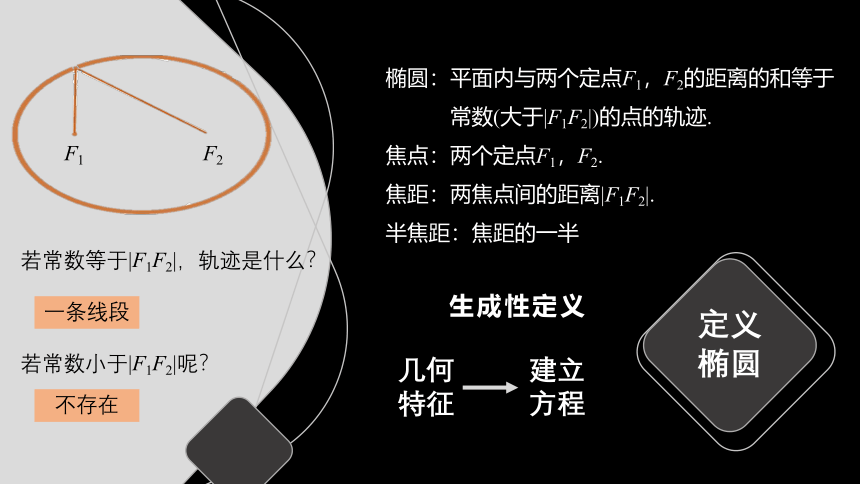
椭圆:平面内与两个定点F1,F2的距离的和等于
常数(大于|F1F2|)的点的轨迹.
焦点:两个定点F1,F2.
焦距:两焦点间的距离|F1F2|.
半焦距:焦距的一半
定义椭圆
F1 F2
建立方程
几何特征
若常数等于|F1F2|,轨迹是什么?
若常数小于|F1F2|呢?
一条线段
不存在
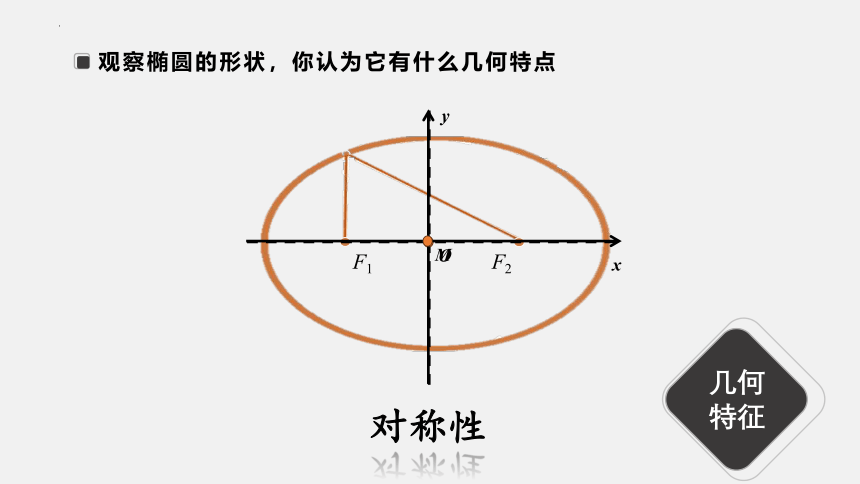
对称性
观察椭圆的形状,你认为它有什么几何特点
F1 F2
M
O
x
y
几何特征
建立方程
设P(x, y)是椭圆上任意一点,椭圆的焦距2c(c>0),P与F1和F2的距离的和等于正常数2a (2a>2c) ,则F1、F2的坐标分别是( c,0)、(c,0) .
求动点P的轨迹方程.
解:由椭圆的定义得:
又因为
得:
解得:
建立方程
设P(x, y)是椭圆上任意一点,椭圆的焦距2c(c>0),P与F1和F2的距离的和等于正常数2a (2a>2c) ,则F1、F2的坐标分别是( c,0)、(c,0) .
求动点P的轨迹方程.
解得:
因为 即 ,故
设
则
你能从中找出表示a、c、b的线段吗?
椭圆的标准方程
是焦点在y轴上的椭圆的标准方程
思考
它所表示的椭圆的焦点在x轴上,焦点是 ,中心在坐标原点的椭圆方程 ,其中
如果椭圆的焦点在y轴上,那么椭圆的标准方程是什么?
只要将方程中 的 x 和 y 调换,即可得
思考:能否根据椭圆的标准方程,判定焦点位置?
焦点在x轴上 焦点在y轴上
标准方程 _________________ _________________
焦点坐标 ____________________ ____________________
a,b,c的关系 __________ F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
b2=a2-c2
椭圆的标准方程
焦点位置
思考:能否根据椭圆的标准方程,判定焦点位置?
椭圆的焦点在x轴上 标准方程中含x2项的分母较大;
椭圆的焦点在y轴上 标准方程中含y2项的分母较大.
新知巩固
XIN ZHI GONG GU
1.平面内到点F1(-4,0),F2(4,0)距离相等的点的轨迹是椭圆.( )
2.到平面内两个定点的距离之和等于定长的点的轨迹叫做椭圆.( )
3.椭圆标准方程只与椭圆的形状、大小有关,与位置无关.( )
4.椭圆的两种标准形式中,虽然焦点位置不同,但都满足a2=b2+c2.( )
×
×
×
√
5.椭圆的焦点是 , ,焦距是 .
8
(-8,0) (8,0)
16
求椭圆的标准方程
QIU TUO YUAN DE BIAO ZHUN FANG CHENG
例1 求适合下列条件的椭圆的标准方程.
(1)焦点在y轴上,且经过两个点(0,2)和(1,0);
解 ∵椭圆的焦点在y轴上,
待定系数法
设标准方程
代入点求出a和b
注意判断标准方程的形式,看清焦点在哪里
除了待定系数法,还能用其他方法求它的标准方程吗?
求椭圆的标准方程
QIU TUO YUAN DE BIAO ZHUN FANG CHENG
例1 求适合下列条件的椭圆的标准方程.
(1)焦点在y轴上,且经过两个点(0,2)和(1,0);
解 ∵椭圆的焦点在y轴上,
待定系数法
设标准方程
代入点求出a和b
注意判断标准方程的形式,看清焦点在哪里.
另解 ∵椭圆的焦点在y轴上,
且经过两个点(0,2)和(1,0)
∴a=2,b=1
求椭圆的标准方程
QIU TUO YUAN DE BIAO ZHUN FANG CHENG
(2)两个焦点的坐标分别是(0,-2),(0,2),并且椭圆经过点;
解 ∵椭圆的焦点在y轴上,
又c=2,∴b2=a2-c2=6,
待定系数法
设标准方程
代入点求出a和b
定义法
设标准方程
根据定义求出a和b
两者结合
求椭圆的标准方程
QIU TUO YUAN DE BIAO ZHUN FANG CHENG
(3)经过点A和点B ;
解 ①当椭圆的焦点在x轴上时,
待定系数法
设标准方程
代入点求出a和b
注意此时需要根据焦点的位置分类讨论
②当椭圆的焦点在y轴上时,
能否避免分类讨论?
求椭圆的标准方程
QIU TUO YUAN DE BIAO ZHUN FANG CHENG
(3)经过点A和点B ;
解
待定系数法
设标准方程
代入点求出a和b
当焦点位置不确定时,可设椭圆方程为:
+ n
(m≠n,m>0,n>0).
从而避免分类讨论.
动点的轨迹问题
DONG DIAN DE GUI JI WEN TI
例2 在圆上任取一点P,过点P作x轴的垂线段PD,D为垂足,求PD的中点M的轨迹方程;
解 设点M的坐标为,点P的坐标为,
则点D的坐标为.
∵M是线段PD的中点∴,.
又∵点 P 在圆上
∴
即
整理得
求动点的轨迹的思路
直接求解:根据条件写出x与y 的关系式并整理化简。
定义求解:动点运动的几何条件满足某种已知曲线的定义,待定系数法求出轨迹方程。
联系相关点:联系另一个动点在运动中所遵循的条件中去求解。
动点的轨迹问题
DONG DIAN DE GUI JI WEN TI
例3 设A ,B ,直线AM,BM相交于点M,且它们的斜率之积是,求点M的轨迹方程;
解 设点M的坐标为
求动点的轨迹的思路
直接求解:根据条件写出x与y 的关系式并整理化简。
定义求解:动点运动的几何条件满足某种已知曲线的定义,待定系数法求出轨迹方程。
联系相关点:联系另一个动点在运动中所遵循的条件中去求解。
∵ A∴直线AM的斜率是
同理,直线BM的斜率是
由题得
整理得
即点M的轨迹是除去和两点的椭圆
——练一练
解焦点三角形
JIE JIAO DIAN SAN JIAO XING
例4.1 经过椭圆上的右焦点F2作垂直于x轴的直线AB,交椭圆于A、B两点,F1是椭圆的左焦点,求AF1B的周长
椭圆上一点P与椭圆的两个焦点F1,F2构成的△PF1F2,称为焦点三角形。
|PF1|+|PF2|=2a
解三角形方法:
勾股定理
正弦、余弦定理等
解 由题意, AF1B的周长为:
++ AB
++ AF2 +BF2
+ AF2 ++BF2
又∵ 点A、B在椭圆上
+ = 5=20
即AF1B的周长为20.
追问 :若直线AB不垂直于x轴, AF1B的周长有什么变化?
原因是什么?
6
由此也可看出, AF1B的周长与直线AB是否垂直于x轴无关.
解焦点三角形
JIE JIAO DIAN SAN JIAO XING
例4.2 已知P为椭圆上一点,F1,F2是椭圆的焦点,∠F1PF2=60°,求F1PF2的面积.
∴|F1F2|=2c=6,
在△PF1F2中,|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|cos 60°,
即36=|PF1|2+|PF2|2-|PF1|·|PF2|. ①
即48=|PF1|2+|PF2|2+2|PF1|·|PF2|. ②
由①②得|PF1|·|PF2|=4.
椭圆上一点P与椭圆的两个焦点F1,F2构成的△PF1F2,称为焦点三角形。
|PF1|+|PF2|=2a
解三角形方法:
勾股定理
正弦、余弦定理等
解焦点三角形
JIE JIAO DIAN SAN JIAO XING
例4 已知P为椭圆上一点,F1,F2是椭圆的焦点,∠F1PF2=60°,求F1PF2的面积.
∴|F1F2|=2c=6,
在△PF1F2中,|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|cos 60°,
即36=|PF1|2+|PF2|2-|PF1|·|PF2|. ①
即48=|PF1|2+|PF2|2+2|PF1|·|PF2|. ②
由①②得|PF1|·|PF2|=4.
∠PF1F2=90°
在△PF1F2中,由勾股定理知|PF2|2=|PF1|2+|F1F2|2,
即|PF2|2=|PF1|2+36,
椭圆及其标准方程
3.1.1
中国国家大剧院
中国国家大剧院造型新颖、前卫,构思独特,庞大的椭圆外形在长安街上显得像个“天外来客” 。这座“城市中的剧院、剧院中的城市”以一颗献给新世纪的超越想象的“湖中明珠”的奇异姿态出现。
圆锥曲线应用广泛与科研、生产以及人类生活有着密切的联系。
建立方程
几何特征
定义椭圆
研究思路
我们常常采用生成性定义来定义平面几何图形
例如圆是平面上到定点的距离等于定长的点的轨迹
类似的,怎样定义椭圆呢?
生成性定义
椭圆:平面内与两个定点F1,F2的距离的和等于
常数(大于|F1F2|)的点的轨迹.
焦点:两个定点F1,F2.
焦距:两焦点间的距离|F1F2|.
半焦距:焦距的一半
定义椭圆
F1 F2
建立方程
几何特征
若常数等于|F1F2|,轨迹是什么?
若常数小于|F1F2|呢?
一条线段
不存在
对称性
观察椭圆的形状,你认为它有什么几何特点
F1 F2
M
O
x
y
几何特征
建立方程
设P(x, y)是椭圆上任意一点,椭圆的焦距2c(c>0),P与F1和F2的距离的和等于正常数2a (2a>2c) ,则F1、F2的坐标分别是( c,0)、(c,0) .
求动点P的轨迹方程.
解:由椭圆的定义得:
又因为
得:
解得:
建立方程
设P(x, y)是椭圆上任意一点,椭圆的焦距2c(c>0),P与F1和F2的距离的和等于正常数2a (2a>2c) ,则F1、F2的坐标分别是( c,0)、(c,0) .
求动点P的轨迹方程.
解得:
因为 即 ,故
设
则
你能从中找出表示a、c、b的线段吗?
椭圆的标准方程
是焦点在y轴上的椭圆的标准方程
思考
它所表示的椭圆的焦点在x轴上,焦点是 ,中心在坐标原点的椭圆方程 ,其中
如果椭圆的焦点在y轴上,那么椭圆的标准方程是什么?
只要将方程中 的 x 和 y 调换,即可得
思考:能否根据椭圆的标准方程,判定焦点位置?
焦点在x轴上 焦点在y轴上
标准方程 _________________ _________________
焦点坐标 ____________________ ____________________
a,b,c的关系 __________ F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
b2=a2-c2
椭圆的标准方程
焦点位置
思考:能否根据椭圆的标准方程,判定焦点位置?
椭圆的焦点在x轴上 标准方程中含x2项的分母较大;
椭圆的焦点在y轴上 标准方程中含y2项的分母较大.
新知巩固
XIN ZHI GONG GU
1.平面内到点F1(-4,0),F2(4,0)距离相等的点的轨迹是椭圆.( )
2.到平面内两个定点的距离之和等于定长的点的轨迹叫做椭圆.( )
3.椭圆标准方程只与椭圆的形状、大小有关,与位置无关.( )
4.椭圆的两种标准形式中,虽然焦点位置不同,但都满足a2=b2+c2.( )
×
×
×
√
5.椭圆的焦点是 , ,焦距是 .
8
(-8,0) (8,0)
16
求椭圆的标准方程
QIU TUO YUAN DE BIAO ZHUN FANG CHENG
例1 求适合下列条件的椭圆的标准方程.
(1)焦点在y轴上,且经过两个点(0,2)和(1,0);
解 ∵椭圆的焦点在y轴上,
待定系数法
设标准方程
代入点求出a和b
注意判断标准方程的形式,看清焦点在哪里
除了待定系数法,还能用其他方法求它的标准方程吗?
求椭圆的标准方程
QIU TUO YUAN DE BIAO ZHUN FANG CHENG
例1 求适合下列条件的椭圆的标准方程.
(1)焦点在y轴上,且经过两个点(0,2)和(1,0);
解 ∵椭圆的焦点在y轴上,
待定系数法
设标准方程
代入点求出a和b
注意判断标准方程的形式,看清焦点在哪里.
另解 ∵椭圆的焦点在y轴上,
且经过两个点(0,2)和(1,0)
∴a=2,b=1
求椭圆的标准方程
QIU TUO YUAN DE BIAO ZHUN FANG CHENG
(2)两个焦点的坐标分别是(0,-2),(0,2),并且椭圆经过点;
解 ∵椭圆的焦点在y轴上,
又c=2,∴b2=a2-c2=6,
待定系数法
设标准方程
代入点求出a和b
定义法
设标准方程
根据定义求出a和b
两者结合
求椭圆的标准方程
QIU TUO YUAN DE BIAO ZHUN FANG CHENG
(3)经过点A和点B ;
解 ①当椭圆的焦点在x轴上时,
待定系数法
设标准方程
代入点求出a和b
注意此时需要根据焦点的位置分类讨论
②当椭圆的焦点在y轴上时,
能否避免分类讨论?
求椭圆的标准方程
QIU TUO YUAN DE BIAO ZHUN FANG CHENG
(3)经过点A和点B ;
解
待定系数法
设标准方程
代入点求出a和b
当焦点位置不确定时,可设椭圆方程为:
+ n
(m≠n,m>0,n>0).
从而避免分类讨论.
动点的轨迹问题
DONG DIAN DE GUI JI WEN TI
例2 在圆上任取一点P,过点P作x轴的垂线段PD,D为垂足,求PD的中点M的轨迹方程;
解 设点M的坐标为,点P的坐标为,
则点D的坐标为.
∵M是线段PD的中点∴,.
又∵点 P 在圆上
∴
即
整理得
求动点的轨迹的思路
直接求解:根据条件写出x与y 的关系式并整理化简。
定义求解:动点运动的几何条件满足某种已知曲线的定义,待定系数法求出轨迹方程。
联系相关点:联系另一个动点在运动中所遵循的条件中去求解。
动点的轨迹问题
DONG DIAN DE GUI JI WEN TI
例3 设A ,B ,直线AM,BM相交于点M,且它们的斜率之积是,求点M的轨迹方程;
解 设点M的坐标为
求动点的轨迹的思路
直接求解:根据条件写出x与y 的关系式并整理化简。
定义求解:动点运动的几何条件满足某种已知曲线的定义,待定系数法求出轨迹方程。
联系相关点:联系另一个动点在运动中所遵循的条件中去求解。
∵ A∴直线AM的斜率是
同理,直线BM的斜率是
由题得
整理得
即点M的轨迹是除去和两点的椭圆
——练一练
解焦点三角形
JIE JIAO DIAN SAN JIAO XING
例4.1 经过椭圆上的右焦点F2作垂直于x轴的直线AB,交椭圆于A、B两点,F1是椭圆的左焦点,求AF1B的周长
椭圆上一点P与椭圆的两个焦点F1,F2构成的△PF1F2,称为焦点三角形。
|PF1|+|PF2|=2a
解三角形方法:
勾股定理
正弦、余弦定理等
解 由题意, AF1B的周长为:
++ AB
++ AF2 +BF2
+ AF2 ++BF2
又∵ 点A、B在椭圆上
+ = 5=20
即AF1B的周长为20.
追问 :若直线AB不垂直于x轴, AF1B的周长有什么变化?
原因是什么?
6
由此也可看出, AF1B的周长与直线AB是否垂直于x轴无关.
解焦点三角形
JIE JIAO DIAN SAN JIAO XING
例4.2 已知P为椭圆上一点,F1,F2是椭圆的焦点,∠F1PF2=60°,求F1PF2的面积.
∴|F1F2|=2c=6,
在△PF1F2中,|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|cos 60°,
即36=|PF1|2+|PF2|2-|PF1|·|PF2|. ①
即48=|PF1|2+|PF2|2+2|PF1|·|PF2|. ②
由①②得|PF1|·|PF2|=4.
椭圆上一点P与椭圆的两个焦点F1,F2构成的△PF1F2,称为焦点三角形。
|PF1|+|PF2|=2a
解三角形方法:
勾股定理
正弦、余弦定理等
解焦点三角形
JIE JIAO DIAN SAN JIAO XING
例4 已知P为椭圆上一点,F1,F2是椭圆的焦点,∠F1PF2=60°,求F1PF2的面积.
∴|F1F2|=2c=6,
在△PF1F2中,|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|cos 60°,
即36=|PF1|2+|PF2|2-|PF1|·|PF2|. ①
即48=|PF1|2+|PF2|2+2|PF1|·|PF2|. ②
由①②得|PF1|·|PF2|=4.
∠PF1F2=90°
在△PF1F2中,由勾股定理知|PF2|2=|PF1|2+|F1F2|2,
即|PF2|2=|PF1|2+36,
