青岛版数学八年级上册 2.4线段的垂直平分线第2课时线段的垂直平分线的尺规作图课件(共15张PPT)
文档属性
| 名称 | 青岛版数学八年级上册 2.4线段的垂直平分线第2课时线段的垂直平分线的尺规作图课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 486.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-11 00:00:00 | ||
图片预览



文档简介
(共15张PPT)
2.4 线段的垂直平分线
第2课时 线段的垂直平分线的尺规作图
学习目标
1.能用尺规完成基本作图:过一点作已知直线的垂线;
2.在尺规作图中,了解作图的道理,保留作图的痕迹;
3.利用过一点作已知直线的垂线解决实际问题,如解决最短路径问题等.
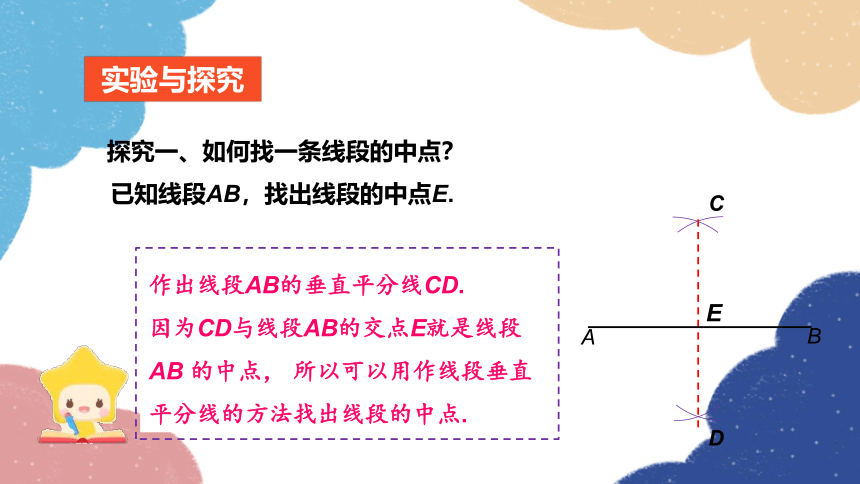
作出线段AB的垂直平分线CD.
因为CD与线段AB的交点E就是线段AB 的中点, 所以可以用作线段垂直平分线的方法找出线段的中点.
实验与探究
探究一、如何找一条线段的中点?
已知线段AB,找出线段的中点E.
A
B
C
D
E
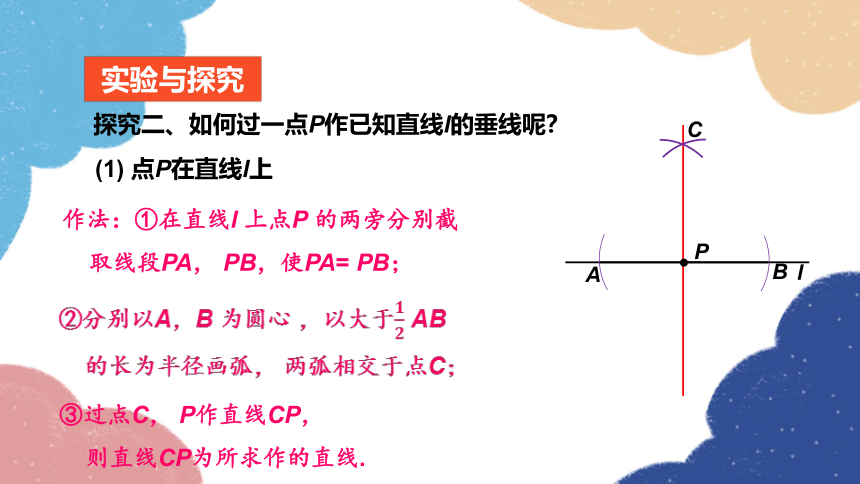
探究二、如何过一点P作已知直线l的垂线呢?
由于两点确定一条直线, 因此我们可以通过在已知直线上作线段的垂直平分线来找出垂线上的另一点,从而确定已知直线的垂线.
实验与探究
探究二、如何过一点P作已知直线l的垂线呢?
(1) 点P在直线l上
作法:①在直线l 上点P 的两旁分别截
取线段PA, PB,使PA= PB;
③过点C, P作直线CP,
则直线CP为所求作的直线.
P
l
A
B
C
实验与探究
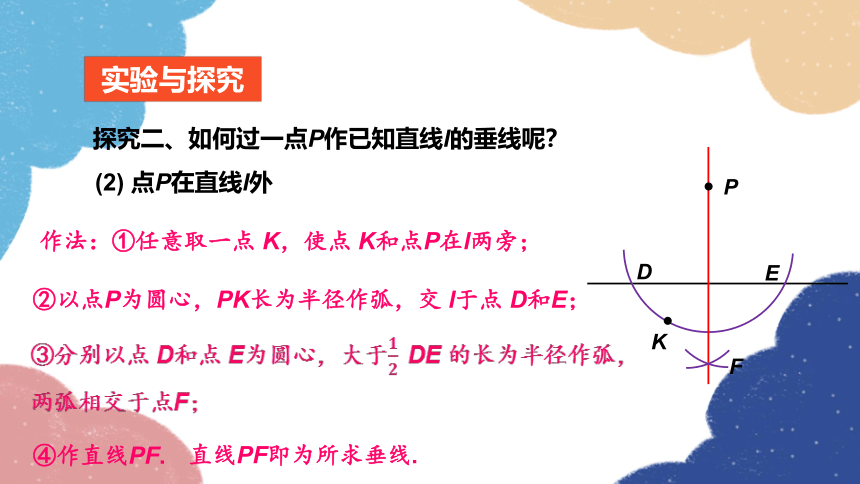
探究二、如何过一点P作已知直线l的垂线呢?
(2) 点P在直线l外
P
作法:①任意取一点 K,使点 K和点P在l两旁;
②以点P为圆心,PK长为半径作弧,交 l于点 D和E;
④作直线PF.
直线PF即为所求垂线.
K
D
E
实验与探究
F
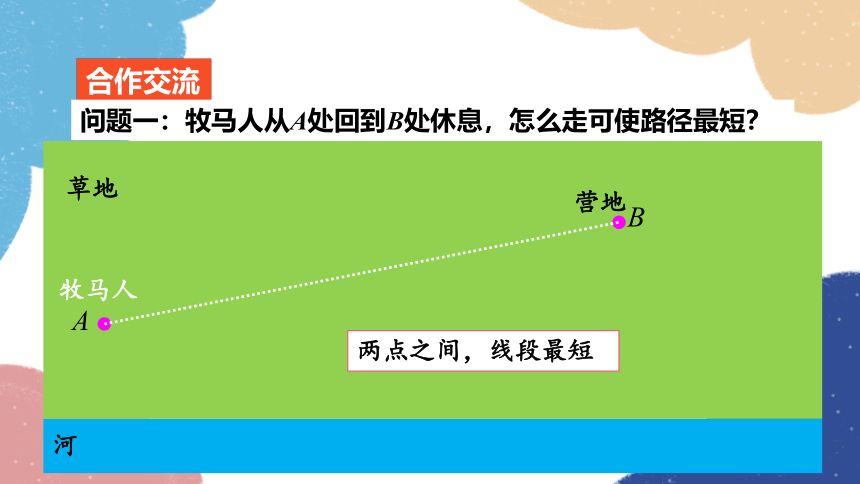
合作交流
草地
河
B
A
牧马人
营地
问题一:牧马人从A处回到B处休息,怎么走可使路径最短?
两点之间,线段最短
草地
河
B
A
牧马人
营地
l
D
问题二:牧马人从A处到河边 l 饮马,怎么走可使路径最短?
连接直线外一点与直线上各点的所有线段中,垂线段最短
“牧马饮水问题1”:
如图,牧马人从A地出发,先到河边l某处饮马,再穿过小河回到B处,牧马人到河边的什么地方饮马,可使所走的路径最短?请画出最短路径.
草地
河
A
B
l
C
C′
由“两点之间,线段最短”,
知AC+BC<AC′+BC′.
所以最短路径是AB.
当点A、B位于直线 l 的异侧时,连接AB,与直线 l 的交点,即为直线 l 上到A、B距离之和最短的点 .
AC+CB=AC+CB1=AB1,
AC1+C1B=AC1+C1B1>AB1.
所以最短路径是AC+BC.
草地
河
B
A
C1
C
B1
l
“牧马饮水问题2”:
如图,牧马人从A地出发,先到河边某处饮马,再回到B处,牧马人到河边的什么地方饮马,可使所走的路径最短?请画出最短路径.
当点A、B位于直线 l 的同侧时,作点B关于直线l的对称点B1,连接AB1,与直线l的交点,即为直线l上到A、B距离之和最短的点.
C
最短路径问题
A
B
(1)两点
(3)两点一线(异侧)
(4)两点一线(同侧)
(2)一点一线
A
l
A
B
l
A
l
B
C
C
B′
1.如图,A、B、C三个居民区的位置成三角形,现决定在这三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
A. AC,BC两边高线的交点处
B. AC,BC两边中线的交点处
C. AB,BC两边垂直平分线的交点处
D. ∠A,∠B两内角平分线的交点处
随堂训练
【解析】根据线段垂直平分线的性质,在线段垂直平分线上的点到线段两个端点的距离相等,可知超市应该建在AB,BC两边垂直平分线的交点处.
C
随堂训练
2.如图,四边形ABCD与四边形A′B′C′D′关于某直线对称,请你作出它们的对称轴.
A
B
C
D
A′
B′
C′
D′
E
F
解:如图,直线EF即为所求对称轴.
分析:连接任意两个对应点作其垂直平分线即是.
3.如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点,并说明理由.
·
·
C
A
B
a
作法:作点B关于直线 a 的对称点点C,连接AC交直线a于点D,则点D为建抽水站的位置.
随堂训练
·
D
3.如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点,并说明理由.
·
·
C
A
B
a
随堂训练
·
D
解:在 a 上另外任取一点E,
连接AE, CE,BE,BD,AD.
易得DB=DC,EB=EC,所以AD+DB=AD+DC=AC,AE+EB=AE+EC.在△ACE中,AE+EC>AC,
即 AE+EC>AD+DB ,
所以抽水站应建在河边的点D处.
E
·
2.4 线段的垂直平分线
第2课时 线段的垂直平分线的尺规作图
学习目标
1.能用尺规完成基本作图:过一点作已知直线的垂线;
2.在尺规作图中,了解作图的道理,保留作图的痕迹;
3.利用过一点作已知直线的垂线解决实际问题,如解决最短路径问题等.
作出线段AB的垂直平分线CD.
因为CD与线段AB的交点E就是线段AB 的中点, 所以可以用作线段垂直平分线的方法找出线段的中点.
实验与探究
探究一、如何找一条线段的中点?
已知线段AB,找出线段的中点E.
A
B
C
D
E
探究二、如何过一点P作已知直线l的垂线呢?
由于两点确定一条直线, 因此我们可以通过在已知直线上作线段的垂直平分线来找出垂线上的另一点,从而确定已知直线的垂线.
实验与探究
探究二、如何过一点P作已知直线l的垂线呢?
(1) 点P在直线l上
作法:①在直线l 上点P 的两旁分别截
取线段PA, PB,使PA= PB;
③过点C, P作直线CP,
则直线CP为所求作的直线.
P
l
A
B
C
实验与探究
探究二、如何过一点P作已知直线l的垂线呢?
(2) 点P在直线l外
P
作法:①任意取一点 K,使点 K和点P在l两旁;
②以点P为圆心,PK长为半径作弧,交 l于点 D和E;
④作直线PF.
直线PF即为所求垂线.
K
D
E
实验与探究
F
合作交流
草地
河
B
A
牧马人
营地
问题一:牧马人从A处回到B处休息,怎么走可使路径最短?
两点之间,线段最短
草地
河
B
A
牧马人
营地
l
D
问题二:牧马人从A处到河边 l 饮马,怎么走可使路径最短?
连接直线外一点与直线上各点的所有线段中,垂线段最短
“牧马饮水问题1”:
如图,牧马人从A地出发,先到河边l某处饮马,再穿过小河回到B处,牧马人到河边的什么地方饮马,可使所走的路径最短?请画出最短路径.
草地
河
A
B
l
C
C′
由“两点之间,线段最短”,
知AC+BC<AC′+BC′.
所以最短路径是AB.
当点A、B位于直线 l 的异侧时,连接AB,与直线 l 的交点,即为直线 l 上到A、B距离之和最短的点 .
AC+CB=AC+CB1=AB1,
AC1+C1B=AC1+C1B1>AB1.
所以最短路径是AC+BC.
草地
河
B
A
C1
C
B1
l
“牧马饮水问题2”:
如图,牧马人从A地出发,先到河边某处饮马,再回到B处,牧马人到河边的什么地方饮马,可使所走的路径最短?请画出最短路径.
当点A、B位于直线 l 的同侧时,作点B关于直线l的对称点B1,连接AB1,与直线l的交点,即为直线l上到A、B距离之和最短的点.
C
最短路径问题
A
B
(1)两点
(3)两点一线(异侧)
(4)两点一线(同侧)
(2)一点一线
A
l
A
B
l
A
l
B
C
C
B′
1.如图,A、B、C三个居民区的位置成三角形,现决定在这三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
A. AC,BC两边高线的交点处
B. AC,BC两边中线的交点处
C. AB,BC两边垂直平分线的交点处
D. ∠A,∠B两内角平分线的交点处
随堂训练
【解析】根据线段垂直平分线的性质,在线段垂直平分线上的点到线段两个端点的距离相等,可知超市应该建在AB,BC两边垂直平分线的交点处.
C
随堂训练
2.如图,四边形ABCD与四边形A′B′C′D′关于某直线对称,请你作出它们的对称轴.
A
B
C
D
A′
B′
C′
D′
E
F
解:如图,直线EF即为所求对称轴.
分析:连接任意两个对应点作其垂直平分线即是.
3.如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点,并说明理由.
·
·
C
A
B
a
作法:作点B关于直线 a 的对称点点C,连接AC交直线a于点D,则点D为建抽水站的位置.
随堂训练
·
D
3.如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点,并说明理由.
·
·
C
A
B
a
随堂训练
·
D
解:在 a 上另外任取一点E,
连接AE, CE,BE,BD,AD.
易得DB=DC,EB=EC,所以AD+DB=AD+DC=AC,AE+EB=AE+EC.在△ACE中,AE+EC>AC,
即 AE+EC>AD+DB ,
所以抽水站应建在河边的点D处.
E
·
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
