人教版数学八年级上册 11.1.2 三角形的高、中线与角平分线 课件(共25张PPT)
文档属性
| 名称 | 人教版数学八年级上册 11.1.2 三角形的高、中线与角平分线 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-11 16:26:33 | ||
图片预览




文档简介
(共25张PPT)
11.1.2 三角形的高、中线、角平分线
11.1与三角形有关的线段
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
在与三角形有关的线段中,除了它的三边外,还有它的高、中线和角平分线,这节课我们来学习三角形的高、中线和角平分线的意义、作法和发现的规律性结论.
讲授新知
贰
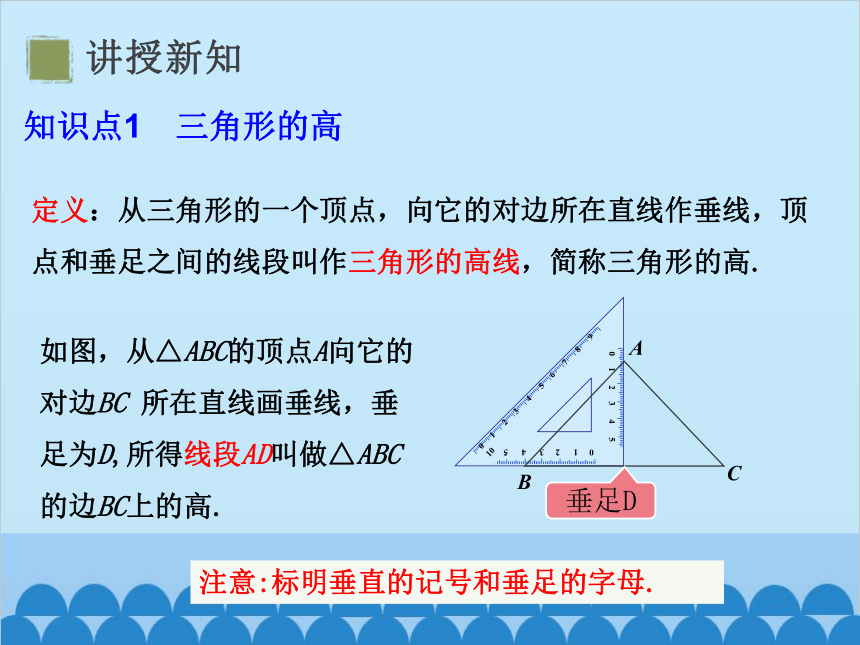
定义:从三角形的一个顶点,向它的对边所在直线作垂线,顶点和垂足之间的线段叫作三角形的高线,简称三角形的高.
如图,从△ABC的顶点A向它的对边BC 所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高.
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
A
B
C
垂足D
注意:标明垂直的记号和垂足的字母.
知识点1 三角形的高
讲授新知
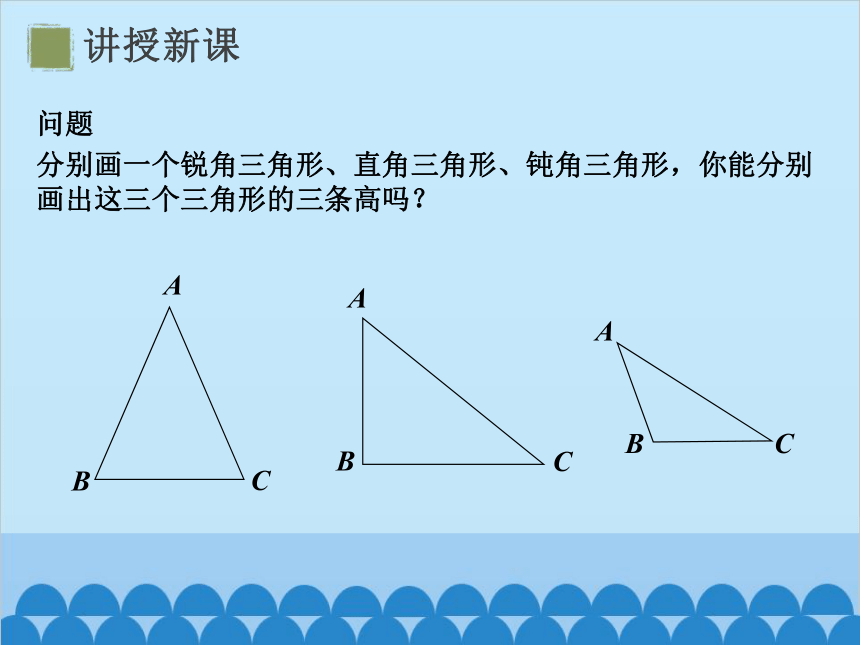
问题
分别画一个锐角三角形、直角三角形、钝角三角形,你能分别画出这三个三角形的三条高吗?
A
C
B
A
C
B
A
C
B
讲授新课
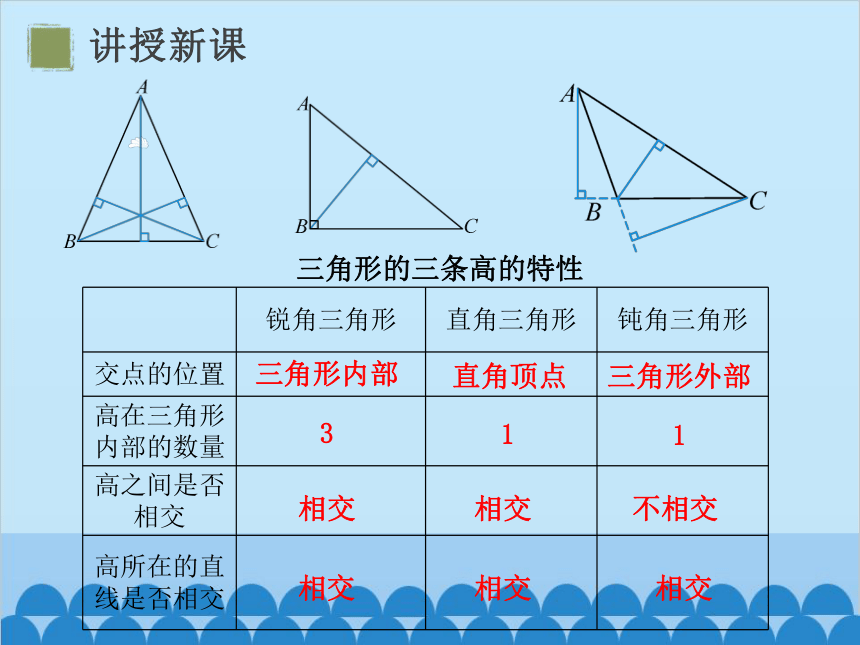
三角形的三条高的特性
锐角三角形 直角三角形 钝角三角形
交点的位置
高在三角形内部的数量
高之间是否相交
高所在的直线是否相交
三角形内部
直角顶点
三角形外部
3
1
1
相交
相交
不相交
相交
相交
相交
讲授新课
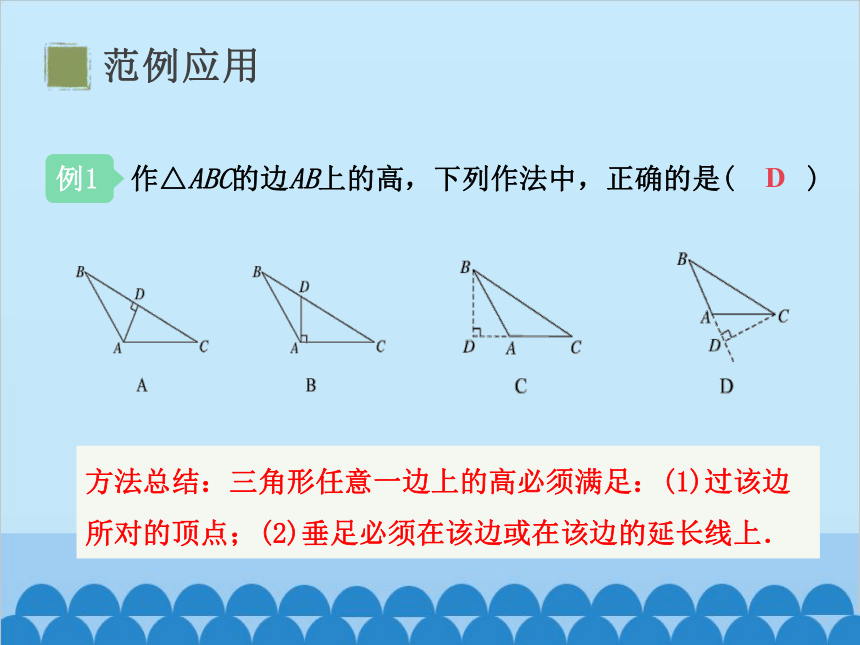
作△ABC的边AB上的高,下列作法中,正确的是( )
D
方法总结:三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
范例应用
例1
定义:连接三角形的一个顶点和它所对的中点的线段叫做三角形的中线.如图所示,AD是△ABC的边BC上的中线.
问题1:由三角形的中线能得到什么结论?
中线
中点
知识点2 三角形的中线
讲授新知
问题2:你能分别画出锐角三角形、直角三角形、钝角三角形的三条中线吗?观察它们中线的交点你会发现什么规律?
发现:三角形的三条中线交于三角形内部一点.这一点我们称为三角形的重心.
讲授新知
E
A
B
C
D
也就是说:三角形的任意一条中线把这个三角形分成了两个面积相等的三角形。
想一想:三角形的中线分成的两个三角形有什么关系
讲授新课
总结:三角形中线的特点
①任何三角形都有三条中线,并且都在三角形的内部,交与一点;
②三角形的中线是一条线段;
③三角形的任意一条中线把这个三角形分成了两个面积相等的三角形.
讲授新课
如图所示,AD为△ABC的中线,BE为三角形ABD中线,
(1)在△BED中作BD边上的高EF;
(2)若△ABC的面积为60,BD=5,求EF的长。
范例应用
例2
解:(1)
范例应用
三角形的三条角平分线相交于一点,交点在三角形的内部.
A
B
F
E
D
O
C
3.三角形的角平分线
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
因为AD是△ABC的角平分线
温馨提示:角的平分线是一条射线,三角形的角平分线是一条线段
讲授新课
例3
在△ABC中,已知∠A = 50°, BE , CF分别是∠ABC,∠ACB的平分线,相交于点P.∠ABP = 21°,求∠BCP的度数.
范例应用
当堂训练
叁
1.如图所示,在△ABC中, ∠1=∠2,G为AD中点,延长BG交 AC于E,F为AB上一点,CF交AD于H,判断下列说法的正误.
(1)AD是△ABE的角平分线( )
(2)BE是△ABD边AD上的中线( )
(3)BE是△ABC边AC上的中线( )
⌒
⌒
A
B
C
D
E
1
2
F
G
H
×
×
分析:
(1)AD线段不在△ABE内部,所以不是其角平分线
(2)BE 线段不在△ABD内部,所以不是其中线
(3)AE≠CE,所以BE不是△ABC边AC上的中线
×
当堂训练
B
当堂训练
D
3.如图所示,在等腰三角形ABC中,AB=AC,一腰上的中线BD 将这个等腰三角形的周长分成12 和6 两部分, 求这个等腰三角形的腰长及底边长.
解:设AB = AC = 2x,则AD = CD = x.
(1)当AB+AD = 12,BC+CD = 6 时,有2x+x = 12,
所以x = 4,2x = 8. 所以AB = AC = 8,BC = 6-4 = 2.
(2)当BC+CD = 12,AB+AD = 6 时,有2x+x = 6,
解得x = 2,所以2x = 4.
所以AB = AC = 4,BC = 12-2 = 10.
因为4+4<10,所以此时不能构成三角形.
综上所述,等腰三角形ABC 的腰长为8,底边长为2.
当堂训练
课堂小结
肆
课堂小结
三角形重要线段
三角形的三条角平分线交于三角形内部一点,这一点我们称为三角形的内心
直角三角形:三条高交于直角顶点
锐角三角形:三条高交于在三角形的内部一点
钝角三角形:三条高所在直线交于三角形外部一点
高
中线
三角形的三条中线交于三角形内部一点,这一点我们称为三角形的重心
一边上的中线把原三角形分成两个面积相等的三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
课后作业
基础题:1.课后练习 第 1,2题,P8页3,4题;
提高题:2.请学有余力的同学P8页8,9题.
谢
谢
11.1.2 三角形的高、中线、角平分线
11.1与三角形有关的线段
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
在与三角形有关的线段中,除了它的三边外,还有它的高、中线和角平分线,这节课我们来学习三角形的高、中线和角平分线的意义、作法和发现的规律性结论.
讲授新知
贰
定义:从三角形的一个顶点,向它的对边所在直线作垂线,顶点和垂足之间的线段叫作三角形的高线,简称三角形的高.
如图,从△ABC的顶点A向它的对边BC 所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高.
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
A
B
C
垂足D
注意:标明垂直的记号和垂足的字母.
知识点1 三角形的高
讲授新知
问题
分别画一个锐角三角形、直角三角形、钝角三角形,你能分别画出这三个三角形的三条高吗?
A
C
B
A
C
B
A
C
B
讲授新课
三角形的三条高的特性
锐角三角形 直角三角形 钝角三角形
交点的位置
高在三角形内部的数量
高之间是否相交
高所在的直线是否相交
三角形内部
直角顶点
三角形外部
3
1
1
相交
相交
不相交
相交
相交
相交
讲授新课
作△ABC的边AB上的高,下列作法中,正确的是( )
D
方法总结:三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
范例应用
例1
定义:连接三角形的一个顶点和它所对的中点的线段叫做三角形的中线.如图所示,AD是△ABC的边BC上的中线.
问题1:由三角形的中线能得到什么结论?
中线
中点
知识点2 三角形的中线
讲授新知
问题2:你能分别画出锐角三角形、直角三角形、钝角三角形的三条中线吗?观察它们中线的交点你会发现什么规律?
发现:三角形的三条中线交于三角形内部一点.这一点我们称为三角形的重心.
讲授新知
E
A
B
C
D
也就是说:三角形的任意一条中线把这个三角形分成了两个面积相等的三角形。
想一想:三角形的中线分成的两个三角形有什么关系
讲授新课
总结:三角形中线的特点
①任何三角形都有三条中线,并且都在三角形的内部,交与一点;
②三角形的中线是一条线段;
③三角形的任意一条中线把这个三角形分成了两个面积相等的三角形.
讲授新课
如图所示,AD为△ABC的中线,BE为三角形ABD中线,
(1)在△BED中作BD边上的高EF;
(2)若△ABC的面积为60,BD=5,求EF的长。
范例应用
例2
解:(1)
范例应用
三角形的三条角平分线相交于一点,交点在三角形的内部.
A
B
F
E
D
O
C
3.三角形的角平分线
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
因为AD是△ABC的角平分线
温馨提示:角的平分线是一条射线,三角形的角平分线是一条线段
讲授新课
例3
在△ABC中,已知∠A = 50°, BE , CF分别是∠ABC,∠ACB的平分线,相交于点P.∠ABP = 21°,求∠BCP的度数.
范例应用
当堂训练
叁
1.如图所示,在△ABC中, ∠1=∠2,G为AD中点,延长BG交 AC于E,F为AB上一点,CF交AD于H,判断下列说法的正误.
(1)AD是△ABE的角平分线( )
(2)BE是△ABD边AD上的中线( )
(3)BE是△ABC边AC上的中线( )
⌒
⌒
A
B
C
D
E
1
2
F
G
H
×
×
分析:
(1)AD线段不在△ABE内部,所以不是其角平分线
(2)BE 线段不在△ABD内部,所以不是其中线
(3)AE≠CE,所以BE不是△ABC边AC上的中线
×
当堂训练
B
当堂训练
D
3.如图所示,在等腰三角形ABC中,AB=AC,一腰上的中线BD 将这个等腰三角形的周长分成12 和6 两部分, 求这个等腰三角形的腰长及底边长.
解:设AB = AC = 2x,则AD = CD = x.
(1)当AB+AD = 12,BC+CD = 6 时,有2x+x = 12,
所以x = 4,2x = 8. 所以AB = AC = 8,BC = 6-4 = 2.
(2)当BC+CD = 12,AB+AD = 6 时,有2x+x = 6,
解得x = 2,所以2x = 4.
所以AB = AC = 4,BC = 12-2 = 10.
因为4+4<10,所以此时不能构成三角形.
综上所述,等腰三角形ABC 的腰长为8,底边长为2.
当堂训练
课堂小结
肆
课堂小结
三角形重要线段
三角形的三条角平分线交于三角形内部一点,这一点我们称为三角形的内心
直角三角形:三条高交于直角顶点
锐角三角形:三条高交于在三角形的内部一点
钝角三角形:三条高所在直线交于三角形外部一点
高
中线
三角形的三条中线交于三角形内部一点,这一点我们称为三角形的重心
一边上的中线把原三角形分成两个面积相等的三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
课后作业
基础题:1.课后练习 第 1,2题,P8页3,4题;
提高题:2.请学有余力的同学P8页8,9题.
谢
谢
