高中物理粵教版(2019)选择性必修第二册 第二章 电磁感应_电磁感应单元复习课课件(共36张PPT)
文档属性
| 名称 | 高中物理粵教版(2019)选择性必修第二册 第二章 电磁感应_电磁感应单元复习课课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-08-11 10:09:56 | ||
图片预览




文档简介
(共36张PPT)
高二—粤教版—物理—第二单元
电磁感应单元复习课
基础知识回顾
一、电磁感应相关知识
(一)法拉第电磁感应定律
1.产生感应电流(电动势)的条件
2.感应电流(电动势)的“方向”
3.感生、动生电动势的大小
4.自感与互感现象的理解与应用
基础知识回顾
一、电磁感应相关知识
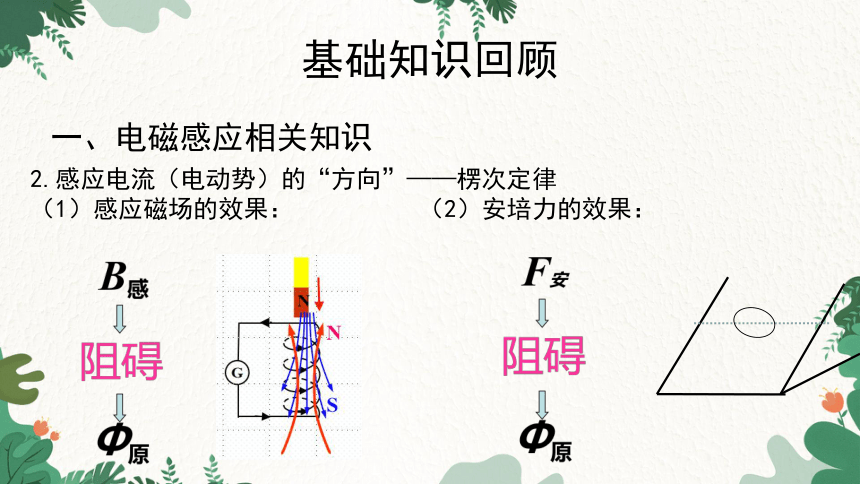
2.感应电流(电动势)的“方向”——楞次定律
(1)感应磁场的效果: (2)安培力的效果:
基础知识回顾
一、电磁感应相关知识
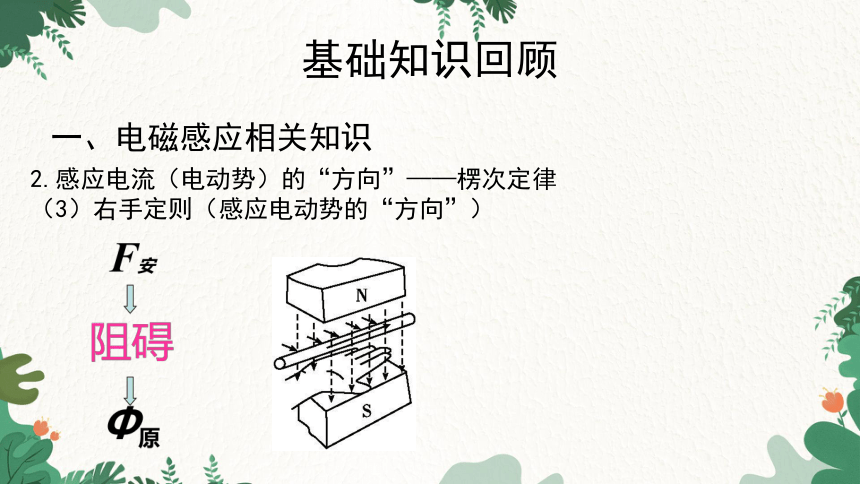
2.感应电流(电动势)的“方向”——楞次定律
(3)右手定则(感应电动势的“方向”)
基础知识回顾
一、电磁感应相关知识
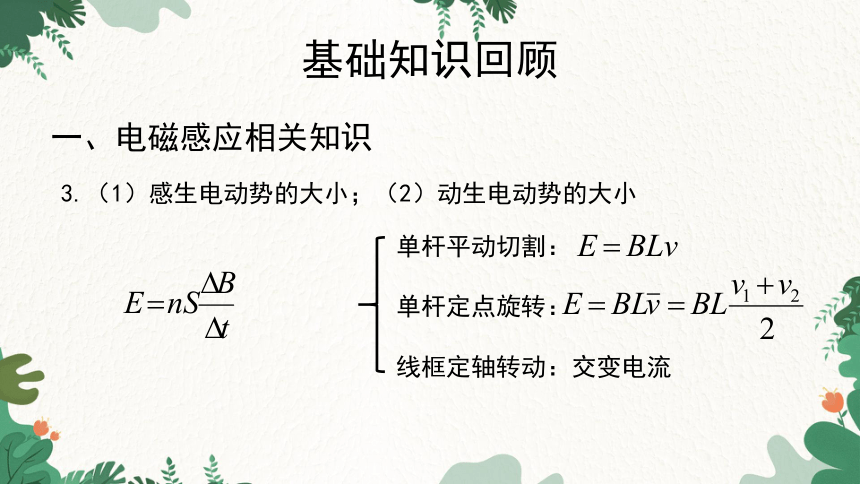
3.(1)感生电动势的大小;(2)动生电动势的大小
单杆平动切割:
单杆定点旋转:
线框定轴转动:交变电流
基础知识回顾
一、电磁感应相关知识
(一)法拉第电磁感应定律
1.产生感应电流(电动势)的条件
2.感应电流(电动势)的“方向”
3.感生、动生电动势的大小
4.自感与互感现象的理解与应用
(二)电磁感应定律的应用
1.电路问题分析
2.动力学问题分析
3.能量问题分析
二、电磁感应定律的应用——电路分析
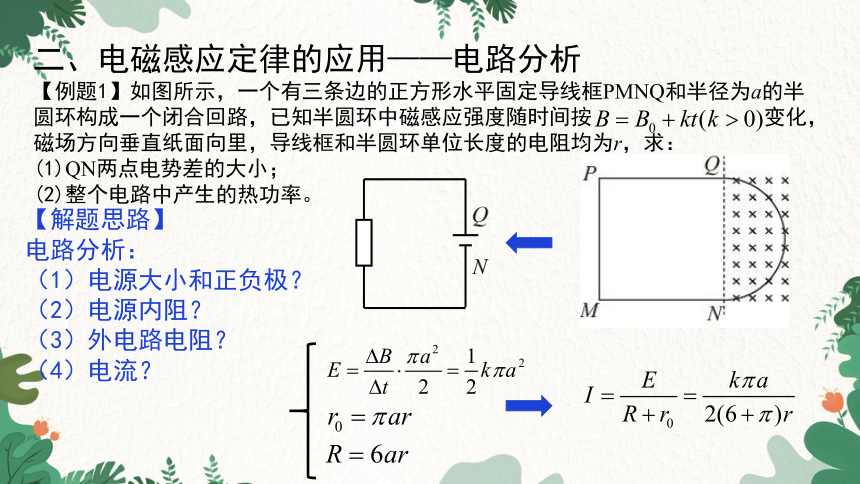
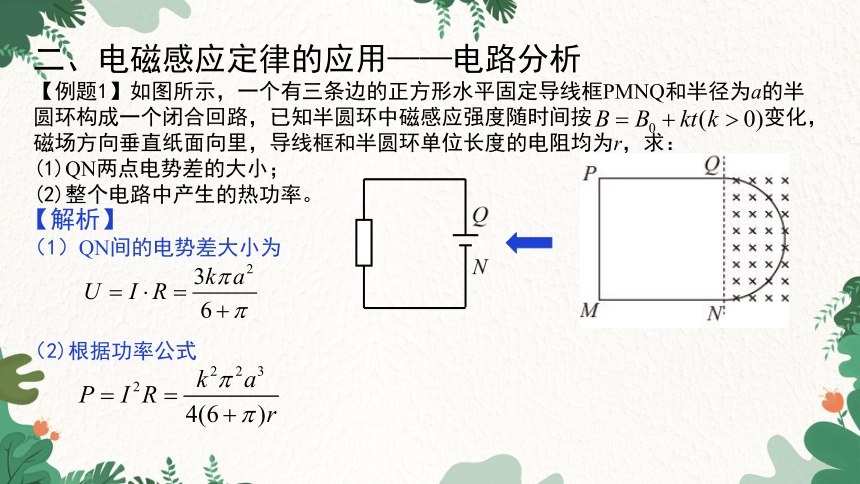
【例题1】如图所示,一个有三条边的正方形水平固定导线框PMNQ和半径为a的半圆环构成一个闭合回路,已知半圆环中磁感应强度随时间按 变化,磁场方向垂直纸面向里,导线框和半圆环单位长度的电阻均为r,求:
(1)QN两点电势差的大小;
(2)整个电路中产生的热功率。
二、电磁感应定律的应用——电路分析
【例题1】如图所示,一个有三条边的正方形水平固定导线框PMNQ和半径为a的半圆环构成一个闭合回路,已知半圆环中磁感应强度随时间按 变化,磁场方向垂直纸面向里,导线框和半圆环单位长度的电阻均为r,求:
(1)QN两点电势差的大小;
(2)整个电路中产生的热功率。
【解题思路】
电路分析:
(1)电源大小和正负极?
(2)电源内阻?
(3)外电路电阻?
(4)电流?
二、电磁感应定律的应用——电路分析
【例题1】如图所示,一个有三条边的正方形水平固定导线框PMNQ和半径为a的半圆环构成一个闭合回路,已知半圆环中磁感应强度随时间按 变化,磁场方向垂直纸面向里,导线框和半圆环单位长度的电阻均为r,求:
(1)QN两点电势差的大小;
(2)整个电路中产生的热功率。
【解析】
(1)QN间的电势差大小为
(2)根据功率公式
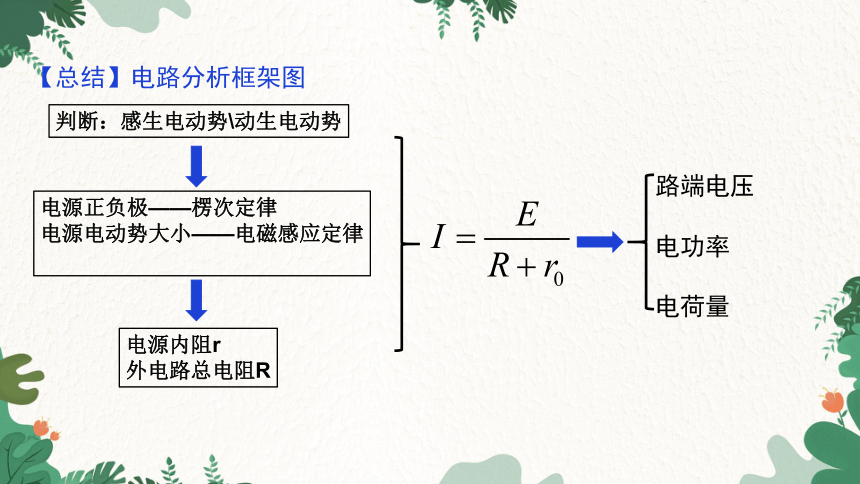
【总结】电路分析框架图
判断:感生电动势\动生电动势
电源正负极——楞次定律
电源电动势大小——电磁感应定律
电源内阻r
外电路总电阻R
路端电压
电功率
电荷量
三、电磁感应定律的应用——动力学问题分析
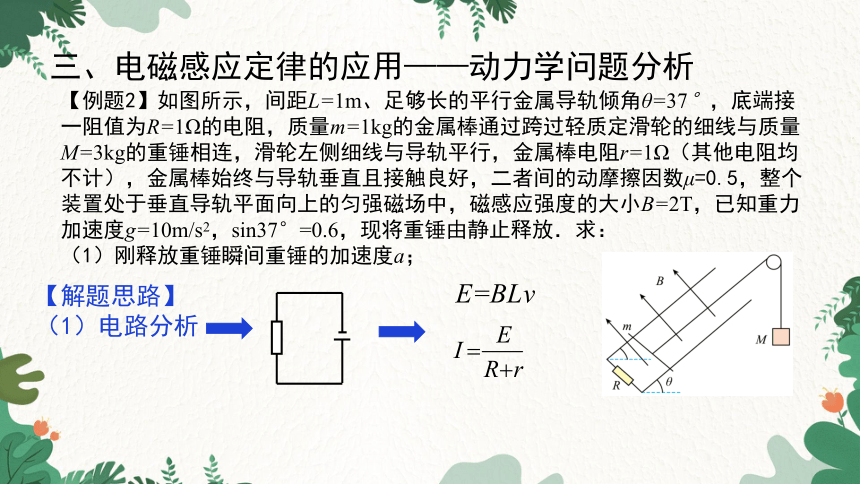
【例题2】如图所示,间距L=1m、足够长的平行金属导轨倾角θ=37°,底端接一阻值为R=1Ω的电阻,质量m=1kg的金属棒通过跨过轻质定滑轮的细线与质量M=3kg的重锤相连,滑轮左侧细线与导轨平行,金属棒电阻r=1Ω(其他电阻均不计),金属棒始终与导轨垂直且接触良好,二者间的动摩擦因数μ=0.5,整个装置处于垂直导轨平面向上的匀强磁场中,磁感应强度的大小B=2T,已知重力加速度g=10m/s2,sin37°=0.6,现将重锤由静止释放.求:
(1)刚释放重锤瞬间重锤的加速度a;
【解题思路】
(1)电路分析
三、电磁感应定律的应用——动力学问题分析
【例题2】如图所示,间距L=1m、足够长的平行金属导轨倾角θ=37°,底端接一阻值为R=1Ω的电阻,质量m=1kg的金属棒通过跨过轻质定滑轮的细线与质量M=3kg的重锤相连,滑轮左侧细线与导轨平行,金属棒电阻r=1Ω(其他电阻均不计),金属棒始终与导轨垂直且接触良好,二者间的动摩擦因数μ=0.5,整个装置处于垂直导轨平面向上的匀强磁场中,磁感应强度的大小B=2T,已知重力加速度g=10m/s2,sin37°=0.6,现将重锤由静止释放.求:
(1)刚释放重锤瞬间重锤的加速度a;
【解题思路】
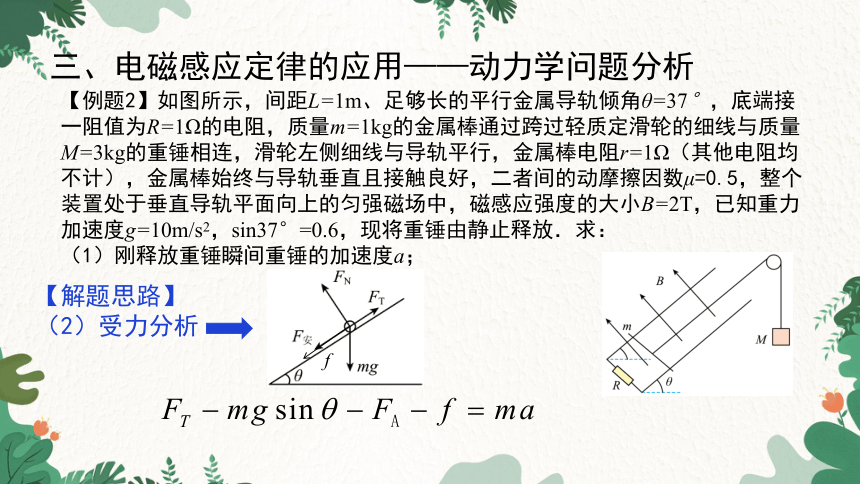
(2)受力分析
三、电磁感应定律的应用——动力学问题分析
【例题2】如图所示,间距L=1m、足够长的平行金属导轨倾角θ=37°,底端接一阻值为R=1Ω的电阻,质量m=1kg的金属棒通过跨过轻质定滑轮的细线与质量M=3kg的重锤相连,滑轮左侧细线与导轨平行,金属棒电阻r=1Ω(其他电阻均不计),金属棒始终与导轨垂直且接触良好,二者间的动摩擦因数μ=0.5,整个装置处于垂直导轨平面向上的匀强磁场中,磁感应强度的大小B=2T,已知重力加速度g=10m/s2,sin37°=0.6,现将重锤由静止释放.求:
(1)刚释放重锤瞬间重锤的加速度a;
【解析】
(1)刚释放重锤瞬间,以重锤为对象,根据牛顿第二定律得
以金属棒为对象,根据牛顿第二定律得
三、电磁感应定律的应用——动力学问题分析
【例题2】如图所示,间距L=1m、足够长的平行金属导轨倾角θ=37°,底端接一阻值为R=1Ω的电阻,质量m=1kg的金属棒通过跨过轻质定滑轮的细线与质量M=3kg的重锤相连,滑轮左侧细线与导轨平行,金属棒电阻r=1Ω(其他电阻均不计),金属棒始终与导轨垂直且接触良好,二者间的动摩擦因数μ=0.5,整个装置处于垂直导轨平面向上的匀强磁场中,磁感应强度的大小B=2T,已知重力加速度g=10m/s2,sin37°=0.6,现将重锤由静止释放.求:
(2)重锤的最大速度v;
【解题思路】
(3)运动分析
三、电磁感应定律的应用——动力学问题分析
【例题2】如图所示,间距L=1m、足够长的平行金属导轨倾角θ=37°,底端接一阻值为R=1Ω的电阻,质量m=1kg的金属棒通过跨过轻质定滑轮的细线与质量M=3kg的重锤相连,滑轮左侧细线与导轨平行,金属棒电阻r=1Ω(其他电阻均不计),金属棒始终与导轨垂直且接触良好,二者间的动摩擦因数μ=0.5,整个装置处于垂直导轨平面向上的匀强磁场中,磁感应强度的大小B=2T,已知重力加速度g=10m/s2,sin37°=0.6,现将重锤由静止释放.求:
(2)重锤的最大速度v;
【解题思路】
(3)运动分析
加速 F安 a a=0时,速度达到最大
【解析】以金属棒为对象,根据平衡量条件得
三、电磁感应定律的应用——动力学问题分析
四、电磁感应定律的应用——能量问题分析
【总结】
1、电磁感应中的能量转化
2、求解焦耳热Q的三种方法
三、电磁感应定律的应用——能量问题分析
【例题2】如图所示,间距L=1m、足够长的平行金属导轨倾角θ=37°,底端接一阻值为R=1Ω的电阻,质量m=1kg的金属棒通过跨过轻质定滑轮的细线与质量M=3kg的重锤相连,滑轮左侧细线与导轨平行,金属棒电阻r=1Ω(其他电阻均不计),金属棒始终与导轨垂直且接触良好,二者间的动摩擦因数μ=0.5,整个装置处于垂直导轨平面向上的匀强磁场中,磁感应强度的大小B=2T,已知重力加速度g=10m/s2,sin37°=0.6,现将重锤由静止释放.求:
(3)重锤下降h=20m时,其速度已经达到最大速度v,求这个过程中通过电阻R的电荷量q和电阻R上产生的焦耳热Q。
【解析】重锤下降h=20m时,其速度已经达到最大速度v,根据能量守恒定律得
电阻R上产生的焦耳热
三、电磁感应定律的应用——能量问题分析
【例题2】如图所示,间距L=1m、足够长的平行金属导轨倾角θ=37°,底端接一阻值为R=1Ω的电阻,质量m=1kg的金属棒通过跨过轻质定滑轮的细线与质量M=3kg的重锤相连,滑轮左侧细线与导轨平行,金属棒电阻r=1Ω(其他电阻均不计),金属棒始终与导轨垂直且接触良好,二者间的动摩擦因数μ=0.5,整个装置处于垂直导轨平面向上的匀强磁场中,磁感应强度的大小B=2T,已知重力加速度g=10m/s2,sin37°=0.6,现将重锤由静止释放.求:
(3)重锤下降h=20m时,其速度已经达到最大速度v,求这个过程中通过电阻R的电荷量q和电阻R上产生的焦耳热Q。
【解析】
重锤下降h=20m时,这个过程中通过电阻R的电荷量
三、电磁感应定律的应用——能量问题分析
【解题思路】
(1)电路分析+受力分析
cd棒动不动?
三、电磁感应定律的应用——能量问题分析
(1)若ab棒以ω0=12rad/s逆时针匀速转动,则流过ab棒的电流方向和ab棒两端的电压;
三、电磁感应定律的应用——能量问题分析
(1)若ab棒以ω0=12rad/s逆时针匀速转动,则流过ab棒的电流方向和ab棒两端的电压;
三、电磁感应定律的应用——能量问题分析
【解题思路】
(2)分类讨论/临界状态
三、电磁感应定律的应用——能量问题分析
(2)要使金属棒与导轨保持相对静止,则ab棒转动的角速度应满足什么条件?
三、电磁感应定律的应用——能量问题分析
(2)要使金属棒与导轨保持相对静止,则ab棒转动的角速度应满足什么条件?
三、电磁感应定律的应用——能量问题分析
三、电磁感应定律的应用——能量问题分析
(3)若ab棒以ω3=31rad/s顺时针匀速转动,当cd棒匀速时,cd棒的位移为x=16m,求:
①cd棒匀速的速度大小
②从静止到匀速,安培力对cd棒做的功
【解题思路】
电路分析:回路中有两个电源
受力分析:安培力随速度的增加而???
运动分析:cd杆的运动情况?
三、电磁感应定律的应用——能量问题分析
(3)若ab棒以ω3=31rad/s顺时针匀速转动,当cd棒匀速时,cd棒的位移为x=16m,求:
①cd棒匀速的速度大小
②从静止到匀速,安培力对cd棒做的功
三、电磁感应定律的应用——能量问题分析
(3)若ab棒以ω3=31rad/s顺时针匀速转动,当cd棒匀速时,cd棒的位移为x=16m,求:
①cd棒匀速的速度大小
②从静止到匀速,安培力对cd棒做的功
C
BD
【第7题】如图所示,一对平行的粗糙金属导轨固定于同一水平面上,导轨间距L=0.2m,左端接有阻值R=0.3Ω的电阻,右侧平滑连接一对弯曲的光滑轨道.水平导轨的整个区域内存在竖直向上的匀强磁场,磁感应强度大小B=1.0T,一根质量m=0.2kg,电阻r=0.1Ω的金属棒ab垂直放置于导轨上,在水平向右的恒力F作用下从静止开始运动,当金属棒通过位移x=9m时离开磁场,在离开磁场前已达到最大速度.当金属棒离开磁场时撤去外力F,接着金属棒沿弯曲轨道上升到最大高度h=0.8m处.已知金属棒与导轨间的动摩擦因数μ=0.1,导轨电阻不计,棒在运动过程中始终与轨道垂直且与轨道保持良好接触,取g=10m/s2,求:
(1)金属棒运动的最大速率v;
【第7题】如图所示,一对平行的粗糙金属导轨固定于同一水平面上,导轨间距L=0.2m,左端接有阻值R=0.3Ω的电阻,右侧平滑连接一对弯曲的光滑轨道.水平导轨的整个区域内存在竖直向上的匀强磁场,磁感应强度大小B=1.0T,一根质量m=0.2kg,电阻r=0.1Ω的金属棒ab垂直放置于导轨上,在水平向右的恒力F作用下从静止开始运动,当金属棒通过位移x=9m时离开磁场,在离开磁场前已达到最大速度.当金属棒离开磁场时撤去外力F,接着金属棒沿弯曲轨道上升到最大高度h=0.8m处.已知金属棒与导轨间的动摩擦因数μ=0.1,导轨电阻不计,棒在运动过程中始终与轨道垂直且与轨道保持良好接触,取g=10m/s2,求:
(3)金属棒在磁场区域运动过程中,电阻R上产生的焦耳热.
谢谢观看
高二—粤教版—物理—第二单元
电磁感应单元复习课
基础知识回顾
一、电磁感应相关知识
(一)法拉第电磁感应定律
1.产生感应电流(电动势)的条件
2.感应电流(电动势)的“方向”
3.感生、动生电动势的大小
4.自感与互感现象的理解与应用
基础知识回顾
一、电磁感应相关知识
2.感应电流(电动势)的“方向”——楞次定律
(1)感应磁场的效果: (2)安培力的效果:
基础知识回顾
一、电磁感应相关知识
2.感应电流(电动势)的“方向”——楞次定律
(3)右手定则(感应电动势的“方向”)
基础知识回顾
一、电磁感应相关知识
3.(1)感生电动势的大小;(2)动生电动势的大小
单杆平动切割:
单杆定点旋转:
线框定轴转动:交变电流
基础知识回顾
一、电磁感应相关知识
(一)法拉第电磁感应定律
1.产生感应电流(电动势)的条件
2.感应电流(电动势)的“方向”
3.感生、动生电动势的大小
4.自感与互感现象的理解与应用
(二)电磁感应定律的应用
1.电路问题分析
2.动力学问题分析
3.能量问题分析
二、电磁感应定律的应用——电路分析
【例题1】如图所示,一个有三条边的正方形水平固定导线框PMNQ和半径为a的半圆环构成一个闭合回路,已知半圆环中磁感应强度随时间按 变化,磁场方向垂直纸面向里,导线框和半圆环单位长度的电阻均为r,求:
(1)QN两点电势差的大小;
(2)整个电路中产生的热功率。
二、电磁感应定律的应用——电路分析
【例题1】如图所示,一个有三条边的正方形水平固定导线框PMNQ和半径为a的半圆环构成一个闭合回路,已知半圆环中磁感应强度随时间按 变化,磁场方向垂直纸面向里,导线框和半圆环单位长度的电阻均为r,求:
(1)QN两点电势差的大小;
(2)整个电路中产生的热功率。
【解题思路】
电路分析:
(1)电源大小和正负极?
(2)电源内阻?
(3)外电路电阻?
(4)电流?
二、电磁感应定律的应用——电路分析
【例题1】如图所示,一个有三条边的正方形水平固定导线框PMNQ和半径为a的半圆环构成一个闭合回路,已知半圆环中磁感应强度随时间按 变化,磁场方向垂直纸面向里,导线框和半圆环单位长度的电阻均为r,求:
(1)QN两点电势差的大小;
(2)整个电路中产生的热功率。
【解析】
(1)QN间的电势差大小为
(2)根据功率公式
【总结】电路分析框架图
判断:感生电动势\动生电动势
电源正负极——楞次定律
电源电动势大小——电磁感应定律
电源内阻r
外电路总电阻R
路端电压
电功率
电荷量
三、电磁感应定律的应用——动力学问题分析
【例题2】如图所示,间距L=1m、足够长的平行金属导轨倾角θ=37°,底端接一阻值为R=1Ω的电阻,质量m=1kg的金属棒通过跨过轻质定滑轮的细线与质量M=3kg的重锤相连,滑轮左侧细线与导轨平行,金属棒电阻r=1Ω(其他电阻均不计),金属棒始终与导轨垂直且接触良好,二者间的动摩擦因数μ=0.5,整个装置处于垂直导轨平面向上的匀强磁场中,磁感应强度的大小B=2T,已知重力加速度g=10m/s2,sin37°=0.6,现将重锤由静止释放.求:
(1)刚释放重锤瞬间重锤的加速度a;
【解题思路】
(1)电路分析
三、电磁感应定律的应用——动力学问题分析
【例题2】如图所示,间距L=1m、足够长的平行金属导轨倾角θ=37°,底端接一阻值为R=1Ω的电阻,质量m=1kg的金属棒通过跨过轻质定滑轮的细线与质量M=3kg的重锤相连,滑轮左侧细线与导轨平行,金属棒电阻r=1Ω(其他电阻均不计),金属棒始终与导轨垂直且接触良好,二者间的动摩擦因数μ=0.5,整个装置处于垂直导轨平面向上的匀强磁场中,磁感应强度的大小B=2T,已知重力加速度g=10m/s2,sin37°=0.6,现将重锤由静止释放.求:
(1)刚释放重锤瞬间重锤的加速度a;
【解题思路】
(2)受力分析
三、电磁感应定律的应用——动力学问题分析
【例题2】如图所示,间距L=1m、足够长的平行金属导轨倾角θ=37°,底端接一阻值为R=1Ω的电阻,质量m=1kg的金属棒通过跨过轻质定滑轮的细线与质量M=3kg的重锤相连,滑轮左侧细线与导轨平行,金属棒电阻r=1Ω(其他电阻均不计),金属棒始终与导轨垂直且接触良好,二者间的动摩擦因数μ=0.5,整个装置处于垂直导轨平面向上的匀强磁场中,磁感应强度的大小B=2T,已知重力加速度g=10m/s2,sin37°=0.6,现将重锤由静止释放.求:
(1)刚释放重锤瞬间重锤的加速度a;
【解析】
(1)刚释放重锤瞬间,以重锤为对象,根据牛顿第二定律得
以金属棒为对象,根据牛顿第二定律得
三、电磁感应定律的应用——动力学问题分析
【例题2】如图所示,间距L=1m、足够长的平行金属导轨倾角θ=37°,底端接一阻值为R=1Ω的电阻,质量m=1kg的金属棒通过跨过轻质定滑轮的细线与质量M=3kg的重锤相连,滑轮左侧细线与导轨平行,金属棒电阻r=1Ω(其他电阻均不计),金属棒始终与导轨垂直且接触良好,二者间的动摩擦因数μ=0.5,整个装置处于垂直导轨平面向上的匀强磁场中,磁感应强度的大小B=2T,已知重力加速度g=10m/s2,sin37°=0.6,现将重锤由静止释放.求:
(2)重锤的最大速度v;
【解题思路】
(3)运动分析
三、电磁感应定律的应用——动力学问题分析
【例题2】如图所示,间距L=1m、足够长的平行金属导轨倾角θ=37°,底端接一阻值为R=1Ω的电阻,质量m=1kg的金属棒通过跨过轻质定滑轮的细线与质量M=3kg的重锤相连,滑轮左侧细线与导轨平行,金属棒电阻r=1Ω(其他电阻均不计),金属棒始终与导轨垂直且接触良好,二者间的动摩擦因数μ=0.5,整个装置处于垂直导轨平面向上的匀强磁场中,磁感应强度的大小B=2T,已知重力加速度g=10m/s2,sin37°=0.6,现将重锤由静止释放.求:
(2)重锤的最大速度v;
【解题思路】
(3)运动分析
加速 F安 a a=0时,速度达到最大
【解析】以金属棒为对象,根据平衡量条件得
三、电磁感应定律的应用——动力学问题分析
四、电磁感应定律的应用——能量问题分析
【总结】
1、电磁感应中的能量转化
2、求解焦耳热Q的三种方法
三、电磁感应定律的应用——能量问题分析
【例题2】如图所示,间距L=1m、足够长的平行金属导轨倾角θ=37°,底端接一阻值为R=1Ω的电阻,质量m=1kg的金属棒通过跨过轻质定滑轮的细线与质量M=3kg的重锤相连,滑轮左侧细线与导轨平行,金属棒电阻r=1Ω(其他电阻均不计),金属棒始终与导轨垂直且接触良好,二者间的动摩擦因数μ=0.5,整个装置处于垂直导轨平面向上的匀强磁场中,磁感应强度的大小B=2T,已知重力加速度g=10m/s2,sin37°=0.6,现将重锤由静止释放.求:
(3)重锤下降h=20m时,其速度已经达到最大速度v,求这个过程中通过电阻R的电荷量q和电阻R上产生的焦耳热Q。
【解析】重锤下降h=20m时,其速度已经达到最大速度v,根据能量守恒定律得
电阻R上产生的焦耳热
三、电磁感应定律的应用——能量问题分析
【例题2】如图所示,间距L=1m、足够长的平行金属导轨倾角θ=37°,底端接一阻值为R=1Ω的电阻,质量m=1kg的金属棒通过跨过轻质定滑轮的细线与质量M=3kg的重锤相连,滑轮左侧细线与导轨平行,金属棒电阻r=1Ω(其他电阻均不计),金属棒始终与导轨垂直且接触良好,二者间的动摩擦因数μ=0.5,整个装置处于垂直导轨平面向上的匀强磁场中,磁感应强度的大小B=2T,已知重力加速度g=10m/s2,sin37°=0.6,现将重锤由静止释放.求:
(3)重锤下降h=20m时,其速度已经达到最大速度v,求这个过程中通过电阻R的电荷量q和电阻R上产生的焦耳热Q。
【解析】
重锤下降h=20m时,这个过程中通过电阻R的电荷量
三、电磁感应定律的应用——能量问题分析
【解题思路】
(1)电路分析+受力分析
cd棒动不动?
三、电磁感应定律的应用——能量问题分析
(1)若ab棒以ω0=12rad/s逆时针匀速转动,则流过ab棒的电流方向和ab棒两端的电压;
三、电磁感应定律的应用——能量问题分析
(1)若ab棒以ω0=12rad/s逆时针匀速转动,则流过ab棒的电流方向和ab棒两端的电压;
三、电磁感应定律的应用——能量问题分析
【解题思路】
(2)分类讨论/临界状态
三、电磁感应定律的应用——能量问题分析
(2)要使金属棒与导轨保持相对静止,则ab棒转动的角速度应满足什么条件?
三、电磁感应定律的应用——能量问题分析
(2)要使金属棒与导轨保持相对静止,则ab棒转动的角速度应满足什么条件?
三、电磁感应定律的应用——能量问题分析
三、电磁感应定律的应用——能量问题分析
(3)若ab棒以ω3=31rad/s顺时针匀速转动,当cd棒匀速时,cd棒的位移为x=16m,求:
①cd棒匀速的速度大小
②从静止到匀速,安培力对cd棒做的功
【解题思路】
电路分析:回路中有两个电源
受力分析:安培力随速度的增加而???
运动分析:cd杆的运动情况?
三、电磁感应定律的应用——能量问题分析
(3)若ab棒以ω3=31rad/s顺时针匀速转动,当cd棒匀速时,cd棒的位移为x=16m,求:
①cd棒匀速的速度大小
②从静止到匀速,安培力对cd棒做的功
三、电磁感应定律的应用——能量问题分析
(3)若ab棒以ω3=31rad/s顺时针匀速转动,当cd棒匀速时,cd棒的位移为x=16m,求:
①cd棒匀速的速度大小
②从静止到匀速,安培力对cd棒做的功
C
BD
【第7题】如图所示,一对平行的粗糙金属导轨固定于同一水平面上,导轨间距L=0.2m,左端接有阻值R=0.3Ω的电阻,右侧平滑连接一对弯曲的光滑轨道.水平导轨的整个区域内存在竖直向上的匀强磁场,磁感应强度大小B=1.0T,一根质量m=0.2kg,电阻r=0.1Ω的金属棒ab垂直放置于导轨上,在水平向右的恒力F作用下从静止开始运动,当金属棒通过位移x=9m时离开磁场,在离开磁场前已达到最大速度.当金属棒离开磁场时撤去外力F,接着金属棒沿弯曲轨道上升到最大高度h=0.8m处.已知金属棒与导轨间的动摩擦因数μ=0.1,导轨电阻不计,棒在运动过程中始终与轨道垂直且与轨道保持良好接触,取g=10m/s2,求:
(1)金属棒运动的最大速率v;
【第7题】如图所示,一对平行的粗糙金属导轨固定于同一水平面上,导轨间距L=0.2m,左端接有阻值R=0.3Ω的电阻,右侧平滑连接一对弯曲的光滑轨道.水平导轨的整个区域内存在竖直向上的匀强磁场,磁感应强度大小B=1.0T,一根质量m=0.2kg,电阻r=0.1Ω的金属棒ab垂直放置于导轨上,在水平向右的恒力F作用下从静止开始运动,当金属棒通过位移x=9m时离开磁场,在离开磁场前已达到最大速度.当金属棒离开磁场时撤去外力F,接着金属棒沿弯曲轨道上升到最大高度h=0.8m处.已知金属棒与导轨间的动摩擦因数μ=0.1,导轨电阻不计,棒在运动过程中始终与轨道垂直且与轨道保持良好接触,取g=10m/s2,求:
(3)金属棒在磁场区域运动过程中,电阻R上产生的焦耳热.
谢谢观看
同课章节目录
- 第一章 磁场
- 第一节 安培力
- 第二节 安培力的应用
- 第三节 洛伦兹力
- 第四节 洛伦兹力与现代技术
- 第二章 电磁感应
- 第一节 感应电流的方向
- 第二节 法拉第电磁感应定律
- 第三节 电磁感应定律的应用
- 第四节 互感和自感
- 第五节 涡流现象及其应用
- 第三章 交变电流
- 第一节 认识交变电流
- 第二节 描述交变电流的物理量
- 第三节 变压器
- 第四节 远距离输电
- 第四章 电磁震荡与电磁波
- 第一节 电磁振动
- 第二节 麦克斯韦电磁电磁场理论
- 第三节 电磁波的发射、传播和接收
- 第四节 电磁波谱
- 第五章 传感器
- 第一节 传感器及其工作原理
- 第二节 传感器的应用
- 第三节 用传感器制作自动控制装置
- 第四节 利用智能手机中的磁传感器研究磁现象
