八年级数学上分层优化堂堂清(4)11.2.1 第一课时 三角形的内角(含解析)
文档属性
| 名称 | 八年级数学上分层优化堂堂清(4)11.2.1 第一课时 三角形的内角(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 20:57:48 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
八年级数学上分层优化堂堂清
十一章 三角形
11.2与三角形有关的角
11.2.1 第一课时 三角形的内角
学习目标:
1.阐述并验证三角形内角和定理.
2.会用三角形内角和探索直角三角形性质与判定.
3.会运用三角形内角和定理进行计算.
老师对你说:
三角形内角和定理
◆1. 三角形内角的概念:三角形内角是三角形三边的夹角.每个三角形都有三个内角,且每个内角均大于0°且小于180°.
◆2.三角形内角和定理:三角形内角和是180°.
◆3.三角形内角和定理的证明:证明方法,不唯一,但其思路都是设法将三角形的三个内角移到一起,组合成一个平角.在转化中借助平行线.
◆4.三角形内角和定理的应用:主要用在求三角形中角的度数.
①直接根据两已知角求第三个角;
②依据三角形中角的关系,用代数方法求三个角;
基础提升 教材核心知识点精练
知识点1:三角形的内角和
【例1-1】在△ABC中,已知∠A+∠B=80°,∠C=2∠B,试求∠A,∠B和∠C的度数.
【例1-2】在△ABC中,∠A=80°,∠B是∠C的4倍,则∠B等于( )
A.85° B.80° C.75° D.70°
知识点2:三角形的内角和应用
【例2-1】如图,直线,三角尺的直角顶点在直线m上,且三角尺的直角被直线m平分,若,则下列结论错误的是( )
A. B. C. D.
【例2-2】如图,在中,,,平分,平分,则的大小是( )
A. B. C. D.
【例2-3】如图,将沿着平行于的直线折叠,得到,若,则的度数是( )
A. B. C. D.
能力强化提升训练
1.如图,在中,D、E、F三点分别在上,过点D的直线与线段相交于点M,已知
(1)说明:
(2)若,,,求的度数.
2.如图所示的几何图形,的度数为( )
A. B. C. D.
3.将两张三角形纸片如图摆放,量得∠1+∠2+∠3+∠4=220°,则∠5的度数为( )
A.30° B.40° C.45° D.50°
如图,在△ABC中,AD是△ABC的角平分线,BE⊥AC于点E,交DA的延长线于点F,若∠ABC=22°,∠C=34°,求∠F的度数.
堂堂清
填空题(每小题4分,共32分)
已知,在△ABC中,∠A=60°,∠C=80°,则∠B=( )
A.60° B.30° C.20° D.40°
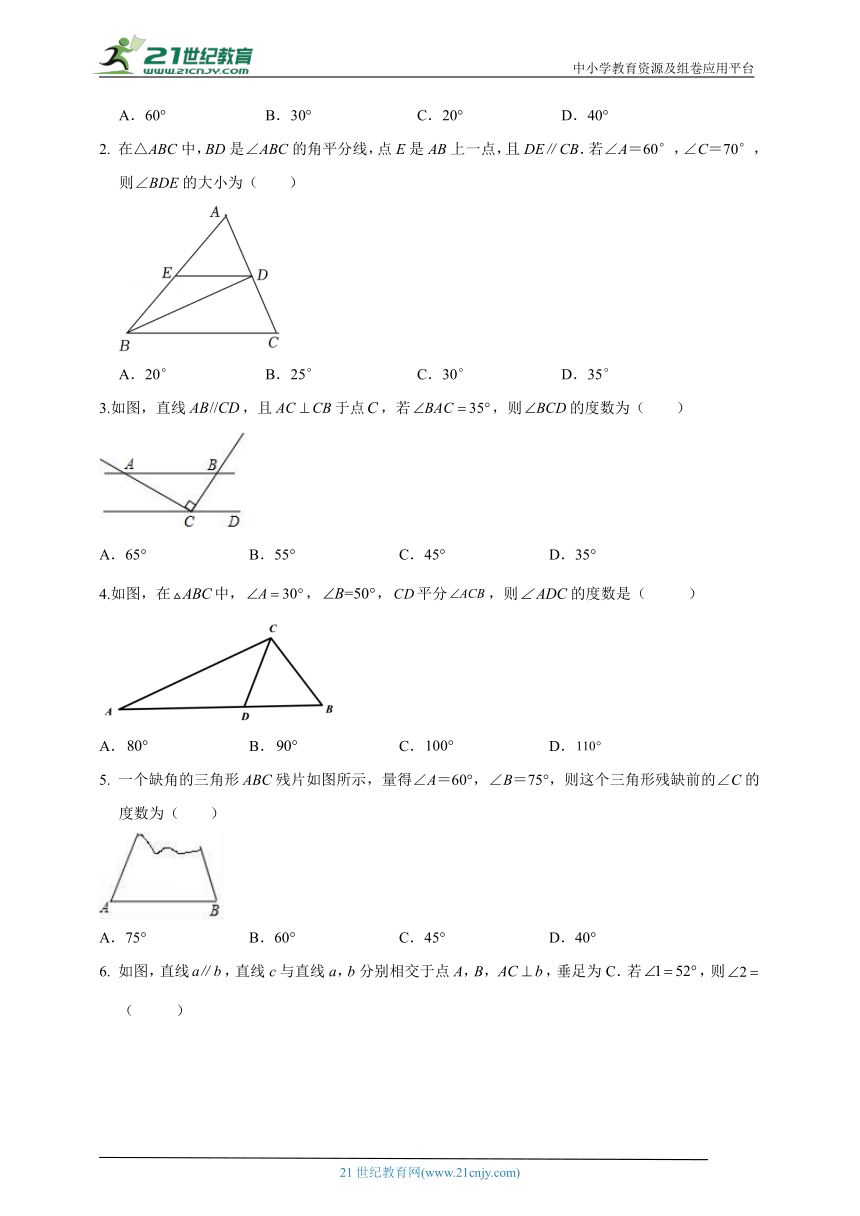
在△ABC中,BD是∠ABC的角平分线,点E是AB上一点,且DE∥CB.若∠A=60°,∠C=70°,则∠BDE的大小为( )
A.20° B.25° C.30° D.35°
3.如图,直线,且于点,若,则的度数为( )
A.65° B.55° C.45° D.35°
4.如图,在中,,,平分,则的度数是( )
A. B. C. D.
一个缺角的三角形ABC残片如图所示,量得∠A=60°,∠B=75°,则这个三角形残缺前的∠C的度数为( )
A.75° B.60° C.45° D.40°
如图,直线,直线c与直线a,b分别相交于点A,B,,垂足为C.若,则( )
A.52° B.45° C.38° D.26°
如图,李明同学在东西方向的滨海路A处,测得海中灯塔P在北偏东60°方向上,他向东走400米至B处,测得灯塔P在北偏东30°方向上,则从灯塔P观测A.B两处的视角∠P的度数是( )
A.30° B.32° C.35° D.40°
如图,把纸片沿折叠,当点A落在四边形内部时,则与之间有一种数量关系始终保持不变,这个关系是( )
A. B.
C. D.
填空题(每小题4分,共20分)
已知△ABC中,∠B=2∠A,∠C=∠A+40°,则∠A的度数为 .
10.将一副直角三角板按如图所示位置摆放(∠D=∠ECF=90°),点C在直角边BD上,点F在直角边AD上,若∠AFE=160°,则∠BCE=
11 .如图,在中,,平分,若,,则的度数为_____________.
12 .如图,△ABC中,∠A=54°,∠B=46°,点D、E分别在AB、AC上,连接DE并延长,交BC的延长线于F,若∠F=25°,则∠1的度数为 .
13 .如图,在中,沿折叠,点落在三角形所在的平面内的处, 若,,则_________.
解答题(共6小题,48分)
14.(6分)如图,△ABC中,∠ABC:∠C=5:7,∠C比∠A大10°,BD是△ABC的高,求∠A与∠CBD的度数.
15.(8分)如图,在中,是的平分线,高与相交于点.若,.求:
(1)的度数;
(2)的度数.
(8分)如图,点为的内角平分线与的交点,求证:.
17.(8分)如图,在△ABC中,AD是△ABC的角平分线,BE⊥AC于点E,交DA的延长线于点F,若∠ABC=22°,∠C=34°,求∠F的度数.
18.(8分)下面是证明三角形内角和定理的两种添加辅助线的方法,选择其中一种,完成证明.
三角形内角和定理:三角形三个内角和等于180°,已知:如图,,求证:
方法一证明:如图,过点A作 方法二证明:如图,过点C作
19 .(10分)如图1,已知线段AB、CD相交于点O,连接AC、BD.
(1)求证:∠A+∠C=∠B+∠D;
(2)如图2,∠CAB与∠BDC的平分线AP、DP相交于点P,求证:∠B+∠C=2∠P.
拓展培优*冲刺满分
1.在锐角△ABC中,AC边上的高所在直线和AB边上的高所在直线的交点为P,∠BPC=110°,求∠A的度数.
(2)如图1,AF和CE分别平分∠BAD和∠BCD,当点D在直线AC上时,且B、P、D三点共线,∠APC=100°,则∠B= .
(3)在(2)的基础上,当点D在直线AC外时,如图2:∠ADC=130°,∠APC=100°,求∠B的度数.
2.阅读材料:我们知道,探究不规则图形的角之间的关系时,可以通过辅助线将不规则图形转化为三角形,利用三角形内角和与内外角的关系获得结论.如图1,想要找到∠BDC与∠A+∠B+∠C之间的关系时,通过连接AD并延长到点E,得到△ABD和△ADC,进而求得∠BOC=∠A+∠B+∠C.请你应用材料中的方法,探究图2中∠A+∠B+∠C+∠D+∠E的度数.
3.我们将内角互为对顶角的两个三角形称为“对顶三角形”.例如,在图1中,△AOB的内角∠AOB与△COD的内角∠COD互为对顶角,则△AOB与∠COD为“对顶三角形”,根据三角形内角和定理知“对顶三角形”有如下性质:∠A+∠B=∠C+∠D.
性质理解:
(1)如图1,在“对顶三角形”△AOB与∠COD中,则∠AOB=70°,则∠C+∠D= 110 °.
性质应用:
(2)如图2,在△ABC中,AD、BE分别平分∠BAC和∠ABC,若∠C=60°,∠ADE比∠BED大6°,求∠BED的度数.
拓展提高:
(3)如图3,BE、CD是△ABC的角平分线,且∠BDC和∠BEC的平分线DP和EP相交于点P,设∠A=α,直接写出∠P的度数(用含α的式子表示∠P).
八年级数学上分层优化堂堂清
十一章 三角形
11.2与三角形有关的角
11.2.1 第一课时 三角形的内角(解析版)
学习目标:
1.阐述并验证三角形内角和定理.
2.会用三角形内角和探索直角三角形性质与判定.
3.会运用三角形内角和定理进行计算.
老师对你说:
三角形内角和定理
◆1. 三角形内角的概念:三角形内角是三角形三边的夹角.每个三角形都有三个内角,且每个内角均大于0°且小于180°.
◆2.三角形内角和定理:三角形内角和是180°.
◆3.三角形内角和定理的证明:证明方法,不唯一,但其思路都是设法将三角形的三个内角移到一起,组合成一个平角.在转化中借助平行线.
◆4.三角形内角和定理的应用:主要用在求三角形中角的度数.
①直接根据两已知角求第三个角;
②依据三角形中角的关系,用代数方法求三个角;
基础提升 教材核心知识点精练
知识点1:三角形的内角和
【例1-1】在△ABC中,已知∠A+∠B=80°,∠C=2∠B,试求∠A,∠B和∠C的度数.
【分析】题中给出两个条件:∠A+∠B=80°,∠C=2∠B,再根据三角形的内角和等于180°,即∠A+∠B+∠C=180°就可以求出∠A,∠B和∠C的度数.
【解析】
解:由∠A+∠B=80°及∠A+∠B+∠C=180°,
知∠C=100°.
又∵ ∠C=2∠B,
∴ ∠B=50°.
∴ ∠A=80°-∠B=80°-50°=30°.
【点评】解答本题的关键是利用隐含条件∠A+∠B+∠C=180°.本题可以设∠B=x,则∠A=80°-x,∠C=2x建立方程求解.
【例1-2】在△ABC中,∠A=80°,∠B是∠C的4倍,则∠B等于( )
A.85° B.80° C.75° D.70°
【分析】根据题意设∠C是x°,则∠B就是4x°,根据内角和为180°可列式为80°+x+4x=180°,解得x,即可求解.
【解答】解:设∠C是x°,则∠B就是4x°,根据题意可得:
80°+x+4x=180°,
解得:x=20,
20×4=80(度),
∴∠B=80°.
故选:B.
【点评】本题主要考查了三角形内角和定理,熟练使用三角形内角关系和三角形内角和定理是解决本题的关键.
知识点2:三角形的内角和应用
【例2-1】如图,直线,三角尺的直角顶点在直线m上,且三角尺的直角被直线m平分,若,则下列结论错误的是( )
A. B. C. D.
【答案】D
【分析】根据角平分线的定义求出∠6和∠7的度数,再利用平行线的性质以及三角形内角和求出∠3,∠8,∠2的度数,最后利用邻补角互补求出∠4和∠5的度数.
【详解】
首先根据三角尺的直角被直线m平分,
∴∠6=∠7=45°;
A、∵∠1=60°,∠6=45°,∴∠8=180°-∠1-∠6=180-60°-45°=75°,m∥n,∴∠2=∠8=75°结论正确,选项不合题意;
B、∵∠7=45°,m∥n,∴∠3=∠7=45°,结论正确,选项不合题意;
C、∵∠8=75°,∴∠4=180-∠8=180-75°=105°,结论正确,选项不合题意;
D、∵∠7=45°,∴∠5=180-∠7=180-45°=135°,结论错误,选项符合题意.
故选:D.
【点评】本题考查了角平分线的定义,平行线的性质,三角形内角和,邻补角互补,解答本题的关键是掌握平行线的性质:两直线平行,同位角相等,内错角相等,同旁内角互补.
【例2-2】如图,在中,,,平分,平分,则的大小是( )
A. B. C. D.
【答案】B
【分析】利用角平分线的定义先求得和的大小,然后利用三角形的内角和定理即可得到答案.
【详解】解:∵平分,平分,
∴,.
由三角形的内角和定理可知:
.
故选;B.
【点评】本题主要考查的是角平分线的定义、三角形的内角和定理,掌握角平分线的定义和三角形的内角和定理是解题的关键.
【例2-3】如图,将沿着平行于的直线折叠,得到,若,则的度数是( )
A. B. C. D.
【答案】B
【分析】根据题意可得,结合三角形内角和定理可得,最后根据平行线的性质求解即可.
【详解】解:由题意得,,
又∵,
∴,
∵,
∴,
故选:B.
【点评】本题考查了三角形内角和定理、平行线的性质和折叠的性质,灵活运用所学知识求解是解决本题的关键.
能力强化提升训练
1.如图,在中,D、E、F三点分别在上,过点D的直线与线段相交于点M,已知
(1)说明:
(2)若,,,求的度数.
【答案】(1)见解析
(2)
【思路点拨】(1)根据邻补角及题意得出,再由平行线的判定证明即可;
(2)根据平行线的判定和性质得出,再由三角形内角和定理求解即可.
【规范解答】(1)证明:∵,
∴
∴;
(2)∵,
∴,
∵
∴ ,
又∵,
∴.
∵,
∴,
∴.
∴.
【考点评析】题目主要考查平行线的判定和性质及三角形内角和定理,找准各角之间的关系是解题关键.
2.如图所示的几何图形,的度数为( )
A. B. C. D.
【答案】D
【思路点拨】连接,根据三角形的内角和等于,可得,再根据,即可求解.
【规范解答】解;如图,连接,则,
∵,
∴
,
故选:D.
【考点评析】本题考查三角形内角和定理、对顶角相等,整体思想的利用是解题的关键.
3.将两张三角形纸片如图摆放,量得∠1+∠2+∠3+∠4=220°,则∠5的度数为( )
A.30° B.40° C.45° D.50°
【分析】利用三角形的内角和定理计算即可.
【解答】解:如图,在△ADE中,
∵∠A+∠1+∠2=180°,
∴∠A=180°﹣(∠1+∠2),
在△BMN中,
∵∠B+∠3+∠4=180°,
∴∠B=180°﹣(∠3+∠4),
在△ABC中,
∵∠A+∠B+∠C=180°,
∴180°﹣(∠1+∠2)+180°﹣(∠3+∠4)+∠5=180°,
∴∠5=(∠1+∠2+∠3+∠4)﹣180°,
∵∠1+∠2+∠3+∠4=220°,
∴∠5=220°﹣180°=40°,
故选:B.
【点评】本题考查的三角形的内角和定理,找到每一个三角形的内角是解题的关键.
如图,在△ABC中,AD是△ABC的角平分线,BE⊥AC于点E,交DA的延长线于点F,若∠ABC=22°,∠C=34°,求∠F的度数.
【分析】根据三角形内角和定理以及角平分线的定义,和对顶角相等即可求出结果.
【解答】解:∵∠ABC=22°,∠C=34°,
∴∠BAC=180°﹣∠ABC﹣∠C=124°,
∵AD是△ABC的角平分线,
∴∠CAD62°,
∴∠FAE=62°,
∵BE⊥AC,
∴∠FEA=90°,
∴∠F=180°﹣∠FEA﹣∠FAE=28°.
【点评】本题考查了三角形内角和定理,角平分线的定义,熟练掌握三角形内角和定理是解题的关键.
堂堂清
填空题(每小题4分,共32分)
已知,在△ABC中,∠A=60°,∠C=80°,则∠B=( )
A.60° B.30° C.20° D.40°
【分析】直接根据三角形内角和定理进行解答即可.
【解答】解:∵在△ABC中,∠A=60°,∠C=80°,
∴∠B=180°﹣60°﹣80°=40°.
故选:D.
【点评】本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.
在△ABC中,BD是∠ABC的角平分线,点E是AB上一点,且DE∥CB.若∠A=60°,∠C=70°,则∠BDE的大小为( )
A.20° B.25° C.30° D.35°
【分析】根据三角形内角和定理求出∠ABC,再根据BD平分∠ABC,求出∠DBC,根据DE∥CB即可证明.
【解答】证明:∵∠A=60°,∠C=70°,
∴∠ABC=180°﹣∠A﹣∠C=180°﹣60°﹣70°=50°.
∵BD平分∠ABC,
∴∠DBC∠ABC=25°.
∵DE∥BC,
∴∠BDE=∠DBC=25°,
故选:B.
【点评】本题考查平行线的判定,解题关键是掌握三角形内角和定理,平行线的判定定理.
3.如图,直线,且于点,若,则的度数为( )
A.65° B.55° C.45° D.35°
【答案】B
【分析】根据三角形的内角和求得,再根据平行线的性质可得到的度数.
【详解】解:∵,,
∴,
∵,
∴,
故选:B.
【点评】本题考查三角形的内角和、平行线的性质,熟练运用平行线的性质定理是解题的关键.
4.如图,在中,,,平分,则的度数是( )
A. B. C. D.
【答案】C
【分析】在中,利用三角形内角和为求,再利用平分,求出的度数,再在利用三角形内角和定理即可求出的度数.
【详解】∵在中,,.
∴.
∵平分.
∴.
∴.
故选C.
【点评】本题考查了三角形的内角和和角平分线的性质,熟练应用性质是解决问题的关键.
一个缺角的三角形ABC残片如图所示,量得∠A=60°,∠B=75°,则这个三角形残缺前的∠C的度数为( )
A.75° B.60° C.45° D.40°
【答案】C
【分析】利用三角形内角和定理求解即可.
【详解】因为三角形内角和为180°,且∠A = 60°,∠B = 75°,所以∠C=180°–60°–75°=45°.
如图,直线,直线c与直线a,b分别相交于点A,B,,垂足为C.若,则( )
A.52° B.45° C.38° D.26°
【答案】C
【分析】根据平行线的性质可得∠ABC=52°,根据垂直定义可得∠ACB=90°,然后利用直角三角形的两个锐角互余,进行计算即可解答.
【详解】解:∵ab,
∴∠1=∠ABC=52°,
∵AC⊥b,
∴∠ACB=90°,
∴∠2=90°-∠ABC=38°,
故选:C.
【点评】本题考查了平行线的性质,垂线,熟练掌握平行线的性质是解题的关键.
如图,李明同学在东西方向的滨海路A处,测得海中灯塔P在北偏东60°方向上,他向东走400米至B处,测得灯塔P在北偏东30°方向上,则从灯塔P观测A.B两处的视角∠P的度数是( )
A.30° B.32° C.35° D.40°
【分析】在△ABP中,求出∠PAB、∠PBA的度数即可解决问题;
【解答】解:∵∠PAB=30°,∠ABP=120°,
∴∠APB=180°﹣∠PAB﹣∠ABP=30°.
故选:A.
【点评】本题考查了方向角,利用三角形的内角和是解题关键.
如图,把纸片沿折叠,当点A落在四边形内部时,则与之间有一种数量关系始终保持不变,这个关系是( )
A. B.
C. D.
【答案】A
【分析】根据折叠的性质和平角的定义先得到,再由三角形内角和定理得到,由此即可得到结论.
【详解】解:由折叠的性质可知 ,
∴,
由三角形内角和定理可知,
∴,
∴,
∴
故选:A.
【点评】本题主要考查了三角形内角和定理,折叠的性质,灵活运用所学知识是解题的关键.
填空题(每小题4分,共20分)
已知△ABC中,∠B=2∠A,∠C=∠A+40°,则∠A的度数为 .
【分析】利用题目条件结合三角形内角和180°即可列出关于∠A的方程,进而求出结果.
【解答】解:又三角形内角和定理可知:
∠A+∠B+∠C=180°,
∵∠B=2∠A,∠C=∠A+40°,
∴∠A+2∠A+∠A+40°=180°,
解得:∠A=35°.
故答案为:35°.
【点评】本题考查三角形内角和定理,属于基础题.
10.将一副直角三角板按如图所示位置摆放(∠D=∠ECF=90°),点C在直角边BD上,点F在直角边AD上,若∠AFE=160°,则∠BCE=
解:∵∠AFE=160°,
∴∠EFD=180°﹣∠AFE=20°,
∵∠CFE=45°,
∴∠DFC=∠CFE﹣∠EFD=25°,
∵∠D=∠ECF=90°,
∴∠DCF=180°﹣∠DFC﹣∠D=65°,
∴∠DCE=∠ECF﹣∠DCF=25°,
∴∠BCE=180°﹣∠DCE=155°.
故答案为:155°.
11 .如图,在中,,平分,若,,则的度数为_____________.
【答案】/度
【分析】先利用角平分线的定义求得,在利用直角三角形的两锐角互余求得,最后在中利用三角形的内角和即可求解.
【详解】解:∵平分,,,
∴,
∵,AD⊥BC,
∴,
∴在中,,
故答案为:.
【点评】本题考查了角平分线的定义,三角形的内角和定理,熟练掌握定义和定理是解题的关键.
12 .如图,△ABC中,∠A=54°,∠B=46°,点D、E分别在AB、AC上,连接DE并延长,交BC的延长线于F,若∠F=25°,则∠1的度数为 .
解:∵∠1=∠F+∠ECF,∠ECF=∠A+∠B,
∴∠1=∠F+∠A+∠B,
∵∠A=54°,∠B=46°,∠F=25°,
∴∠1=54°+46°+25°=125°.
故答案为:125°.
13 .如图,在中,沿折叠,点落在三角形所在的平面内的处, 若,,则_________.
【答案】/度
【分析】根据折叠的性质得出,,根据,得出,根据,即可求解.
【详解】解:∵沿折叠,点落在三角形所在的平面内的处,
∴,,
∵,
∴,
∴
∴
∴
∴,
故答案为:.
【点评】本题考查了折叠问题中的三角形内角和定理的应用,掌握折叠的性质以及三角形内角和定理是解题的关键.
解答题(共6小题,48分)
14.(6分)如图,△ABC中,∠ABC:∠C=5:7,∠C比∠A大10°,BD是△ABC的高,求∠A与∠CBD的度数.
【分析】由∠ABC:∠C=5:7,设∠ABC=5x,∠C=7x,然后由∠C比∠A大10°,可得:∠A=7x﹣10,然后根据三角形内角和定理可求∠A和∠C的度数,然后由BD是△ABC的高,可得:∠BDC=90°,然后根据三角形内角和定理可求∠CBD的度数.
【解答】解:∵∠ABC:∠C=5:7,
∴设∠ABC=5x,∠C=7x,
∵∠C比∠A大10°,
∴∠A=7x﹣10,
∵∠A+∠ABC+∠C=180°,
即:7x﹣10+5x+7x=180°,
解得:x=10,
∴∠C=7x=70°,∠A=7x﹣10=60°,
∵BD是△ABC的高,
∴∠BDC=90°,
∵∠BDC+∠C+∠CBD=180°,
∴∠CBD=20°.
【点评】此题考查了三角形内角和定理:三角形内角和为180°.解题的关键是:根据三角形内角和定理求出∠A和∠C的度数.
15.(8分)如图,在中,是的平分线,高与相交于点.若,.求:
(1)的度数;
(2)的度数.
【答案】(1)
(2)
【分析】(1)根据三角形的内角和定理即可求出答案.
(2)利用角平分线求出度数,在根据三角形内角和定理即可求出的度数,利用对顶角相等可求出的度数.
【详解】(1)解:,,
;
(2)解:,是的平分线,
,
高与相交于点,
,
,
,
(对顶角相等),
.
【点评】本题主要考查的知识点有三角形内角和定理、角平分线的定义和对顶角相等,解题过程中是否能熟练运用定理和性质是解题的关键.
(8分)如图,点为的内角平分线与的交点,求证:.
【答案】见解析
【分析】由角平分线的定义求得,,再利用三角形的内角和定理即可证明.
【详解】证明:、是角平分线,
,,
,
,
又,
.
【点评】本题考查了三角形内角和定理,角平分线的定义,熟练掌握三角形的内角和定理是解题的关键.
17.(8分)如图,在△ABC中,AD是△ABC的角平分线,BE⊥AC于点E,交DA的延长线于点F,若∠ABC=22°,∠C=34°,求∠F的度数.
【分析】根据三角形内角和定理以及角平分线的定义,和对顶角相等即可求出结果.
【解答】解:∵∠ABC=22°,∠C=34°,
∴∠BAC=180°﹣∠ABC﹣∠C=124°,
∵AD是△ABC的角平分线,
∴∠CAD62°,
∴∠FAE=62°,
∵BE⊥AC,
∴∠FEA=90°,
∴∠F=180°﹣∠FEA﹣∠FAE=28°.
【点评】本题考查了三角形内角和定理,角平分线的定义,熟练掌握三角形内角和定理是解题的关键.
18.(8分)下面是证明三角形内角和定理的两种添加辅助线的方法,选择其中一种,完成证明.
三角形内角和定理:三角形三个内角和等于180°,已知:如图,,求证:
方法一证明:如图,过点A作 方法二证明:如图,过点C作
【答案】答案见解析
【分析】选择方法一,过点作,依据平行线的性质,即可得到,,再根据平角的定义,即可得到三角形的内角和为.
【详解】证明:过点作,
则,. 两直线平行,内错角相等)
点,,在同一条直线上,
.(平角的定义)
.
即三角形的内角和为.
【点评】本题主要考查了平行线的性质以及三角形内角和定理的运用,熟练掌握平行线的性质是解题的关键.
19 .(10分)如图1,已知线段AB、CD相交于点O,连接AC、BD.
(1)求证:∠A+∠C=∠B+∠D;
(2)如图2,∠CAB与∠BDC的平分线AP、DP相交于点P,求证:∠B+∠C=2∠P.
【分析】(1)根据三角形的内角和即可得到结论;
(2)根据角平分线的定义和三角形的内角和解答即可.
【解答】证明:(1)在△AOC中,∠A+∠C=180°﹣∠AOC,
在△BOD中,∠B+∠D=180°﹣∠BOD,
∵∠AOC=∠BOD,
∴∠A+∠C=∠B+∠D;
(2)在AP、CD相交线中,有∠CAP+∠C=∠P+∠CDP,
在AB、DP相交线中,有∠B+∠BDP=∠P+∠BAP,
∴∠B+∠C+∠CAP+∠BDP=2∠P+∠CDP+∠BAP,
∵AP、DP分别平分∠CAB、∠BDC,
∴∠CAP=∠BAP,∠BDP=∠CDP,
∴∠B+∠C=2∠P.
【点评】本题考查了三角形内角和定理:三角形内角和是180°.也考查了角平分线的定义.
拓展培优*冲刺满分
1.在锐角△ABC中,AC边上的高所在直线和AB边上的高所在直线的交点为P,∠BPC=110°,求∠A的度数.
(2)如图1,AF和CE分别平分∠BAD和∠BCD,当点D在直线AC上时,且B、P、D三点共线,∠APC=100°,则∠B= .
(3)在(2)的基础上,当点D在直线AC外时,如图2:∠ADC=130°,∠APC=100°,求∠B的度数.
解:(1)如图1中,
∵AF,CE是高,
∴∠AFB=∠AEC=90°,
∵∠BPC=∠BEP+∠PBE,
∴∠PBE=110°﹣90°=20°,
∴∠A=90°﹣∠PBE=90°﹣20°=70°;
(2)∵∠APC=100°,
∴∠PAC+∠PCA=180°﹣100°=80°,
∵∠BAC=2∠PAC,∠BCA=2∠PCA,
∴∠BAC+∠BCA=160°,
∴∠B=180°﹣(∠BAC+∠BCA)=180°﹣160°=20°,
故答案为:20°;
(3)∵∠ADC=∠2+∠4+∠APC=130°,∠APC=∠1+∠3+∠B=100°,
∴∠2+∠4=30°,
∵∠1=∠2,∠3=∠4,
∴∠2+∠3=∠1+∠4=30°,
∴∠B=∠APC﹣(∠1+∠4)=70°.
2.阅读材料:我们知道,探究不规则图形的角之间的关系时,可以通过辅助线将不规则图形转化为三角形,利用三角形内角和与内外角的关系获得结论.如图1,想要找到∠BDC与∠A+∠B+∠C之间的关系时,通过连接AD并延长到点E,得到△ABD和△ADC,进而求得∠BOC=∠A+∠B+∠C.请你应用材料中的方法,探究图2中∠A+∠B+∠C+∠D+∠E的度数.
解:连接AF并延长至点M.
∴∠BAC=∠BAM+∠CAM.
∵∠BFM=∠B+∠BAM,∠CFM=∠C+∠CAM,
∴∠BFC=∠BFM+∠CFM=∠BAC+∠B+∠C.
∵∠D+∠E+∠EFD=180°,∠EFD=∠BFC,
∴∠D+∠E+∠BFC=180°.
∴∠A+∠B+∠C+∠D+∠E=180°.
3.我们将内角互为对顶角的两个三角形称为“对顶三角形”.例如,在图1中,△AOB的内角∠AOB与△COD的内角∠COD互为对顶角,则△AOB与∠COD为“对顶三角形”,根据三角形内角和定理知“对顶三角形”有如下性质:∠A+∠B=∠C+∠D.
性质理解:
(1)如图1,在“对顶三角形”△AOB与∠COD中,则∠AOB=70°,则∠C+∠D= 110 °.
性质应用:
(2)如图2,在△ABC中,AD、BE分别平分∠BAC和∠ABC,若∠C=60°,∠ADE比∠BED大6°,求∠BED的度数.
拓展提高:
(3)如图3,BE、CD是△ABC的角平分线,且∠BDC和∠BEC的平分线DP和EP相交于点P,设∠A=α,直接写出∠P的度数(用含α的式子表示∠P).
解:(1)在“对顶三角形”△AOB与∠COD中,则∠AOB=70°,
∴∠C+∠D=∠A+∠B=180°﹣∠AOB=110°,
故答案为:110;
(2)在△ABC中,∠C=60°,
∴∠BAC+∠ABC=120°.
∵AD、BE分别平分∠BAC和∠ABC,
∴,
∴∠ADE+∠BED=60°.
又∵∠ADE﹣∠BED=6°,
∴∠ADE=33°,∠BED=27°;
(3)在△ABC中,∠A=α,
∴∠ABC+∠ACB=180°﹣α.
∵BE、CD分别平分∠ABC和∠ACB,
∴,,
∴.
∵∠BDC和∠BEC的平分线DP和EP相交于点P,
∴,.
∵∠CEP+∠ACD=∠CDP+∠P,
∴==.
即
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
八年级数学上分层优化堂堂清
十一章 三角形
11.2与三角形有关的角
11.2.1 第一课时 三角形的内角
学习目标:
1.阐述并验证三角形内角和定理.
2.会用三角形内角和探索直角三角形性质与判定.
3.会运用三角形内角和定理进行计算.
老师对你说:
三角形内角和定理
◆1. 三角形内角的概念:三角形内角是三角形三边的夹角.每个三角形都有三个内角,且每个内角均大于0°且小于180°.
◆2.三角形内角和定理:三角形内角和是180°.
◆3.三角形内角和定理的证明:证明方法,不唯一,但其思路都是设法将三角形的三个内角移到一起,组合成一个平角.在转化中借助平行线.
◆4.三角形内角和定理的应用:主要用在求三角形中角的度数.
①直接根据两已知角求第三个角;
②依据三角形中角的关系,用代数方法求三个角;
基础提升 教材核心知识点精练
知识点1:三角形的内角和
【例1-1】在△ABC中,已知∠A+∠B=80°,∠C=2∠B,试求∠A,∠B和∠C的度数.
【例1-2】在△ABC中,∠A=80°,∠B是∠C的4倍,则∠B等于( )
A.85° B.80° C.75° D.70°
知识点2:三角形的内角和应用
【例2-1】如图,直线,三角尺的直角顶点在直线m上,且三角尺的直角被直线m平分,若,则下列结论错误的是( )
A. B. C. D.
【例2-2】如图,在中,,,平分,平分,则的大小是( )
A. B. C. D.
【例2-3】如图,将沿着平行于的直线折叠,得到,若,则的度数是( )
A. B. C. D.
能力强化提升训练
1.如图,在中,D、E、F三点分别在上,过点D的直线与线段相交于点M,已知
(1)说明:
(2)若,,,求的度数.
2.如图所示的几何图形,的度数为( )
A. B. C. D.
3.将两张三角形纸片如图摆放,量得∠1+∠2+∠3+∠4=220°,则∠5的度数为( )
A.30° B.40° C.45° D.50°
如图,在△ABC中,AD是△ABC的角平分线,BE⊥AC于点E,交DA的延长线于点F,若∠ABC=22°,∠C=34°,求∠F的度数.
堂堂清
填空题(每小题4分,共32分)
已知,在△ABC中,∠A=60°,∠C=80°,则∠B=( )
A.60° B.30° C.20° D.40°
在△ABC中,BD是∠ABC的角平分线,点E是AB上一点,且DE∥CB.若∠A=60°,∠C=70°,则∠BDE的大小为( )
A.20° B.25° C.30° D.35°
3.如图,直线,且于点,若,则的度数为( )
A.65° B.55° C.45° D.35°
4.如图,在中,,,平分,则的度数是( )
A. B. C. D.
一个缺角的三角形ABC残片如图所示,量得∠A=60°,∠B=75°,则这个三角形残缺前的∠C的度数为( )
A.75° B.60° C.45° D.40°
如图,直线,直线c与直线a,b分别相交于点A,B,,垂足为C.若,则( )
A.52° B.45° C.38° D.26°
如图,李明同学在东西方向的滨海路A处,测得海中灯塔P在北偏东60°方向上,他向东走400米至B处,测得灯塔P在北偏东30°方向上,则从灯塔P观测A.B两处的视角∠P的度数是( )
A.30° B.32° C.35° D.40°
如图,把纸片沿折叠,当点A落在四边形内部时,则与之间有一种数量关系始终保持不变,这个关系是( )
A. B.
C. D.
填空题(每小题4分,共20分)
已知△ABC中,∠B=2∠A,∠C=∠A+40°,则∠A的度数为 .
10.将一副直角三角板按如图所示位置摆放(∠D=∠ECF=90°),点C在直角边BD上,点F在直角边AD上,若∠AFE=160°,则∠BCE=
11 .如图,在中,,平分,若,,则的度数为_____________.
12 .如图,△ABC中,∠A=54°,∠B=46°,点D、E分别在AB、AC上,连接DE并延长,交BC的延长线于F,若∠F=25°,则∠1的度数为 .
13 .如图,在中,沿折叠,点落在三角形所在的平面内的处, 若,,则_________.
解答题(共6小题,48分)
14.(6分)如图,△ABC中,∠ABC:∠C=5:7,∠C比∠A大10°,BD是△ABC的高,求∠A与∠CBD的度数.
15.(8分)如图,在中,是的平分线,高与相交于点.若,.求:
(1)的度数;
(2)的度数.
(8分)如图,点为的内角平分线与的交点,求证:.
17.(8分)如图,在△ABC中,AD是△ABC的角平分线,BE⊥AC于点E,交DA的延长线于点F,若∠ABC=22°,∠C=34°,求∠F的度数.
18.(8分)下面是证明三角形内角和定理的两种添加辅助线的方法,选择其中一种,完成证明.
三角形内角和定理:三角形三个内角和等于180°,已知:如图,,求证:
方法一证明:如图,过点A作 方法二证明:如图,过点C作
19 .(10分)如图1,已知线段AB、CD相交于点O,连接AC、BD.
(1)求证:∠A+∠C=∠B+∠D;
(2)如图2,∠CAB与∠BDC的平分线AP、DP相交于点P,求证:∠B+∠C=2∠P.
拓展培优*冲刺满分
1.在锐角△ABC中,AC边上的高所在直线和AB边上的高所在直线的交点为P,∠BPC=110°,求∠A的度数.
(2)如图1,AF和CE分别平分∠BAD和∠BCD,当点D在直线AC上时,且B、P、D三点共线,∠APC=100°,则∠B= .
(3)在(2)的基础上,当点D在直线AC外时,如图2:∠ADC=130°,∠APC=100°,求∠B的度数.
2.阅读材料:我们知道,探究不规则图形的角之间的关系时,可以通过辅助线将不规则图形转化为三角形,利用三角形内角和与内外角的关系获得结论.如图1,想要找到∠BDC与∠A+∠B+∠C之间的关系时,通过连接AD并延长到点E,得到△ABD和△ADC,进而求得∠BOC=∠A+∠B+∠C.请你应用材料中的方法,探究图2中∠A+∠B+∠C+∠D+∠E的度数.
3.我们将内角互为对顶角的两个三角形称为“对顶三角形”.例如,在图1中,△AOB的内角∠AOB与△COD的内角∠COD互为对顶角,则△AOB与∠COD为“对顶三角形”,根据三角形内角和定理知“对顶三角形”有如下性质:∠A+∠B=∠C+∠D.
性质理解:
(1)如图1,在“对顶三角形”△AOB与∠COD中,则∠AOB=70°,则∠C+∠D= 110 °.
性质应用:
(2)如图2,在△ABC中,AD、BE分别平分∠BAC和∠ABC,若∠C=60°,∠ADE比∠BED大6°,求∠BED的度数.
拓展提高:
(3)如图3,BE、CD是△ABC的角平分线,且∠BDC和∠BEC的平分线DP和EP相交于点P,设∠A=α,直接写出∠P的度数(用含α的式子表示∠P).
八年级数学上分层优化堂堂清
十一章 三角形
11.2与三角形有关的角
11.2.1 第一课时 三角形的内角(解析版)
学习目标:
1.阐述并验证三角形内角和定理.
2.会用三角形内角和探索直角三角形性质与判定.
3.会运用三角形内角和定理进行计算.
老师对你说:
三角形内角和定理
◆1. 三角形内角的概念:三角形内角是三角形三边的夹角.每个三角形都有三个内角,且每个内角均大于0°且小于180°.
◆2.三角形内角和定理:三角形内角和是180°.
◆3.三角形内角和定理的证明:证明方法,不唯一,但其思路都是设法将三角形的三个内角移到一起,组合成一个平角.在转化中借助平行线.
◆4.三角形内角和定理的应用:主要用在求三角形中角的度数.
①直接根据两已知角求第三个角;
②依据三角形中角的关系,用代数方法求三个角;
基础提升 教材核心知识点精练
知识点1:三角形的内角和
【例1-1】在△ABC中,已知∠A+∠B=80°,∠C=2∠B,试求∠A,∠B和∠C的度数.
【分析】题中给出两个条件:∠A+∠B=80°,∠C=2∠B,再根据三角形的内角和等于180°,即∠A+∠B+∠C=180°就可以求出∠A,∠B和∠C的度数.
【解析】
解:由∠A+∠B=80°及∠A+∠B+∠C=180°,
知∠C=100°.
又∵ ∠C=2∠B,
∴ ∠B=50°.
∴ ∠A=80°-∠B=80°-50°=30°.
【点评】解答本题的关键是利用隐含条件∠A+∠B+∠C=180°.本题可以设∠B=x,则∠A=80°-x,∠C=2x建立方程求解.
【例1-2】在△ABC中,∠A=80°,∠B是∠C的4倍,则∠B等于( )
A.85° B.80° C.75° D.70°
【分析】根据题意设∠C是x°,则∠B就是4x°,根据内角和为180°可列式为80°+x+4x=180°,解得x,即可求解.
【解答】解:设∠C是x°,则∠B就是4x°,根据题意可得:
80°+x+4x=180°,
解得:x=20,
20×4=80(度),
∴∠B=80°.
故选:B.
【点评】本题主要考查了三角形内角和定理,熟练使用三角形内角关系和三角形内角和定理是解决本题的关键.
知识点2:三角形的内角和应用
【例2-1】如图,直线,三角尺的直角顶点在直线m上,且三角尺的直角被直线m平分,若,则下列结论错误的是( )
A. B. C. D.
【答案】D
【分析】根据角平分线的定义求出∠6和∠7的度数,再利用平行线的性质以及三角形内角和求出∠3,∠8,∠2的度数,最后利用邻补角互补求出∠4和∠5的度数.
【详解】
首先根据三角尺的直角被直线m平分,
∴∠6=∠7=45°;
A、∵∠1=60°,∠6=45°,∴∠8=180°-∠1-∠6=180-60°-45°=75°,m∥n,∴∠2=∠8=75°结论正确,选项不合题意;
B、∵∠7=45°,m∥n,∴∠3=∠7=45°,结论正确,选项不合题意;
C、∵∠8=75°,∴∠4=180-∠8=180-75°=105°,结论正确,选项不合题意;
D、∵∠7=45°,∴∠5=180-∠7=180-45°=135°,结论错误,选项符合题意.
故选:D.
【点评】本题考查了角平分线的定义,平行线的性质,三角形内角和,邻补角互补,解答本题的关键是掌握平行线的性质:两直线平行,同位角相等,内错角相等,同旁内角互补.
【例2-2】如图,在中,,,平分,平分,则的大小是( )
A. B. C. D.
【答案】B
【分析】利用角平分线的定义先求得和的大小,然后利用三角形的内角和定理即可得到答案.
【详解】解:∵平分,平分,
∴,.
由三角形的内角和定理可知:
.
故选;B.
【点评】本题主要考查的是角平分线的定义、三角形的内角和定理,掌握角平分线的定义和三角形的内角和定理是解题的关键.
【例2-3】如图,将沿着平行于的直线折叠,得到,若,则的度数是( )
A. B. C. D.
【答案】B
【分析】根据题意可得,结合三角形内角和定理可得,最后根据平行线的性质求解即可.
【详解】解:由题意得,,
又∵,
∴,
∵,
∴,
故选:B.
【点评】本题考查了三角形内角和定理、平行线的性质和折叠的性质,灵活运用所学知识求解是解决本题的关键.
能力强化提升训练
1.如图,在中,D、E、F三点分别在上,过点D的直线与线段相交于点M,已知
(1)说明:
(2)若,,,求的度数.
【答案】(1)见解析
(2)
【思路点拨】(1)根据邻补角及题意得出,再由平行线的判定证明即可;
(2)根据平行线的判定和性质得出,再由三角形内角和定理求解即可.
【规范解答】(1)证明:∵,
∴
∴;
(2)∵,
∴,
∵
∴ ,
又∵,
∴.
∵,
∴,
∴.
∴.
【考点评析】题目主要考查平行线的判定和性质及三角形内角和定理,找准各角之间的关系是解题关键.
2.如图所示的几何图形,的度数为( )
A. B. C. D.
【答案】D
【思路点拨】连接,根据三角形的内角和等于,可得,再根据,即可求解.
【规范解答】解;如图,连接,则,
∵,
∴
,
故选:D.
【考点评析】本题考查三角形内角和定理、对顶角相等,整体思想的利用是解题的关键.
3.将两张三角形纸片如图摆放,量得∠1+∠2+∠3+∠4=220°,则∠5的度数为( )
A.30° B.40° C.45° D.50°
【分析】利用三角形的内角和定理计算即可.
【解答】解:如图,在△ADE中,
∵∠A+∠1+∠2=180°,
∴∠A=180°﹣(∠1+∠2),
在△BMN中,
∵∠B+∠3+∠4=180°,
∴∠B=180°﹣(∠3+∠4),
在△ABC中,
∵∠A+∠B+∠C=180°,
∴180°﹣(∠1+∠2)+180°﹣(∠3+∠4)+∠5=180°,
∴∠5=(∠1+∠2+∠3+∠4)﹣180°,
∵∠1+∠2+∠3+∠4=220°,
∴∠5=220°﹣180°=40°,
故选:B.
【点评】本题考查的三角形的内角和定理,找到每一个三角形的内角是解题的关键.
如图,在△ABC中,AD是△ABC的角平分线,BE⊥AC于点E,交DA的延长线于点F,若∠ABC=22°,∠C=34°,求∠F的度数.
【分析】根据三角形内角和定理以及角平分线的定义,和对顶角相等即可求出结果.
【解答】解:∵∠ABC=22°,∠C=34°,
∴∠BAC=180°﹣∠ABC﹣∠C=124°,
∵AD是△ABC的角平分线,
∴∠CAD62°,
∴∠FAE=62°,
∵BE⊥AC,
∴∠FEA=90°,
∴∠F=180°﹣∠FEA﹣∠FAE=28°.
【点评】本题考查了三角形内角和定理,角平分线的定义,熟练掌握三角形内角和定理是解题的关键.
堂堂清
填空题(每小题4分,共32分)
已知,在△ABC中,∠A=60°,∠C=80°,则∠B=( )
A.60° B.30° C.20° D.40°
【分析】直接根据三角形内角和定理进行解答即可.
【解答】解:∵在△ABC中,∠A=60°,∠C=80°,
∴∠B=180°﹣60°﹣80°=40°.
故选:D.
【点评】本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.
在△ABC中,BD是∠ABC的角平分线,点E是AB上一点,且DE∥CB.若∠A=60°,∠C=70°,则∠BDE的大小为( )
A.20° B.25° C.30° D.35°
【分析】根据三角形内角和定理求出∠ABC,再根据BD平分∠ABC,求出∠DBC,根据DE∥CB即可证明.
【解答】证明:∵∠A=60°,∠C=70°,
∴∠ABC=180°﹣∠A﹣∠C=180°﹣60°﹣70°=50°.
∵BD平分∠ABC,
∴∠DBC∠ABC=25°.
∵DE∥BC,
∴∠BDE=∠DBC=25°,
故选:B.
【点评】本题考查平行线的判定,解题关键是掌握三角形内角和定理,平行线的判定定理.
3.如图,直线,且于点,若,则的度数为( )
A.65° B.55° C.45° D.35°
【答案】B
【分析】根据三角形的内角和求得,再根据平行线的性质可得到的度数.
【详解】解:∵,,
∴,
∵,
∴,
故选:B.
【点评】本题考查三角形的内角和、平行线的性质,熟练运用平行线的性质定理是解题的关键.
4.如图,在中,,,平分,则的度数是( )
A. B. C. D.
【答案】C
【分析】在中,利用三角形内角和为求,再利用平分,求出的度数,再在利用三角形内角和定理即可求出的度数.
【详解】∵在中,,.
∴.
∵平分.
∴.
∴.
故选C.
【点评】本题考查了三角形的内角和和角平分线的性质,熟练应用性质是解决问题的关键.
一个缺角的三角形ABC残片如图所示,量得∠A=60°,∠B=75°,则这个三角形残缺前的∠C的度数为( )
A.75° B.60° C.45° D.40°
【答案】C
【分析】利用三角形内角和定理求解即可.
【详解】因为三角形内角和为180°,且∠A = 60°,∠B = 75°,所以∠C=180°–60°–75°=45°.
如图,直线,直线c与直线a,b分别相交于点A,B,,垂足为C.若,则( )
A.52° B.45° C.38° D.26°
【答案】C
【分析】根据平行线的性质可得∠ABC=52°,根据垂直定义可得∠ACB=90°,然后利用直角三角形的两个锐角互余,进行计算即可解答.
【详解】解:∵ab,
∴∠1=∠ABC=52°,
∵AC⊥b,
∴∠ACB=90°,
∴∠2=90°-∠ABC=38°,
故选:C.
【点评】本题考查了平行线的性质,垂线,熟练掌握平行线的性质是解题的关键.
如图,李明同学在东西方向的滨海路A处,测得海中灯塔P在北偏东60°方向上,他向东走400米至B处,测得灯塔P在北偏东30°方向上,则从灯塔P观测A.B两处的视角∠P的度数是( )
A.30° B.32° C.35° D.40°
【分析】在△ABP中,求出∠PAB、∠PBA的度数即可解决问题;
【解答】解:∵∠PAB=30°,∠ABP=120°,
∴∠APB=180°﹣∠PAB﹣∠ABP=30°.
故选:A.
【点评】本题考查了方向角,利用三角形的内角和是解题关键.
如图,把纸片沿折叠,当点A落在四边形内部时,则与之间有一种数量关系始终保持不变,这个关系是( )
A. B.
C. D.
【答案】A
【分析】根据折叠的性质和平角的定义先得到,再由三角形内角和定理得到,由此即可得到结论.
【详解】解:由折叠的性质可知 ,
∴,
由三角形内角和定理可知,
∴,
∴,
∴
故选:A.
【点评】本题主要考查了三角形内角和定理,折叠的性质,灵活运用所学知识是解题的关键.
填空题(每小题4分,共20分)
已知△ABC中,∠B=2∠A,∠C=∠A+40°,则∠A的度数为 .
【分析】利用题目条件结合三角形内角和180°即可列出关于∠A的方程,进而求出结果.
【解答】解:又三角形内角和定理可知:
∠A+∠B+∠C=180°,
∵∠B=2∠A,∠C=∠A+40°,
∴∠A+2∠A+∠A+40°=180°,
解得:∠A=35°.
故答案为:35°.
【点评】本题考查三角形内角和定理,属于基础题.
10.将一副直角三角板按如图所示位置摆放(∠D=∠ECF=90°),点C在直角边BD上,点F在直角边AD上,若∠AFE=160°,则∠BCE=
解:∵∠AFE=160°,
∴∠EFD=180°﹣∠AFE=20°,
∵∠CFE=45°,
∴∠DFC=∠CFE﹣∠EFD=25°,
∵∠D=∠ECF=90°,
∴∠DCF=180°﹣∠DFC﹣∠D=65°,
∴∠DCE=∠ECF﹣∠DCF=25°,
∴∠BCE=180°﹣∠DCE=155°.
故答案为:155°.
11 .如图,在中,,平分,若,,则的度数为_____________.
【答案】/度
【分析】先利用角平分线的定义求得,在利用直角三角形的两锐角互余求得,最后在中利用三角形的内角和即可求解.
【详解】解:∵平分,,,
∴,
∵,AD⊥BC,
∴,
∴在中,,
故答案为:.
【点评】本题考查了角平分线的定义,三角形的内角和定理,熟练掌握定义和定理是解题的关键.
12 .如图,△ABC中,∠A=54°,∠B=46°,点D、E分别在AB、AC上,连接DE并延长,交BC的延长线于F,若∠F=25°,则∠1的度数为 .
解:∵∠1=∠F+∠ECF,∠ECF=∠A+∠B,
∴∠1=∠F+∠A+∠B,
∵∠A=54°,∠B=46°,∠F=25°,
∴∠1=54°+46°+25°=125°.
故答案为:125°.
13 .如图,在中,沿折叠,点落在三角形所在的平面内的处, 若,,则_________.
【答案】/度
【分析】根据折叠的性质得出,,根据,得出,根据,即可求解.
【详解】解:∵沿折叠,点落在三角形所在的平面内的处,
∴,,
∵,
∴,
∴
∴
∴
∴,
故答案为:.
【点评】本题考查了折叠问题中的三角形内角和定理的应用,掌握折叠的性质以及三角形内角和定理是解题的关键.
解答题(共6小题,48分)
14.(6分)如图,△ABC中,∠ABC:∠C=5:7,∠C比∠A大10°,BD是△ABC的高,求∠A与∠CBD的度数.
【分析】由∠ABC:∠C=5:7,设∠ABC=5x,∠C=7x,然后由∠C比∠A大10°,可得:∠A=7x﹣10,然后根据三角形内角和定理可求∠A和∠C的度数,然后由BD是△ABC的高,可得:∠BDC=90°,然后根据三角形内角和定理可求∠CBD的度数.
【解答】解:∵∠ABC:∠C=5:7,
∴设∠ABC=5x,∠C=7x,
∵∠C比∠A大10°,
∴∠A=7x﹣10,
∵∠A+∠ABC+∠C=180°,
即:7x﹣10+5x+7x=180°,
解得:x=10,
∴∠C=7x=70°,∠A=7x﹣10=60°,
∵BD是△ABC的高,
∴∠BDC=90°,
∵∠BDC+∠C+∠CBD=180°,
∴∠CBD=20°.
【点评】此题考查了三角形内角和定理:三角形内角和为180°.解题的关键是:根据三角形内角和定理求出∠A和∠C的度数.
15.(8分)如图,在中,是的平分线,高与相交于点.若,.求:
(1)的度数;
(2)的度数.
【答案】(1)
(2)
【分析】(1)根据三角形的内角和定理即可求出答案.
(2)利用角平分线求出度数,在根据三角形内角和定理即可求出的度数,利用对顶角相等可求出的度数.
【详解】(1)解:,,
;
(2)解:,是的平分线,
,
高与相交于点,
,
,
,
(对顶角相等),
.
【点评】本题主要考查的知识点有三角形内角和定理、角平分线的定义和对顶角相等,解题过程中是否能熟练运用定理和性质是解题的关键.
(8分)如图,点为的内角平分线与的交点,求证:.
【答案】见解析
【分析】由角平分线的定义求得,,再利用三角形的内角和定理即可证明.
【详解】证明:、是角平分线,
,,
,
,
又,
.
【点评】本题考查了三角形内角和定理,角平分线的定义,熟练掌握三角形的内角和定理是解题的关键.
17.(8分)如图,在△ABC中,AD是△ABC的角平分线,BE⊥AC于点E,交DA的延长线于点F,若∠ABC=22°,∠C=34°,求∠F的度数.
【分析】根据三角形内角和定理以及角平分线的定义,和对顶角相等即可求出结果.
【解答】解:∵∠ABC=22°,∠C=34°,
∴∠BAC=180°﹣∠ABC﹣∠C=124°,
∵AD是△ABC的角平分线,
∴∠CAD62°,
∴∠FAE=62°,
∵BE⊥AC,
∴∠FEA=90°,
∴∠F=180°﹣∠FEA﹣∠FAE=28°.
【点评】本题考查了三角形内角和定理,角平分线的定义,熟练掌握三角形内角和定理是解题的关键.
18.(8分)下面是证明三角形内角和定理的两种添加辅助线的方法,选择其中一种,完成证明.
三角形内角和定理:三角形三个内角和等于180°,已知:如图,,求证:
方法一证明:如图,过点A作 方法二证明:如图,过点C作
【答案】答案见解析
【分析】选择方法一,过点作,依据平行线的性质,即可得到,,再根据平角的定义,即可得到三角形的内角和为.
【详解】证明:过点作,
则,. 两直线平行,内错角相等)
点,,在同一条直线上,
.(平角的定义)
.
即三角形的内角和为.
【点评】本题主要考查了平行线的性质以及三角形内角和定理的运用,熟练掌握平行线的性质是解题的关键.
19 .(10分)如图1,已知线段AB、CD相交于点O,连接AC、BD.
(1)求证:∠A+∠C=∠B+∠D;
(2)如图2,∠CAB与∠BDC的平分线AP、DP相交于点P,求证:∠B+∠C=2∠P.
【分析】(1)根据三角形的内角和即可得到结论;
(2)根据角平分线的定义和三角形的内角和解答即可.
【解答】证明:(1)在△AOC中,∠A+∠C=180°﹣∠AOC,
在△BOD中,∠B+∠D=180°﹣∠BOD,
∵∠AOC=∠BOD,
∴∠A+∠C=∠B+∠D;
(2)在AP、CD相交线中,有∠CAP+∠C=∠P+∠CDP,
在AB、DP相交线中,有∠B+∠BDP=∠P+∠BAP,
∴∠B+∠C+∠CAP+∠BDP=2∠P+∠CDP+∠BAP,
∵AP、DP分别平分∠CAB、∠BDC,
∴∠CAP=∠BAP,∠BDP=∠CDP,
∴∠B+∠C=2∠P.
【点评】本题考查了三角形内角和定理:三角形内角和是180°.也考查了角平分线的定义.
拓展培优*冲刺满分
1.在锐角△ABC中,AC边上的高所在直线和AB边上的高所在直线的交点为P,∠BPC=110°,求∠A的度数.
(2)如图1,AF和CE分别平分∠BAD和∠BCD,当点D在直线AC上时,且B、P、D三点共线,∠APC=100°,则∠B= .
(3)在(2)的基础上,当点D在直线AC外时,如图2:∠ADC=130°,∠APC=100°,求∠B的度数.
解:(1)如图1中,
∵AF,CE是高,
∴∠AFB=∠AEC=90°,
∵∠BPC=∠BEP+∠PBE,
∴∠PBE=110°﹣90°=20°,
∴∠A=90°﹣∠PBE=90°﹣20°=70°;
(2)∵∠APC=100°,
∴∠PAC+∠PCA=180°﹣100°=80°,
∵∠BAC=2∠PAC,∠BCA=2∠PCA,
∴∠BAC+∠BCA=160°,
∴∠B=180°﹣(∠BAC+∠BCA)=180°﹣160°=20°,
故答案为:20°;
(3)∵∠ADC=∠2+∠4+∠APC=130°,∠APC=∠1+∠3+∠B=100°,
∴∠2+∠4=30°,
∵∠1=∠2,∠3=∠4,
∴∠2+∠3=∠1+∠4=30°,
∴∠B=∠APC﹣(∠1+∠4)=70°.
2.阅读材料:我们知道,探究不规则图形的角之间的关系时,可以通过辅助线将不规则图形转化为三角形,利用三角形内角和与内外角的关系获得结论.如图1,想要找到∠BDC与∠A+∠B+∠C之间的关系时,通过连接AD并延长到点E,得到△ABD和△ADC,进而求得∠BOC=∠A+∠B+∠C.请你应用材料中的方法,探究图2中∠A+∠B+∠C+∠D+∠E的度数.
解:连接AF并延长至点M.
∴∠BAC=∠BAM+∠CAM.
∵∠BFM=∠B+∠BAM,∠CFM=∠C+∠CAM,
∴∠BFC=∠BFM+∠CFM=∠BAC+∠B+∠C.
∵∠D+∠E+∠EFD=180°,∠EFD=∠BFC,
∴∠D+∠E+∠BFC=180°.
∴∠A+∠B+∠C+∠D+∠E=180°.
3.我们将内角互为对顶角的两个三角形称为“对顶三角形”.例如,在图1中,△AOB的内角∠AOB与△COD的内角∠COD互为对顶角,则△AOB与∠COD为“对顶三角形”,根据三角形内角和定理知“对顶三角形”有如下性质:∠A+∠B=∠C+∠D.
性质理解:
(1)如图1,在“对顶三角形”△AOB与∠COD中,则∠AOB=70°,则∠C+∠D= 110 °.
性质应用:
(2)如图2,在△ABC中,AD、BE分别平分∠BAC和∠ABC,若∠C=60°,∠ADE比∠BED大6°,求∠BED的度数.
拓展提高:
(3)如图3,BE、CD是△ABC的角平分线,且∠BDC和∠BEC的平分线DP和EP相交于点P,设∠A=α,直接写出∠P的度数(用含α的式子表示∠P).
解:(1)在“对顶三角形”△AOB与∠COD中,则∠AOB=70°,
∴∠C+∠D=∠A+∠B=180°﹣∠AOB=110°,
故答案为:110;
(2)在△ABC中,∠C=60°,
∴∠BAC+∠ABC=120°.
∵AD、BE分别平分∠BAC和∠ABC,
∴,
∴∠ADE+∠BED=60°.
又∵∠ADE﹣∠BED=6°,
∴∠ADE=33°,∠BED=27°;
(3)在△ABC中,∠A=α,
∴∠ABC+∠ACB=180°﹣α.
∵BE、CD分别平分∠ABC和∠ACB,
∴,,
∴.
∵∠BDC和∠BEC的平分线DP和EP相交于点P,
∴,.
∵∠CEP+∠ACD=∠CDP+∠P,
∴==.
即
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
