八年级数学上分层优化堂堂清(7)专题 与三角形角有关的几何模型(一)(含解析)
文档属性
| 名称 | 八年级数学上分层优化堂堂清(7)专题 与三角形角有关的几何模型(一)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 21:04:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
八年级数学上分层优化堂堂清
十一章 三角形
几何模型专题
与三角形角有关的几何模型(一)
模型一 角的“8”字模型
如图1-1所示,AC,BD相交于点O,连接AD,BC.
结论:(1)∠A+∠D=∠B+∠C.
(2)AD+BC BD+AC
图1-1
模型结论的推导:
(1)∵∠A+∠D+∠AOD=180°( ),
∠B+∠C+∠BOC=180°( ),
又∠AOD=∠BOC( ),
∴∠A+∠D=∠B+∠C.
AD①+②得:AD+BC模型的应用1:
1.如图1-2,∠A=43°,∠D=57°,∠C=37°,则∠B的度数为 .
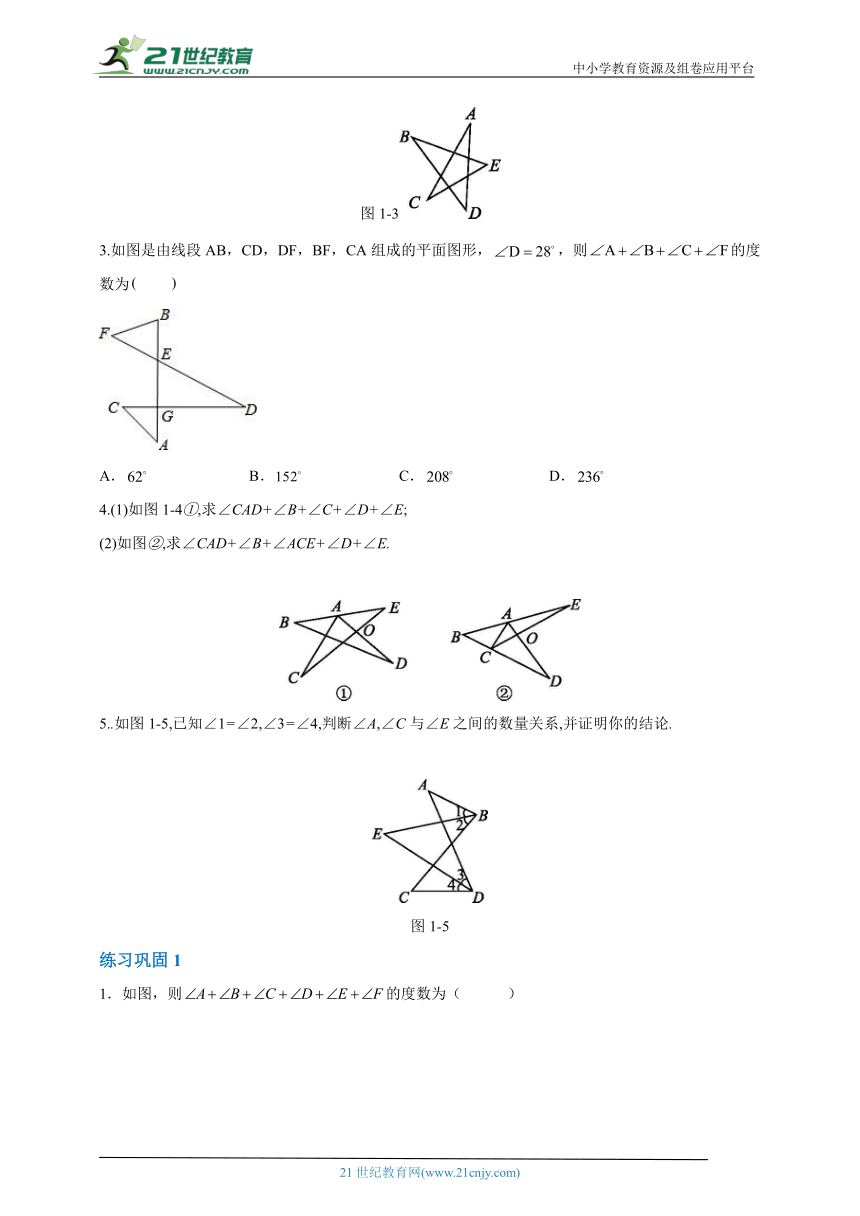
图1-3,∠A+∠B+∠C+∠D+∠E= .
图1-3
3.如图是由线段AB,CD,DF,BF,CA组成的平面图形,,则的度数为
A. B. C. D.
4.(1)如图1-4①,求∠CAD+∠B+∠C+∠D+∠E;
(2)如图②,求∠CAD+∠B+∠ACE+∠D+∠E.
5..如图1-5,已知∠1=∠2,∠3=∠4,判断∠A,∠C与∠E之间的数量关系,并证明你的结论.
图1-5
练习巩固1
1.如图,则的度数为( )
A. B. C. D.
2.图中 .
3.如图,已知:,分别平分和,其中,,求的值.
4.(1)如图1的图形我们把它称为“8字形”,则,,,四个角的数量关系是 ;
(2)如图2,若,的角平分线,交于点P,则与,的数量关系为 ;
(3)如图3,,分别平分,,当时,试求的度数(提醒:解决此问题可以直接利用上述结论);
(4)如图4,如果,,当时,试求的度数.
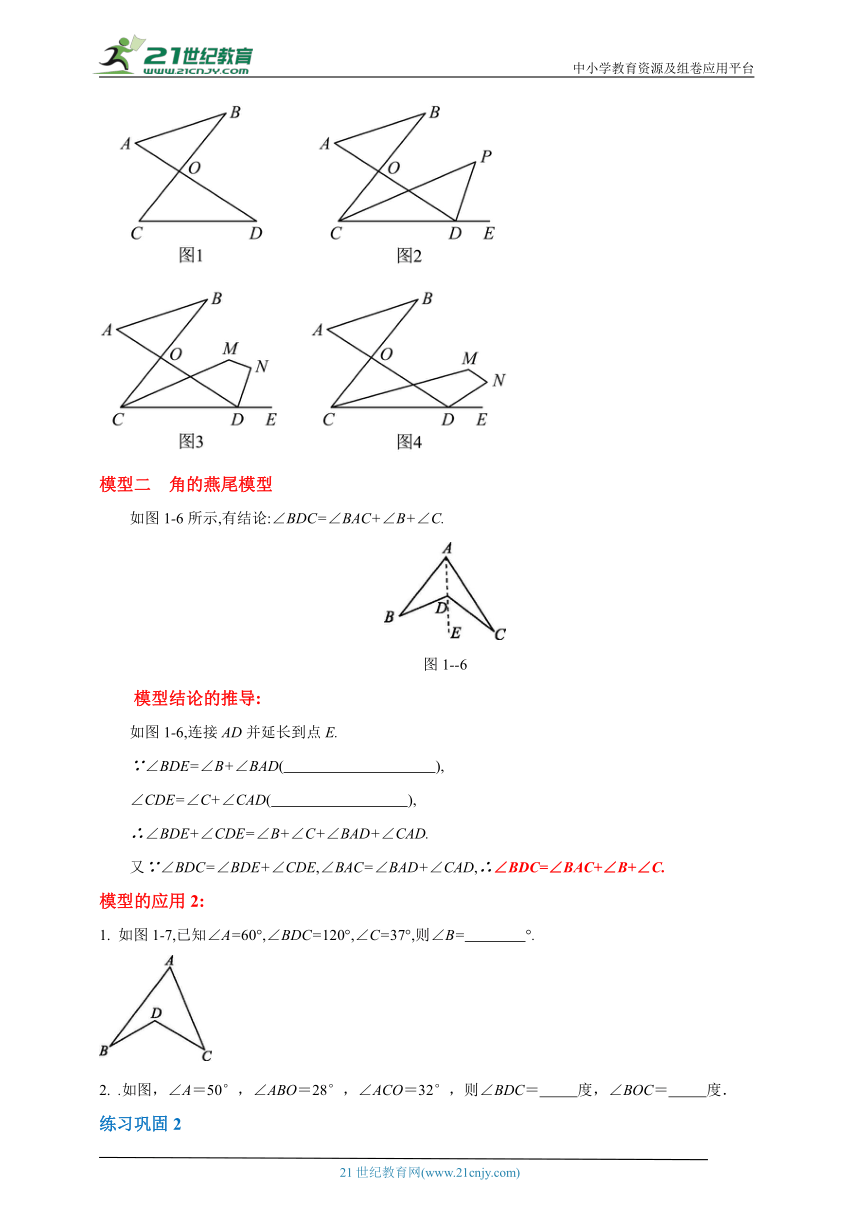
模型二 角的燕尾模型
如图1-6所示,有结论:∠BDC=∠BAC+∠B+∠C.
图1--6
模型结论的推导:
如图1-6,连接AD并延长到点E.
∵∠BDE=∠B+∠BAD( ),
∠CDE=∠C+∠CAD( ),
∴∠BDE+∠CDE=∠B+∠C+∠BAD+∠CAD.
又∵∠BDC=∠BDE+∠CDE,∠BAC=∠BAD+∠CAD,∴∠BDC=∠BAC+∠B+∠C.
模型的应用2:
如图1-7,已知∠A=60°,∠BDC=120°,∠C=37°,则∠B= °.
.如图,∠A=50°,∠ABO=28°,∠ACO=32°,则∠BDC= 度,∠BOC= 度.
练习巩固2
1.如图,∠A=50°,∠ABO=28°,∠ACO=32°,则∠BDC= 度,∠BOC= 度.
2.如图,是的平分线,CH是的平分线,与CH交于点,若,,求的度数.
3.如图1-9,求∠A+∠B+∠C+∠D+∠E+∠F.
4.如图1-10,BP,DP分别平分∠ABC与∠ADC,且交于点P,判断∠A,∠C与∠P之间的数量关系,并证明你的结论.
图1-10
模型三 角的折叠模型
折纸中的角度
如图1-11,将一张三角形纸片沿DE折叠,设∠BDA'=∠1,∠CEA'=∠2.
结论:(1)如图①,2∠A=∠1+∠2;
(2)如图②,2∠A=∠1-∠2.
模型结论的推导:
结论(1):由折叠可知,∠ADE= ,∠AED= ,而∠ADE+∠A'DE+∠1= ,∠AED+∠A'ED+∠2= ,
即∠1=180°- ,∠2=180°- ,
∴∠1+∠2=360°-2∠ADE-2∠AED=2∠A.
自己试着推导结论(2).∠1—∠2=2∠A
模型的应用3:
1.如图,三角形纸片ABC中∠A=63°,∠B=77°,将纸片一角折叠,使点C落在△ABC的内部,若∠2=50°,则∠1= .
2.探索归纳:
(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于
A.90°B.135°C.270° D.315°
(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=
(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系
是
如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.
练习巩固3
1.如图,把纸片沿DE折叠,点A落在四边形BCED的外部,,,则的度数为( )
A.32° B.30° C.28° D.26°
2.如图,在中,,将沿直线翻折,点落在点的位置,则的度数是( )
A.
B.
C.
D.
能力强化提升训练
1.如图,____________.
2.已知:如图为一五角星,求证:∠A+∠B+∠C+∠D+∠E=180°.
3.如图,∠A=51°,∠B=20°,∠C=30°,求∠BDC的度数.
4.如图,把纸片沿折叠,使点A落在图中的处,若,,则的度数为( )
A. B. C. D.
如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=__.
6.(1)已知:如图①的图形我们把它称为“字形”,试说明:.
如图②,,分别平分,,若,,求的度数.
(3)如图(3),直线平分,平分的外角,猜想与、的数量关系是________;
(4)如图(4),直线平分的外角,平分的外角,猜想与、的数量关系是________.
7.模型规律:如图1,延长交于点D,则.因为凹四边形形似箭头,其四角具有“”这个规律,所以我们把这个模型叫做“箭头四角形”.
模型应用
(1)直接应用:
①如图2,,则__________;
②如图3,__________;
(2)拓展应用:
①如图4,、的2等分线(即角平分线)、交于点,已知,,则__________;
②如图5,、分别为、的10等分线.它们的交点从上到下依次为、、、…、.已知,,则__________;
③如图6,、的角平分线、交于点D,已知,则__________;
④如图7,、的角平分线、交于点D,则、、之同的数量关系为__________.
八年级数学上分层优化堂堂清
十一章 三角形
几何模型专题
与三角形角有关的几何模型 解析版
模型一 角的“8”字模型
如图1-1所示,AC,BD相交于点O,连接AD,BC.
结论:(1)∠A+∠D=∠B+∠C.
(2)AD+BC BD+AC
图1-1
模型结论的推导:
(1)∵∠A+∠D+∠AOD=180°( ),
∠B+∠C+∠BOC=180°( ),
又∠AOD=∠BOC( ),
∴∠A+∠D=∠B+∠C.
AD①+②得:AD+BC1.如图1-2,∠A=43°,∠D=57°,∠C=37°,则∠B的度数为 .
【答案】63°
【详解】∠A+∠D=∠B+∠C.
∠B=∠A+∠D—∠C=43°+57°—37°=63°
图1-3,∠A+∠B+∠C+∠D+∠E= .
图1-3
[答案]180°
[分析] 连接CD,变为基本图形,用三角形内角和定理求解
[解析] 连接CD,∠A+∠B+∠C+∠D+∠E=∠A+∠ACD+∠ADC=180°
3.如图是由线段AB,CD,DF,BF,CA组成的平面图形,,则的度数为
A. B. C. D.
【答案】C
【解析】
【详解】
∵如图可知,,
又∵,
∴,
又∵,
∴,
又∵,
∴,
故选.
【点评】本题主要考查了三角形内角和定理即三角形外角与内角的关系,解答本题的关键是求出∠C+∠A+∠F+∠B﹣∠D=180°,此题难度不大.
4.(1)如图1-4①,求∠CAD+∠B+∠C+∠D+∠E;
(2)如图②,求∠CAD+∠B+∠ACE+∠D+∠E.
图1-4
[答案](1)180° (2)180°
.[分析] (1)连接CD,变为基本图形,用三角形内角和定理求解.
(2)连接DE,变为基本图形,用三角形内角和定理求解.
.[解析] 解:(1) 连接CD,∠CAD+∠B+∠C+∠D+∠E=∠CAD+∠ACD+∠ADC=180°
(2)连接DE,∠CAD+∠B+∠ACE+∠D+∠E.=∠B+∠BDE+∠BED=180°
5..如图1-5,已知∠1=∠2,∠3=∠4,判断∠A,∠C与∠E之间的数量关系,并证明你的结论.
图1-5
[答案]2∠E=∠A+∠C.
.[解析] 证明:由模型可知∠1+∠A=∠3+∠E,①
∠4+∠C=∠2+∠E.②
①+②,得∠1+∠A+∠4+∠C=∠3+∠E+∠2+∠E.
∵∠1=∠2,∠3=∠4,∴2∠E=∠A+∠C.
.[点评] 模型结论的推导 三角形的外角等于与它不相邻的两个内角的和 三角形的外角等于与它不相邻的两个内角的和
练习巩固1
1.如图,则的度数为( )
A. B. C. D.
【答案】B
【分析】连接,由三角形外角的性质可得:,再根据四边形内角和等于求解即可.
【详解】解:如图,连接,
由三角形外角的性质可得:,
∴
故选:B.
【点评】本题考查三角形外角的性质和四边形内角和定理,三角形外角等于不相邻的两个内角之和,四边形内角和等于.
2.图中 .
【答案】180
【分析】根据外角的性质分别得到,,等量代换,利用三角形内角和可得结果.
【详解】解:如图,∵,,
∴
故答案为:180.
【点评】本题考查的是三角形内角和定理和三角形的外角的性质,掌握三角形内角和等于和三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.
3.如图,已知:,分别平分和,其中,,求的值.
【答案】
【分析】根据三角形的外角的性质,可得,,将两式相加,结合角平分线的性质,化简即可求得答案.
【详解】∵,分别平分和,
∴,.
根据题意,得
,
.
,得
.
移项,得
.
化简,得
.
【点评】本题主要考查三角形的外角的性质和角平分线的定义,牢记三角形的外角的性质和角平分线的定义是解题的关键.
4.(1)如图1的图形我们把它称为“8字形”,则,,,四个角的数量关系是 ;
(2)如图2,若,的角平分线,交于点P,则与,的数量关系为 ;
(3)如图3,,分别平分,,当时,试求的度数(提醒:解决此问题可以直接利用上述结论);
(4)如图4,如果,,当时,试求的度数.
【答案】(1);(2);(3);(4)
【分析】(1)根据三角形内角和定理即可证明;
(2)如图2,设,,根据外角的性质得:,,所以,最后由三角形内角和定理可得结论;
(3)如图3,延长、交于点,根据(2)的结论,并将,代入可得结论;
(4)如图4,同理计算可得结论.
【详解】解:(1)在中,
,
在中,
,
∵,
∴;
故答案为:;
(2)设,,
∵,分别平分,,
∴,,
∵,
∴,
∴,
∵,
∴,
∴,
故答案为:;
(3)如图3,延长,交于点,
由(2)可知:,
∵,
∴,
∴,
∴;
(4)如图4,延长、交于点,
设,,则,
∴,,
∴,
∴,
∴,
∴,
∴,
,
,
∴
,
.
【点评】本题考查三角形内角和,三角形的外角的性质、角平分线的定义等知识,解题的关键是学会用方程的思想思考问题.
模型二 角的燕尾模型
如图1-6所示,有结论:∠BDC=∠BAC+∠B+∠C.
图1--6
模型结论的推导:
如图1-6,连接AD并延长到点E.
∵∠BDE=∠B+∠BAD( ),
∠CDE=∠C+∠CAD( ),
∴∠BDE+∠CDE=∠B+∠C+∠BAD+∠CAD.
又∵∠BDC=∠BDE+∠CDE,∠BAC=∠BAD+∠CAD,∴∠BDC=∠BAC+∠B+∠C.
如图1-7,已知∠A=60°,∠BDC=120°,∠C=37°,则∠B= °.
【答案】23°
【解析】解:∠BDC=∠A+ ∠B+ ∠C
∠B=∠BDC—∠A— ∠C=120°—60°—37°=23°
2.如图,∠A=50°,∠ABO=28°,∠ACO=32°,则∠BDC= 度,∠BOC= 度.
【答案】78°,110°
【解答】解:∵∠A=50°,∠ABO=28°,∠ACO=32°,
∴∠BDC=∠A+∠ABO=78°,
∴∠BOC=∠BDC+∠ACO=110°
练习巩固2
1.如图,∠A=50°,∠ABO=28°,∠ACO=32°,则∠BDC= 度,∠BOC= 度.
【答案】78°,110°
【解答】解:∵∠A=50°,∠ABO=28°,∠ACO=32°,
∴∠BDC=∠A+∠ABO=78°,
∴∠BOC=∠BDC+∠ACO=110°
2.如图,是的平分线,CH是的平分线,与CH交于点,若,,求的度数.
【答案】.
【解析】
【分析】
根据三角形的外角的性质得出燕尾角的基本图形的结论得出∠BDC、∠BOC,在根据角平分线的性质即可得出
【详解】
解:由燕尾角的基本图形与结论可得,
①
②
是的平分线,是的平分线
,.
①-②得,.
【点评】
本题考查了三角形的内角和定理,角平分线的定义.注意利用“8字形”的对应角相等求出角的关系是解题的关键,要注意整体思想的利用.
3.如图1-9,求∠A+∠B+∠C+∠D+∠E+∠F.
【答案】270°
【解析】解:由模型可知∠BOF=∠A+∠B+∠F,①
∠EOC=∠D+∠E+∠C,②
①+②,得∠BOF+∠EOC=∠A+∠B+∠F+∠D+∠E+∠C.
又∵∠EOC=∠BOF=135°,
∴∠A+∠B+∠C+∠D+∠E+∠F=270°.
4.如图1-10,BP,DP分别平分∠ABC与∠ADC,且交于点P,判断∠A,∠C与∠P之间的数量关系,并证明你的结论.
图1-10
【答案】∠P=(∠A-∠C).
【解析】证明:如图,由模型可知∠ADC=∠A+∠ABC+∠C.∵∠1=∠2,∠3=∠4,
∴2∠4=∠A+2∠2+∠C.①
同样由模型可知∠PDC=∠P+∠PBC+∠C,
即∠4=∠P+∠2+∠C.②
②×2-①,得∠P=(∠A-∠C).
模型三 角的折叠模型
折纸中的角度
如图1-11,将一张三角形纸片沿DE折叠,设∠BDA'=∠1,∠CEA'=∠2.
结论:(1)如图①,2∠A=∠1+∠2;
(2)如图②,2∠A=∠1-∠2.
图1-11
模型结论的推导:
结论(1):由折叠可知,∠ADE= ,∠AED= ,而∠ADE+∠A'DE+∠1= ,∠AED+∠A'ED+∠2= ,
即∠1=180°- ,∠2=180°- ,
∴∠1+∠2=360°-2∠ADE-2∠AED=2∠A.
自己试着推导结论(2).∠1—∠2=2∠A
模型的应用:
1.如图,三角形纸片ABC中∠A=63°,∠B=77°,将纸片一角折叠,使点C落在△ABC的内部,若∠2=50°,则∠1= .
【答案】30°
【解答】解:设折痕为EF,连接CC′.
∵∠2=∠ECC′+∠EC′C,∠1=∠FCC′+∠FC′C,∠ECF=∠EC′F,
∴∠1+∠2=2∠ECF,
∵∠C=180°﹣∠A﹣∠B=180°﹣63°﹣77°=40°,
∴∠1=80°﹣50°=30°,
故答案为:30°
2.探索归纳:
(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于
A.90°B.135°C.270° D.315°
(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=
(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系
是
(4)如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.
【解答】解:(1):∵四边形的内角和为360°,直角三角形中两个锐角和为90°
∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.
∴∠1+∠2等于270°.
故选C;
(2)∠1+∠2=180°+40°=220°,
故答案是:220°;
(3)∠1+∠2与∠A的关系是:∠1+∠2=180°+∠A
(4)∵△EFP是由△EFA折叠得到的,
∴∠AFE=∠PFE,∠AEF=∠PEF
∴∠1=180°﹣2∠AFE,∠2=180°﹣2∠AEF
∴∠1+∠2=360°﹣2(∠AFE+∠AEF)
又∵∠AFE+∠AEF=180°﹣∠A,
∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A.
练习巩固3
1.如图,把纸片沿DE折叠,点A落在四边形BCED的外部,,,则的度数为( )
A.32° B.30° C.28° D.26°
【答案】C
【分析】根据翻折的性质可得,再利用三角形外角的性质表示出,然后根据角的和差整理即可得解.
【详解】解:如图,由翻折的性质得,
∴,
∴在△ADE中,,
∵,
∴,
∴,
∵,,
∴.
故选:C.
【点评】本题考查了翻折变换的性质,三角形外角的性质,理解折叠前后对应角相等是解题关键.
2.如图,在中,,将沿直线翻折,点落在点的位置,则的度数是( )
A.
B.
C.
D.
【答案】D
【解析】
【分析】
本题考查三角形外角性质,解题的关键是熟练掌握基本知识,属于中考常考题型.
由题意得到,再利用外角性质得出,即可求解.
【解答】
解:如图所示:
由题意得:,
根据外角性质得:,,
,
.
故选:.
能力强化提升训练
1.如图,____________.
【答案】
【分析】根据三角形外角的性质可得∠BAC=∠C+∠E,∠DAE=∠B+∠D,根据平角的定义即可得答案.
【详解】∵∠BAC和∠DAE分别是△ACE和△ABD的外角,
∴∠BAC=∠C+∠E,∠DAE=∠B+∠D,
∴∠CAD+∠BAC+∠DAE=180°,
故答案为:180°
【点评】本题考查三角形外角性质,三角形的一个外角等于与它不相邻的两个内角的和;熟练掌握外角性质是解题关键.
2.已知:如图为一五角星,求证:∠A+∠B+∠C+∠D+∠E=180°.
解析:根据三角形外角性质得出∠EFG=∠B+∠D,∠EGF=∠A+∠C,根据三角形内角和定理得出∠E+∠EGF+∠EFG=180°,代入即可得证.
证明:∵∠EFG、∠EGF分别是△BDF、△ACG的外角,∴∠EFG=∠B+∠D,∠EGF=∠A+∠C.又∵在△EFG中,∠E+∠EGF+∠EFG=180°,∴∠A+∠B+∠C+∠D+∠E=180°.
方法总结:解决此类问题的关键是根据图形的特点,利用三角形外角的性质将分散的角集中到某个三角形中,利用三角形内角和进行解决.
3.如图,∠A=51°,∠B=20°,∠C=30°,求∠BDC的度数.
思路点拨:添加适当的辅助线将四边形问题转化为三角形问题.
解法一:连接AD并延长于点E.
在△ABD中,∠1+∠ABD=∠3,
在△ACD中,∠2+∠ACD=∠4.
因为∠BDC=∠3+∠4,∠BAC=∠1+∠2,
所以∠BDC=∠BAC+∠ABD+∠ACD
=51° +20°+30°=101°.
解法二:延长BD交AC于点E.
在△ABE中,∠1=∠ABE+∠BAE,
在△ECD中,∠BDC=∠1+∠ECD.
所以∠BDC=∠BAC+∠ABD+∠ACD=51°+20°+30°=101°.
解法三:连接延长CD交AB于点F(解题过程同解法二).
4.如图,把纸片沿折叠,使点A落在图中的处,若,,则的度数为( )
A. B. C. D.
【答案】A
【分析】利用折叠性质得,,再根据三角形外角性质得,利用邻补角得到,则,然后利用,进行计算即可.
【详解】解:,
,
纸片沿折叠,使点A落在图中的处,
°,,
,
,
,
,
故选:A.
【点评】本题考查了折叠的性质,三角形外角的性质,求一个角的邻补角,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=__.
【答案】900°
【解析】
【分析】
根据多边形的内角和,可得答案.
【详解】
解:连EF,GI,如图
,
∵6边形ABCDEFK的内角和=(6-2)×180°=720°,
∴∠A+∠B+∠C+∠D+∠E+∠F=720°-(∠1+∠2),
即∠A+∠B+∠C+∠D+∠E+∠F+(∠1+∠2)=720°,
∵∠1+∠2=∠3+∠4,∠5+∠6+∠H=180°,
∴∠A+∠B+∠C+∠D+∠E+∠F∠H+(∠3+∠4)=900°,
∴∠A+∠B+∠C+∠D+∠E+∠F(∠3+∠4)+∠5+∠6+∠H=720°+180°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=900°,
故答案为:900°.
【点睛】
本题考查了n边形的内角和定理:n边形的内角和为(n-2)×180°(n≥3的整数).
6.(1)已知:如图①的图形我们把它称为“字形”,试说明:.
如图②,,分别平分,,若,,求的度数.
(3)如图(3),直线平分,平分的外角,猜想与、的数量关系是________;
(4)如图(4),直线平分的外角,平分的外角,猜想与、的数量关系是________.
【答案】(1)见解析;(2)26°;(3);(4)
【解析】
【分析】
(1)根据三角形的内角和等于180°和对顶角的性质即可得证;
(2)设,,解方程即可得到答案;
(3)根据直线平分,平分的外角,得到
,从而可以得到180°,再根据∠P+∠PAD=∠PCD+∠D,∠BAD+∠B=∠BCD+∠D得到即可求解;
(4)连接PB,PD根据180°,180°得到360°,同理得到:360°,再根据180°,180°,,,即可求解.
【详解】
解:(1)180°,180°,
.
,
;
(2),分别平分,,设,,
则有,
,
(36°+16°)=26°
(3)直线平分,平分的外角,
,,
∴180°-,
∴180°
∵∠P+∠PAD=∠PCD+∠D,∠BAD+∠B=∠BCD+∠D
∴
∴
∴180°,
即90°.
(4)连接PB,PD
直线平分的外角,平分的外角,
,,
∵180°,180°
∴360°
同理得到:360°
∴720°
∴720°
∵180°,180°
∴360°,
180°-
【点评】
本题主要考查了角平分线的定义,三角形内角和定理,解题的关键在于能够熟练掌握相关知识进行求解.
7.模型规律:如图1,延长交于点D,则.因为凹四边形形似箭头,其四角具有“”这个规律,所以我们把这个模型叫做“箭头四角形”.
模型应用
(1)直接应用:
①如图2,,则__________;
②如图3,__________;
(2)拓展应用:
①如图4,、的2等分线(即角平分线)、交于点,已知,,则__________;
②如图5,、分别为、的10等分线.它们的交点从上到下依次为、、、…、.已知,,则__________;
③如图6,、的角平分线、交于点D,已知,则__________;
④如图7,、的角平分线、交于点D,则、、之同的数量关系为__________.
【答案】(1)①110;②260;(2)①85;②99;③142;④∠B-∠C+2∠D=0
【解析】
【分析】
(1)①根据题干中的等式直接计算即可;
②同理可得∠A+∠B+∠C+∠D+∠E+∠F=∠BOC+∠DOE,代入计算即可;
(2)①同理可得∠BO1C=∠BOC-∠OBO1-∠OCO1,代入计算可得;
②同理可得∠BO7C=∠BOC-(∠BOC-∠A),代入计算即可;
③利用∠ADB=180°-(∠ABD+∠BAD)=180°-(∠BOC-∠C)计算可得;
④根据两个凹四边形ABOD和ABOC得到两个等式,联立可得结论.
【详解】
解:(1)①∠BOC=∠A+∠B+∠C=60°+20°+30°=110°;
②∠A+∠B+∠C+∠D+∠E+∠F=∠BOC+∠DOE=2×130°=260°;
(2)①∠BO1C=∠BOC-∠OBO1-∠OCO1
=∠BOC-(∠ABO+∠ACO)
=∠BOC-(∠BOC-∠A)
=∠BOC-(120°-50°)
=120°-35°
=85°;
②∠BO7C=∠BOC-(∠BOC-∠A)
=120°-(120°-50°)
=120°-21°
=99°;
③∠ADB=180°-(∠ABD+∠BAD)
=180°-(∠BOC-∠C)
=180°-(120°-44°)
=142°;
④∠BOD=∠BOC=∠B+∠D+∠BAC,
∠BOC=∠B+∠C+∠BAC,
联立得:∠B-∠C+2∠D=0.
【点评】
本题主要考查了新定义—箭头四角形,利用了三角形外角的性质,还考查了角平分线的定义,图形类规律,解题的关键是理解箭头四角形,并能熟练运用其性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
八年级数学上分层优化堂堂清
十一章 三角形
几何模型专题
与三角形角有关的几何模型(一)
模型一 角的“8”字模型
如图1-1所示,AC,BD相交于点O,连接AD,BC.
结论:(1)∠A+∠D=∠B+∠C.
(2)AD+BC BD+AC
图1-1
模型结论的推导:
(1)∵∠A+∠D+∠AOD=180°( ),
∠B+∠C+∠BOC=180°( ),
又∠AOD=∠BOC( ),
∴∠A+∠D=∠B+∠C.
AD
1.如图1-2,∠A=43°,∠D=57°,∠C=37°,则∠B的度数为 .
图1-3,∠A+∠B+∠C+∠D+∠E= .
图1-3
3.如图是由线段AB,CD,DF,BF,CA组成的平面图形,,则的度数为
A. B. C. D.
4.(1)如图1-4①,求∠CAD+∠B+∠C+∠D+∠E;
(2)如图②,求∠CAD+∠B+∠ACE+∠D+∠E.
5..如图1-5,已知∠1=∠2,∠3=∠4,判断∠A,∠C与∠E之间的数量关系,并证明你的结论.
图1-5
练习巩固1
1.如图,则的度数为( )
A. B. C. D.
2.图中 .
3.如图,已知:,分别平分和,其中,,求的值.
4.(1)如图1的图形我们把它称为“8字形”,则,,,四个角的数量关系是 ;
(2)如图2,若,的角平分线,交于点P,则与,的数量关系为 ;
(3)如图3,,分别平分,,当时,试求的度数(提醒:解决此问题可以直接利用上述结论);
(4)如图4,如果,,当时,试求的度数.
模型二 角的燕尾模型
如图1-6所示,有结论:∠BDC=∠BAC+∠B+∠C.
图1--6
模型结论的推导:
如图1-6,连接AD并延长到点E.
∵∠BDE=∠B+∠BAD( ),
∠CDE=∠C+∠CAD( ),
∴∠BDE+∠CDE=∠B+∠C+∠BAD+∠CAD.
又∵∠BDC=∠BDE+∠CDE,∠BAC=∠BAD+∠CAD,∴∠BDC=∠BAC+∠B+∠C.
模型的应用2:
如图1-7,已知∠A=60°,∠BDC=120°,∠C=37°,则∠B= °.
.如图,∠A=50°,∠ABO=28°,∠ACO=32°,则∠BDC= 度,∠BOC= 度.
练习巩固2
1.如图,∠A=50°,∠ABO=28°,∠ACO=32°,则∠BDC= 度,∠BOC= 度.
2.如图,是的平分线,CH是的平分线,与CH交于点,若,,求的度数.
3.如图1-9,求∠A+∠B+∠C+∠D+∠E+∠F.
4.如图1-10,BP,DP分别平分∠ABC与∠ADC,且交于点P,判断∠A,∠C与∠P之间的数量关系,并证明你的结论.
图1-10
模型三 角的折叠模型
折纸中的角度
如图1-11,将一张三角形纸片沿DE折叠,设∠BDA'=∠1,∠CEA'=∠2.
结论:(1)如图①,2∠A=∠1+∠2;
(2)如图②,2∠A=∠1-∠2.
模型结论的推导:
结论(1):由折叠可知,∠ADE= ,∠AED= ,而∠ADE+∠A'DE+∠1= ,∠AED+∠A'ED+∠2= ,
即∠1=180°- ,∠2=180°- ,
∴∠1+∠2=360°-2∠ADE-2∠AED=2∠A.
自己试着推导结论(2).∠1—∠2=2∠A
模型的应用3:
1.如图,三角形纸片ABC中∠A=63°,∠B=77°,将纸片一角折叠,使点C落在△ABC的内部,若∠2=50°,则∠1= .
2.探索归纳:
(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于
A.90°B.135°C.270° D.315°
(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=
(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系
是
如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.
练习巩固3
1.如图,把纸片沿DE折叠,点A落在四边形BCED的外部,,,则的度数为( )
A.32° B.30° C.28° D.26°
2.如图,在中,,将沿直线翻折,点落在点的位置,则的度数是( )
A.
B.
C.
D.
能力强化提升训练
1.如图,____________.
2.已知:如图为一五角星,求证:∠A+∠B+∠C+∠D+∠E=180°.
3.如图,∠A=51°,∠B=20°,∠C=30°,求∠BDC的度数.
4.如图,把纸片沿折叠,使点A落在图中的处,若,,则的度数为( )
A. B. C. D.
如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=__.
6.(1)已知:如图①的图形我们把它称为“字形”,试说明:.
如图②,,分别平分,,若,,求的度数.
(3)如图(3),直线平分,平分的外角,猜想与、的数量关系是________;
(4)如图(4),直线平分的外角,平分的外角,猜想与、的数量关系是________.
7.模型规律:如图1,延长交于点D,则.因为凹四边形形似箭头,其四角具有“”这个规律,所以我们把这个模型叫做“箭头四角形”.
模型应用
(1)直接应用:
①如图2,,则__________;
②如图3,__________;
(2)拓展应用:
①如图4,、的2等分线(即角平分线)、交于点,已知,,则__________;
②如图5,、分别为、的10等分线.它们的交点从上到下依次为、、、…、.已知,,则__________;
③如图6,、的角平分线、交于点D,已知,则__________;
④如图7,、的角平分线、交于点D,则、、之同的数量关系为__________.
八年级数学上分层优化堂堂清
十一章 三角形
几何模型专题
与三角形角有关的几何模型 解析版
模型一 角的“8”字模型
如图1-1所示,AC,BD相交于点O,连接AD,BC.
结论:(1)∠A+∠D=∠B+∠C.
(2)AD+BC BD+AC
图1-1
模型结论的推导:
(1)∵∠A+∠D+∠AOD=180°( ),
∠B+∠C+∠BOC=180°( ),
又∠AOD=∠BOC( ),
∴∠A+∠D=∠B+∠C.
AD
【答案】63°
【详解】∠A+∠D=∠B+∠C.
∠B=∠A+∠D—∠C=43°+57°—37°=63°
图1-3,∠A+∠B+∠C+∠D+∠E= .
图1-3
[答案]180°
[分析] 连接CD,变为基本图形,用三角形内角和定理求解
[解析] 连接CD,∠A+∠B+∠C+∠D+∠E=∠A+∠ACD+∠ADC=180°
3.如图是由线段AB,CD,DF,BF,CA组成的平面图形,,则的度数为
A. B. C. D.
【答案】C
【解析】
【详解】
∵如图可知,,
又∵,
∴,
又∵,
∴,
又∵,
∴,
故选.
【点评】本题主要考查了三角形内角和定理即三角形外角与内角的关系,解答本题的关键是求出∠C+∠A+∠F+∠B﹣∠D=180°,此题难度不大.
4.(1)如图1-4①,求∠CAD+∠B+∠C+∠D+∠E;
(2)如图②,求∠CAD+∠B+∠ACE+∠D+∠E.
图1-4
[答案](1)180° (2)180°
.[分析] (1)连接CD,变为基本图形,用三角形内角和定理求解.
(2)连接DE,变为基本图形,用三角形内角和定理求解.
.[解析] 解:(1) 连接CD,∠CAD+∠B+∠C+∠D+∠E=∠CAD+∠ACD+∠ADC=180°
(2)连接DE,∠CAD+∠B+∠ACE+∠D+∠E.=∠B+∠BDE+∠BED=180°
5..如图1-5,已知∠1=∠2,∠3=∠4,判断∠A,∠C与∠E之间的数量关系,并证明你的结论.
图1-5
[答案]2∠E=∠A+∠C.
.[解析] 证明:由模型可知∠1+∠A=∠3+∠E,①
∠4+∠C=∠2+∠E.②
①+②,得∠1+∠A+∠4+∠C=∠3+∠E+∠2+∠E.
∵∠1=∠2,∠3=∠4,∴2∠E=∠A+∠C.
.[点评] 模型结论的推导 三角形的外角等于与它不相邻的两个内角的和 三角形的外角等于与它不相邻的两个内角的和
练习巩固1
1.如图,则的度数为( )
A. B. C. D.
【答案】B
【分析】连接,由三角形外角的性质可得:,再根据四边形内角和等于求解即可.
【详解】解:如图,连接,
由三角形外角的性质可得:,
∴
故选:B.
【点评】本题考查三角形外角的性质和四边形内角和定理,三角形外角等于不相邻的两个内角之和,四边形内角和等于.
2.图中 .
【答案】180
【分析】根据外角的性质分别得到,,等量代换,利用三角形内角和可得结果.
【详解】解:如图,∵,,
∴
故答案为:180.
【点评】本题考查的是三角形内角和定理和三角形的外角的性质,掌握三角形内角和等于和三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.
3.如图,已知:,分别平分和,其中,,求的值.
【答案】
【分析】根据三角形的外角的性质,可得,,将两式相加,结合角平分线的性质,化简即可求得答案.
【详解】∵,分别平分和,
∴,.
根据题意,得
,
.
,得
.
移项,得
.
化简,得
.
【点评】本题主要考查三角形的外角的性质和角平分线的定义,牢记三角形的外角的性质和角平分线的定义是解题的关键.
4.(1)如图1的图形我们把它称为“8字形”,则,,,四个角的数量关系是 ;
(2)如图2,若,的角平分线,交于点P,则与,的数量关系为 ;
(3)如图3,,分别平分,,当时,试求的度数(提醒:解决此问题可以直接利用上述结论);
(4)如图4,如果,,当时,试求的度数.
【答案】(1);(2);(3);(4)
【分析】(1)根据三角形内角和定理即可证明;
(2)如图2,设,,根据外角的性质得:,,所以,最后由三角形内角和定理可得结论;
(3)如图3,延长、交于点,根据(2)的结论,并将,代入可得结论;
(4)如图4,同理计算可得结论.
【详解】解:(1)在中,
,
在中,
,
∵,
∴;
故答案为:;
(2)设,,
∵,分别平分,,
∴,,
∵,
∴,
∴,
∵,
∴,
∴,
故答案为:;
(3)如图3,延长,交于点,
由(2)可知:,
∵,
∴,
∴,
∴;
(4)如图4,延长、交于点,
设,,则,
∴,,
∴,
∴,
∴,
∴,
∴,
,
,
∴
,
.
【点评】本题考查三角形内角和,三角形的外角的性质、角平分线的定义等知识,解题的关键是学会用方程的思想思考问题.
模型二 角的燕尾模型
如图1-6所示,有结论:∠BDC=∠BAC+∠B+∠C.
图1--6
模型结论的推导:
如图1-6,连接AD并延长到点E.
∵∠BDE=∠B+∠BAD( ),
∠CDE=∠C+∠CAD( ),
∴∠BDE+∠CDE=∠B+∠C+∠BAD+∠CAD.
又∵∠BDC=∠BDE+∠CDE,∠BAC=∠BAD+∠CAD,∴∠BDC=∠BAC+∠B+∠C.
如图1-7,已知∠A=60°,∠BDC=120°,∠C=37°,则∠B= °.
【答案】23°
【解析】解:∠BDC=∠A+ ∠B+ ∠C
∠B=∠BDC—∠A— ∠C=120°—60°—37°=23°
2.如图,∠A=50°,∠ABO=28°,∠ACO=32°,则∠BDC= 度,∠BOC= 度.
【答案】78°,110°
【解答】解:∵∠A=50°,∠ABO=28°,∠ACO=32°,
∴∠BDC=∠A+∠ABO=78°,
∴∠BOC=∠BDC+∠ACO=110°
练习巩固2
1.如图,∠A=50°,∠ABO=28°,∠ACO=32°,则∠BDC= 度,∠BOC= 度.
【答案】78°,110°
【解答】解:∵∠A=50°,∠ABO=28°,∠ACO=32°,
∴∠BDC=∠A+∠ABO=78°,
∴∠BOC=∠BDC+∠ACO=110°
2.如图,是的平分线,CH是的平分线,与CH交于点,若,,求的度数.
【答案】.
【解析】
【分析】
根据三角形的外角的性质得出燕尾角的基本图形的结论得出∠BDC、∠BOC,在根据角平分线的性质即可得出
【详解】
解:由燕尾角的基本图形与结论可得,
①
②
是的平分线,是的平分线
,.
①-②得,.
【点评】
本题考查了三角形的内角和定理,角平分线的定义.注意利用“8字形”的对应角相等求出角的关系是解题的关键,要注意整体思想的利用.
3.如图1-9,求∠A+∠B+∠C+∠D+∠E+∠F.
【答案】270°
【解析】解:由模型可知∠BOF=∠A+∠B+∠F,①
∠EOC=∠D+∠E+∠C,②
①+②,得∠BOF+∠EOC=∠A+∠B+∠F+∠D+∠E+∠C.
又∵∠EOC=∠BOF=135°,
∴∠A+∠B+∠C+∠D+∠E+∠F=270°.
4.如图1-10,BP,DP分别平分∠ABC与∠ADC,且交于点P,判断∠A,∠C与∠P之间的数量关系,并证明你的结论.
图1-10
【答案】∠P=(∠A-∠C).
【解析】证明:如图,由模型可知∠ADC=∠A+∠ABC+∠C.∵∠1=∠2,∠3=∠4,
∴2∠4=∠A+2∠2+∠C.①
同样由模型可知∠PDC=∠P+∠PBC+∠C,
即∠4=∠P+∠2+∠C.②
②×2-①,得∠P=(∠A-∠C).
模型三 角的折叠模型
折纸中的角度
如图1-11,将一张三角形纸片沿DE折叠,设∠BDA'=∠1,∠CEA'=∠2.
结论:(1)如图①,2∠A=∠1+∠2;
(2)如图②,2∠A=∠1-∠2.
图1-11
模型结论的推导:
结论(1):由折叠可知,∠ADE= ,∠AED= ,而∠ADE+∠A'DE+∠1= ,∠AED+∠A'ED+∠2= ,
即∠1=180°- ,∠2=180°- ,
∴∠1+∠2=360°-2∠ADE-2∠AED=2∠A.
自己试着推导结论(2).∠1—∠2=2∠A
模型的应用:
1.如图,三角形纸片ABC中∠A=63°,∠B=77°,将纸片一角折叠,使点C落在△ABC的内部,若∠2=50°,则∠1= .
【答案】30°
【解答】解:设折痕为EF,连接CC′.
∵∠2=∠ECC′+∠EC′C,∠1=∠FCC′+∠FC′C,∠ECF=∠EC′F,
∴∠1+∠2=2∠ECF,
∵∠C=180°﹣∠A﹣∠B=180°﹣63°﹣77°=40°,
∴∠1=80°﹣50°=30°,
故答案为:30°
2.探索归纳:
(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于
A.90°B.135°C.270° D.315°
(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=
(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系
是
(4)如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.
【解答】解:(1):∵四边形的内角和为360°,直角三角形中两个锐角和为90°
∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.
∴∠1+∠2等于270°.
故选C;
(2)∠1+∠2=180°+40°=220°,
故答案是:220°;
(3)∠1+∠2与∠A的关系是:∠1+∠2=180°+∠A
(4)∵△EFP是由△EFA折叠得到的,
∴∠AFE=∠PFE,∠AEF=∠PEF
∴∠1=180°﹣2∠AFE,∠2=180°﹣2∠AEF
∴∠1+∠2=360°﹣2(∠AFE+∠AEF)
又∵∠AFE+∠AEF=180°﹣∠A,
∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A.
练习巩固3
1.如图,把纸片沿DE折叠,点A落在四边形BCED的外部,,,则的度数为( )
A.32° B.30° C.28° D.26°
【答案】C
【分析】根据翻折的性质可得,再利用三角形外角的性质表示出,然后根据角的和差整理即可得解.
【详解】解:如图,由翻折的性质得,
∴,
∴在△ADE中,,
∵,
∴,
∴,
∵,,
∴.
故选:C.
【点评】本题考查了翻折变换的性质,三角形外角的性质,理解折叠前后对应角相等是解题关键.
2.如图,在中,,将沿直线翻折,点落在点的位置,则的度数是( )
A.
B.
C.
D.
【答案】D
【解析】
【分析】
本题考查三角形外角性质,解题的关键是熟练掌握基本知识,属于中考常考题型.
由题意得到,再利用外角性质得出,即可求解.
【解答】
解:如图所示:
由题意得:,
根据外角性质得:,,
,
.
故选:.
能力强化提升训练
1.如图,____________.
【答案】
【分析】根据三角形外角的性质可得∠BAC=∠C+∠E,∠DAE=∠B+∠D,根据平角的定义即可得答案.
【详解】∵∠BAC和∠DAE分别是△ACE和△ABD的外角,
∴∠BAC=∠C+∠E,∠DAE=∠B+∠D,
∴∠CAD+∠BAC+∠DAE=180°,
故答案为:180°
【点评】本题考查三角形外角性质,三角形的一个外角等于与它不相邻的两个内角的和;熟练掌握外角性质是解题关键.
2.已知:如图为一五角星,求证:∠A+∠B+∠C+∠D+∠E=180°.
解析:根据三角形外角性质得出∠EFG=∠B+∠D,∠EGF=∠A+∠C,根据三角形内角和定理得出∠E+∠EGF+∠EFG=180°,代入即可得证.
证明:∵∠EFG、∠EGF分别是△BDF、△ACG的外角,∴∠EFG=∠B+∠D,∠EGF=∠A+∠C.又∵在△EFG中,∠E+∠EGF+∠EFG=180°,∴∠A+∠B+∠C+∠D+∠E=180°.
方法总结:解决此类问题的关键是根据图形的特点,利用三角形外角的性质将分散的角集中到某个三角形中,利用三角形内角和进行解决.
3.如图,∠A=51°,∠B=20°,∠C=30°,求∠BDC的度数.
思路点拨:添加适当的辅助线将四边形问题转化为三角形问题.
解法一:连接AD并延长于点E.
在△ABD中,∠1+∠ABD=∠3,
在△ACD中,∠2+∠ACD=∠4.
因为∠BDC=∠3+∠4,∠BAC=∠1+∠2,
所以∠BDC=∠BAC+∠ABD+∠ACD
=51° +20°+30°=101°.
解法二:延长BD交AC于点E.
在△ABE中,∠1=∠ABE+∠BAE,
在△ECD中,∠BDC=∠1+∠ECD.
所以∠BDC=∠BAC+∠ABD+∠ACD=51°+20°+30°=101°.
解法三:连接延长CD交AB于点F(解题过程同解法二).
4.如图,把纸片沿折叠,使点A落在图中的处,若,,则的度数为( )
A. B. C. D.
【答案】A
【分析】利用折叠性质得,,再根据三角形外角性质得,利用邻补角得到,则,然后利用,进行计算即可.
【详解】解:,
,
纸片沿折叠,使点A落在图中的处,
°,,
,
,
,
,
故选:A.
【点评】本题考查了折叠的性质,三角形外角的性质,求一个角的邻补角,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=__.
【答案】900°
【解析】
【分析】
根据多边形的内角和,可得答案.
【详解】
解:连EF,GI,如图
,
∵6边形ABCDEFK的内角和=(6-2)×180°=720°,
∴∠A+∠B+∠C+∠D+∠E+∠F=720°-(∠1+∠2),
即∠A+∠B+∠C+∠D+∠E+∠F+(∠1+∠2)=720°,
∵∠1+∠2=∠3+∠4,∠5+∠6+∠H=180°,
∴∠A+∠B+∠C+∠D+∠E+∠F∠H+(∠3+∠4)=900°,
∴∠A+∠B+∠C+∠D+∠E+∠F(∠3+∠4)+∠5+∠6+∠H=720°+180°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=900°,
故答案为:900°.
【点睛】
本题考查了n边形的内角和定理:n边形的内角和为(n-2)×180°(n≥3的整数).
6.(1)已知:如图①的图形我们把它称为“字形”,试说明:.
如图②,,分别平分,,若,,求的度数.
(3)如图(3),直线平分,平分的外角,猜想与、的数量关系是________;
(4)如图(4),直线平分的外角,平分的外角,猜想与、的数量关系是________.
【答案】(1)见解析;(2)26°;(3);(4)
【解析】
【分析】
(1)根据三角形的内角和等于180°和对顶角的性质即可得证;
(2)设,,解方程即可得到答案;
(3)根据直线平分,平分的外角,得到
,从而可以得到180°,再根据∠P+∠PAD=∠PCD+∠D,∠BAD+∠B=∠BCD+∠D得到即可求解;
(4)连接PB,PD根据180°,180°得到360°,同理得到:360°,再根据180°,180°,,,即可求解.
【详解】
解:(1)180°,180°,
.
,
;
(2),分别平分,,设,,
则有,
,
(36°+16°)=26°
(3)直线平分,平分的外角,
,,
∴180°-,
∴180°
∵∠P+∠PAD=∠PCD+∠D,∠BAD+∠B=∠BCD+∠D
∴
∴
∴180°,
即90°.
(4)连接PB,PD
直线平分的外角,平分的外角,
,,
∵180°,180°
∴360°
同理得到:360°
∴720°
∴720°
∵180°,180°
∴360°,
180°-
【点评】
本题主要考查了角平分线的定义,三角形内角和定理,解题的关键在于能够熟练掌握相关知识进行求解.
7.模型规律:如图1,延长交于点D,则.因为凹四边形形似箭头,其四角具有“”这个规律,所以我们把这个模型叫做“箭头四角形”.
模型应用
(1)直接应用:
①如图2,,则__________;
②如图3,__________;
(2)拓展应用:
①如图4,、的2等分线(即角平分线)、交于点,已知,,则__________;
②如图5,、分别为、的10等分线.它们的交点从上到下依次为、、、…、.已知,,则__________;
③如图6,、的角平分线、交于点D,已知,则__________;
④如图7,、的角平分线、交于点D,则、、之同的数量关系为__________.
【答案】(1)①110;②260;(2)①85;②99;③142;④∠B-∠C+2∠D=0
【解析】
【分析】
(1)①根据题干中的等式直接计算即可;
②同理可得∠A+∠B+∠C+∠D+∠E+∠F=∠BOC+∠DOE,代入计算即可;
(2)①同理可得∠BO1C=∠BOC-∠OBO1-∠OCO1,代入计算可得;
②同理可得∠BO7C=∠BOC-(∠BOC-∠A),代入计算即可;
③利用∠ADB=180°-(∠ABD+∠BAD)=180°-(∠BOC-∠C)计算可得;
④根据两个凹四边形ABOD和ABOC得到两个等式,联立可得结论.
【详解】
解:(1)①∠BOC=∠A+∠B+∠C=60°+20°+30°=110°;
②∠A+∠B+∠C+∠D+∠E+∠F=∠BOC+∠DOE=2×130°=260°;
(2)①∠BO1C=∠BOC-∠OBO1-∠OCO1
=∠BOC-(∠ABO+∠ACO)
=∠BOC-(∠BOC-∠A)
=∠BOC-(120°-50°)
=120°-35°
=85°;
②∠BO7C=∠BOC-(∠BOC-∠A)
=120°-(120°-50°)
=120°-21°
=99°;
③∠ADB=180°-(∠ABD+∠BAD)
=180°-(∠BOC-∠C)
=180°-(120°-44°)
=142°;
④∠BOD=∠BOC=∠B+∠D+∠BAC,
∠BOC=∠B+∠C+∠BAC,
联立得:∠B-∠C+2∠D=0.
【点评】
本题主要考查了新定义—箭头四角形,利用了三角形外角的性质,还考查了角平分线的定义,图形类规律,解题的关键是理解箭头四角形,并能熟练运用其性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
