八年级数学上分层优化堂堂清(10)11.3.2 多边形的内角和(含解析)
文档属性
| 名称 | 八年级数学上分层优化堂堂清(10)11.3.2 多边形的内角和(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 21:08:50 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
八年级数学上分层优化堂堂清
十一章 三角形
11.3多边形及其内角和
11.3.2 多边形的内角和
学习目标:
1.能通过不同方法探索多边形的内角和与外角和公式.
2.学会运用多边形的内角和与外角和公式解决问题.
老师对你说:
多边形的内角和
多边形的内角和公式:n边形的内角和等于(n-2)×180°。
多边形的内角和推理方法
方法1:如图1所示,从n边形的一个顶点引出(n-3)条对角线,这(n-3)条对角线把n边形分成(n-2)个三角形,每个三角形的内角和是180°,所以n边形的内角和为(n-2)×180°。
方法2:如图2所示,在n边形内任取一点P,连接PA1,PA2……PAn,把n边形分成n个三角形,这n个三角形的内角和为n ×180°,再减去一个周角,即得n边形的内角和为n×180° -360°=(n-2)×180°。
方法3:如图3所示,如图所示,在n边形的 一边上任取一点P与各顶点相连,得(n-1)个三角形,n边形内角和等于这(n-1)个三角形的内角和减去在点P 处的一个平角,即得n边形的内角和为(n-1)×180° -180° =(n-2)×180°。
多边形的外角和
性质:多边形的外角和等于360°。
基础提升 教材核心知识点精练
知识点1:多边形的内角和
【例1-1】一个多边形的内角和为1800°,则这个多边形为( )
A.九边形 B.十边形 C.十一边形 D.十二边形
【例1-2】一个多边形的内角和的度数可能是( )
A.2700° B.2800° C.2900° D.3000°
【例1-3】如图,一束太阳光线平行照射在放置于地面的正六边形上,若,则的度数为( )
A. B. C. D.
知识点2:多边形的外角和
【例2-1】如图,小明从正八边形(各边相等,各内角也相等)草地的一边AB上一点S出发,步行一周回到原处在步行的过程中,小明转过的角度的和是( )
A. B. C. D.
【例2-2】若一个多边形的内角和与外角和之比是的5︰2,则这个多边形的边数是__________.
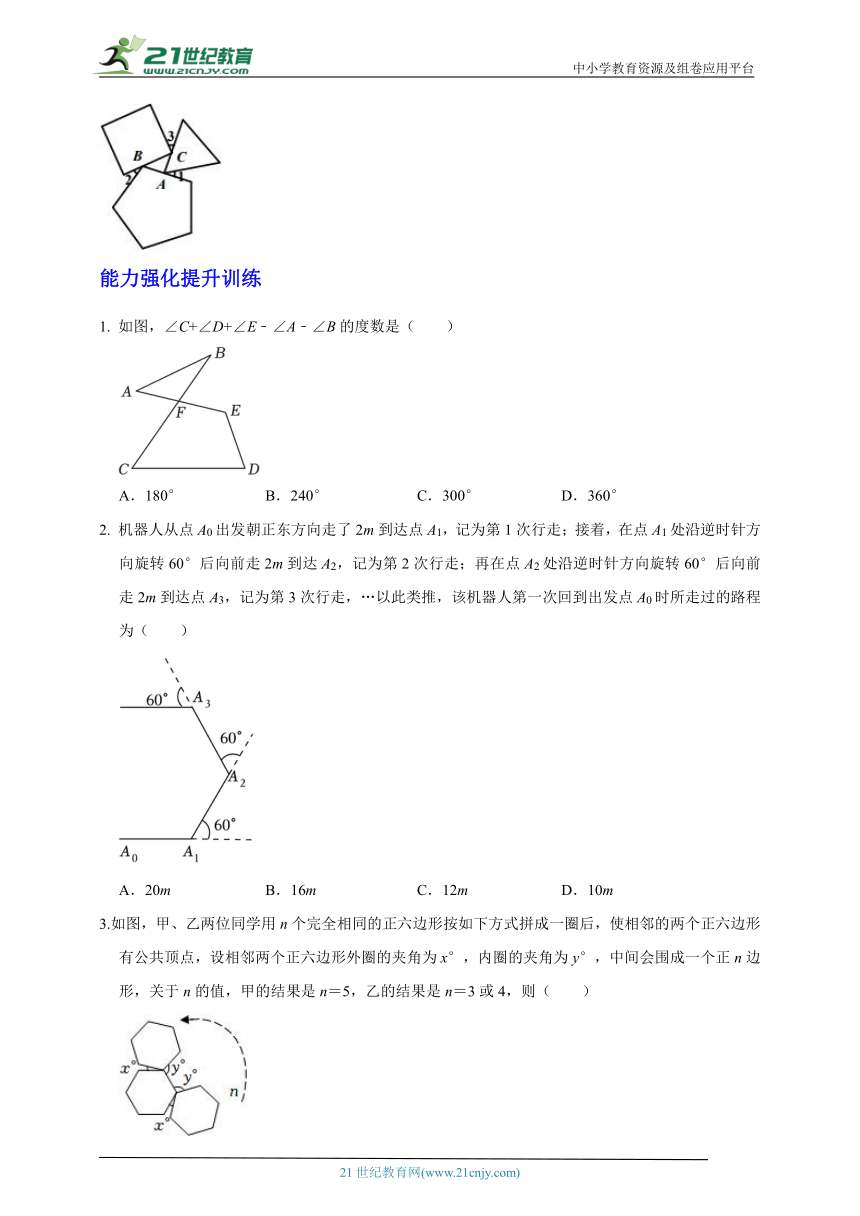
【例2-3】如图,将等边三角形、正方形和正五边形按如图所示的位置摆放.,则=___.
能力强化提升训练
如图,∠C+∠D+∠E﹣∠A﹣∠B的度数是( )
A.180° B.240° C.300° D.360°
机器人从点A0出发朝正东方向走了2m到达点A1,记为第1次行走;接着,在点A1处沿逆时针方向旋转60°后向前走2m到达A2,记为第2次行走;再在点A2处沿逆时针方向旋转60°后向前走2m到达点A3,记为第3次行走,…以此类推,该机器人第一次回到出发点A0时所走过的路程为( )
A.20m B.16m C.12m D.10m
3.如图,甲、乙两位同学用n个完全相同的正六边形按如下方式拼成一圈后,使相邻的两个正六边形有公共顶点,设相邻两个正六边形外圈的夹角为x°,内圈的夹角为y°,中间会围成一个正n边形,关于n的值,甲的结果是n=5,乙的结果是n=3或4,则( )
A.甲的结果正确
B.乙的结果正确
C.甲、乙的结果合在一起才正确
D.甲、乙的结果合在一起也不正确
4.如图,四边形ABCD中,∠C=90°,BE平分∠ABC,BE、CD交于G点.
(1)如图1,若∠A=90°,
①求证:∠EDG=∠ABC;
②作DF平分∠ADC,如图2,求证:DF∥BG.
(2)如图3,作DF平分∠ADC,在锐角∠BAD内部作射线AN,交DF于N,若∠AND﹣∠GBC的大小为45°,试说明:AN平分∠BAD.
堂堂清
一、填空题(每小题4分,共32分)
1.若一个多边形的内角和为540°,则该多边形的边数为( )
A.3 B.4 C.5 D.6
2 .一个多边形的每个内角都等于140°,则这个多边形的边数是( )
A.7 B.8 C.9 D.10
若一个n边形的内角和为900°,则n的值是( )
A.9 B.7 C.6 D.5
正十二边形的外角和为( )
A.30° B.150° C.360° D.1800°
5 .如果一个多边形的每一个外角都等于60°,那么这个多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
6 .如图,以正方形ABCD的边CD向外作正五边形CDEFG,则∠ADE的度数为( )
A.172° B.162° C.152° D.150°
若一个多边形截去一个角后,变成四边形,则原来的多边形的边数可能为( )
A.4或5 B.3或4 C.3或4或5 D.4或5或6
如图,七边形ABCDEFG中,AB,ED的延长线交于点O,若∠1,∠2,∠3,∠4的外角和等于220°,则∠BOD的度数为( )
A.20° B.35° C.40° D.45°
二、填空题(每小题4分,共20分)
9 .在五边形中,,,,则的度数是______.
10 .已知一个多边形被截取一个角后,内角和变为1620°,则原多边形的边数为________.
11 .如图,奇奇先从点A出发前进4m,向右转15°,再前进4m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了___________
A.24m B.48m C.64m D.96m
12 .如图,△ABC 中,,剪去角后,得到一个四边形,则的度数为____________.
13 .如图,已知, _______.
解答题(共6小题,48分)
14 .(6分)已知一个正多边形的每个内角比它的每个外角多60°,求这个多边形的边数.
15 .(8分)如图,已知在四边形中,,.
(1)的度数为___________;
(2)若的平分线交边于点E,且,求的度数.
16 .(8分)小红把一副直角三角板按如图所示的方式摆放在一起,其中,,,,求的度数.
17 .(8分)在一个各内角都相等的多边形中,每一个内角都比相邻外角的倍还大.
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
18 .(8分)阅读并解决下列问题:
(1)如图①,中,,、的平分线交于点D,则______.
(2)如图②,五边形中,,EF平分,平分,若,求的度数.
19 .(10分)阅读材料:
如图1,AB、CD交于点O,我们把△AOD和△BOC叫做对顶三角形.
结论:若△AOD和△BOC是对顶三角形,则∠A+∠D=∠B+∠C.
结论应用举例:
如图2:求五角星的五个内角之和,即∠A+∠B+∠ACE+∠ADB+∠E的度数.
解:连接CD,由对顶三角形的性质得:∠B+∠E=∠1+∠2,
在△ACD中,∵∠A+∠ACD+∠ADC=180°,
即∠A+∠3+∠1+∠2+∠4=180°,
∴∠A+∠ACE+∠B+∠E+ADB=180°
即五角星的五个内角之和为180°.
解决问题:
(1)如图①,∠A+∠B+∠C+∠D+∠E+∠F= ;
(2)如图②,∠A+∠B+∠C+∠D+∠E+∠F+∠G= ;
(3)如图③,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H= ;
(4)如图④,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N= ;
请你从图③或图④中任选一个,写出你的计算过程.
拓展培优*冲刺满分
1 .如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形,如图,就是一组正多边形,观察每个正多边形中∠的变化情况,解答下列问题.
(1)将如表的表格补充完整:
正多边形的边数 3 4 5 6 …… n
∠的度数 ……
(2)根据规律,是否存在一个正n边形,使其中的∠=20°?若存在,求出n的值;若不存在,请说明理由.
2 .如图,在四边形ABCD中,∠ADC=α,∠BCD=β,延长AB到点E,AF是∠DAB的平分线,BG是∠CBE的平分线.
(1)如图1,当AF∥BG时,求证:α+β=180°
(2)如图2,当 α+β>180° 时,直线AF交直线BG于点M,问∠AMB 与α,β之间有何数量关系?写出你的结论并证明;
(3)如果将(2)中的条件 α+β>180° 改为 α+β<180°,那么∠AMB与α,β之间又有何数量关系?请直接写出结论,不用证明.
八年级数学上分层优化堂堂清
十一章 三角形
11.3多边形及其内角和
11.3.2 多边形的内角和(解析版)
学习目标:
1.能通过不同方法探索多边形的内角和与外角和公式.
2.学会运用多边形的内角和与外角和公式解决问题.
老师对你说:
多边形的内角和
多边形的内角和公式:n边形的内角和等于(n-2)×180°。
多边形的内角和推理方法
方法1:如图1所示,从n边形的一个顶点引出(n-3)条对角线,这(n-3)条对角线把n边形分成(n-2)个三角形,每个三角形的内角和是180°,所以n边形的内角和为(n-2)×180°。
方法2:如图2所示,在n边形内任取一点P,连接PA1,PA2……PAn,把n边形分成n个三角形,这n个三角形的内角和为n ×180°,再减去一个周角,即得n边形的内角和为n×180° -360°=(n-2)×180°。
方法3:如图3所示,如图所示,在n边形的 一边上任取一点P与各顶点相连,得(n-1)个三角形,n边形内角和等于这(n-1)个三角形的内角和减去在点P 处的一个平角,即得n边形的内角和为(n-1)×180° -180° =(n-2)×180°。
多边形的外角和
性质:多边形的外角和等于360°。
基础提升 教材核心知识点精练
知识点1:多边形的内角和
【例1-1】一个多边形的内角和为1800°,则这个多边形为( )
A.九边形 B.十边形 C.十一边形 D.十二边形
【答案】D
【解析】
【分析】
根据多边形内角和公式“”进行计算,即可得.
【详解】
解:由题意得,
,
故选D.
【点评】
本题考查了多边形的内角和,解题的关键是掌握多边形内角和公式.
【例1-2】一个多边形的内角和的度数可能是( )
A.2700° B.2800° C.2900° D.3000°
【分析】设多边形的边数为n,利用多边形内角和公式根据各项数值列得方程,解方程判断n的值是否为整数即可.
【解答】解:多边形的边数为n,
(n﹣2) 180°=2700°,
解得:n=17,
则A符合题意;
(n﹣2) 180°=2800°,
此时方程的解不是整数,
则B符合题意;
(n﹣2) 180°=2900°,
此时方程的解不是整数,
则C符合题意;
(n﹣2) 180°=3000°,
此时方程的解不是整数,
则D符合题意;
故选:A.
【点评】本题考查多边形的内角和公式,此为基础且重要知识点,必须熟练掌握.
【例1-3】如图,一束太阳光线平行照射在放置于地面的正六边形上,若,则的度数为( )
A. B. C. D.
【答案】B
【分析】如图,求出正六边形的一个内角和一个外角的度数,得到,平行线的性质,得到,三角形的外角的性质,得到,进而求出的度数.
【详解】解:如图:
∵正六边形的一个外角的度数为:,
∴正六边形的一个内角的度数为:,
即:,
∵一束太阳光线平行照射在放置于地面的正六边形上,,
∴,
∴,
∴;
故选B.
【点评】本题考查正多边形的内角和、外角和的综合应用,平行线的性质.熟练掌握多边形的外角和是,是解题的关键.
知识点2:多边形的外角和
【例2-1】如图,小明从正八边形(各边相等,各内角也相等)草地的一边AB上一点S出发,步行一周回到原处在步行的过程中,小明转过的角度的和是( )
A. B. C. D.
【答案】D
【解析】
【分析】
根据正八边形的内角和求出每个内角,再求出每次转过的角度45°,一共转8次,利用45°×8计算即可.
【详解】
解:∵ABCDEFGH为正八边形,
∴每个内角为(8-2)×180°÷8=135°,
小明每转一次转过的角为180°-135°=45°,
步行一周回到原处,小明一共转八次所有转过的角度之和为45°×8=360°,
故选:D.
【点评】本题考查正八边形的内角和、每个内角、外角与外角和,掌握正多边形相关知识是解题关键
【例2-2】若一个多边形的内角和与外角和之比是的5︰2,则这个多边形的边数是__________.
【答案】7
【解析】
【分析】
设这个多边形的边数是n,则内角和为,然后根据外角和是360度,即可求得边数.
【详解】
解:设这个多边形的边数是n,则
∴
解得;
故答案为:7.
【点睛】
本题考查了多边形的计算,理解多边形的外角和是360度,外角和不随边数的变化而变化是关键.
【例2-3】如图,将等边三角形、正方形和正五边形按如图所示的位置摆放.,则=___.
【答案】##42度
【解析】
【分析】
利用多边形的外角和定理,即减去等边三角形的一个内角的度数,减去正五边形的一个内角的度数,减去正方形的一个内角的度数,再减去和的度数,最后得出答案.
【详解】
等边三角形的内角的度数是,正方形的内角的度数为,正五边形的内角的度数是,
则.
故答案为:
【点评】此题考查了多边形外角和定理,正多边形内角和公式,熟练掌握相关知识及正确运算是解题关键.
能力强化提升训练
如图,∠C+∠D+∠E﹣∠A﹣∠B的度数是( )
A.180° B.240° C.300° D.360°
【分析】根据三角形内角和定理及对顶角相等易得∠A+∠B=180°﹣∠CFE,再利用四边形内角和为360°进行计算即可求得答案.
【解答】解:∵∠A+∠B+∠AFB=180°,∠CFE=∠AFB,
∴∠A+∠B=180°﹣∠CFE
∴∠C+∠D+∠E﹣∠A﹣∠B
=∠C+∠D+∠E﹣(∠A+∠B)
=∠C+∠D+∠E﹣(180°﹣∠CFE)
=∠C+∠D+∠E+∠CFE﹣180°
=360°﹣180°
=180°,
故选:A.
【点评】本题考查多边形的内角和,结合已知条件求得∠A+∠B=180°﹣∠CFE是解题的关键.
机器人从点A0出发朝正东方向走了2m到达点A1,记为第1次行走;接着,在点A1处沿逆时针方向旋转60°后向前走2m到达A2,记为第2次行走;再在点A2处沿逆时针方向旋转60°后向前走2m到达点A3,记为第3次行走,…以此类推,该机器人第一次回到出发点A0时所走过的路程为( )
A.20m B.16m C.12m D.10m
【分析】由题意可知机器人从点A0出发第一次回到A0时所围成的图形是一个正多边形,结合其外角和为360°求得边数后再乘以2即可求得答案.
【解答】解:由题意可知机器人从点A0出发第一次回到A0时所围成的图形是一个正多边形,
则其边数为:360°÷60°=6(条),
那么6×2=12(m),
即该机器人第一次回到出发点A0时所走过的路程为12m,
故选:C.
【点评】本题考查多边形的外角和,由题意得出机器人从点A0出发第一次回到A0时所围成的图形是一个正多边形是解题的关键.
3.如图,甲、乙两位同学用n个完全相同的正六边形按如下方式拼成一圈后,使相邻的两个正六边形有公共顶点,设相邻两个正六边形外圈的夹角为x°,内圈的夹角为y°,中间会围成一个正n边形,关于n的值,甲的结果是n=5,乙的结果是n=3或4,则( )
A.甲的结果正确
B.乙的结果正确
C.甲、乙的结果合在一起才正确
D.甲、乙的结果合在一起也不正确
【分析】正六边形的一个内角为120°,根据周角的定义有,x+y=360°﹣2×120°=120°,得y,再讨论即可得n的值.
【解答】解:∵正六边形的一个内角为120°,
∴x+y=360°﹣2×120°=120°,
∵y°为正n边形的一个内角为度数,
∴y,
当n=3时,y=60°,则x=60°,
当n=4时,y=90°,则x=30°,
当n=5时,y=108°,则x=12°,
当n=6时,y=120°,x=0°,
则n的值为3或4或5或6.
故选:D.
【点评】本题考查了多边形的内角与外角.注意求正多边形的内角常常转化到求外角来计算.
4.如图,四边形ABCD中,∠C=90°,BE平分∠ABC,BE、CD交于G点.
(1)如图1,若∠A=90°,
①求证:∠EDG=∠ABC;
②作DF平分∠ADC,如图2,求证:DF∥BG.
(2)如图3,作DF平分∠ADC,在锐角∠BAD内部作射线AN,交DF于N,若∠AND﹣∠GBC的大小为45°,试说明:AN平分∠BAD.
【分析】(1)①根据四边形内角和得出∠ABC+∠ADC=360°﹣90°﹣90°=180°,根据邻补角得出∠EDG+∠ADC=180°,根据补角的性质即可得出结论;
②根据角平分线的定义结合∠ABC+∠ADC=180°,得出,根据∠DFC+∠4=90°,得出∠2=∠DFC,根据平行线的判定得出DF∥BG;
(2)延长AB、DF交于点M,求出∠DAN=135°﹣∠2﹣∠3,∠BAN=135°﹣∠2﹣∠3,证明∠DAN=∠BAN,即可证明AN平分∠BAD.
【解答】证明:(1)①∵∠C=90°,∠A=90°,
∴∠ABC+∠ADC=360°﹣90°﹣90°=180°,
∵∠EDG+∠ADC=180°,
∴∠EDG=∠ABC;
②∵BE平分∠ABC,
∴,
∵DF平分∠ADC,
∴,
∴,
∵∠C=90°,
∴∠DFC+∠4=90°,
∴∠2=∠DFC,
∴DF∥BG;
(2)延长AB、DF交于点M,如图所示:
∵∠AND﹣∠GBC=45°,
∴∠AND=∠2+45°,
∴∠DAN=180°﹣∠AND﹣∠3
=180°﹣∠2﹣45°﹣∠3
=135°﹣∠2﹣∠3,
∵BE平分∠ABC,
∴,
∵DF平分∠ADC,
∴,
∵∠BFM=∠CFD=90°﹣∠4=90°﹣∠3,
∴∠AMN=∠ABC﹣∠BFM=2∠2﹣90°+∠3,
∴∠BAN=∠AND﹣∠AMN
=45°+∠2﹣2∠2+90°﹣∠3
=135°﹣∠2﹣∠3,
∴∠DAN=∠BAN,
∴AN平分∠BAD.
【点评】本题主要考查了角平分线的定义,平行线的判定,补角和余角的性质,三角形外角的性质,三角形内角和定理,解题的关键是作出辅助线,数形结合.
堂堂清
一、填空题(每小题4分,共32分)
1.若一个多边形的内角和为540°,则该多边形的边数为( )
A.3 B.4 C.5 D.6
【答案】C
【解答】解:由多边形的内角和公式可得,
(n﹣2)×180°=540°,
解得:n=5,
故选:C.
2 .一个多边形的每个内角都等于140°,则这个多边形的边数是( )
A.7 B.8 C.9 D.10
【答案】C
【解答】解:由题意可得:180° (n﹣2)=140° n,
解得n=9,
故多边形是九边形.
故选:C.
若一个n边形的内角和为900°,则n的值是( )
A.9 B.7 C.6 D.5
【答案】B
【解答】解:这个多边形的边数是n,
则(n﹣2) 180°=900°,
解得:n=7.
故选:B.
正十二边形的外角和为( )
A.30° B.150° C.360° D.1800°
【答案】C
【解答】解:因为多边形的外角和为360°,所以正十二边形的外角和为:360°.故选:C.
5 .如果一个多边形的每一个外角都等于60°,那么这个多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
【答案】A
【解答】解:360°÷60°=6,
∴这个多边形是六边形.
故选:A.
6 .如图,以正方形ABCD的边CD向外作正五边形CDEFG,则∠ADE的度数为( )
A.172° B.162° C.152° D.150°
【答案】B
【解答】解:∵五边形CDEFG为正五边形,
∴∠CDE=(5﹣2)×180°÷5=108°,
∵正方形ABCD中,∠ADC=90°,
∴∠ADE=360°﹣∠ADC﹣∠CDE=360°﹣90°﹣108°=162°,
故选:B
若一个多边形截去一个角后,变成四边形,则原来的多边形的边数可能为( )
A.4或5 B.3或4 C.3或4或5 D.4或5或6
【答案】C
【解答】解:当多边形是五边形时,截去一个角时,可能变成四边形;
当多边形是四边形时,截去一个角时,可能变成四边形;
当多边形是三角形时,截去一个角时,可能变成四边形;
所以原来的多边形的边数可能为:3或4或5.
故选:C.
如图,七边形ABCDEFG中,AB,ED的延长线交于点O,若∠1,∠2,∠3,∠4的外角和等于220°,则∠BOD的度数为( )
A.20° B.35° C.40° D.45°
【答案】C
【解答】解:∵∠1、∠2、∠3、∠4的外角和等于220°,五边形AOEFG的外角和为360°,
∴∠BOD的外角为 360°﹣220°=140°,
∴∠BOD=180°﹣140°=40°,
故选:C.
二、填空题(每小题4分,共20分)
9 .在五边形中,,,,则的度数是______.
【答案】##142度
【解析】
【分析】
根据平行线的性质求得根据,可得,根据,以及五边形的内角和为,即可求解.
【详解】
,
,
,
五边形的内角和为,,
.
故答案为:.
【点评】本题考查了平行线的性质,垂线的定义,多边形的内角和,掌握以上知识是解题的关键.
10 .已知一个多边形被截取一个角后,内角和变为1620°,则原多边形的边数为________.
【答案】10或11或12
【分析】根据多边形的内角和公式,先计算出截取之后的边数,再进行分类讨论即可.
【详解】解:设截取后多边形的边数为n,
,解得:,
,.
故答案为:10或11或12.
【点评】本题主要考查了多边形的内角和,解题的关键是掌握多边形的内角和公式以及掌握一个多边形截取一个角后边的数量可能会增加一条,可能不变,也可能减少一条.
11 .如图,奇奇先从点A出发前进4m,向右转15°,再前进4m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了___________
A.24m B.48m C.64m D.96m
【答案】96
【解答】解:∵奇奇从A点出发最后回到出发点A时正好走了一个正多边形,
∴根据外角和定理可知正多边形的边数为n=360°÷15°=24,
则一共走了24×4=96(米).
12 .如图,△ABC 中,,剪去角后,得到一个四边形,则的度数为____________.
【答案】260°
【分析】根据四边形内角和为360°,得出∠1+∠2=360°-(∠B+∠C),根据∠A=80°,得出∠B+∠C=180°-∠A=100°,即可得出答案.
【详解】解:∵四边形内角和为360°,
∴∠1+∠2=360°-∠B-∠C=360°-(∠B+∠C)
∵∠A=80°,
∴∠B+∠C=180°-∠A=100°,
∴∠1+∠2=360°-100°=260°,
故答案为:260°.
【点评】本题考查了多边形内角和,掌握知识点是解题关键.
13 .如图,已知, _______.
【答案】/240度
【分析】由三角形的外角性质和三角形内角和定理即可得出结果.
【详解】连接,,
∴
又,
∴
.
故答案为:.
【点评】本题考查了三角形的外角性质、对顶角相等以及三角形内角和定理;熟练掌握三角形的外角性质以及三角形内角和定理是解决问题的关键.
解答题(共6小题,48分)
14 .(6分)已知一个正多边形的每个内角比它的每个外角多60°,求这个多边形的边数.
【答案】6
【分析】设内角为x°,则外角为(x﹣60)°,根据内角与外角互补可列方程求出内角度数,进而可求出外角,再利用多边形外角和为360°即可求出边数.
【详解】解:设内角为x°,则外角为(x﹣60)°,由题意得:
x+x﹣60=180,
解得:x=120,
则外角为120°﹣60°=60°,
多边形的边数:360°÷60°=6.
【点评】此题主要考查了多边形的内角与外角,关键是掌握内角与相邻外角和为180°.
15 .(8分)如图,已知在四边形中,,.
(1)的度数为___________;
(2)若的平分线交边于点E,且,求的度数.
【答案】(1)(2)
【解析】
【分析】
(1)根据四边形的内角和求解即可;
(2)根据平行线的性质,求出∠BCE的度数,根据,求出∠BCD的度数,即可得出∠D的度数.
(1)
∵在四边形ABCD中,∠A=70°,∠B=140°,
∴∠BCD+∠D=
;
故答案为:150°;
(2)
,
,
,
,
平分∠BCD,
,
.
【点评】本题主要考查了四边形的内角和,角平分线的定义和平行线的性质,熟练掌握平行线的性质是解题的关键.
16 .(8分)小红把一副直角三角板按如图所示的方式摆放在一起,其中,,,,求的度数.
【答案】
【解析】
【分析】
如图,由三角形的外角的性质可得: 可得 再利用三角形的内角和求解 再利用四边形的内角和求解 再求解 从而可得结论.
【详解】
解:如图,由三角形的外角的性质可得:
【点评】本题考查的是三角形的内角和,四边形的内角和定理,三角形的外角的性质,平角的定义,掌握以上知识是解题的关键.
17 .(8分)在一个各内角都相等的多边形中,每一个内角都比相邻外角的倍还大.
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
【答案】(1)9;(2)1080 或1260 或1440 .
【解析】
【分析】
(1)设多边形的一个外角为,则与其相邻的内角等于,根据内角与其相邻的外角的和是 列出方程,求出的值,再由多边形的外角和为,求出此多边形的边数为;
(2)剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,根据多边形的内角和定理即可求出答案.
【详解】
解:(1)设每一个外角为,则与其相邻的内角等于,
,
,即多边形的每个外角为,
∵多边形的外角和为,
∴多边形的外角个数为:,
∴这个多边形的边数为;
(2)因为剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,
①若剪去一角后边数减少1条,即变成边形,
内角和为,
②若剪去一角后边数不变,即变成边形,
内角和为,
③若剪去一角后边数增加1,即变成边形,
内角和为,
∴将这个多边形剪去一个角后,剩下多边形的内角和为或或 .
【点评】本题考查了多边形的内角和定理,外角和定理,多边形内角与外角的关系,熟练掌握相关知识点是解题的关键.
18 .(8分)阅读并解决下列问题:
(1)如图①,中,,、的平分线交于点D,则______.
(2)如图②,五边形中,,EF平分,平分,若,求的度数.
图① 图②
【答案】(1);(2)
【解析】
【分析】
(1)先根据三角形内角和及角平分线求出,然后再根据三角形内角和求出的度数即可.
(2)首先根据得出,然后根据五边形内角和求出,由角平分线的性质进而得出,再根据四边形内角和即可求出的度数.
【详解】
(1),分别平分、,
,,
,
,
,
,
.
(2)∵EF平分,CF平分,
设,,
∵,
∴,
∵五边形的内角和为,
∴,
即,
∴,
∵,
∴.
【点评】本题考查了多边形的内角和、平行线的性质及角平分线的性质,解题的关键是熟练掌握多边形内角和的求法及灵活运用角平分线的性质.
19 .(10分)阅读材料:
如图1,AB、CD交于点O,我们把△AOD和△BOC叫做对顶三角形.
结论:若△AOD和△BOC是对顶三角形,则∠A+∠D=∠B+∠C.
结论应用举例:
如图2:求五角星的五个内角之和,即∠A+∠B+∠ACE+∠ADB+∠E的度数.
解:连接CD,由对顶三角形的性质得:∠B+∠E=∠1+∠2,
在△ACD中,∵∠A+∠ACD+∠ADC=180°,
即∠A+∠3+∠1+∠2+∠4=180°,
∴∠A+∠ACE+∠B+∠E+ADB=180°
即五角星的五个内角之和为180°.
解决问题:
(1)如图①,∠A+∠B+∠C+∠D+∠E+∠F= ;
(2)如图②,∠A+∠B+∠C+∠D+∠E+∠F+∠G= ;
(3)如图③,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H= ;
(4)如图④,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N= ;
请你从图③或图④中任选一个,写出你的计算过程.
【答案】(1)360°;(2)540°;(3)720°;(4)1080°;过程见解析
【解析】
【分析】
(1)连接CD,由对顶角三角形可得∠A+∠B=∠BDC+∠ACD,再由四边形的内角和定理得出结论;
(2)连接ED,由对顶角三角形可得∠A+∠B=∠BED+∠ADE,再由五边形的内角和定理得出结论;
(3)连接BH、DE,由对顶角三角形可知∠EBH+∠BHD=∠HDE+∠BED,再根据五边形的内角和定理得出结论;
(4)连接ND、NE,由对顶角三角形可知∠1+∠2=∠NGH+∠EHG,再由六边形的内角和定理得出结论.
【详解】
解:(1)连接CD,由对顶角三角形可得∠A+∠B=∠BDC+∠ACD,则∠A+∠B+∠C+∠D+∠E+∠F=360°;
(2)连接ED,由对顶角三角形可得∠A+∠B=∠BED+∠ADE,则∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°;
(3)连接BH、DE,
∵由对顶角三角形可知∠EBH+∠BHD=∠HDE+∠BED,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=五边形CDEFG的内角和+△ABH的内角和=540°+180°=720°;
(4)连接ND、NE,
∵由对顶角三角形可知∠1+∠2=∠NGH+∠EHG,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=六边形BCFGHM的内角和+△AND的内角和+△NDE的内角和=(6-2)×180°+360°=1080°.
故答案为:360°;540°;720°;1080°.
【点评】本题考查的是三角形内角和定理,根据题意作出辅助线,利用△AOD和△BOC叫做对顶三角形的性质及多边形的内角和定理解答是解答此题的关键.
拓展培优*冲刺满分
1 .如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形,如图,就是一组正多边形,观察每个正多边形中∠的变化情况,解答下列问题.
(1)将如表的表格补充完整:
正多边形的边数 3 4 5 6 …… n
∠的度数 ……
(2)根据规律,是否存在一个正n边形,使其中的∠=20°?若存在,求出n的值;若不存在,请说明理由.
【答案】(1),,,,;(2)存在,
【解析】
【分析】
(1)根据计算、观察,可发现规律:正n边形中的∠α=;
(2)根据正n边形中的∠α=,可得答案.
【详解】
解:(1)观察上面每个正多边形中的,填写下表:
正多边形边数 3 4 5 6
的度数
故答案为:,,,,;
(2)存在,理由如下:
设存在正边形使得,
得.
解得:,
存在正边形使得.
【点睛】
本题考查了多边形内角与外角,每题都利用了正多边形的内角:,三角形的内角和定理,等腰三角形的两底角相等.
2 .如图,在四边形ABCD中,∠ADC=α,∠BCD=β,延长AB到点E,AF是∠DAB的平分线,BG是∠CBE的平分线.
(1)如图1,当AF∥BG时,求证:α+β=180°
(2)如图2,当 α+β>180° 时,直线AF交直线BG于点M,问∠AMB 与α,β之间有何数量关系?写出你的结论并证明;
(3)如果将(2)中的条件 α+β>180° 改为 α+β<180°,那么∠AMB与α,β之间又有何数量关系?请直接写出结论,不用证明.
【分析】(1)AF是∠DAB的平分线,BG是∠CBE的平分线,得∠BAD=2∠BAF,∠EBC=2∠EBG,由AF∥BG,得∠BAF=∠EBG,所以∠BAD=∠EBC,则AD∥BC,所以α+β=180°;
(2)延长AD、BC交于点H,由∠EBM∠EBC,∠BAM∠BAD,得∠AMB=∠EBM﹣∠BAM(∠EBC﹣∠BAD)∠H,则2∠AMB=∠H=180°﹣(∠HDC+∠HCD)=180°﹣(180°﹣α+180°﹣β)=α+β﹣180°;
(3)延长DA、CB交于点L,由∠ABM=∠EBG∠EBC∠ABL,∠BAF∠BAD,得∠AMB=∠BAF﹣∠ABM(∠BAD﹣∠ABL)∠L,则2∠AMB=∠L=180°﹣α﹣β.
【解答】(1)证明:∵AF是∠DAB的平分线,BG是∠CBE的平分线,
∴∠BAD=2∠BAF,∠EBC=2∠EBG,
∴AF∥BG,
∴∠BAF=∠EBG,
∴2∠BAF=2∠EBG,
∴∠BAD=∠EBC,
∴AD∥BC,
∴α+β=180°.
(2)解:2∠AMB=α+β﹣180°,
证明:如图2,延长AD、BC交于点H,
∵∠EBM∠EBC,∠BAM∠BAD,
∴∠AMB=∠EBM﹣∠BAM(∠EBC﹣∠BAD)∠H,
∴2∠AMB=∠H,
∵∠H=180°﹣(∠HDC+∠HCD)=180°﹣(180°﹣α+180°﹣β)=α+β﹣180°,
∴2∠AMB=α+β﹣180°.
(3)2∠AMB=180°﹣α﹣β,
证明:如图3,α+β<180°,延长DA、CB交于点L,
∵∠ABM=∠EBG,∠EBC=∠ABL,
∴∠ABM=∠EBG∠EBC∠ABL,
∵∠BAF∠BAD,
∴∠AMB=∠BAF﹣∠ABM(∠BAD﹣∠ABL)∠L,
∴2∠AMB=∠L,
∵∠L=180°﹣α﹣β,
∴2∠AMB=180°﹣α﹣β.
【点评】此题重点考查角平行线的性质、平分线的定义、三角形的内角和等于180°、三角形的一个外角等于与它不相邻的两个内角的和等知识,正确地作出所需要的辅助线是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
八年级数学上分层优化堂堂清
十一章 三角形
11.3多边形及其内角和
11.3.2 多边形的内角和
学习目标:
1.能通过不同方法探索多边形的内角和与外角和公式.
2.学会运用多边形的内角和与外角和公式解决问题.
老师对你说:
多边形的内角和
多边形的内角和公式:n边形的内角和等于(n-2)×180°。
多边形的内角和推理方法
方法1:如图1所示,从n边形的一个顶点引出(n-3)条对角线,这(n-3)条对角线把n边形分成(n-2)个三角形,每个三角形的内角和是180°,所以n边形的内角和为(n-2)×180°。
方法2:如图2所示,在n边形内任取一点P,连接PA1,PA2……PAn,把n边形分成n个三角形,这n个三角形的内角和为n ×180°,再减去一个周角,即得n边形的内角和为n×180° -360°=(n-2)×180°。
方法3:如图3所示,如图所示,在n边形的 一边上任取一点P与各顶点相连,得(n-1)个三角形,n边形内角和等于这(n-1)个三角形的内角和减去在点P 处的一个平角,即得n边形的内角和为(n-1)×180° -180° =(n-2)×180°。
多边形的外角和
性质:多边形的外角和等于360°。
基础提升 教材核心知识点精练
知识点1:多边形的内角和
【例1-1】一个多边形的内角和为1800°,则这个多边形为( )
A.九边形 B.十边形 C.十一边形 D.十二边形
【例1-2】一个多边形的内角和的度数可能是( )
A.2700° B.2800° C.2900° D.3000°
【例1-3】如图,一束太阳光线平行照射在放置于地面的正六边形上,若,则的度数为( )
A. B. C. D.
知识点2:多边形的外角和
【例2-1】如图,小明从正八边形(各边相等,各内角也相等)草地的一边AB上一点S出发,步行一周回到原处在步行的过程中,小明转过的角度的和是( )
A. B. C. D.
【例2-2】若一个多边形的内角和与外角和之比是的5︰2,则这个多边形的边数是__________.
【例2-3】如图,将等边三角形、正方形和正五边形按如图所示的位置摆放.,则=___.
能力强化提升训练
如图,∠C+∠D+∠E﹣∠A﹣∠B的度数是( )
A.180° B.240° C.300° D.360°
机器人从点A0出发朝正东方向走了2m到达点A1,记为第1次行走;接着,在点A1处沿逆时针方向旋转60°后向前走2m到达A2,记为第2次行走;再在点A2处沿逆时针方向旋转60°后向前走2m到达点A3,记为第3次行走,…以此类推,该机器人第一次回到出发点A0时所走过的路程为( )
A.20m B.16m C.12m D.10m
3.如图,甲、乙两位同学用n个完全相同的正六边形按如下方式拼成一圈后,使相邻的两个正六边形有公共顶点,设相邻两个正六边形外圈的夹角为x°,内圈的夹角为y°,中间会围成一个正n边形,关于n的值,甲的结果是n=5,乙的结果是n=3或4,则( )
A.甲的结果正确
B.乙的结果正确
C.甲、乙的结果合在一起才正确
D.甲、乙的结果合在一起也不正确
4.如图,四边形ABCD中,∠C=90°,BE平分∠ABC,BE、CD交于G点.
(1)如图1,若∠A=90°,
①求证:∠EDG=∠ABC;
②作DF平分∠ADC,如图2,求证:DF∥BG.
(2)如图3,作DF平分∠ADC,在锐角∠BAD内部作射线AN,交DF于N,若∠AND﹣∠GBC的大小为45°,试说明:AN平分∠BAD.
堂堂清
一、填空题(每小题4分,共32分)
1.若一个多边形的内角和为540°,则该多边形的边数为( )
A.3 B.4 C.5 D.6
2 .一个多边形的每个内角都等于140°,则这个多边形的边数是( )
A.7 B.8 C.9 D.10
若一个n边形的内角和为900°,则n的值是( )
A.9 B.7 C.6 D.5
正十二边形的外角和为( )
A.30° B.150° C.360° D.1800°
5 .如果一个多边形的每一个外角都等于60°,那么这个多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
6 .如图,以正方形ABCD的边CD向外作正五边形CDEFG,则∠ADE的度数为( )
A.172° B.162° C.152° D.150°
若一个多边形截去一个角后,变成四边形,则原来的多边形的边数可能为( )
A.4或5 B.3或4 C.3或4或5 D.4或5或6
如图,七边形ABCDEFG中,AB,ED的延长线交于点O,若∠1,∠2,∠3,∠4的外角和等于220°,则∠BOD的度数为( )
A.20° B.35° C.40° D.45°
二、填空题(每小题4分,共20分)
9 .在五边形中,,,,则的度数是______.
10 .已知一个多边形被截取一个角后,内角和变为1620°,则原多边形的边数为________.
11 .如图,奇奇先从点A出发前进4m,向右转15°,再前进4m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了___________
A.24m B.48m C.64m D.96m
12 .如图,△ABC 中,,剪去角后,得到一个四边形,则的度数为____________.
13 .如图,已知, _______.
解答题(共6小题,48分)
14 .(6分)已知一个正多边形的每个内角比它的每个外角多60°,求这个多边形的边数.
15 .(8分)如图,已知在四边形中,,.
(1)的度数为___________;
(2)若的平分线交边于点E,且,求的度数.
16 .(8分)小红把一副直角三角板按如图所示的方式摆放在一起,其中,,,,求的度数.
17 .(8分)在一个各内角都相等的多边形中,每一个内角都比相邻外角的倍还大.
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
18 .(8分)阅读并解决下列问题:
(1)如图①,中,,、的平分线交于点D,则______.
(2)如图②,五边形中,,EF平分,平分,若,求的度数.
19 .(10分)阅读材料:
如图1,AB、CD交于点O,我们把△AOD和△BOC叫做对顶三角形.
结论:若△AOD和△BOC是对顶三角形,则∠A+∠D=∠B+∠C.
结论应用举例:
如图2:求五角星的五个内角之和,即∠A+∠B+∠ACE+∠ADB+∠E的度数.
解:连接CD,由对顶三角形的性质得:∠B+∠E=∠1+∠2,
在△ACD中,∵∠A+∠ACD+∠ADC=180°,
即∠A+∠3+∠1+∠2+∠4=180°,
∴∠A+∠ACE+∠B+∠E+ADB=180°
即五角星的五个内角之和为180°.
解决问题:
(1)如图①,∠A+∠B+∠C+∠D+∠E+∠F= ;
(2)如图②,∠A+∠B+∠C+∠D+∠E+∠F+∠G= ;
(3)如图③,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H= ;
(4)如图④,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N= ;
请你从图③或图④中任选一个,写出你的计算过程.
拓展培优*冲刺满分
1 .如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形,如图,就是一组正多边形,观察每个正多边形中∠的变化情况,解答下列问题.
(1)将如表的表格补充完整:
正多边形的边数 3 4 5 6 …… n
∠的度数 ……
(2)根据规律,是否存在一个正n边形,使其中的∠=20°?若存在,求出n的值;若不存在,请说明理由.
2 .如图,在四边形ABCD中,∠ADC=α,∠BCD=β,延长AB到点E,AF是∠DAB的平分线,BG是∠CBE的平分线.
(1)如图1,当AF∥BG时,求证:α+β=180°
(2)如图2,当 α+β>180° 时,直线AF交直线BG于点M,问∠AMB 与α,β之间有何数量关系?写出你的结论并证明;
(3)如果将(2)中的条件 α+β>180° 改为 α+β<180°,那么∠AMB与α,β之间又有何数量关系?请直接写出结论,不用证明.
八年级数学上分层优化堂堂清
十一章 三角形
11.3多边形及其内角和
11.3.2 多边形的内角和(解析版)
学习目标:
1.能通过不同方法探索多边形的内角和与外角和公式.
2.学会运用多边形的内角和与外角和公式解决问题.
老师对你说:
多边形的内角和
多边形的内角和公式:n边形的内角和等于(n-2)×180°。
多边形的内角和推理方法
方法1:如图1所示,从n边形的一个顶点引出(n-3)条对角线,这(n-3)条对角线把n边形分成(n-2)个三角形,每个三角形的内角和是180°,所以n边形的内角和为(n-2)×180°。
方法2:如图2所示,在n边形内任取一点P,连接PA1,PA2……PAn,把n边形分成n个三角形,这n个三角形的内角和为n ×180°,再减去一个周角,即得n边形的内角和为n×180° -360°=(n-2)×180°。
方法3:如图3所示,如图所示,在n边形的 一边上任取一点P与各顶点相连,得(n-1)个三角形,n边形内角和等于这(n-1)个三角形的内角和减去在点P 处的一个平角,即得n边形的内角和为(n-1)×180° -180° =(n-2)×180°。
多边形的外角和
性质:多边形的外角和等于360°。
基础提升 教材核心知识点精练
知识点1:多边形的内角和
【例1-1】一个多边形的内角和为1800°,则这个多边形为( )
A.九边形 B.十边形 C.十一边形 D.十二边形
【答案】D
【解析】
【分析】
根据多边形内角和公式“”进行计算,即可得.
【详解】
解:由题意得,
,
故选D.
【点评】
本题考查了多边形的内角和,解题的关键是掌握多边形内角和公式.
【例1-2】一个多边形的内角和的度数可能是( )
A.2700° B.2800° C.2900° D.3000°
【分析】设多边形的边数为n,利用多边形内角和公式根据各项数值列得方程,解方程判断n的值是否为整数即可.
【解答】解:多边形的边数为n,
(n﹣2) 180°=2700°,
解得:n=17,
则A符合题意;
(n﹣2) 180°=2800°,
此时方程的解不是整数,
则B符合题意;
(n﹣2) 180°=2900°,
此时方程的解不是整数,
则C符合题意;
(n﹣2) 180°=3000°,
此时方程的解不是整数,
则D符合题意;
故选:A.
【点评】本题考查多边形的内角和公式,此为基础且重要知识点,必须熟练掌握.
【例1-3】如图,一束太阳光线平行照射在放置于地面的正六边形上,若,则的度数为( )
A. B. C. D.
【答案】B
【分析】如图,求出正六边形的一个内角和一个外角的度数,得到,平行线的性质,得到,三角形的外角的性质,得到,进而求出的度数.
【详解】解:如图:
∵正六边形的一个外角的度数为:,
∴正六边形的一个内角的度数为:,
即:,
∵一束太阳光线平行照射在放置于地面的正六边形上,,
∴,
∴,
∴;
故选B.
【点评】本题考查正多边形的内角和、外角和的综合应用,平行线的性质.熟练掌握多边形的外角和是,是解题的关键.
知识点2:多边形的外角和
【例2-1】如图,小明从正八边形(各边相等,各内角也相等)草地的一边AB上一点S出发,步行一周回到原处在步行的过程中,小明转过的角度的和是( )
A. B. C. D.
【答案】D
【解析】
【分析】
根据正八边形的内角和求出每个内角,再求出每次转过的角度45°,一共转8次,利用45°×8计算即可.
【详解】
解:∵ABCDEFGH为正八边形,
∴每个内角为(8-2)×180°÷8=135°,
小明每转一次转过的角为180°-135°=45°,
步行一周回到原处,小明一共转八次所有转过的角度之和为45°×8=360°,
故选:D.
【点评】本题考查正八边形的内角和、每个内角、外角与外角和,掌握正多边形相关知识是解题关键
【例2-2】若一个多边形的内角和与外角和之比是的5︰2,则这个多边形的边数是__________.
【答案】7
【解析】
【分析】
设这个多边形的边数是n,则内角和为,然后根据外角和是360度,即可求得边数.
【详解】
解:设这个多边形的边数是n,则
∴
解得;
故答案为:7.
【点睛】
本题考查了多边形的计算,理解多边形的外角和是360度,外角和不随边数的变化而变化是关键.
【例2-3】如图,将等边三角形、正方形和正五边形按如图所示的位置摆放.,则=___.
【答案】##42度
【解析】
【分析】
利用多边形的外角和定理,即减去等边三角形的一个内角的度数,减去正五边形的一个内角的度数,减去正方形的一个内角的度数,再减去和的度数,最后得出答案.
【详解】
等边三角形的内角的度数是,正方形的内角的度数为,正五边形的内角的度数是,
则.
故答案为:
【点评】此题考查了多边形外角和定理,正多边形内角和公式,熟练掌握相关知识及正确运算是解题关键.
能力强化提升训练
如图,∠C+∠D+∠E﹣∠A﹣∠B的度数是( )
A.180° B.240° C.300° D.360°
【分析】根据三角形内角和定理及对顶角相等易得∠A+∠B=180°﹣∠CFE,再利用四边形内角和为360°进行计算即可求得答案.
【解答】解:∵∠A+∠B+∠AFB=180°,∠CFE=∠AFB,
∴∠A+∠B=180°﹣∠CFE
∴∠C+∠D+∠E﹣∠A﹣∠B
=∠C+∠D+∠E﹣(∠A+∠B)
=∠C+∠D+∠E﹣(180°﹣∠CFE)
=∠C+∠D+∠E+∠CFE﹣180°
=360°﹣180°
=180°,
故选:A.
【点评】本题考查多边形的内角和,结合已知条件求得∠A+∠B=180°﹣∠CFE是解题的关键.
机器人从点A0出发朝正东方向走了2m到达点A1,记为第1次行走;接着,在点A1处沿逆时针方向旋转60°后向前走2m到达A2,记为第2次行走;再在点A2处沿逆时针方向旋转60°后向前走2m到达点A3,记为第3次行走,…以此类推,该机器人第一次回到出发点A0时所走过的路程为( )
A.20m B.16m C.12m D.10m
【分析】由题意可知机器人从点A0出发第一次回到A0时所围成的图形是一个正多边形,结合其外角和为360°求得边数后再乘以2即可求得答案.
【解答】解:由题意可知机器人从点A0出发第一次回到A0时所围成的图形是一个正多边形,
则其边数为:360°÷60°=6(条),
那么6×2=12(m),
即该机器人第一次回到出发点A0时所走过的路程为12m,
故选:C.
【点评】本题考查多边形的外角和,由题意得出机器人从点A0出发第一次回到A0时所围成的图形是一个正多边形是解题的关键.
3.如图,甲、乙两位同学用n个完全相同的正六边形按如下方式拼成一圈后,使相邻的两个正六边形有公共顶点,设相邻两个正六边形外圈的夹角为x°,内圈的夹角为y°,中间会围成一个正n边形,关于n的值,甲的结果是n=5,乙的结果是n=3或4,则( )
A.甲的结果正确
B.乙的结果正确
C.甲、乙的结果合在一起才正确
D.甲、乙的结果合在一起也不正确
【分析】正六边形的一个内角为120°,根据周角的定义有,x+y=360°﹣2×120°=120°,得y,再讨论即可得n的值.
【解答】解:∵正六边形的一个内角为120°,
∴x+y=360°﹣2×120°=120°,
∵y°为正n边形的一个内角为度数,
∴y,
当n=3时,y=60°,则x=60°,
当n=4时,y=90°,则x=30°,
当n=5时,y=108°,则x=12°,
当n=6时,y=120°,x=0°,
则n的值为3或4或5或6.
故选:D.
【点评】本题考查了多边形的内角与外角.注意求正多边形的内角常常转化到求外角来计算.
4.如图,四边形ABCD中,∠C=90°,BE平分∠ABC,BE、CD交于G点.
(1)如图1,若∠A=90°,
①求证:∠EDG=∠ABC;
②作DF平分∠ADC,如图2,求证:DF∥BG.
(2)如图3,作DF平分∠ADC,在锐角∠BAD内部作射线AN,交DF于N,若∠AND﹣∠GBC的大小为45°,试说明:AN平分∠BAD.
【分析】(1)①根据四边形内角和得出∠ABC+∠ADC=360°﹣90°﹣90°=180°,根据邻补角得出∠EDG+∠ADC=180°,根据补角的性质即可得出结论;
②根据角平分线的定义结合∠ABC+∠ADC=180°,得出,根据∠DFC+∠4=90°,得出∠2=∠DFC,根据平行线的判定得出DF∥BG;
(2)延长AB、DF交于点M,求出∠DAN=135°﹣∠2﹣∠3,∠BAN=135°﹣∠2﹣∠3,证明∠DAN=∠BAN,即可证明AN平分∠BAD.
【解答】证明:(1)①∵∠C=90°,∠A=90°,
∴∠ABC+∠ADC=360°﹣90°﹣90°=180°,
∵∠EDG+∠ADC=180°,
∴∠EDG=∠ABC;
②∵BE平分∠ABC,
∴,
∵DF平分∠ADC,
∴,
∴,
∵∠C=90°,
∴∠DFC+∠4=90°,
∴∠2=∠DFC,
∴DF∥BG;
(2)延长AB、DF交于点M,如图所示:
∵∠AND﹣∠GBC=45°,
∴∠AND=∠2+45°,
∴∠DAN=180°﹣∠AND﹣∠3
=180°﹣∠2﹣45°﹣∠3
=135°﹣∠2﹣∠3,
∵BE平分∠ABC,
∴,
∵DF平分∠ADC,
∴,
∵∠BFM=∠CFD=90°﹣∠4=90°﹣∠3,
∴∠AMN=∠ABC﹣∠BFM=2∠2﹣90°+∠3,
∴∠BAN=∠AND﹣∠AMN
=45°+∠2﹣2∠2+90°﹣∠3
=135°﹣∠2﹣∠3,
∴∠DAN=∠BAN,
∴AN平分∠BAD.
【点评】本题主要考查了角平分线的定义,平行线的判定,补角和余角的性质,三角形外角的性质,三角形内角和定理,解题的关键是作出辅助线,数形结合.
堂堂清
一、填空题(每小题4分,共32分)
1.若一个多边形的内角和为540°,则该多边形的边数为( )
A.3 B.4 C.5 D.6
【答案】C
【解答】解:由多边形的内角和公式可得,
(n﹣2)×180°=540°,
解得:n=5,
故选:C.
2 .一个多边形的每个内角都等于140°,则这个多边形的边数是( )
A.7 B.8 C.9 D.10
【答案】C
【解答】解:由题意可得:180° (n﹣2)=140° n,
解得n=9,
故多边形是九边形.
故选:C.
若一个n边形的内角和为900°,则n的值是( )
A.9 B.7 C.6 D.5
【答案】B
【解答】解:这个多边形的边数是n,
则(n﹣2) 180°=900°,
解得:n=7.
故选:B.
正十二边形的外角和为( )
A.30° B.150° C.360° D.1800°
【答案】C
【解答】解:因为多边形的外角和为360°,所以正十二边形的外角和为:360°.故选:C.
5 .如果一个多边形的每一个外角都等于60°,那么这个多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
【答案】A
【解答】解:360°÷60°=6,
∴这个多边形是六边形.
故选:A.
6 .如图,以正方形ABCD的边CD向外作正五边形CDEFG,则∠ADE的度数为( )
A.172° B.162° C.152° D.150°
【答案】B
【解答】解:∵五边形CDEFG为正五边形,
∴∠CDE=(5﹣2)×180°÷5=108°,
∵正方形ABCD中,∠ADC=90°,
∴∠ADE=360°﹣∠ADC﹣∠CDE=360°﹣90°﹣108°=162°,
故选:B
若一个多边形截去一个角后,变成四边形,则原来的多边形的边数可能为( )
A.4或5 B.3或4 C.3或4或5 D.4或5或6
【答案】C
【解答】解:当多边形是五边形时,截去一个角时,可能变成四边形;
当多边形是四边形时,截去一个角时,可能变成四边形;
当多边形是三角形时,截去一个角时,可能变成四边形;
所以原来的多边形的边数可能为:3或4或5.
故选:C.
如图,七边形ABCDEFG中,AB,ED的延长线交于点O,若∠1,∠2,∠3,∠4的外角和等于220°,则∠BOD的度数为( )
A.20° B.35° C.40° D.45°
【答案】C
【解答】解:∵∠1、∠2、∠3、∠4的外角和等于220°,五边形AOEFG的外角和为360°,
∴∠BOD的外角为 360°﹣220°=140°,
∴∠BOD=180°﹣140°=40°,
故选:C.
二、填空题(每小题4分,共20分)
9 .在五边形中,,,,则的度数是______.
【答案】##142度
【解析】
【分析】
根据平行线的性质求得根据,可得,根据,以及五边形的内角和为,即可求解.
【详解】
,
,
,
五边形的内角和为,,
.
故答案为:.
【点评】本题考查了平行线的性质,垂线的定义,多边形的内角和,掌握以上知识是解题的关键.
10 .已知一个多边形被截取一个角后,内角和变为1620°,则原多边形的边数为________.
【答案】10或11或12
【分析】根据多边形的内角和公式,先计算出截取之后的边数,再进行分类讨论即可.
【详解】解:设截取后多边形的边数为n,
,解得:,
,.
故答案为:10或11或12.
【点评】本题主要考查了多边形的内角和,解题的关键是掌握多边形的内角和公式以及掌握一个多边形截取一个角后边的数量可能会增加一条,可能不变,也可能减少一条.
11 .如图,奇奇先从点A出发前进4m,向右转15°,再前进4m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了___________
A.24m B.48m C.64m D.96m
【答案】96
【解答】解:∵奇奇从A点出发最后回到出发点A时正好走了一个正多边形,
∴根据外角和定理可知正多边形的边数为n=360°÷15°=24,
则一共走了24×4=96(米).
12 .如图,△ABC 中,,剪去角后,得到一个四边形,则的度数为____________.
【答案】260°
【分析】根据四边形内角和为360°,得出∠1+∠2=360°-(∠B+∠C),根据∠A=80°,得出∠B+∠C=180°-∠A=100°,即可得出答案.
【详解】解:∵四边形内角和为360°,
∴∠1+∠2=360°-∠B-∠C=360°-(∠B+∠C)
∵∠A=80°,
∴∠B+∠C=180°-∠A=100°,
∴∠1+∠2=360°-100°=260°,
故答案为:260°.
【点评】本题考查了多边形内角和,掌握知识点是解题关键.
13 .如图,已知, _______.
【答案】/240度
【分析】由三角形的外角性质和三角形内角和定理即可得出结果.
【详解】连接,,
∴
又,
∴
.
故答案为:.
【点评】本题考查了三角形的外角性质、对顶角相等以及三角形内角和定理;熟练掌握三角形的外角性质以及三角形内角和定理是解决问题的关键.
解答题(共6小题,48分)
14 .(6分)已知一个正多边形的每个内角比它的每个外角多60°,求这个多边形的边数.
【答案】6
【分析】设内角为x°,则外角为(x﹣60)°,根据内角与外角互补可列方程求出内角度数,进而可求出外角,再利用多边形外角和为360°即可求出边数.
【详解】解:设内角为x°,则外角为(x﹣60)°,由题意得:
x+x﹣60=180,
解得:x=120,
则外角为120°﹣60°=60°,
多边形的边数:360°÷60°=6.
【点评】此题主要考查了多边形的内角与外角,关键是掌握内角与相邻外角和为180°.
15 .(8分)如图,已知在四边形中,,.
(1)的度数为___________;
(2)若的平分线交边于点E,且,求的度数.
【答案】(1)(2)
【解析】
【分析】
(1)根据四边形的内角和求解即可;
(2)根据平行线的性质,求出∠BCE的度数,根据,求出∠BCD的度数,即可得出∠D的度数.
(1)
∵在四边形ABCD中,∠A=70°,∠B=140°,
∴∠BCD+∠D=
;
故答案为:150°;
(2)
,
,
,
,
平分∠BCD,
,
.
【点评】本题主要考查了四边形的内角和,角平分线的定义和平行线的性质,熟练掌握平行线的性质是解题的关键.
16 .(8分)小红把一副直角三角板按如图所示的方式摆放在一起,其中,,,,求的度数.
【答案】
【解析】
【分析】
如图,由三角形的外角的性质可得: 可得 再利用三角形的内角和求解 再利用四边形的内角和求解 再求解 从而可得结论.
【详解】
解:如图,由三角形的外角的性质可得:
【点评】本题考查的是三角形的内角和,四边形的内角和定理,三角形的外角的性质,平角的定义,掌握以上知识是解题的关键.
17 .(8分)在一个各内角都相等的多边形中,每一个内角都比相邻外角的倍还大.
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
【答案】(1)9;(2)1080 或1260 或1440 .
【解析】
【分析】
(1)设多边形的一个外角为,则与其相邻的内角等于,根据内角与其相邻的外角的和是 列出方程,求出的值,再由多边形的外角和为,求出此多边形的边数为;
(2)剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,根据多边形的内角和定理即可求出答案.
【详解】
解:(1)设每一个外角为,则与其相邻的内角等于,
,
,即多边形的每个外角为,
∵多边形的外角和为,
∴多边形的外角个数为:,
∴这个多边形的边数为;
(2)因为剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,
①若剪去一角后边数减少1条,即变成边形,
内角和为,
②若剪去一角后边数不变,即变成边形,
内角和为,
③若剪去一角后边数增加1,即变成边形,
内角和为,
∴将这个多边形剪去一个角后,剩下多边形的内角和为或或 .
【点评】本题考查了多边形的内角和定理,外角和定理,多边形内角与外角的关系,熟练掌握相关知识点是解题的关键.
18 .(8分)阅读并解决下列问题:
(1)如图①,中,,、的平分线交于点D,则______.
(2)如图②,五边形中,,EF平分,平分,若,求的度数.
图① 图②
【答案】(1);(2)
【解析】
【分析】
(1)先根据三角形内角和及角平分线求出,然后再根据三角形内角和求出的度数即可.
(2)首先根据得出,然后根据五边形内角和求出,由角平分线的性质进而得出,再根据四边形内角和即可求出的度数.
【详解】
(1),分别平分、,
,,
,
,
,
,
.
(2)∵EF平分,CF平分,
设,,
∵,
∴,
∵五边形的内角和为,
∴,
即,
∴,
∵,
∴.
【点评】本题考查了多边形的内角和、平行线的性质及角平分线的性质,解题的关键是熟练掌握多边形内角和的求法及灵活运用角平分线的性质.
19 .(10分)阅读材料:
如图1,AB、CD交于点O,我们把△AOD和△BOC叫做对顶三角形.
结论:若△AOD和△BOC是对顶三角形,则∠A+∠D=∠B+∠C.
结论应用举例:
如图2:求五角星的五个内角之和,即∠A+∠B+∠ACE+∠ADB+∠E的度数.
解:连接CD,由对顶三角形的性质得:∠B+∠E=∠1+∠2,
在△ACD中,∵∠A+∠ACD+∠ADC=180°,
即∠A+∠3+∠1+∠2+∠4=180°,
∴∠A+∠ACE+∠B+∠E+ADB=180°
即五角星的五个内角之和为180°.
解决问题:
(1)如图①,∠A+∠B+∠C+∠D+∠E+∠F= ;
(2)如图②,∠A+∠B+∠C+∠D+∠E+∠F+∠G= ;
(3)如图③,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H= ;
(4)如图④,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N= ;
请你从图③或图④中任选一个,写出你的计算过程.
【答案】(1)360°;(2)540°;(3)720°;(4)1080°;过程见解析
【解析】
【分析】
(1)连接CD,由对顶角三角形可得∠A+∠B=∠BDC+∠ACD,再由四边形的内角和定理得出结论;
(2)连接ED,由对顶角三角形可得∠A+∠B=∠BED+∠ADE,再由五边形的内角和定理得出结论;
(3)连接BH、DE,由对顶角三角形可知∠EBH+∠BHD=∠HDE+∠BED,再根据五边形的内角和定理得出结论;
(4)连接ND、NE,由对顶角三角形可知∠1+∠2=∠NGH+∠EHG,再由六边形的内角和定理得出结论.
【详解】
解:(1)连接CD,由对顶角三角形可得∠A+∠B=∠BDC+∠ACD,则∠A+∠B+∠C+∠D+∠E+∠F=360°;
(2)连接ED,由对顶角三角形可得∠A+∠B=∠BED+∠ADE,则∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°;
(3)连接BH、DE,
∵由对顶角三角形可知∠EBH+∠BHD=∠HDE+∠BED,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=五边形CDEFG的内角和+△ABH的内角和=540°+180°=720°;
(4)连接ND、NE,
∵由对顶角三角形可知∠1+∠2=∠NGH+∠EHG,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=六边形BCFGHM的内角和+△AND的内角和+△NDE的内角和=(6-2)×180°+360°=1080°.
故答案为:360°;540°;720°;1080°.
【点评】本题考查的是三角形内角和定理,根据题意作出辅助线,利用△AOD和△BOC叫做对顶三角形的性质及多边形的内角和定理解答是解答此题的关键.
拓展培优*冲刺满分
1 .如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形,如图,就是一组正多边形,观察每个正多边形中∠的变化情况,解答下列问题.
(1)将如表的表格补充完整:
正多边形的边数 3 4 5 6 …… n
∠的度数 ……
(2)根据规律,是否存在一个正n边形,使其中的∠=20°?若存在,求出n的值;若不存在,请说明理由.
【答案】(1),,,,;(2)存在,
【解析】
【分析】
(1)根据计算、观察,可发现规律:正n边形中的∠α=;
(2)根据正n边形中的∠α=,可得答案.
【详解】
解:(1)观察上面每个正多边形中的,填写下表:
正多边形边数 3 4 5 6
的度数
故答案为:,,,,;
(2)存在,理由如下:
设存在正边形使得,
得.
解得:,
存在正边形使得.
【点睛】
本题考查了多边形内角与外角,每题都利用了正多边形的内角:,三角形的内角和定理,等腰三角形的两底角相等.
2 .如图,在四边形ABCD中,∠ADC=α,∠BCD=β,延长AB到点E,AF是∠DAB的平分线,BG是∠CBE的平分线.
(1)如图1,当AF∥BG时,求证:α+β=180°
(2)如图2,当 α+β>180° 时,直线AF交直线BG于点M,问∠AMB 与α,β之间有何数量关系?写出你的结论并证明;
(3)如果将(2)中的条件 α+β>180° 改为 α+β<180°,那么∠AMB与α,β之间又有何数量关系?请直接写出结论,不用证明.
【分析】(1)AF是∠DAB的平分线,BG是∠CBE的平分线,得∠BAD=2∠BAF,∠EBC=2∠EBG,由AF∥BG,得∠BAF=∠EBG,所以∠BAD=∠EBC,则AD∥BC,所以α+β=180°;
(2)延长AD、BC交于点H,由∠EBM∠EBC,∠BAM∠BAD,得∠AMB=∠EBM﹣∠BAM(∠EBC﹣∠BAD)∠H,则2∠AMB=∠H=180°﹣(∠HDC+∠HCD)=180°﹣(180°﹣α+180°﹣β)=α+β﹣180°;
(3)延长DA、CB交于点L,由∠ABM=∠EBG∠EBC∠ABL,∠BAF∠BAD,得∠AMB=∠BAF﹣∠ABM(∠BAD﹣∠ABL)∠L,则2∠AMB=∠L=180°﹣α﹣β.
【解答】(1)证明:∵AF是∠DAB的平分线,BG是∠CBE的平分线,
∴∠BAD=2∠BAF,∠EBC=2∠EBG,
∴AF∥BG,
∴∠BAF=∠EBG,
∴2∠BAF=2∠EBG,
∴∠BAD=∠EBC,
∴AD∥BC,
∴α+β=180°.
(2)解:2∠AMB=α+β﹣180°,
证明:如图2,延长AD、BC交于点H,
∵∠EBM∠EBC,∠BAM∠BAD,
∴∠AMB=∠EBM﹣∠BAM(∠EBC﹣∠BAD)∠H,
∴2∠AMB=∠H,
∵∠H=180°﹣(∠HDC+∠HCD)=180°﹣(180°﹣α+180°﹣β)=α+β﹣180°,
∴2∠AMB=α+β﹣180°.
(3)2∠AMB=180°﹣α﹣β,
证明:如图3,α+β<180°,延长DA、CB交于点L,
∵∠ABM=∠EBG,∠EBC=∠ABL,
∴∠ABM=∠EBG∠EBC∠ABL,
∵∠BAF∠BAD,
∴∠AMB=∠BAF﹣∠ABM(∠BAD﹣∠ABL)∠L,
∴2∠AMB=∠L,
∵∠L=180°﹣α﹣β,
∴2∠AMB=180°﹣α﹣β.
【点评】此题重点考查角平行线的性质、平分线的定义、三角形的内角和等于180°、三角形的一个外角等于与它不相邻的两个内角的和等知识,正确地作出所需要的辅助线是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
