八年级数学上分层优化堂堂清(11)第十一章 三角形 章小结与复习(含解析)
文档属性
| 名称 | 八年级数学上分层优化堂堂清(11)第十一章 三角形 章小结与复习(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
八年级数学上分层优化堂堂清
十一章 三角形
本章小结与复习
老师对你说:
知识点1. 三角形的三边关系
三角形的两边之和大于第三边;
(2)三角形的两边之差小于第三边.
知识点2. 三角形的三条重要线段(高线、中线和角平分线)
(1)三角形的高
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高.
(2)三角形的中线
三角形的一个顶点与它的对边中点的连线叫三角形的中线,
(3)三角形的角平分线
三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.
知识点3. 三角形的内角和定理
三角形的内角和定理:三角形的内角和等于180°.
知识点4. 三角形内角和定理的推论
三角形的外角等于与它不相邻的两个内角之和.
知识点5. 多边形及其内角和
n边形的内角和为(n-2)·180°(n≥3,n是正整数) .
知识点6.多边形外角和:
n边形的外角和恒等于360°,它与边数的多少无关.
考点一 三角形的边
1 ..以下列长度的各组线段为边,能组成三角形的是( )
A.3cm,3cm,6cm B.3cm,4cm,8cm
C.5cm,6cm,9cm D.7cm,6cm,13cm
2 .已知△ABC的三条边分别为a,b,c,化简|a+b﹣c|﹣|b﹣a﹣c|+|a﹣b+c|( )
A.3a﹣b+c B.a+b﹣c C.a﹣b﹣c D.﹣a+3b﹣3c
3.一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长.
【
考点2. 三角形的三条重要线段
4 .△ABC中BC边上的高作法正确的是( )
A.B.
C. D.
5 .如图,ΔABC的面积为8cm,AP垂直ABC的平分线BP于P,则ΔPBC的面积为( )
A.2cm B.3cm C.4cm D.5cm
如图,在中,、分别是的高和角平分线,.
(1)若,求的度数;
(2)试用、的代数式表示的度数_________.
在△ABC中,AB=AC,DB为△ABC的中线,且BD将△ABC周长分为12cm与15cm两部分,求三角形各边长.
考点三 三角形的角
如图,在中,是边上的高,是边上的高,、交于点,平分
(1)若,
①求的度数.
②若平分,试判断与的位置关系,并说明理由.
(2)设,则______(用含的代数式直接表示).
9 .如图,在△ABC中,将CA沿DE翻折,点A落在F处,∠CEF、∠BDF、∠A三者之间的关系是( )
A.∠CEF=∠BDF+∠A B.∠CEF﹣3∠A=∠BDF
C.∠CEF=2(∠BDF+∠A) D.∠CEF﹣∠BDF=2∠A
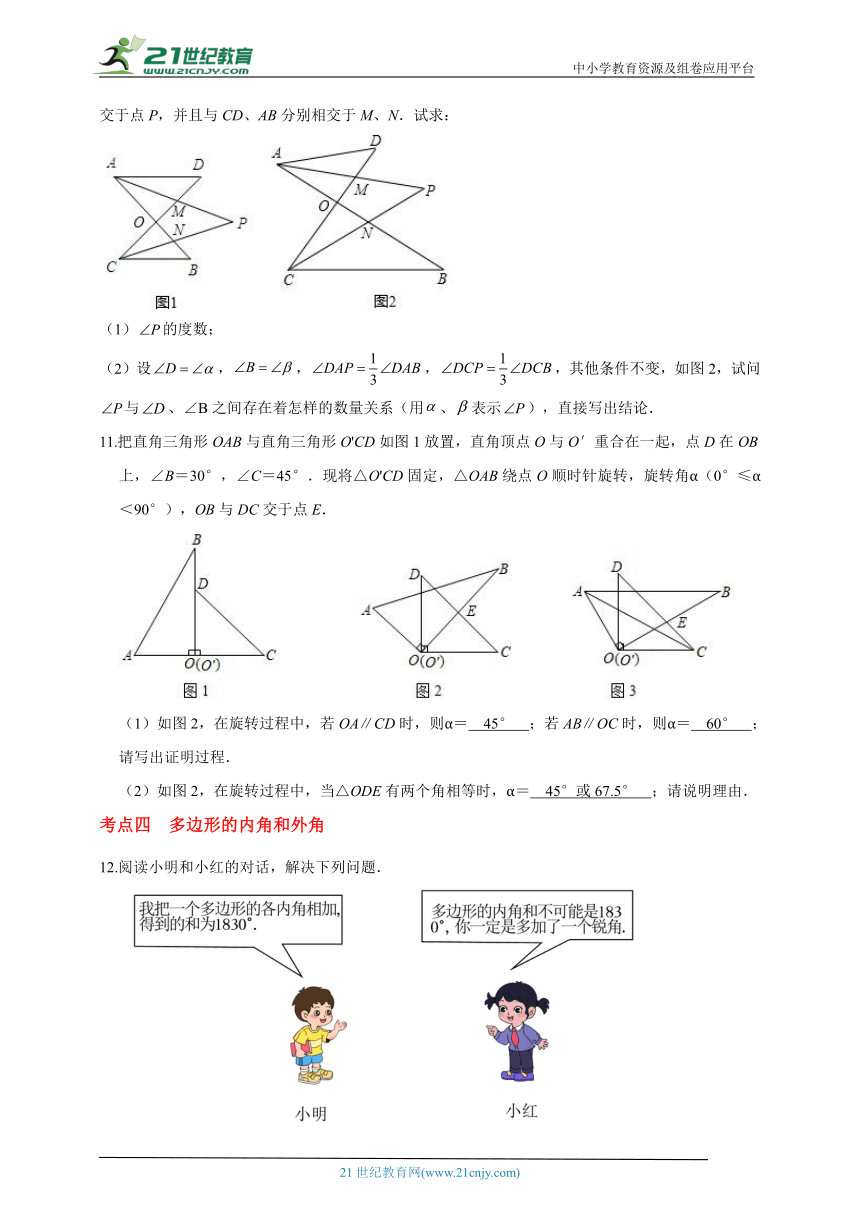
10 .如图1,AB与CD相交于点O,若,,和的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求:
(1)的度数;
(2)设,,,,其他条件不变,如图2,试问与、∠B之间存在着怎样的数量关系(用、表示),直接写出结论.
11.把直角三角形OAB与直角三角形O'CD如图1放置,直角顶点O与O′重合在一起,点D在OB上,∠B=30°,∠C=45°.现将△O'CD固定,△OAB绕点O顺时针旋转,旋转角α(0°≤α<90°),OB与DC交于点E.
(1)如图2,在旋转过程中,若OA∥CD时,则α= 45° ;若AB∥OC时,则α= 60° ;请写出证明过程.
(2)如图2,在旋转过程中,当△ODE有两个角相等时,α= 45°或67.5° ;请说明理由.
考点四 多边形的内角和外角
12.阅读小明和小红的对话,解决下列问题.
(1)这个“多加的锐角”是 30 度.
(2)小明求的是几边形内角和?
(3)若这是个正多边形,则这个正多边形的一个内角是多少度?
13.已知,如图,AD与BC交于点O.
(1)如图1,判断∠A+∠B与∠C+∠D的数量关系: ,并证明你的结论.
(2)如图2,∠A+∠B+∠C+∠D+∠E+∠F+∠M的度数为 .
(3)如图3,若CF平分∠BCD,DE平分∠ADC,CF与DE交于点M,∠E+∠F=50°,请直接写出∠A+∠B= .
如图,淇淇从点A出发,前进10米后向右转20°,再前进10米后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.
(1)求淇淇一共走了多少米?
(2)求这个多边形的内角和.
针对练习
1.△ABC的周长为22cm,AB边比AC边长2cm,BC边是AC边的一半,求△ABC三边的长.
如图,AD是△ABC的高,CE是△ACB的角平分线,F是AC中点,∠ACB=50°,∠BAD=65°.
(1)求∠AEC的度数;
(2)若△BCF与△BAF的周长差为3,AB=7,则BC= 10 .
3.如图已知:AD是△ABC的中线,AB=7cm,AD=5cm,△ABD的周长是18cm,
求BC的长.
4.在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°.求∠BCD和∠ECD的度数.
5.如图,在△ABC中,∠B=25°,∠BAC=31°,过点A作BC边上的高,交BC的延长线于点D,CE平分∠ACD,交AD于点E.
求:(1)∠ACD的度数;
(2)∠AEC的度数.
6 .如图,点A、B、C、D是平面内四个点.连接AB、AC、BD、CD.
(1)如图1,求证:∠BDC=∠A+∠B+∠C;
(2)如图2,若BF平分∠ABD,CE平分∠ACD,BF与CE交于G,∠BDC=m°,∠BGC=n°,求∠A的度数.(用m,n表示)
AD、BE为△ABC的高,AD、BE相交于H点,∠C=50°,求∠BHD.
三角形具有稳定性,所以要使如图所示的五边形木架不变形,至少要钉上( )根木条.
A.1 B.2 C.3 D.4
如图,已知四边形纸片ABCD的边AB∥CD,E是边CD上任意一点,沿BE折叠△BCE,点C落在点F的位置.
(1)如图①,点F落在四边形ABED的内部,探索∠FED,∠ABF,∠C之间的数量关系,并说明理由;
(2)如图②,点F落在边CD的上方,设BF与CD交于点N,直接写出∠FED,∠ABF,∠C之间的数量关系,不需要说明理由.
10 .利用图形这一直观性语言,在一定程度上可以降低我们认识和理解抽象逻辑推理的难度;利用图形建构几何直观,可以轻松实现空间形式和数量关系的相互转化.让我们在如下的问题解决中体验一下吧!
【模块探究】
如图1,求证:∠BOC=∠A+∠B+∠C
【直观应用】
(1)应用上述结论,若图2中,∠EOF=α,则∠A、∠B、∠C、∠D、∠E、∠F的度数之和等于 2α (直接给出结论,不必说明理由)
(2)应用上述结论,求图3所示的五角星中,∠A、∠B、∠C、∠D、∠E的度数之和是多少?证明你的结论;
【类比联系】
如图4,求∠A、∠B、∠C、∠D、∠E、∠F、∠G的度数之和是多少?证明你的结论.
11 .如图,AB⊥CD,垂足为O,点P、Q分别在射线OC、OA上运动(点P、Q都不与点O重合),QE是∠AQP的平分线.
(1)如图1,在点P、Q的运动过程中,若直线QE交∠DPQ的平分线于点H.
①当∠PQB=60°时,∠PHE= 45 °;
②随着点P、Q分别在OC、OA的运动,∠PHE的大小是否是定值?如果是定值,请求出∠PHE的度数;如果不是定值,请说明理由;
(2)如图2,若QE所在直线交∠QPC的平分线于点E时,将△EFG沿FG折叠,使点E落在四边形PFGQ内点E′的位置,猜测∠PFE′与∠QGE′之间的数量关系,并说明理由.
八年级数学上分层优化堂堂清
十一章 三角形
本章小结与复习(解析版)
老师对你说:
知识点1. 三角形的三边关系
三角形的两边之和大于第三边;
(2)三角形的两边之差小于第三边.
知识点2. 三角形的三条重要线段(高线、中线和角平分线)
(1)三角形的高
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高.
(2)三角形的中线
三角形的一个顶点与它的对边中点的连线叫三角形的中线,
(3)三角形的角平分线
三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.
知识点3. 三角形的内角和定理
三角形的内角和定理:三角形的内角和等于180°.
知识点4. 三角形内角和定理的推论
三角形的外角等于与它不相邻的两个内角之和.
知识点5. 多边形及其内角和
n边形的内角和为(n-2)·180°(n≥3,n是正整数) .
知识点6.多边形外角和:
n边形的外角和恒等于360°,它与边数的多少无关.
考点一 三角形的边
1 ..以下列长度的各组线段为边,能组成三角形的是( )
A.3cm,3cm,6cm B.3cm,4cm,8cm
C.5cm,6cm,9cm D.7cm,6cm,13cm
【答案】C
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”进行分析.
【详解】根据三角形的三边关系,
A、,不能构成三角形,不符合题意;
B、,不能构成三角形,不符合题意;
C、,能构成三角形,符合题意;
D、,不能构成三角形,不符合题意;
故选:C.
【点评】此题考查了三角形的三边关系,判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数.
2 .已知△ABC的三条边分别为a,b,c,化简|a+b﹣c|﹣|b﹣a﹣c|+|a﹣b+c|( )
A.3a﹣b+c B.a+b﹣c C.a﹣b﹣c D.﹣a+3b﹣3c
【答案】B
【分析】根据三角形的任意两边之和大于第三边可得a+b c>0,a b+c>0,b a c<0,再根据绝对值的性质去掉绝对值符号,然后利用整式的加减运算进行计算即可得解.
【详解】解:∵a、b、c分别为△ABC的三边长,
∴a+b c>0,b a c<0,a b+c>0,
∴|a+b c| |b a c|+|a b+c|
=a+b c (a+c b)+a b+c
=a+b c a c+b+a b+c
=a+b c.
故选:B.
【点评】本题考查了三角形的三边关系,绝对值的性质,整式的加减运算,熟记性质并去掉绝对值符号是解题的关键.
3.一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长.
【分析】题目给出等腰三角形有一条边长为6cm,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
【解答】解:(1)当6是腰时,底边=20﹣6×2=8cm,即其它两边是6cm,8cm,此时6+6=12,能构成三角形;
(2)当6是底边时,腰=(20﹣6)÷2=7cm,此时能构成三角形,所以其它两边是7cm、7cm.
因此其它两边长分别为7cm,7cm,
综上所述两边长分别为6cm,8cm或7cm,7cm.
【点评】本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.
考点2. 三角形的三条重要线段
4 .△ABC中BC边上的高作法正确的是( )
A.B.
C. D.
【分析】根据三角形高线的定义:过三角形的顶点向对边引垂线,顶点和垂足之间的线段叫做三角形的高线解答.
【解答】解:为△ABC中BC边上的高的是D选项.
故选:D.
【点评】本题考查了三角形的角平分线、中线、高线,熟记高线的定义是解题的关键.
5 .如图,ΔABC的面积为8cm,AP垂直ABC的平分线BP于P,则ΔPBC的面积为( )
A.2cm B.3cm C.4cm D.5cm
【答案】C
【解析】解:延长AP交BC于E,
∵AP垂直ABC的平分线BP于P,
∠ABP=∠EBP,∠APB=∠BPE=90°,
又∵BP=BP, ∴△ABP≌△BEP,
∴S△ABP=S△BEP,AP=PE,
∴△APC和△CPE等底同高,∴S△APC=S△PCE,
∴S△PBC=S△PBE+S△PCE=S△ABC=4cm2,故选:C.
如图,在中,、分别是的高和角平分线,.
(1)若,求的度数;
(2)试用、的代数式表示的度数_________.
【答案】(1);(2)
【解析】(1)解:,
,
是的平分线,.
是高线,,,
.
(2)解:,;,
是的平分线,.
是高线,,,
.
在△ABC中,AB=AC,DB为△ABC的中线,且BD将△ABC周长分为12cm与15cm两部分,求三角形各边长.
【分析】根据中线的定义得到AD=CD,设AD=CD=x,则AB=2x,分类讨论:当x+2x=12,BC+x=15;当x+2x=15,BC+x=12,然后分别求出x和BC,即可得到三角形三边的长.
【解答】解:如图,∵DB为△ABC的中线
∴AD=CD,
设AD=CD=x,则AB=2x,
当x+2x=12,解得x=4,
BC+x=15,解得BC=11,
此时△ABC的三边长为:AB=AC=8,BC=11;
当x+2x=15,BC+x=12,解得x=5,BC=7,
此时△ABC的三边长为:AB=AC=10,BC=7.
【点评】本题考查了三角形的角平分线、中线和高:三角形的一个顶点向底边作垂线,垂足与顶点之间的线段叫做三角形的高;三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线;三角形一边的中点与此边所对顶点的连线叫做三角形的中线.
考点三 三角形的角
如图,在中,是边上的高,是边上的高,、交于点,平分
(1)若,
①求的度数.
②若平分,试判断与的位置关系,并说明理由.
(2)设,则______(用含的代数式直接表示).
【答案】(1)①∠CFG;②FG∥AH;(2)180°-α
【解析】(1)解:①∵BD是AC边上的高,CE是AB边上的高,
∴∠CEA=∠ADB=90°,
∵∠BAC=56°,∠ACB=70°,∴∠ABC=180°-∠ACB-∠BAC=54°,
∴∠ABD=90°-∠BAC=34°,∠ACE=90°-∠BAC=34°,
∴∠FBG=∠ABC-∠ABD=20°,∠FCG=∠ACB-∠ACE=36°,
∴∠BFC=180°-∠DBC-∠FCG=124°,
∵FG平分∠BFC,∴∠CFG=;
②∵AH平分∠BAC,∴∠BAH=,
∴∠BHA=180°-∠HAB-∠ABH=98°,
在 BGF中,∠FGB=180°-∠FBG-∠BFG=98°,
∴FG∥AH;
(2)∵BD是AC边上的高,CE是AB边上的高,
∴∠CEA=∠ADB=90°,
∵∠BAC=α,∠ABC+∠ACB=180°-α,
∴∠ABD=90°-∠BAC=90°-α,∠ACE=90°-∠BAC=90°-α,
∴∠FBG+∠FCG=∠ABC+∠ACB-∠ABD-∠ACE=180°-α-(90°-α)-( 90°-α)= α,
∴∠BFC=180°-∠FBG-∠FCG =180°-α,
故答案为:180°-α.
9 .如图,在△ABC中,将CA沿DE翻折,点A落在F处,∠CEF、∠BDF、∠A三者之间的关系是( )
A.∠CEF=∠BDF+∠A B.∠CEF﹣3∠A=∠BDF
C.∠CEF=2(∠BDF+∠A) D.∠CEF﹣∠BDF=2∠A
【分析】根据三角形内角和定理可得∠CEF=∠A+∠AOE,∠AOE=∠F+∠BDF,从而可得∠CEF=∠A+∠F+∠BDF,由折叠性质可得∠A=∠F,从而可得∠CEF=2∠A+∠BDF,即可求解.
【解答】解:如图,
∵∠CEF=∠A+∠AOE,∠AOE=∠F+∠BDF,
∴∠CEF=∠A+∠F+∠BDF,
由折叠性质可得:
∠A=∠F,
∴∠CEF=2∠A+∠BDF,
∴∠CEF﹣∠BDF=2∠A,
故选:D.
【点评】本题考查三角形内角和定理,折叠的性质,解题的关键是正确利用△AOE和△DOF的内角和关系.
10 .如图1,AB与CD相交于点O,若,,和的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求:
(1)的度数;
(2)设,,,,其他条件不变,如图2,试问与、∠B之间存在着怎样的数量关系(用、表示),直接写出结论.
【答案】(1)33°;(2) .
【解析】解:(1)∵AP是∠DAB的角平分线,CP是∠DCB的角平分线
∴∠DAP=PAB,∠DCP=∠PCB
∵∠P+∠PAB=∠B+∠PCB,∠P+∠PCD=∠D+∠DAP
∴∠P+∠PAB+∠P+∠PCD=∠B+∠PCB+∠D+∠DAP
∴2∠P=∠B+∠D
∵∠B=28°,∠D=38°
∴∠P=33°
(2) ∠P=
∵∠P+∠PCD=∠D+∠DAP
∴∠PCD-∠DAP=∠D-∠P
∵∠D+∠DAO=∠B+∠OCB
∴∠DAB-∠DCB=∠B-∠D
∵,
∴∠DAB-∠DCB=3(∠DAP-∠DCP)
∴∠B-∠D=3(∠P-∠D)
∵,
∴∠P=
11.把直角三角形OAB与直角三角形O'CD如图1放置,直角顶点O与O′重合在一起,点D在OB上,∠B=30°,∠C=45°.现将△O'CD固定,△OAB绕点O顺时针旋转,旋转角α(0°≤α<90°),OB与DC交于点E.
(1)如图2,在旋转过程中,若OA∥CD时,则α= 45° ;若AB∥OC时,则α= 60° ;请写出证明过程.
(2)如图2,在旋转过程中,当△ODE有两个角相等时,α= 45°或67.5° ;请说明理由.
【分析】(1)利用平行线的性质求解即可;
(2)分两种情形:当∠D=∠DOE=45°时,当∠DOE=∠DEO=67.5°时,分别求解.
【解答】解:(1)当OA∥CD时,
∠AOD=∠D=45°,
∴α=45°,
当AB∥OC时,
∠AOD+∠A=90°,
∴∠AOD=30°,
∴α=60°,
故答案为:45°,60°.
(2)当∠D=∠DOE=45°时,α=45°,
当∠DOE=∠DEO=67.5°时,α=67.5°,
故答案为:45°或67.5°.
【点评】本题考查直角三角形的性质,三角形内角和定理等知识,解题的关键是学会由分类讨论的思想思考问题,属于中考常考题型.
考点四 多边形的内角和外角
12.阅读小明和小红的对话,解决下列问题.
(1)这个“多加的锐角”是 30 度.
(2)小明求的是几边形内角和?
(3)若这是个正多边形,则这个正多边形的一个内角是多少度?
【分析】(1)根据多边形内角和的计算方法进行估算即可;
(2)根据对话和多边形内角和的计算方法列方程求解即可;
(3)根据正多边形内角的计算方法进行计算即可.
【解答】解:(1)12边形的内角和为(12﹣2)×180°=1800°,而13边形的内角和为(13﹣2)×180°=1980°,
由于小红说“多边形的内角和不可能是1830°,你一定是多加了一个锐角”,
所以这个“多加的锐角”是1830°﹣1800°=30°,
故答案为:30;
(2)设这个多边形为n边形,由题意得,
(n﹣2)×180°=1800°,
解得n=12,
答:小明求的是12边形内角和;
(3)正十二边形的每一个内角为=150°,
答:这个正多边形的一个内角是150°.
【点评】本题考查多边形的内角和和外角和,掌握多边形内角和的计算方法以及正多边形的性质是正确解答的前提.
13.已知,如图,AD与BC交于点O.
(1)如图1,判断∠A+∠B与∠C+∠D的数量关系: ,并证明你的结论.
(2)如图2,∠A+∠B+∠C+∠D+∠E+∠F+∠M的度数为 .
(3)如图3,若CF平分∠BCD,DE平分∠ADC,CF与DE交于点M,∠E+∠F=50°,请直接写出∠A+∠B= .
【分析】(1)根据三角形内角和定理以及对顶角相等可得结论;
(2)利用(1)的结论以及五边形的内角和计算方法进行计算即可;
(3)利用角平分线的定义以及(1)的结论可得∠A+∠B=∠OCD+∠ODC=2(∠E+∠F)即可.
【解答】解:(1)∵∠AOB+∠A+∠B=180°=∠COD+∠C+∠D,∠AOB=∠COD,
∴∠A+∠B=∠C+∠D,
故答案为:∠A+∠B=∠C+∠D;
(2)如图2,连接AB,
由(1)得,∠OBA+∠OAB=∠C+∠D,
∴∠DAM+∠CBE+∠C+∠D+∠E+∠F+∠M的度数为五边形ABEFM的内角和,
即(5﹣2)×180°=540°,
故答案为:540°;
(3)∵CF平分∠BCD,DE平分∠ADC,
∴∠MCD=∠OCD,∠MDC=∠ODC,
由(1)可得,∠E+∠F=∠MCD+∠MDC,
∴∠OCD+∠ODC=50°,
∴∠OCD+∠ODC=100°,
∴∠A+∠B=∠OCD+∠ODC=100°,
故答案为:100°.
【点评】本题考查多边形的内角与外角,三角形内角和定理以及角平分线的定义,掌握三角形内角和是180°,角平分线的定义以及多边形内角和的计算方法是正确解答的前提.
如图,淇淇从点A出发,前进10米后向右转20°,再前进10米后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.
(1)求淇淇一共走了多少米?
(2)求这个多边形的内角和.
【分析】(1)第一次回到出发点A时,所经过的路线正好构成一个外角是20度的正多边形,求得边数,即可求解;
(2)根据多边形的内角和公式即可得到结论.
【解答】解:(1)∵所经过的路线正好构成一个外角是20度的正多边形,
∴360÷20=18,
18×10=180(米).
答:淇淇一共走了180米.
(2)根据题意,得(18﹣2)×180°=2880°,
答:这个多边形的内角和是2880°.
【点评】本题考查了正多边形的外角的计算以及多边形的内角和,第一次回到出发点A时,所经过的路线正好构成一个外角是20度的正多边形是关键.
针对练习
1.△ABC的周长为22cm,AB边比AC边长2cm,BC边是AC边的一半,求△ABC三边的长.
【分析】首先利用一个未知数表示出各边长,进而得出等式求出各边长即可.
【解答】解:设BC=x,则AC=2x,AB=2x+2,
∵AB+BC+AC=22,
∴2x+2x+2+x=22,
解得;x=4,
∴AC=8cm,BC=4cm,AB=10cm.
【点评】此题主要考查了三角形周长公式,根据题意得出关于三角形周长的方程是解题关键.
如图,AD是△ABC的高,CE是△ACB的角平分线,F是AC中点,∠ACB=50°,∠BAD=65°.
(1)求∠AEC的度数;
(2)若△BCF与△BAF的周长差为3,AB=7,则BC= 10 .
【分析】(1)根据三角形的高的概念得到∠ADB=90°,根据直角三角形的性质求出∠ABD,根据角平分线的定义求出∠ECB,根据三角形的外角性质计算即可;
(2)根据三角形的中线的概念得到AF=FC,根据三角形的周长公式计算,得到答案.
【解答】解:(1)∵AD是△ABC的高,
∴∠ADB=90°,
∵∠BAD=65°,
∴∠ABD=90°﹣65°=25°,
∵CE是△ACB的角平分线,∠ACB=50°,
∴∠ECB=∠ACB=25°,
∴∠AEC=∠ABD+∠ECB=25°+25°=50°;
(2)∵F是AC中点,
∴AF=FC,
∵△BCF与△BAF的周长差为3,
∴(BC+CF+BF)﹣(AB+AF+BF)=3,
∴BC﹣AB=3,
∵AB=7,
∴BC=10,
故答案为:10.
【点评】本题考查的是三角形的三角形的角平分线、中线和高,从三角形的一个顶点向对边作垂线,垂足与顶点之间的线段叫做三角形的高;三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线;三角形一边的中点与此边所对顶点的连线叫做三角形的中线.
3.如图已知:AD是△ABC的中线,AB=7cm,AD=5cm,△ABD的周长是18cm,
求BC的长.
【分析】根据三角形中线的定义得到BC=2BD,根据三角形周长公式即可得到结论.
【解答】解:∵AD是△ABC的中线,
∴BC=2BD,
∵AB=7cm,AD=5cm,△ABD的周长是18cm,
∴BD=18﹣7﹣5=6(cm),
∴BC的长为12cm.
【点评】本题考查了三角形的角平分线、中线和高,熟练掌握三角形中线的定义是解题的关键.
4.在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°.求∠BCD和∠ECD的度数.
【分析】由CD⊥AB与∠B=60°,根据两锐角互余,即可求得∠BCD的度数,又由∠A=20°,∠B=60°,求得∠ACB的度数,由CE是∠ACB的平分线,可求得∠ACE的度数,然后根据三角形外角的性质,求得∠CEB的度数.
【解答】解:∵CD⊥AB,
∴∠CDB=90°,
∵∠B=60°,
∴∠BCD=90°﹣∠B=90°﹣60°=30°;
∵∠A=20°,∠B=60°,∠A+∠B+∠ACB=180°,
∴∠ACB=100°,
∵CE是∠ACB的平分线,
∴∠ACE=∠ACB=50°,
∴∠CEB=∠A+∠ACE=20°+50°=70°,
∠ECD=90°﹣70°=20°.
或∠ECD=∠ECB﹣∠BCD=50°﹣30°=20°.
【点评】此题考查了三角形的内角和定理,三角形外角的性质以及三角形高线,角平分线的定义等知识.此题难度不大,解题的关键是数形结合思想的应用.
5.如图,在△ABC中,∠B=25°,∠BAC=31°,过点A作BC边上的高,交BC的延长线于点D,CE平分∠ACD,交AD于点E.
求:(1)∠ACD的度数;
(2)∠AEC的度数.
【分析】(1)利用三角形的外角的性质求解即可.
(2)求出∠ECD,∠D,利用三角形的外角的性质求解即可.
【解答】解:(1)∵∠ACD=∠B+∠BAC,∠B=25°,∠BAC=31°,
∴∠ACD=25°+31°=56°.
(2)∵AD⊥BD,
∴∠D=90°,
∵∠ACD=56°,CE平分∠ACD,
∴∠ECD=∠ACD=28°,
∴∠AEC=∠ECD+∠D=28°+90°=118°.
【点评】本题考查三角形内角和定理,三角形的外角的性质,角平分线的定义等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
6 .如图,点A、B、C、D是平面内四个点.连接AB、AC、BD、CD.
(1)如图1,求证:∠BDC=∠A+∠B+∠C;
(2)如图2,若BF平分∠ABD,CE平分∠ACD,BF与CE交于G,∠BDC=m°,∠BGC=n°,求∠A的度数.(用m,n表示)
【分析】(1)由三角形的外角性质,即可证明;
(2)由(1)的结论,即可求解.
【解答】(1)证明:延长BD交AC于E,
∵∠DEC=∠A+∠B,
∠BDC=∠DEC+∠C,
∴∠BDC=∠A+∠B+∠C,
(2)解:∵BF平分∠ABD,CE平分∠ACD,
∴∠DBG=∠ABF,∠DCG=∠ACE,
∵∠BDC=∠BGC+∠DBG+∠DCG,
∴∠DBG+∠DCG=∠BDC﹣∠BGC=m°﹣n°,
∴∠ABF+∠ACE=∠DBG+∠DCG=m°﹣n°,
∵∠BGC=∠A+∠ABF+∠ACE,
∴∠A=∠BGC﹣(∠ABF+∠ACE),
∴∠A=n°﹣(m°﹣n°)=2n°﹣m°.
【点评】本题考查三角形外角的性质,关键是掌握三角形外角的性质:三角形的一个外角等于和它不相邻的两个内角的和.
AD、BE为△ABC的高,AD、BE相交于H点,∠C=50°,求∠BHD.
【分析】根据同角的余角相等求出∠BHD=∠C,从而得解.
【解答】解:∵AD是△ABC的高,
∴∠BHD+∠HBD=90°,
∵BE是△ABC的高,
∴∠HBD+∠C=90°,
∴∠BHD=∠C,
∵∠C=50°,
∴∠BHD=50°.
【点评】本题考查了直角三角形两锐角互余的性质,同角的余角相等的性质,熟记性质并准确识图是解题的关键.
三角形具有稳定性,所以要使如图所示的五边形木架不变形,至少要钉上( )根木条.
A.1 B.2 C.3 D.4
【分析】三角形具有稳定性,所以要使五边形木架不变形需把它分成三角形,即过六边形的一个顶点作对角线,有几条对角线,就至少要钉上几根木条.
【解答】解:过五边形的一个顶点作对角线,有5﹣3=2条对角线,所以至少要钉上2根木条.
故选:B.
【点评】本题考查了三角形具有稳定性,是基础题,作出图形更形象直观
如图,已知四边形纸片ABCD的边AB∥CD,E是边CD上任意一点,沿BE折叠△BCE,点C落在点F的位置.
(1)如图①,点F落在四边形ABED的内部,探索∠FED,∠ABF,∠C之间的数量关系,并说明理由;
(2)如图②,点F落在边CD的上方,设BF与CD交于点N,直接写出∠FED,∠ABF,∠C之间的数量关系,不需要说明理由.
【分析】(1)数量关系:∠FED+∠ABF=∠C.理由:过点F作MN∥CD,交AD于点M,交BC于点N,由平行线的性质可得∠FED=∠EFN,根据平行公理的推论可得MN∥AB,继而得到∠NFB=∠ABF,再结合折叠的性质可得数量关系.
(2)过点F作GH∥CD,由平行线的性质可得∠FED=∠HFE,根据平行公理的推论可得GH∥AB,继而得到得∠ABF=∠HFB,再结合折叠的性质可得数量关系.
【解答】解:(1)∠FED,∠ABF,∠C 之间的数量关系:∠FED+∠ABF=∠C.
理由如下:如图①,过点F作MN∥CD,交AD于点M,交BC于点N
则∠FED=∠EFN,
∵AB∥CD,
∴MN∥AB,
∴∠NFB=∠ABF,
∴∠FED+∠ABF=∠EFN+∠NFB=∠EFB,
由折叠的性质得,△BCE≌△BFE,
∴∠EFB=∠C,
∴∠FED+∠ABF=∠C,
∴∠FED,∠ABF,∠C 之间的数量关系是:∠FED+∠ABF=∠C.
(2)如图②,过点F作GH∥CD
则∠FED=∠HFE,
∵AB∥CD,
∴GH∥AB,
∴∠ABF=∠HFB=∠HFE+∠BFE=∠FED+∠BFE,
由折叠的性质得,△BCE≌△BFE,
∴∠BFE=∠C,
∴∠ABF=∠FED+∠C,即∠ABF﹣∠FED=∠C,
∴∠FED,∠ABF,∠C 之间的数量关系是:∠ABF﹣∠FED=∠C.
【点评】本题考查折叠的性质,平行线的性质,平行公理的推论.掌握折叠的性质和平行线的性质是解题的关键.
10 .利用图形这一直观性语言,在一定程度上可以降低我们认识和理解抽象逻辑推理的难度;利用图形建构几何直观,可以轻松实现空间形式和数量关系的相互转化.让我们在如下的问题解决中体验一下吧!
【模块探究】
如图1,求证:∠BOC=∠A+∠B+∠C
【直观应用】
(1)应用上述结论,若图2中,∠EOF=α,则∠A、∠B、∠C、∠D、∠E、∠F的度数之和等于 2α (直接给出结论,不必说明理由)
(2)应用上述结论,求图3所示的五角星中,∠A、∠B、∠C、∠D、∠E的度数之和是多少?证明你的结论;
【类比联系】
如图4,求∠A、∠B、∠C、∠D、∠E、∠F、∠G的度数之和是多少?证明你的结论.
【分析】模块探究,由三角形外角的性质,即可证明;
直观应用,应用模块探究的结论,即可解决问题;
类比联系,应用模块探究的结论,即可解决问题.
【解答】
模块探究,证明:延长BO交AC于D,
∵∠BOC=∠C+∠CDO,∠CDO=∠A+∠B,
∴∠BOC=∠A+∠B+∠C;
直观应用,解:(1)由上述结论得:∠BOC=∠A+∠B+∠C,∠EOF=∠D+∠E+∠F,
∴∠A+∠B+∠C+∠D+∠E+∠F=∠BOC+∠EOF=2α,
故答案为:2α.
(2)∠A、∠B、∠C、∠D、∠E的度数之和是180°,
证明:∵∠BOC=∠A+∠B+∠C,∠COD=∠E+∠D,
∴∠A+∠B+∠C+∠E+∠D=∠BOC+∠COD=180°;
类比联系:∵∠DMN=∠G+∠GNM,∠GNM=∠BNC=∠F+∠B+∠C,
∴∠DMN=∠G+∠F+∠B+∠C,
∵∠EMD=∠A+∠E+∠D
∴∠A+∠E+∠D+=∠G+∠F+∠B+∠C=∠EMD+∠DMN=180°.
【点评】本题考查角的计算,关键是注意应用题目中的结论.
11 .如图,AB⊥CD,垂足为O,点P、Q分别在射线OC、OA上运动(点P、Q都不与点O重合),QE是∠AQP的平分线.
(1)如图1,在点P、Q的运动过程中,若直线QE交∠DPQ的平分线于点H.
①当∠PQB=60°时,∠PHE= 45 °;
②随着点P、Q分别在OC、OA的运动,∠PHE的大小是否是定值?如果是定值,请求出∠PHE的度数;如果不是定值,请说明理由;
(2)如图2,若QE所在直线交∠QPC的平分线于点E时,将△EFG沿FG折叠,使点E落在四边形PFGQ内点E′的位置,猜测∠PFE′与∠QGE′之间的数量关系,并说明理由.
【分析】(1)①先根据垂直的定义求出∠POQ=90°,即可利用三角形内角和定理和邻补角的定义求出∠QPO=30°,∠AQP=120°,再由角平分线的定义分别求出∠EQP=60°,∠HPQ=15°,最后根据三角形外角的性质求解即可;②同①方法求解即可;
(2)如图所示,连接EE',先求出∠CPQ+∠PQA=270°,再由角平分线的定义求出∠EPQ+∠EQP=135°,则∠PEQ=45°,由折叠的性质可知∠GE'F=∠PEQ=45°,进而推出∠EFE'+∠EFE'=270°即可得到答案.
【解答】解:(1)①∵AB⊥CD,
∴∠POQ=90°,
∴∠PQO+∠QPO=90°,
∵∠PQB=60°,
∴∠QPO=30°,∠AQP=120°,
∵EQ平分∠AQP,PH平分∠QPO,
∴,,
∴∠H=∠EQP﹣∠HPQ=45°,
故答案为:45;
②∠PHE 是一个定值,∠PHE=45°,理由如下:
∵AB⊥CD,
∴∠POQ=90°,
∴∠PQO+∠QPO=90°,
∴∠QPO=90°﹣∠PQO,∠AQP=180°﹣∠PQO,
∵EQ平分∠AQP,PH平分∠QPO,
∴,,
∴∠H=∠EQP﹣∠HPQ=45°;
(2)∠PFE'+∠QGE'=90°,理由如下:
如图2所示,连接EE',
∵AB⊥CD,
∴∠POQ=90°,
∴∠PQO+∠QPO=90°,
∵∠CPQ+∠QPO=180°,∠PQA+∠PQO=180°,
∴180°﹣∠CPQ+180°﹣∠PQA=90°,
∴∠CPQ+∠PQA=270°,
∵QE,PE分别平分∠PQA,∠CPQ,
∴,
∴,
∴∠PEQ=180°﹣∠EPQ﹣∠EQP=45°,
由折叠的性质可知∠GE'F=∠PEQ=45°,
∵∠FEE'+∠EFE'+∠EE'F=180°=∠GEE'+∠EGE'+∠EE'G,
∴∠FEG+∠FE'G+∠EFE'+∠EGE'=360°,
∴∠EFE'+∠EFE'=270°,
∵∠EFE'+∠PFE'=180°=∠EGE'+∠QGE',
∴∠PFE'+∠QGE'=360°﹣∠EFE'﹣∠EFE'=90°.
【点评】本题主要考查了三角形内角和定理,三角形外角的性质,角平分线的定义,邻补角,熟知三角形内角和定理和角平分线的定义是解题的关键
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
八年级数学上分层优化堂堂清
十一章 三角形
本章小结与复习
老师对你说:
知识点1. 三角形的三边关系
三角形的两边之和大于第三边;
(2)三角形的两边之差小于第三边.
知识点2. 三角形的三条重要线段(高线、中线和角平分线)
(1)三角形的高
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高.
(2)三角形的中线
三角形的一个顶点与它的对边中点的连线叫三角形的中线,
(3)三角形的角平分线
三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.
知识点3. 三角形的内角和定理
三角形的内角和定理:三角形的内角和等于180°.
知识点4. 三角形内角和定理的推论
三角形的外角等于与它不相邻的两个内角之和.
知识点5. 多边形及其内角和
n边形的内角和为(n-2)·180°(n≥3,n是正整数) .
知识点6.多边形外角和:
n边形的外角和恒等于360°,它与边数的多少无关.
考点一 三角形的边
1 ..以下列长度的各组线段为边,能组成三角形的是( )
A.3cm,3cm,6cm B.3cm,4cm,8cm
C.5cm,6cm,9cm D.7cm,6cm,13cm
2 .已知△ABC的三条边分别为a,b,c,化简|a+b﹣c|﹣|b﹣a﹣c|+|a﹣b+c|( )
A.3a﹣b+c B.a+b﹣c C.a﹣b﹣c D.﹣a+3b﹣3c
3.一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长.
【
考点2. 三角形的三条重要线段
4 .△ABC中BC边上的高作法正确的是( )
A.B.
C. D.
5 .如图,ΔABC的面积为8cm,AP垂直ABC的平分线BP于P,则ΔPBC的面积为( )
A.2cm B.3cm C.4cm D.5cm
如图,在中,、分别是的高和角平分线,.
(1)若,求的度数;
(2)试用、的代数式表示的度数_________.
在△ABC中,AB=AC,DB为△ABC的中线,且BD将△ABC周长分为12cm与15cm两部分,求三角形各边长.
考点三 三角形的角
如图,在中,是边上的高,是边上的高,、交于点,平分
(1)若,
①求的度数.
②若平分,试判断与的位置关系,并说明理由.
(2)设,则______(用含的代数式直接表示).
9 .如图,在△ABC中,将CA沿DE翻折,点A落在F处,∠CEF、∠BDF、∠A三者之间的关系是( )
A.∠CEF=∠BDF+∠A B.∠CEF﹣3∠A=∠BDF
C.∠CEF=2(∠BDF+∠A) D.∠CEF﹣∠BDF=2∠A
10 .如图1,AB与CD相交于点O,若,,和的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求:
(1)的度数;
(2)设,,,,其他条件不变,如图2,试问与、∠B之间存在着怎样的数量关系(用、表示),直接写出结论.
11.把直角三角形OAB与直角三角形O'CD如图1放置,直角顶点O与O′重合在一起,点D在OB上,∠B=30°,∠C=45°.现将△O'CD固定,△OAB绕点O顺时针旋转,旋转角α(0°≤α<90°),OB与DC交于点E.
(1)如图2,在旋转过程中,若OA∥CD时,则α= 45° ;若AB∥OC时,则α= 60° ;请写出证明过程.
(2)如图2,在旋转过程中,当△ODE有两个角相等时,α= 45°或67.5° ;请说明理由.
考点四 多边形的内角和外角
12.阅读小明和小红的对话,解决下列问题.
(1)这个“多加的锐角”是 30 度.
(2)小明求的是几边形内角和?
(3)若这是个正多边形,则这个正多边形的一个内角是多少度?
13.已知,如图,AD与BC交于点O.
(1)如图1,判断∠A+∠B与∠C+∠D的数量关系: ,并证明你的结论.
(2)如图2,∠A+∠B+∠C+∠D+∠E+∠F+∠M的度数为 .
(3)如图3,若CF平分∠BCD,DE平分∠ADC,CF与DE交于点M,∠E+∠F=50°,请直接写出∠A+∠B= .
如图,淇淇从点A出发,前进10米后向右转20°,再前进10米后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.
(1)求淇淇一共走了多少米?
(2)求这个多边形的内角和.
针对练习
1.△ABC的周长为22cm,AB边比AC边长2cm,BC边是AC边的一半,求△ABC三边的长.
如图,AD是△ABC的高,CE是△ACB的角平分线,F是AC中点,∠ACB=50°,∠BAD=65°.
(1)求∠AEC的度数;
(2)若△BCF与△BAF的周长差为3,AB=7,则BC= 10 .
3.如图已知:AD是△ABC的中线,AB=7cm,AD=5cm,△ABD的周长是18cm,
求BC的长.
4.在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°.求∠BCD和∠ECD的度数.
5.如图,在△ABC中,∠B=25°,∠BAC=31°,过点A作BC边上的高,交BC的延长线于点D,CE平分∠ACD,交AD于点E.
求:(1)∠ACD的度数;
(2)∠AEC的度数.
6 .如图,点A、B、C、D是平面内四个点.连接AB、AC、BD、CD.
(1)如图1,求证:∠BDC=∠A+∠B+∠C;
(2)如图2,若BF平分∠ABD,CE平分∠ACD,BF与CE交于G,∠BDC=m°,∠BGC=n°,求∠A的度数.(用m,n表示)
AD、BE为△ABC的高,AD、BE相交于H点,∠C=50°,求∠BHD.
三角形具有稳定性,所以要使如图所示的五边形木架不变形,至少要钉上( )根木条.
A.1 B.2 C.3 D.4
如图,已知四边形纸片ABCD的边AB∥CD,E是边CD上任意一点,沿BE折叠△BCE,点C落在点F的位置.
(1)如图①,点F落在四边形ABED的内部,探索∠FED,∠ABF,∠C之间的数量关系,并说明理由;
(2)如图②,点F落在边CD的上方,设BF与CD交于点N,直接写出∠FED,∠ABF,∠C之间的数量关系,不需要说明理由.
10 .利用图形这一直观性语言,在一定程度上可以降低我们认识和理解抽象逻辑推理的难度;利用图形建构几何直观,可以轻松实现空间形式和数量关系的相互转化.让我们在如下的问题解决中体验一下吧!
【模块探究】
如图1,求证:∠BOC=∠A+∠B+∠C
【直观应用】
(1)应用上述结论,若图2中,∠EOF=α,则∠A、∠B、∠C、∠D、∠E、∠F的度数之和等于 2α (直接给出结论,不必说明理由)
(2)应用上述结论,求图3所示的五角星中,∠A、∠B、∠C、∠D、∠E的度数之和是多少?证明你的结论;
【类比联系】
如图4,求∠A、∠B、∠C、∠D、∠E、∠F、∠G的度数之和是多少?证明你的结论.
11 .如图,AB⊥CD,垂足为O,点P、Q分别在射线OC、OA上运动(点P、Q都不与点O重合),QE是∠AQP的平分线.
(1)如图1,在点P、Q的运动过程中,若直线QE交∠DPQ的平分线于点H.
①当∠PQB=60°时,∠PHE= 45 °;
②随着点P、Q分别在OC、OA的运动,∠PHE的大小是否是定值?如果是定值,请求出∠PHE的度数;如果不是定值,请说明理由;
(2)如图2,若QE所在直线交∠QPC的平分线于点E时,将△EFG沿FG折叠,使点E落在四边形PFGQ内点E′的位置,猜测∠PFE′与∠QGE′之间的数量关系,并说明理由.
八年级数学上分层优化堂堂清
十一章 三角形
本章小结与复习(解析版)
老师对你说:
知识点1. 三角形的三边关系
三角形的两边之和大于第三边;
(2)三角形的两边之差小于第三边.
知识点2. 三角形的三条重要线段(高线、中线和角平分线)
(1)三角形的高
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高.
(2)三角形的中线
三角形的一个顶点与它的对边中点的连线叫三角形的中线,
(3)三角形的角平分线
三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.
知识点3. 三角形的内角和定理
三角形的内角和定理:三角形的内角和等于180°.
知识点4. 三角形内角和定理的推论
三角形的外角等于与它不相邻的两个内角之和.
知识点5. 多边形及其内角和
n边形的内角和为(n-2)·180°(n≥3,n是正整数) .
知识点6.多边形外角和:
n边形的外角和恒等于360°,它与边数的多少无关.
考点一 三角形的边
1 ..以下列长度的各组线段为边,能组成三角形的是( )
A.3cm,3cm,6cm B.3cm,4cm,8cm
C.5cm,6cm,9cm D.7cm,6cm,13cm
【答案】C
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”进行分析.
【详解】根据三角形的三边关系,
A、,不能构成三角形,不符合题意;
B、,不能构成三角形,不符合题意;
C、,能构成三角形,符合题意;
D、,不能构成三角形,不符合题意;
故选:C.
【点评】此题考查了三角形的三边关系,判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数.
2 .已知△ABC的三条边分别为a,b,c,化简|a+b﹣c|﹣|b﹣a﹣c|+|a﹣b+c|( )
A.3a﹣b+c B.a+b﹣c C.a﹣b﹣c D.﹣a+3b﹣3c
【答案】B
【分析】根据三角形的任意两边之和大于第三边可得a+b c>0,a b+c>0,b a c<0,再根据绝对值的性质去掉绝对值符号,然后利用整式的加减运算进行计算即可得解.
【详解】解:∵a、b、c分别为△ABC的三边长,
∴a+b c>0,b a c<0,a b+c>0,
∴|a+b c| |b a c|+|a b+c|
=a+b c (a+c b)+a b+c
=a+b c a c+b+a b+c
=a+b c.
故选:B.
【点评】本题考查了三角形的三边关系,绝对值的性质,整式的加减运算,熟记性质并去掉绝对值符号是解题的关键.
3.一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长.
【分析】题目给出等腰三角形有一条边长为6cm,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
【解答】解:(1)当6是腰时,底边=20﹣6×2=8cm,即其它两边是6cm,8cm,此时6+6=12,能构成三角形;
(2)当6是底边时,腰=(20﹣6)÷2=7cm,此时能构成三角形,所以其它两边是7cm、7cm.
因此其它两边长分别为7cm,7cm,
综上所述两边长分别为6cm,8cm或7cm,7cm.
【点评】本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.
考点2. 三角形的三条重要线段
4 .△ABC中BC边上的高作法正确的是( )
A.B.
C. D.
【分析】根据三角形高线的定义:过三角形的顶点向对边引垂线,顶点和垂足之间的线段叫做三角形的高线解答.
【解答】解:为△ABC中BC边上的高的是D选项.
故选:D.
【点评】本题考查了三角形的角平分线、中线、高线,熟记高线的定义是解题的关键.
5 .如图,ΔABC的面积为8cm,AP垂直ABC的平分线BP于P,则ΔPBC的面积为( )
A.2cm B.3cm C.4cm D.5cm
【答案】C
【解析】解:延长AP交BC于E,
∵AP垂直ABC的平分线BP于P,
∠ABP=∠EBP,∠APB=∠BPE=90°,
又∵BP=BP, ∴△ABP≌△BEP,
∴S△ABP=S△BEP,AP=PE,
∴△APC和△CPE等底同高,∴S△APC=S△PCE,
∴S△PBC=S△PBE+S△PCE=S△ABC=4cm2,故选:C.
如图,在中,、分别是的高和角平分线,.
(1)若,求的度数;
(2)试用、的代数式表示的度数_________.
【答案】(1);(2)
【解析】(1)解:,
,
是的平分线,.
是高线,,,
.
(2)解:,;,
是的平分线,.
是高线,,,
.
在△ABC中,AB=AC,DB为△ABC的中线,且BD将△ABC周长分为12cm与15cm两部分,求三角形各边长.
【分析】根据中线的定义得到AD=CD,设AD=CD=x,则AB=2x,分类讨论:当x+2x=12,BC+x=15;当x+2x=15,BC+x=12,然后分别求出x和BC,即可得到三角形三边的长.
【解答】解:如图,∵DB为△ABC的中线
∴AD=CD,
设AD=CD=x,则AB=2x,
当x+2x=12,解得x=4,
BC+x=15,解得BC=11,
此时△ABC的三边长为:AB=AC=8,BC=11;
当x+2x=15,BC+x=12,解得x=5,BC=7,
此时△ABC的三边长为:AB=AC=10,BC=7.
【点评】本题考查了三角形的角平分线、中线和高:三角形的一个顶点向底边作垂线,垂足与顶点之间的线段叫做三角形的高;三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线;三角形一边的中点与此边所对顶点的连线叫做三角形的中线.
考点三 三角形的角
如图,在中,是边上的高,是边上的高,、交于点,平分
(1)若,
①求的度数.
②若平分,试判断与的位置关系,并说明理由.
(2)设,则______(用含的代数式直接表示).
【答案】(1)①∠CFG;②FG∥AH;(2)180°-α
【解析】(1)解:①∵BD是AC边上的高,CE是AB边上的高,
∴∠CEA=∠ADB=90°,
∵∠BAC=56°,∠ACB=70°,∴∠ABC=180°-∠ACB-∠BAC=54°,
∴∠ABD=90°-∠BAC=34°,∠ACE=90°-∠BAC=34°,
∴∠FBG=∠ABC-∠ABD=20°,∠FCG=∠ACB-∠ACE=36°,
∴∠BFC=180°-∠DBC-∠FCG=124°,
∵FG平分∠BFC,∴∠CFG=;
②∵AH平分∠BAC,∴∠BAH=,
∴∠BHA=180°-∠HAB-∠ABH=98°,
在 BGF中,∠FGB=180°-∠FBG-∠BFG=98°,
∴FG∥AH;
(2)∵BD是AC边上的高,CE是AB边上的高,
∴∠CEA=∠ADB=90°,
∵∠BAC=α,∠ABC+∠ACB=180°-α,
∴∠ABD=90°-∠BAC=90°-α,∠ACE=90°-∠BAC=90°-α,
∴∠FBG+∠FCG=∠ABC+∠ACB-∠ABD-∠ACE=180°-α-(90°-α)-( 90°-α)= α,
∴∠BFC=180°-∠FBG-∠FCG =180°-α,
故答案为:180°-α.
9 .如图,在△ABC中,将CA沿DE翻折,点A落在F处,∠CEF、∠BDF、∠A三者之间的关系是( )
A.∠CEF=∠BDF+∠A B.∠CEF﹣3∠A=∠BDF
C.∠CEF=2(∠BDF+∠A) D.∠CEF﹣∠BDF=2∠A
【分析】根据三角形内角和定理可得∠CEF=∠A+∠AOE,∠AOE=∠F+∠BDF,从而可得∠CEF=∠A+∠F+∠BDF,由折叠性质可得∠A=∠F,从而可得∠CEF=2∠A+∠BDF,即可求解.
【解答】解:如图,
∵∠CEF=∠A+∠AOE,∠AOE=∠F+∠BDF,
∴∠CEF=∠A+∠F+∠BDF,
由折叠性质可得:
∠A=∠F,
∴∠CEF=2∠A+∠BDF,
∴∠CEF﹣∠BDF=2∠A,
故选:D.
【点评】本题考查三角形内角和定理,折叠的性质,解题的关键是正确利用△AOE和△DOF的内角和关系.
10 .如图1,AB与CD相交于点O,若,,和的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求:
(1)的度数;
(2)设,,,,其他条件不变,如图2,试问与、∠B之间存在着怎样的数量关系(用、表示),直接写出结论.
【答案】(1)33°;(2) .
【解析】解:(1)∵AP是∠DAB的角平分线,CP是∠DCB的角平分线
∴∠DAP=PAB,∠DCP=∠PCB
∵∠P+∠PAB=∠B+∠PCB,∠P+∠PCD=∠D+∠DAP
∴∠P+∠PAB+∠P+∠PCD=∠B+∠PCB+∠D+∠DAP
∴2∠P=∠B+∠D
∵∠B=28°,∠D=38°
∴∠P=33°
(2) ∠P=
∵∠P+∠PCD=∠D+∠DAP
∴∠PCD-∠DAP=∠D-∠P
∵∠D+∠DAO=∠B+∠OCB
∴∠DAB-∠DCB=∠B-∠D
∵,
∴∠DAB-∠DCB=3(∠DAP-∠DCP)
∴∠B-∠D=3(∠P-∠D)
∵,
∴∠P=
11.把直角三角形OAB与直角三角形O'CD如图1放置,直角顶点O与O′重合在一起,点D在OB上,∠B=30°,∠C=45°.现将△O'CD固定,△OAB绕点O顺时针旋转,旋转角α(0°≤α<90°),OB与DC交于点E.
(1)如图2,在旋转过程中,若OA∥CD时,则α= 45° ;若AB∥OC时,则α= 60° ;请写出证明过程.
(2)如图2,在旋转过程中,当△ODE有两个角相等时,α= 45°或67.5° ;请说明理由.
【分析】(1)利用平行线的性质求解即可;
(2)分两种情形:当∠D=∠DOE=45°时,当∠DOE=∠DEO=67.5°时,分别求解.
【解答】解:(1)当OA∥CD时,
∠AOD=∠D=45°,
∴α=45°,
当AB∥OC时,
∠AOD+∠A=90°,
∴∠AOD=30°,
∴α=60°,
故答案为:45°,60°.
(2)当∠D=∠DOE=45°时,α=45°,
当∠DOE=∠DEO=67.5°时,α=67.5°,
故答案为:45°或67.5°.
【点评】本题考查直角三角形的性质,三角形内角和定理等知识,解题的关键是学会由分类讨论的思想思考问题,属于中考常考题型.
考点四 多边形的内角和外角
12.阅读小明和小红的对话,解决下列问题.
(1)这个“多加的锐角”是 30 度.
(2)小明求的是几边形内角和?
(3)若这是个正多边形,则这个正多边形的一个内角是多少度?
【分析】(1)根据多边形内角和的计算方法进行估算即可;
(2)根据对话和多边形内角和的计算方法列方程求解即可;
(3)根据正多边形内角的计算方法进行计算即可.
【解答】解:(1)12边形的内角和为(12﹣2)×180°=1800°,而13边形的内角和为(13﹣2)×180°=1980°,
由于小红说“多边形的内角和不可能是1830°,你一定是多加了一个锐角”,
所以这个“多加的锐角”是1830°﹣1800°=30°,
故答案为:30;
(2)设这个多边形为n边形,由题意得,
(n﹣2)×180°=1800°,
解得n=12,
答:小明求的是12边形内角和;
(3)正十二边形的每一个内角为=150°,
答:这个正多边形的一个内角是150°.
【点评】本题考查多边形的内角和和外角和,掌握多边形内角和的计算方法以及正多边形的性质是正确解答的前提.
13.已知,如图,AD与BC交于点O.
(1)如图1,判断∠A+∠B与∠C+∠D的数量关系: ,并证明你的结论.
(2)如图2,∠A+∠B+∠C+∠D+∠E+∠F+∠M的度数为 .
(3)如图3,若CF平分∠BCD,DE平分∠ADC,CF与DE交于点M,∠E+∠F=50°,请直接写出∠A+∠B= .
【分析】(1)根据三角形内角和定理以及对顶角相等可得结论;
(2)利用(1)的结论以及五边形的内角和计算方法进行计算即可;
(3)利用角平分线的定义以及(1)的结论可得∠A+∠B=∠OCD+∠ODC=2(∠E+∠F)即可.
【解答】解:(1)∵∠AOB+∠A+∠B=180°=∠COD+∠C+∠D,∠AOB=∠COD,
∴∠A+∠B=∠C+∠D,
故答案为:∠A+∠B=∠C+∠D;
(2)如图2,连接AB,
由(1)得,∠OBA+∠OAB=∠C+∠D,
∴∠DAM+∠CBE+∠C+∠D+∠E+∠F+∠M的度数为五边形ABEFM的内角和,
即(5﹣2)×180°=540°,
故答案为:540°;
(3)∵CF平分∠BCD,DE平分∠ADC,
∴∠MCD=∠OCD,∠MDC=∠ODC,
由(1)可得,∠E+∠F=∠MCD+∠MDC,
∴∠OCD+∠ODC=50°,
∴∠OCD+∠ODC=100°,
∴∠A+∠B=∠OCD+∠ODC=100°,
故答案为:100°.
【点评】本题考查多边形的内角与外角,三角形内角和定理以及角平分线的定义,掌握三角形内角和是180°,角平分线的定义以及多边形内角和的计算方法是正确解答的前提.
如图,淇淇从点A出发,前进10米后向右转20°,再前进10米后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.
(1)求淇淇一共走了多少米?
(2)求这个多边形的内角和.
【分析】(1)第一次回到出发点A时,所经过的路线正好构成一个外角是20度的正多边形,求得边数,即可求解;
(2)根据多边形的内角和公式即可得到结论.
【解答】解:(1)∵所经过的路线正好构成一个外角是20度的正多边形,
∴360÷20=18,
18×10=180(米).
答:淇淇一共走了180米.
(2)根据题意,得(18﹣2)×180°=2880°,
答:这个多边形的内角和是2880°.
【点评】本题考查了正多边形的外角的计算以及多边形的内角和,第一次回到出发点A时,所经过的路线正好构成一个外角是20度的正多边形是关键.
针对练习
1.△ABC的周长为22cm,AB边比AC边长2cm,BC边是AC边的一半,求△ABC三边的长.
【分析】首先利用一个未知数表示出各边长,进而得出等式求出各边长即可.
【解答】解:设BC=x,则AC=2x,AB=2x+2,
∵AB+BC+AC=22,
∴2x+2x+2+x=22,
解得;x=4,
∴AC=8cm,BC=4cm,AB=10cm.
【点评】此题主要考查了三角形周长公式,根据题意得出关于三角形周长的方程是解题关键.
如图,AD是△ABC的高,CE是△ACB的角平分线,F是AC中点,∠ACB=50°,∠BAD=65°.
(1)求∠AEC的度数;
(2)若△BCF与△BAF的周长差为3,AB=7,则BC= 10 .
【分析】(1)根据三角形的高的概念得到∠ADB=90°,根据直角三角形的性质求出∠ABD,根据角平分线的定义求出∠ECB,根据三角形的外角性质计算即可;
(2)根据三角形的中线的概念得到AF=FC,根据三角形的周长公式计算,得到答案.
【解答】解:(1)∵AD是△ABC的高,
∴∠ADB=90°,
∵∠BAD=65°,
∴∠ABD=90°﹣65°=25°,
∵CE是△ACB的角平分线,∠ACB=50°,
∴∠ECB=∠ACB=25°,
∴∠AEC=∠ABD+∠ECB=25°+25°=50°;
(2)∵F是AC中点,
∴AF=FC,
∵△BCF与△BAF的周长差为3,
∴(BC+CF+BF)﹣(AB+AF+BF)=3,
∴BC﹣AB=3,
∵AB=7,
∴BC=10,
故答案为:10.
【点评】本题考查的是三角形的三角形的角平分线、中线和高,从三角形的一个顶点向对边作垂线,垂足与顶点之间的线段叫做三角形的高;三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线;三角形一边的中点与此边所对顶点的连线叫做三角形的中线.
3.如图已知:AD是△ABC的中线,AB=7cm,AD=5cm,△ABD的周长是18cm,
求BC的长.
【分析】根据三角形中线的定义得到BC=2BD,根据三角形周长公式即可得到结论.
【解答】解:∵AD是△ABC的中线,
∴BC=2BD,
∵AB=7cm,AD=5cm,△ABD的周长是18cm,
∴BD=18﹣7﹣5=6(cm),
∴BC的长为12cm.
【点评】本题考查了三角形的角平分线、中线和高,熟练掌握三角形中线的定义是解题的关键.
4.在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°.求∠BCD和∠ECD的度数.
【分析】由CD⊥AB与∠B=60°,根据两锐角互余,即可求得∠BCD的度数,又由∠A=20°,∠B=60°,求得∠ACB的度数,由CE是∠ACB的平分线,可求得∠ACE的度数,然后根据三角形外角的性质,求得∠CEB的度数.
【解答】解:∵CD⊥AB,
∴∠CDB=90°,
∵∠B=60°,
∴∠BCD=90°﹣∠B=90°﹣60°=30°;
∵∠A=20°,∠B=60°,∠A+∠B+∠ACB=180°,
∴∠ACB=100°,
∵CE是∠ACB的平分线,
∴∠ACE=∠ACB=50°,
∴∠CEB=∠A+∠ACE=20°+50°=70°,
∠ECD=90°﹣70°=20°.
或∠ECD=∠ECB﹣∠BCD=50°﹣30°=20°.
【点评】此题考查了三角形的内角和定理,三角形外角的性质以及三角形高线,角平分线的定义等知识.此题难度不大,解题的关键是数形结合思想的应用.
5.如图,在△ABC中,∠B=25°,∠BAC=31°,过点A作BC边上的高,交BC的延长线于点D,CE平分∠ACD,交AD于点E.
求:(1)∠ACD的度数;
(2)∠AEC的度数.
【分析】(1)利用三角形的外角的性质求解即可.
(2)求出∠ECD,∠D,利用三角形的外角的性质求解即可.
【解答】解:(1)∵∠ACD=∠B+∠BAC,∠B=25°,∠BAC=31°,
∴∠ACD=25°+31°=56°.
(2)∵AD⊥BD,
∴∠D=90°,
∵∠ACD=56°,CE平分∠ACD,
∴∠ECD=∠ACD=28°,
∴∠AEC=∠ECD+∠D=28°+90°=118°.
【点评】本题考查三角形内角和定理,三角形的外角的性质,角平分线的定义等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
6 .如图,点A、B、C、D是平面内四个点.连接AB、AC、BD、CD.
(1)如图1,求证:∠BDC=∠A+∠B+∠C;
(2)如图2,若BF平分∠ABD,CE平分∠ACD,BF与CE交于G,∠BDC=m°,∠BGC=n°,求∠A的度数.(用m,n表示)
【分析】(1)由三角形的外角性质,即可证明;
(2)由(1)的结论,即可求解.
【解答】(1)证明:延长BD交AC于E,
∵∠DEC=∠A+∠B,
∠BDC=∠DEC+∠C,
∴∠BDC=∠A+∠B+∠C,
(2)解:∵BF平分∠ABD,CE平分∠ACD,
∴∠DBG=∠ABF,∠DCG=∠ACE,
∵∠BDC=∠BGC+∠DBG+∠DCG,
∴∠DBG+∠DCG=∠BDC﹣∠BGC=m°﹣n°,
∴∠ABF+∠ACE=∠DBG+∠DCG=m°﹣n°,
∵∠BGC=∠A+∠ABF+∠ACE,
∴∠A=∠BGC﹣(∠ABF+∠ACE),
∴∠A=n°﹣(m°﹣n°)=2n°﹣m°.
【点评】本题考查三角形外角的性质,关键是掌握三角形外角的性质:三角形的一个外角等于和它不相邻的两个内角的和.
AD、BE为△ABC的高,AD、BE相交于H点,∠C=50°,求∠BHD.
【分析】根据同角的余角相等求出∠BHD=∠C,从而得解.
【解答】解:∵AD是△ABC的高,
∴∠BHD+∠HBD=90°,
∵BE是△ABC的高,
∴∠HBD+∠C=90°,
∴∠BHD=∠C,
∵∠C=50°,
∴∠BHD=50°.
【点评】本题考查了直角三角形两锐角互余的性质,同角的余角相等的性质,熟记性质并准确识图是解题的关键.
三角形具有稳定性,所以要使如图所示的五边形木架不变形,至少要钉上( )根木条.
A.1 B.2 C.3 D.4
【分析】三角形具有稳定性,所以要使五边形木架不变形需把它分成三角形,即过六边形的一个顶点作对角线,有几条对角线,就至少要钉上几根木条.
【解答】解:过五边形的一个顶点作对角线,有5﹣3=2条对角线,所以至少要钉上2根木条.
故选:B.
【点评】本题考查了三角形具有稳定性,是基础题,作出图形更形象直观
如图,已知四边形纸片ABCD的边AB∥CD,E是边CD上任意一点,沿BE折叠△BCE,点C落在点F的位置.
(1)如图①,点F落在四边形ABED的内部,探索∠FED,∠ABF,∠C之间的数量关系,并说明理由;
(2)如图②,点F落在边CD的上方,设BF与CD交于点N,直接写出∠FED,∠ABF,∠C之间的数量关系,不需要说明理由.
【分析】(1)数量关系:∠FED+∠ABF=∠C.理由:过点F作MN∥CD,交AD于点M,交BC于点N,由平行线的性质可得∠FED=∠EFN,根据平行公理的推论可得MN∥AB,继而得到∠NFB=∠ABF,再结合折叠的性质可得数量关系.
(2)过点F作GH∥CD,由平行线的性质可得∠FED=∠HFE,根据平行公理的推论可得GH∥AB,继而得到得∠ABF=∠HFB,再结合折叠的性质可得数量关系.
【解答】解:(1)∠FED,∠ABF,∠C 之间的数量关系:∠FED+∠ABF=∠C.
理由如下:如图①,过点F作MN∥CD,交AD于点M,交BC于点N
则∠FED=∠EFN,
∵AB∥CD,
∴MN∥AB,
∴∠NFB=∠ABF,
∴∠FED+∠ABF=∠EFN+∠NFB=∠EFB,
由折叠的性质得,△BCE≌△BFE,
∴∠EFB=∠C,
∴∠FED+∠ABF=∠C,
∴∠FED,∠ABF,∠C 之间的数量关系是:∠FED+∠ABF=∠C.
(2)如图②,过点F作GH∥CD
则∠FED=∠HFE,
∵AB∥CD,
∴GH∥AB,
∴∠ABF=∠HFB=∠HFE+∠BFE=∠FED+∠BFE,
由折叠的性质得,△BCE≌△BFE,
∴∠BFE=∠C,
∴∠ABF=∠FED+∠C,即∠ABF﹣∠FED=∠C,
∴∠FED,∠ABF,∠C 之间的数量关系是:∠ABF﹣∠FED=∠C.
【点评】本题考查折叠的性质,平行线的性质,平行公理的推论.掌握折叠的性质和平行线的性质是解题的关键.
10 .利用图形这一直观性语言,在一定程度上可以降低我们认识和理解抽象逻辑推理的难度;利用图形建构几何直观,可以轻松实现空间形式和数量关系的相互转化.让我们在如下的问题解决中体验一下吧!
【模块探究】
如图1,求证:∠BOC=∠A+∠B+∠C
【直观应用】
(1)应用上述结论,若图2中,∠EOF=α,则∠A、∠B、∠C、∠D、∠E、∠F的度数之和等于 2α (直接给出结论,不必说明理由)
(2)应用上述结论,求图3所示的五角星中,∠A、∠B、∠C、∠D、∠E的度数之和是多少?证明你的结论;
【类比联系】
如图4,求∠A、∠B、∠C、∠D、∠E、∠F、∠G的度数之和是多少?证明你的结论.
【分析】模块探究,由三角形外角的性质,即可证明;
直观应用,应用模块探究的结论,即可解决问题;
类比联系,应用模块探究的结论,即可解决问题.
【解答】
模块探究,证明:延长BO交AC于D,
∵∠BOC=∠C+∠CDO,∠CDO=∠A+∠B,
∴∠BOC=∠A+∠B+∠C;
直观应用,解:(1)由上述结论得:∠BOC=∠A+∠B+∠C,∠EOF=∠D+∠E+∠F,
∴∠A+∠B+∠C+∠D+∠E+∠F=∠BOC+∠EOF=2α,
故答案为:2α.
(2)∠A、∠B、∠C、∠D、∠E的度数之和是180°,
证明:∵∠BOC=∠A+∠B+∠C,∠COD=∠E+∠D,
∴∠A+∠B+∠C+∠E+∠D=∠BOC+∠COD=180°;
类比联系:∵∠DMN=∠G+∠GNM,∠GNM=∠BNC=∠F+∠B+∠C,
∴∠DMN=∠G+∠F+∠B+∠C,
∵∠EMD=∠A+∠E+∠D
∴∠A+∠E+∠D+=∠G+∠F+∠B+∠C=∠EMD+∠DMN=180°.
【点评】本题考查角的计算,关键是注意应用题目中的结论.
11 .如图,AB⊥CD,垂足为O,点P、Q分别在射线OC、OA上运动(点P、Q都不与点O重合),QE是∠AQP的平分线.
(1)如图1,在点P、Q的运动过程中,若直线QE交∠DPQ的平分线于点H.
①当∠PQB=60°时,∠PHE= 45 °;
②随着点P、Q分别在OC、OA的运动,∠PHE的大小是否是定值?如果是定值,请求出∠PHE的度数;如果不是定值,请说明理由;
(2)如图2,若QE所在直线交∠QPC的平分线于点E时,将△EFG沿FG折叠,使点E落在四边形PFGQ内点E′的位置,猜测∠PFE′与∠QGE′之间的数量关系,并说明理由.
【分析】(1)①先根据垂直的定义求出∠POQ=90°,即可利用三角形内角和定理和邻补角的定义求出∠QPO=30°,∠AQP=120°,再由角平分线的定义分别求出∠EQP=60°,∠HPQ=15°,最后根据三角形外角的性质求解即可;②同①方法求解即可;
(2)如图所示,连接EE',先求出∠CPQ+∠PQA=270°,再由角平分线的定义求出∠EPQ+∠EQP=135°,则∠PEQ=45°,由折叠的性质可知∠GE'F=∠PEQ=45°,进而推出∠EFE'+∠EFE'=270°即可得到答案.
【解答】解:(1)①∵AB⊥CD,
∴∠POQ=90°,
∴∠PQO+∠QPO=90°,
∵∠PQB=60°,
∴∠QPO=30°,∠AQP=120°,
∵EQ平分∠AQP,PH平分∠QPO,
∴,,
∴∠H=∠EQP﹣∠HPQ=45°,
故答案为:45;
②∠PHE 是一个定值,∠PHE=45°,理由如下:
∵AB⊥CD,
∴∠POQ=90°,
∴∠PQO+∠QPO=90°,
∴∠QPO=90°﹣∠PQO,∠AQP=180°﹣∠PQO,
∵EQ平分∠AQP,PH平分∠QPO,
∴,,
∴∠H=∠EQP﹣∠HPQ=45°;
(2)∠PFE'+∠QGE'=90°,理由如下:
如图2所示,连接EE',
∵AB⊥CD,
∴∠POQ=90°,
∴∠PQO+∠QPO=90°,
∵∠CPQ+∠QPO=180°,∠PQA+∠PQO=180°,
∴180°﹣∠CPQ+180°﹣∠PQA=90°,
∴∠CPQ+∠PQA=270°,
∵QE,PE分别平分∠PQA,∠CPQ,
∴,
∴,
∴∠PEQ=180°﹣∠EPQ﹣∠EQP=45°,
由折叠的性质可知∠GE'F=∠PEQ=45°,
∵∠FEE'+∠EFE'+∠EE'F=180°=∠GEE'+∠EGE'+∠EE'G,
∴∠FEG+∠FE'G+∠EFE'+∠EGE'=360°,
∴∠EFE'+∠EFE'=270°,
∵∠EFE'+∠PFE'=180°=∠EGE'+∠QGE',
∴∠PFE'+∠QGE'=360°﹣∠EFE'﹣∠EFE'=90°.
【点评】本题主要考查了三角形内角和定理,三角形外角的性质,角平分线的定义,邻补角,熟知三角形内角和定理和角平分线的定义是解题的关键
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
