八年级数学上分层优化堂堂清(12)第十一章 三角形 综合素质测评(含解析)
文档属性
| 名称 | 八年级数学上分层优化堂堂清(12)第十一章 三角形 综合素质测评(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
八年级数学上分层优化堂堂清
十一章 三角形
本章综合素质测评
时间90分钟满分120分
填空题(每小题3分,共30分)
1.已知三角形两边的长分别是3和7,则此三角形第三边的长可能是( )
A.1 B.2 C.8 D.11
2.如图,工人师傅砌门时,常用木条固定长方形门框,使其不变形,这样做的根据是( )
A.两点之间的线段最短
B.长方形的四个角都是直角
C.长方形是轴对称图形
D.三角形有稳定性.
3 .在直角三角形中,有一个锐角为52°,那么另一个锐角的度数( )
A.30° B.48° C.38° D.52°
4.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7 B.7或8 C.8或9 D.7或8或9
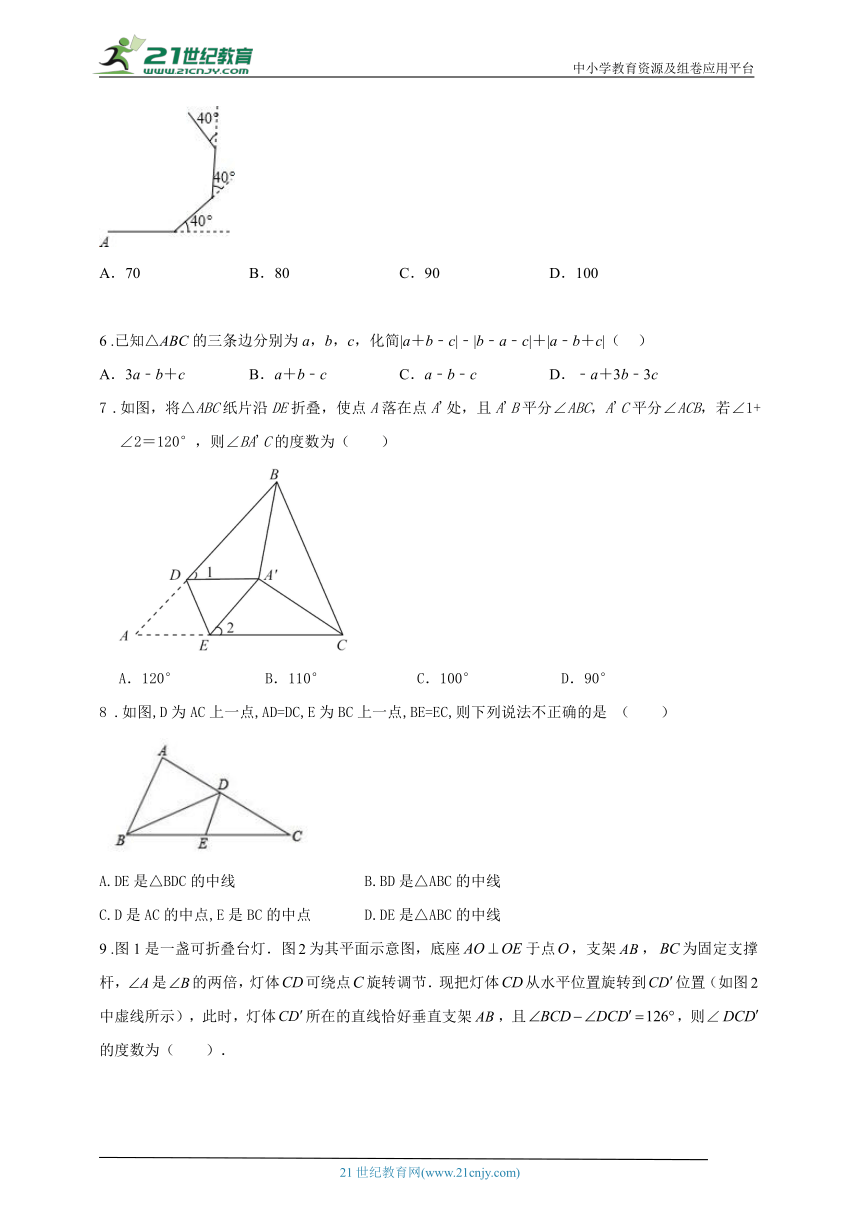
5 .如图,小明在操场上从A点出发,沿直线前进10米后向左转,再沿直线前进10米后,又向左转,这样走下去,他第一次回到出发地A点时,一共走了( )米
A.70 B.80 C.90 D.100
6 .已知△ABC的三条边分别为a,b,c,化简|a+b﹣c|﹣|b﹣a﹣c|+|a﹣b+c|( )
A.3a﹣b+c B.a+b﹣c C.a﹣b﹣c D.﹣a+3b﹣3c
7 .如图,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠1+∠2=120°,则∠BA'C的度数为( )
A.120° B.110° C.100° D.90°
8 .如图,D为AC上一点,AD=DC,E为BC上一点,BE=EC,则下列说法不正确的是 ( )
A.DE是△BDC的中线 B.BD是△ABC的中线
C.D是AC的中点,E是BC的中点 D.DE是△ABC的中线
9 .图1是一盏可折叠台灯.图为其平面示意图,底座于点,支架,为固定支撑杆,是的两倍,灯体可绕点旋转调节.现把灯体从水平位置旋转到位置(如图中虚线所示),此时,灯体所在的直线恰好垂直支架,且,则∠的度数为( ).
A. B. C. D.
10 .如图,在△ABC中,∠A=90°,BE,CD分别平分∠ABC和∠ACB,且相交于F,,于点G,则下列结论 ①∠CEG = 2∠DCA;②CA平分∠BCG;③∠ADC =∠GCD;④∠DFB=∠A;⑤∠DFE=135°,其中正确的结论是( )
A.①②③ B.①③④ C.①③④⑤ D.①②③④
填空题(每小题3分,共15分)
11 .已知三角形的两边长分别为和,则第三边的取值范围_____.
12 .如图,在中,,是斜边的中点,将沿直线折叠,点落在点处,如果恰好与垂直,则_______°.
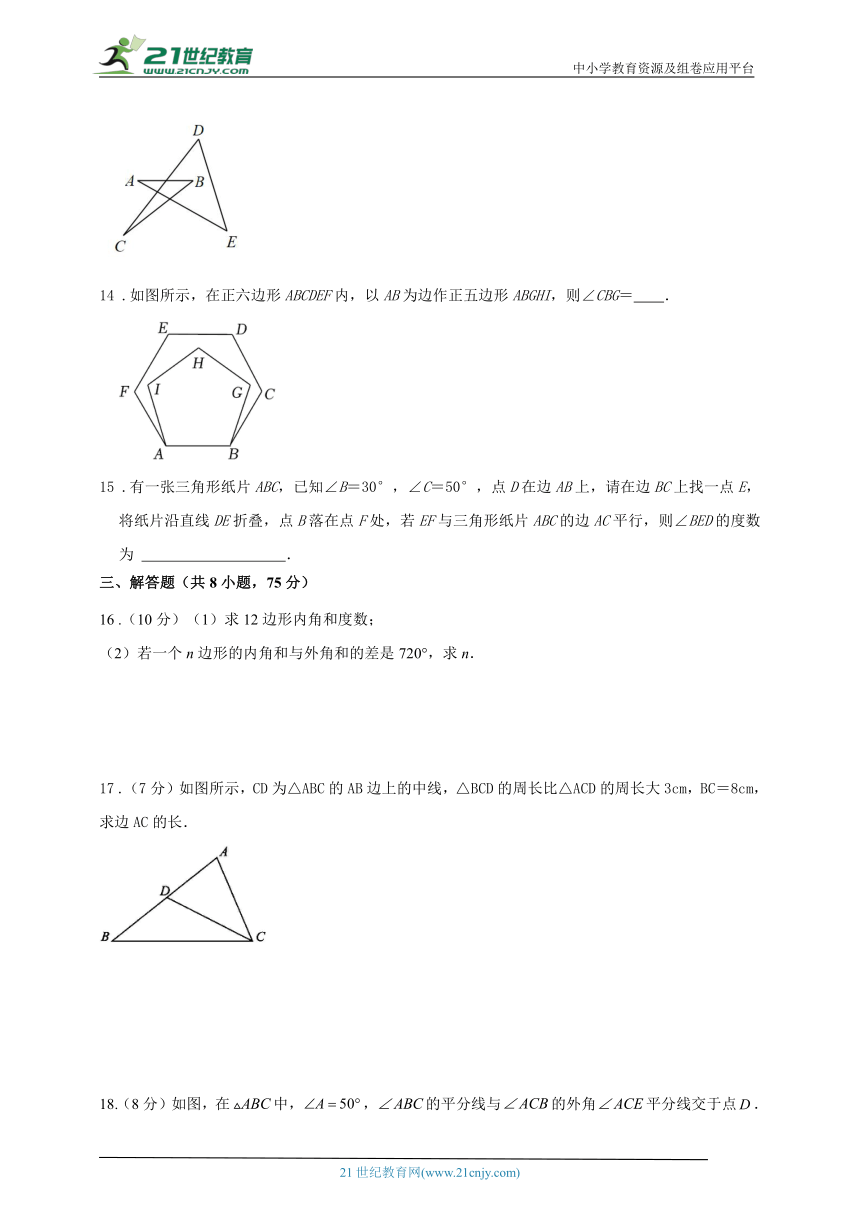
13 .如图,的度数为______度.
14 .如图所示,在正六边形ABCDEF内,以AB为边作正五边形ABGHI,则∠CBG= .
15 .有一张三角形纸片ABC,已知∠B=30°,∠C=50°,点D在边AB上,请在边BC上找一点E,将纸片沿直线DE折叠,点B落在点F处,若EF与三角形纸片ABC的边AC平行,则∠BED的度数为 .
解答题(共8小题,75分)
16 .(10分)(1)求12边形内角和度数;
(2)若一个n边形的内角和与外角和的差是720°,求n.
17 .(7分)如图所示,CD为△ABC的AB边上的中线,△BCD的周长比△ACD的周长大3cm,BC=8cm,求边AC的长.
18.(8分)如图,在中,,的平分线与的外角平分线交于点.
(1)求的度数;
(2)你能说出与之间存在怎样的数量关系吗?
19 .(8分)如图,在中,是高,、是角平分线,它们相交于点,.
(1)的度数为______;
(2)若,求的度数.
20 .(9分)已知:线段AB,CD相交于点O,连接AD,CB,和的平分线AP和CP相交于点P,与CD,AB相交于M,N,如图2:
(1)在图1中,直接写出,,,之间的数量关系;
(2)图中有几个八字模型?
(3)在图2中,与为任意角,试探究与,之间是否存在一定的数量关系,若存在,请写出它们之间的数量关系并证明;若不存在,请说明理由
21 .(8分)【教材呈现】如图是华师版七年级下册数学教材第76页的部分内容如图.
如图,分别用、、表示的三个内角,证明.
延长至点,以点为顶点,在的上侧作,则(同位角相等,两直线平行).
(1)请根据教材提示,结合图①,将证明过程补充完整.
【结论应用】
(2)如图②,在中,,平分,平分,求的度数.
22 .(12分)在和(共边且不重合)中,,.
(1)如图1,当和均为钝角三角形,在直线两侧时,和之间的数量关系为______.
(2)如图2,当和均为锐角三角形,且在直线两侧时,和之间的数量关系为______.
(3)如图3,当为钝角三角形,为锐角三角形,且在直线同侧时,求证:.
(4)分别作和的角平分线,两条角平分线所在直线交于点(点不与点或者点重合),当时,直接写出的度数.
23 .(13分)如图,在△ABC中,点D在AB上,过点D作DE∥BC,交AC于点E,DP平分∠ADE,交∠ACB的平分线于点P,CP与DE相交于点G,∠ACF的平分线CQ与DP相交于点Q.
(1)若∠A=50°,∠B=60°,则∠DPC= °,∠Q ;
(2)若∠A=50°,当∠B的度数发生变化时,∠DPC、∠Q的度数是否发生变化?并说明理由;
(3)若△PCQ中存在一个内角等于另一个内角的三倍,请直接写出所有符合条件的∠A的度数 .
八年级数学上分层优化堂堂清
十一章 三角形
本章综合素质测评(解析版)
时间90分钟满分120分
填空题(每小题3分,共30分)
1.已知三角形两边的长分别是3和7,则此三角形第三边的长可能是( )
A.1 B.2 C.8 D.11
【答案】C.
【解析】根据三角形的三边关系可得7﹣3<x<7+3,再解即可.
设三角形第三边的长为x,由题意得:7﹣3<x<7+3,
4<x<10,故选C
2.如图,工人师傅砌门时,常用木条固定长方形门框,使其不变形,这样做的根据是( )
A.两点之间的线段最短
B.长方形的四个角都是直角
C.长方形是轴对称图形
D.三角形有稳定性
【答案】D
【分析】根据三角形的稳定性,即可求解.
【详解】解:根据题意得:用木条固定长方形门框,使其不变形,这样做的根据是三角形有稳定性.
故选:D
【点评】本题主要考查三角形的稳定性,三角形的稳定性有着稳固、坚定、耐压的特点,因此题中用木条固定门框,使其不变形.
3 .在直角三角形中,有一个锐角为52°,那么另一个锐角的度数( )
A.30° B.48° C.38° D.52°
【答案】C
【分析】根据直角三角形的两个锐角互余即可求得.
【详解】解:由题意可得,
另一个锐角度数为:90°-52°=38°,
故选C.
【点评】本题考查了直角三角形的性质,解决本题的关键是直角三角形的两个锐角互余.
4.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7 B.7或8 C.8或9 D.7或8或9
【答案】D.
【解析】本题考查了多边形的内角和定理,一个多边形截去一个角后它的边数可能增加1,可能减少1,或不变.
首先求得内角和为1080°的多边形的边数,即可确定原多边形的边数.
设内角和为1080°的多边形的边数是n,则(n﹣2) 180°=1080°,
解得:n=8.
则原多边形的边数为7或8或9.
5 .如图,小明在操场上从A点出发,沿直线前进10米后向左转,再沿直线前进10米后,又向左转,这样走下去,他第一次回到出发地A点时,一共走了( )米
A.70 B.80 C.90 D.100
【答案】C
【分析】利用多边形的外角和得出小明回到出发地A点时左转的次数,即可解决问题.
【详解】解:由题意可知,小明第一次回到出发地A点时,他一共转了360°,且每次都是向左转40°,
所以共转了9次,一次沿直线前进10米,9次就前进90米.
故选:C.
【点评】本题考查根据多边形的外角和解决实际问题,注意多边形的外角和是360°.
6 .已知△ABC的三条边分别为a,b,c,化简|a+b﹣c|﹣|b﹣a﹣c|+|a﹣b+c|( )
A.3a﹣b+c B.a+b﹣c C.a﹣b﹣c D.﹣a+3b﹣3c
【答案】B
【分析】根据三角形的任意两边之和大于第三边可得a+b c>0,a b+c>0,b a c<0,再根据绝对值的性质去掉绝对值符号,然后利用整式的加减运算进行计算即可得解.
【详解】解:∵a、b、c分别为△ABC的三边长,
∴a+b c>0,b a c<0,a b+c>0,
∴|a+b c| |b a c|+|a b+c|
=a+b c (a+c b)+a b+c
=a+b c a c+b+a b+c
=a+b c.
故选:B.
7 .如图,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠1+∠2=120°,则∠BA'C的度数为( )
A.120° B.110° C.100° D.90°
解:∵∠BDE、∠CED是△ADE的两个外角,
∴∠BDE=∠A+∠AED,∠CED=∠A+∠ADE,
∴∠BDE+∠CED=∠A+∠AED+∠A+∠ADE,
∴∠1+∠ADE+∠2+∠AED=2∠A+∠AED+∠ADE,
即∠1+∠2=2∠A,
∵∠1+∠2=120°,
∴∠A=60°,
∵BA'平分∠ABC,CA'平分∠ACB,
∴∠A'BC+∠A'CB=(∠ABC+∠ACB)
=(180°﹣∠A)
=90°﹣∠A.
∴∠BA'C=180°﹣(∠A'BC+∠A'CB),
=180°﹣(90°﹣∠A)
=90°+∠A
=90°+×60°
=120°.
故选:A.
8 .如图,D为AC上一点,AD=DC,E为BC上一点,BE=EC,则下列说法不正确的是 ( )
A.DE是△BDC的中线 B.BD是△ABC的中线
C.D是AC的中点,E是BC的中点 D.DE是△ABC的中线
【答案】D
【解析】A.点E是BC的中点,所以DE是△BDC的中线,故A正确,与要求不相符;
B.因为D是△ABC的边AC的中点,所以BD是AC边的中线,故B正确,与要求不相符;
C.由D,E分别是△ABC的边AC,BC的中点可知AD=DC,BE=EC,故C正确,与要求不相符;
D.由三角形的中线的定义可知DE不是△ABC的中线,故D错误,与要求相符.故选D.
9 .图1是一盏可折叠台灯.图为其平面示意图,底座于点,支架,为固定支撑杆,是的两倍,灯体可绕点旋转调节.现把灯体从水平位置旋转到位置(如图中虚线所示),此时,灯体所在的直线恰好垂直支架,且,则∠的度数为( ).
A. B. C. D.
【答案】B
【分析】延长交于点,延长交于点,则,得到,在四边形中,利用四边形的内角和为,列出等式,即可求出的度数.
【详解】解:延长交于点,延长交于点,如图:
,,
,
,,
,
,
,
,
,
,
,
,
在四边形中,有
,
,
解得:;
故选:B.
【点评】本题考查了四边形的内角和的应用,同角的补角相等,邻补角的定义,几何图形中角度的和差关系,解题的关键是正确的作出辅助线,利用四边形的内角和为进行解题.
10 .如图,在△ABC中,∠A=90°,BE,CD分别平分∠ABC和∠ACB,且相交于F,,于点G,则下列结论 ①∠CEG = 2∠DCA;②CA平分∠BCG;③∠ADC =∠GCD;④∠DFB=∠A;⑤∠DFE=135°,其中正确的结论是( )
A.①②③ B.①③④ C.①③④⑤ D.①②③④
【答案】C
【分析】根据平行线的性质与角平分线的定义即可判断①;只需要证明∠ADC+∠ACD=90°,∠GCD+∠BCD=90°,即可判断③;根据角平分线的定义和三角形内角和定理先推出,即可判断④⑤;根据现有条件无法推出②.
【详解】解:∵CD平分∠ACB,
∴∠ACB=2∠DCA,∠ACD=∠BCD
∵,
∴∠CEG=∠ACB=2∠DCA,故①正确;
∵∠A=90°,CG⊥EG,,
∴∠ADC+∠ACD=90°,CG⊥BC,即∠BCG=90°,
∴∠GCD+∠BCD=90°,
又∵∠BCD=∠ACD,
∴∠ADC=∠GDC,故③正确;
∵∠A=90°,
∴∠ABC+∠ACB=90°,
∵BE,CD分别平分∠ABC,∠ACB,
∴,
∴,
∴∠DFB=180°-∠BFC=45°,
∴,故④正确;
∵∠BFC=135°,
∴∠DFE=∠BFC=135°,故⑤正确;
根据现有条件,无法推出CA平分∠BCG,故②错误;
故选C.
【点评】本题主要考查了平行线的性质,角平分线的定义,三角形内角和定理,熟知平行线的性质,角平分线的定义是解题的关键.
填空题(每小题3分,共15分)
11 .已知三角形的两边长分别为和,则第三边的取值范围_____.
【答案】
【分析】设第三边为,根据三角形的三边关系列出不等式即可得到答案.
【详解】解:设第三边为,
已知三角形的两边长分别为和,则第三边的取值范围是,即,
故答案为:.
【点评】本题考查三角形三边关系,熟记三角形三边关系:任意两边之和大于第三边、任意两边之差小于第三边是解决问题的关键.
12 .如图,在中,,是斜边的中点,将沿直线折叠,点落在点处,如果恰好与垂直,则_______°.
【答案】30
【分析】根据折叠的性质可知,折叠前后的两个三角形全等,则 ,从而求得答案.
【详解】解:如图,
在中,,
∵是斜边上的中线,
∴,
∴,
将沿直线折叠,点落在点处,
设度,
∵,
∴,
如果恰好与垂直,
在中,,
即,
解得, ,
∴,
∵,
∴,
即
故答案为:30
【点评】本题考查图形的折叠变化及三角形的内角和定理.关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.
13 .如图,的度数为______度.
【答案】
【分析】如图,交于点,交于点,利用外角的性质,得到:进而得到:,即可得解.
【详解】解:如图,交于点,交于点,
则:,
∴.
故答案为:.
【点评】本题考查三角形外角的性质和三角形的内角和定理.熟练掌握三角形的一个外角等于与它不相邻的两个内角和,以及三角形的内角和定理,是解题的关键.
14 .如图所示,在正六边形ABCDEF内,以AB为边作正五边形ABGHI,则∠CBG= .
解:在正六边形ABCDEF内,正五边形ABGHI中,∠ABC=120°,∠ABG=108°,
∴∠CBG=∠ABC﹣∠ABG=120°﹣108°=12°.
故答案为:12°.
15 .有一张三角形纸片ABC,已知∠B=30°,∠C=50°,点D在边AB上,请在边BC上找一点E,将纸片沿直线DE折叠,点B落在点F处,若EF与三角形纸片ABC的边AC平行,则∠BED的度数为 .
解:①当点F在AB的上方时,如图:
∵AC∥EF,∠C=50°,
∴∠BEF=∠C=50°,
∴∠BED=∠FED=∠BEF=×50°=25°;
②当点F在BC的下方时,如图:
∵AC∥EF,∠C=50°,
∴∠CEF=∠C=50°,
∵∠F=∠B=30°,
∴∠BGD=50°+30°=80°,
∴∠BDG=180°﹣80°﹣30°=70°,
∴∠BDE=∠BDG=×70°=35°;
∴∠BED=180°﹣∠B﹣∠BDE=180°﹣30°﹣35°=115°
综上所述,∠BDE的度数为25°或115°.
故答案为:25°或115°.
解答题(共8小题,75分)
16 .(10分)(1)求12边形内角和度数;
(2)若一个n边形的内角和与外角和的差是720°,求n.
【答案】(1)1800°;(2)8
【分析】(1)根据内角和公式,可得答案;
(2)根据多边形内角和公式(n-2) 180°可得内角和,再根据外角和为360°可得方程(n-2) 180°-360°=720°,再解方程即可.
【详解】解:(1)由题意,得
(12-2)×180°=1800°;
(2)由题意得:
(n-2) 180°-360°=720°,
解得:n=8.
【点睛】此题主要考查了多边形的内角和和外角和,解题的关键是掌握多边形的内角和公式与外角和定理.
17 .(7分)如图所示,CD为△ABC的AB边上的中线,△BCD的周长比△ACD的周长大3cm,BC=8cm,求边AC的长.
【答案】AC的长为5cm.
【解析】根据题意,结合图形,有下列数量关系:①AD=BD,②△BCD的周长比△ACD的周长大3.
依题意:△BCD的周长比△ACD的周长大3cm,
故有:BC+CD+BD-(AC+CD+AD)=3.
又∵ CD为△ABC的AB边上的中线,
∴ AD=BD,即BC-AC=3.
又∵ BC=8,∴ AC=5.
18.(8分)如图,在中,,的平分线与的外角平分线交于点.
(1)求的度数;
(2)你能说出与之间存在怎样的数量关系吗?
【答案】(1)
(2)
【分析】(1)由角平分线的定义可得,,由三角形的外角性质可得:,,再结合,从而可求解;
(2)令,结合(1)的解答过程进行判断即可.
【详解】(1)解:如图所示:
的平分线与的外角平分线交于点,
,,
是的外角,也是的外角,
,,
则有,
是的外角,
,
,
,
即,
得;
(2)当时,
的平分线与的外角平分线交于点,
,,
是的外角,也是的外角,
,,
则有,
是的外角,
,
,
,
即,
.
【点评】本题主要考查三角形的外角性质,角平分线的定义,解答的关键是结合图形,分析清楚各角之间的关系.
19 .(8分)如图,在中,是高,、是角平分线,它们相交于点,.
(1)的度数为______;
(2)若,求的度数.
【答案】(1)
(2)
【分析】(1)根据角平分线的定义得出,根据三角形内角和定理得出,进而即可求解;
(2)根据三角形内角和定理求得,根据是的角平分线,得出,根据 ,即可求解.
【详解】(1)解:∵、是、的角平分线,
∴,
在中,,
∴,
∴,
故答案为:;
(2)解:∵在中,是高,,,
∴,
∵是的角平分线,
∴,
∴ ,
∴.
【点评】本题考查了三角形中线,角平分线,三角形内角和定理,掌握三角形内角和定理是解题的关键.
20 .(9分)已知:线段AB,CD相交于点O,连接AD,CB,和的平分线AP和CP相交于点P,与CD,AB相交于M,N,如图2:
(1)在图1中,直接写出,,,之间的数量关系;
(2)图中有几个八字模型?
(3)在图2中,与为任意角,试探究与,之间是否存在一定的数量关系,若存在,请写出它们之间的数量关系并证明;若不存在,请说明理由
【答案】(1);(2)6个;(3),证明见详解.
【分析】(1)根据三角形内角和定理即可求解;
(2)可以以三角形的公共点为中心寻找;
(3)利用(1)中所得到得结论,列出两组关系式,然后结合角平分线性质即可得证;
【详解】(1) 在和中:
, ,且
(2)一共有6组,分别是:和,和,和,和,和,和;
(3) ,证明如下:
由(1)得:
又 和分别是和的平分线
【点评】本题主要考查了三角形的“8”字模型,充分理解“8”字模型的结论,并利用它进行角度的计算是解决本题的关键.
21 .(8分)【教材呈现】如图是华师版七年级下册数学教材第76页的部分内容如图.
如图,分别用、、表示的三个内角,证明.
延长至点,以点为顶点,在的上侧作,则(同位角相等,两直线平行).
(1)请根据教材提示,结合图①,将证明过程补充完整.
【结论应用】
(2)如图②,在中,,平分,平分,求的度数.
【答案】(1)见详解
(2)
【分析】(1)利用平行线的性质得,即可解答;
(2)利用角平分线的定义和三角形内角和定理可得;
【详解】(1)由题意得:,,
两直线平行,内错角相等,
,
即.
(2),分别平分和,
,,
,
,
,
.
【点评】本题主要考查了平行线的性质,角平分线的定义,三角形内角和定理等知识,熟练掌握平行线的性质,是解题的关键.
22 .(12分)在和(共边且不重合)中,,.
(1)如图1,当和均为钝角三角形,在直线两侧时,和之间的数量关系为______.
(2)如图2,当和均为锐角三角形,且在直线两侧时,和之间的数量关系为______.
(3)如图3,当为钝角三角形,为锐角三角形,且在直线同侧时,求证:.
(4)分别作和的角平分线,两条角平分线所在直线交于点(点不与点或者点重合),当时,直接写出的度数.
【答案】(1)
(2)
(3)见解析
(4)
【分析】(1)根据三角形的外角的性质定理即可求解;
(2)根据多边形的内角和的公式即可求解;
(3)根据三角形的外角和定理,角的等量代换即可求解;
(4)根据题意,结合(1)、(2)、(3)的结论,角平分线的性质,三角形的内角和定理,外角和定理,分类讨论,由此即可求解.
【详解】(1)解:如图所示,延长,
在,中,,,
∵,,,
∴,
∴,
故答案为:.
(2)解:根据四边形的内角和可知,,
∵,,
∴,
∴,
∴,
故答案为:.
(3)证明:如图所示,设交于点,
∵在中,,在中,,
∴,
又∵,,
∴
,
∵,
∴.
(4)解:①如图所示,,分别是的平分线,,
∴,,
∵,,
∴,
∴,
由(1)可知,,
∴,
∴;
②如图所示,,分别是的平分线,,且,,
∴,,
∴,
由(2)可知,,
∴,
在四边形中,根据四边形内角和可得,;
③如图所示,,分别是的平分线,,设交于点,
在中,,在中,,
∴,
∴,
∵,,
∴,
∴,
由(3)可知,,
∴,
∴;
综上所示,的度数为.
【点评】本题主要考查等腰三角形的性质,三角形的内角和定理,外角和定理,四边形的内角和定理,角平分线的性质的综合,掌握以上知识的综合运用是解题的关键.
23 .(13分)如图,在△ABC中,点D在AB上,过点D作DE∥BC,交AC于点E,DP平分∠ADE,交∠ACB的平分线于点P,CP与DE相交于点G,∠ACF的平分线CQ与DP相交于点Q.
(1)若∠A=50°,∠B=60°,则∠DPC= °,∠Q ;
(2)若∠A=50°,当∠B的度数发生变化时,∠DPC、∠Q的度数是否发生变化?并说明理由;
(3)若△PCQ中存在一个内角等于另一个内角的三倍,请直接写出所有符合条件的∠A的度数 .
解:(1)∵∠A=50°,∠B=60°,
∴∠ACB=70°,
∴∠BCP=∠ACB=35°,
∵DE∥BC,
∴∠ADE=∠B=60°,∠PGD=∠PCB=35°,
∵∠PDE=∠ADE=30°,
∴∠DPC=180°﹣∠PDE﹣∠PGD=115°;
又∵∠ACQ=∠ACF,
∴∠PCQ=∠ACQ+∠ACP=(∠ACF+∠ACB)=90°,
∴∠Q=∠DPC﹣∠QCP=25°;
故答案为:115,25;
(2)∠DPC、∠Q的度数不会发生变化.
理由:由(1)得:∵∠PDE=∠ADE=∠B,∠PGD=∠BCP=∠ACB,
∴∠DPC=180°﹣∠PDE﹣∠PGD=180°﹣∠B﹣∠ACB=180°﹣(∠B+∠ACB)=180°﹣(180°﹣∠A)=90°+∠A=115°;
∴∠Q=∠DPC﹣∠QCP=25°;
(3)设∠A=x,则,
∵CP平分∠ACB,CQ平分∠ACF,
∴,,
∴,,
因为△PCQ中存在一个内角等于另一个内角的三倍,
∴①当∠Q=3∠QPC时,,
∴x=135°,
②当∠QPC=3∠Q时,,
∴x=45°,
③当∠PCQ=3∠Q时,,
∴x=60°,
④当∠PCQ=3∠QPC时,,
∴x=120°,
综上①②③④可知∠A=45°或60°或120°或135°.
故答案为:45°或60°或120°或135°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
八年级数学上分层优化堂堂清
十一章 三角形
本章综合素质测评
时间90分钟满分120分
填空题(每小题3分,共30分)
1.已知三角形两边的长分别是3和7,则此三角形第三边的长可能是( )
A.1 B.2 C.8 D.11
2.如图,工人师傅砌门时,常用木条固定长方形门框,使其不变形,这样做的根据是( )
A.两点之间的线段最短
B.长方形的四个角都是直角
C.长方形是轴对称图形
D.三角形有稳定性.
3 .在直角三角形中,有一个锐角为52°,那么另一个锐角的度数( )
A.30° B.48° C.38° D.52°
4.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7 B.7或8 C.8或9 D.7或8或9
5 .如图,小明在操场上从A点出发,沿直线前进10米后向左转,再沿直线前进10米后,又向左转,这样走下去,他第一次回到出发地A点时,一共走了( )米
A.70 B.80 C.90 D.100
6 .已知△ABC的三条边分别为a,b,c,化简|a+b﹣c|﹣|b﹣a﹣c|+|a﹣b+c|( )
A.3a﹣b+c B.a+b﹣c C.a﹣b﹣c D.﹣a+3b﹣3c
7 .如图,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠1+∠2=120°,则∠BA'C的度数为( )
A.120° B.110° C.100° D.90°
8 .如图,D为AC上一点,AD=DC,E为BC上一点,BE=EC,则下列说法不正确的是 ( )
A.DE是△BDC的中线 B.BD是△ABC的中线
C.D是AC的中点,E是BC的中点 D.DE是△ABC的中线
9 .图1是一盏可折叠台灯.图为其平面示意图,底座于点,支架,为固定支撑杆,是的两倍,灯体可绕点旋转调节.现把灯体从水平位置旋转到位置(如图中虚线所示),此时,灯体所在的直线恰好垂直支架,且,则∠的度数为( ).
A. B. C. D.
10 .如图,在△ABC中,∠A=90°,BE,CD分别平分∠ABC和∠ACB,且相交于F,,于点G,则下列结论 ①∠CEG = 2∠DCA;②CA平分∠BCG;③∠ADC =∠GCD;④∠DFB=∠A;⑤∠DFE=135°,其中正确的结论是( )
A.①②③ B.①③④ C.①③④⑤ D.①②③④
填空题(每小题3分,共15分)
11 .已知三角形的两边长分别为和,则第三边的取值范围_____.
12 .如图,在中,,是斜边的中点,将沿直线折叠,点落在点处,如果恰好与垂直,则_______°.
13 .如图,的度数为______度.
14 .如图所示,在正六边形ABCDEF内,以AB为边作正五边形ABGHI,则∠CBG= .
15 .有一张三角形纸片ABC,已知∠B=30°,∠C=50°,点D在边AB上,请在边BC上找一点E,将纸片沿直线DE折叠,点B落在点F处,若EF与三角形纸片ABC的边AC平行,则∠BED的度数为 .
解答题(共8小题,75分)
16 .(10分)(1)求12边形内角和度数;
(2)若一个n边形的内角和与外角和的差是720°,求n.
17 .(7分)如图所示,CD为△ABC的AB边上的中线,△BCD的周长比△ACD的周长大3cm,BC=8cm,求边AC的长.
18.(8分)如图,在中,,的平分线与的外角平分线交于点.
(1)求的度数;
(2)你能说出与之间存在怎样的数量关系吗?
19 .(8分)如图,在中,是高,、是角平分线,它们相交于点,.
(1)的度数为______;
(2)若,求的度数.
20 .(9分)已知:线段AB,CD相交于点O,连接AD,CB,和的平分线AP和CP相交于点P,与CD,AB相交于M,N,如图2:
(1)在图1中,直接写出,,,之间的数量关系;
(2)图中有几个八字模型?
(3)在图2中,与为任意角,试探究与,之间是否存在一定的数量关系,若存在,请写出它们之间的数量关系并证明;若不存在,请说明理由
21 .(8分)【教材呈现】如图是华师版七年级下册数学教材第76页的部分内容如图.
如图,分别用、、表示的三个内角,证明.
延长至点,以点为顶点,在的上侧作,则(同位角相等,两直线平行).
(1)请根据教材提示,结合图①,将证明过程补充完整.
【结论应用】
(2)如图②,在中,,平分,平分,求的度数.
22 .(12分)在和(共边且不重合)中,,.
(1)如图1,当和均为钝角三角形,在直线两侧时,和之间的数量关系为______.
(2)如图2,当和均为锐角三角形,且在直线两侧时,和之间的数量关系为______.
(3)如图3,当为钝角三角形,为锐角三角形,且在直线同侧时,求证:.
(4)分别作和的角平分线,两条角平分线所在直线交于点(点不与点或者点重合),当时,直接写出的度数.
23 .(13分)如图,在△ABC中,点D在AB上,过点D作DE∥BC,交AC于点E,DP平分∠ADE,交∠ACB的平分线于点P,CP与DE相交于点G,∠ACF的平分线CQ与DP相交于点Q.
(1)若∠A=50°,∠B=60°,则∠DPC= °,∠Q ;
(2)若∠A=50°,当∠B的度数发生变化时,∠DPC、∠Q的度数是否发生变化?并说明理由;
(3)若△PCQ中存在一个内角等于另一个内角的三倍,请直接写出所有符合条件的∠A的度数 .
八年级数学上分层优化堂堂清
十一章 三角形
本章综合素质测评(解析版)
时间90分钟满分120分
填空题(每小题3分,共30分)
1.已知三角形两边的长分别是3和7,则此三角形第三边的长可能是( )
A.1 B.2 C.8 D.11
【答案】C.
【解析】根据三角形的三边关系可得7﹣3<x<7+3,再解即可.
设三角形第三边的长为x,由题意得:7﹣3<x<7+3,
4<x<10,故选C
2.如图,工人师傅砌门时,常用木条固定长方形门框,使其不变形,这样做的根据是( )
A.两点之间的线段最短
B.长方形的四个角都是直角
C.长方形是轴对称图形
D.三角形有稳定性
【答案】D
【分析】根据三角形的稳定性,即可求解.
【详解】解:根据题意得:用木条固定长方形门框,使其不变形,这样做的根据是三角形有稳定性.
故选:D
【点评】本题主要考查三角形的稳定性,三角形的稳定性有着稳固、坚定、耐压的特点,因此题中用木条固定门框,使其不变形.
3 .在直角三角形中,有一个锐角为52°,那么另一个锐角的度数( )
A.30° B.48° C.38° D.52°
【答案】C
【分析】根据直角三角形的两个锐角互余即可求得.
【详解】解:由题意可得,
另一个锐角度数为:90°-52°=38°,
故选C.
【点评】本题考查了直角三角形的性质,解决本题的关键是直角三角形的两个锐角互余.
4.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7 B.7或8 C.8或9 D.7或8或9
【答案】D.
【解析】本题考查了多边形的内角和定理,一个多边形截去一个角后它的边数可能增加1,可能减少1,或不变.
首先求得内角和为1080°的多边形的边数,即可确定原多边形的边数.
设内角和为1080°的多边形的边数是n,则(n﹣2) 180°=1080°,
解得:n=8.
则原多边形的边数为7或8或9.
5 .如图,小明在操场上从A点出发,沿直线前进10米后向左转,再沿直线前进10米后,又向左转,这样走下去,他第一次回到出发地A点时,一共走了( )米
A.70 B.80 C.90 D.100
【答案】C
【分析】利用多边形的外角和得出小明回到出发地A点时左转的次数,即可解决问题.
【详解】解:由题意可知,小明第一次回到出发地A点时,他一共转了360°,且每次都是向左转40°,
所以共转了9次,一次沿直线前进10米,9次就前进90米.
故选:C.
【点评】本题考查根据多边形的外角和解决实际问题,注意多边形的外角和是360°.
6 .已知△ABC的三条边分别为a,b,c,化简|a+b﹣c|﹣|b﹣a﹣c|+|a﹣b+c|( )
A.3a﹣b+c B.a+b﹣c C.a﹣b﹣c D.﹣a+3b﹣3c
【答案】B
【分析】根据三角形的任意两边之和大于第三边可得a+b c>0,a b+c>0,b a c<0,再根据绝对值的性质去掉绝对值符号,然后利用整式的加减运算进行计算即可得解.
【详解】解:∵a、b、c分别为△ABC的三边长,
∴a+b c>0,b a c<0,a b+c>0,
∴|a+b c| |b a c|+|a b+c|
=a+b c (a+c b)+a b+c
=a+b c a c+b+a b+c
=a+b c.
故选:B.
7 .如图,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠1+∠2=120°,则∠BA'C的度数为( )
A.120° B.110° C.100° D.90°
解:∵∠BDE、∠CED是△ADE的两个外角,
∴∠BDE=∠A+∠AED,∠CED=∠A+∠ADE,
∴∠BDE+∠CED=∠A+∠AED+∠A+∠ADE,
∴∠1+∠ADE+∠2+∠AED=2∠A+∠AED+∠ADE,
即∠1+∠2=2∠A,
∵∠1+∠2=120°,
∴∠A=60°,
∵BA'平分∠ABC,CA'平分∠ACB,
∴∠A'BC+∠A'CB=(∠ABC+∠ACB)
=(180°﹣∠A)
=90°﹣∠A.
∴∠BA'C=180°﹣(∠A'BC+∠A'CB),
=180°﹣(90°﹣∠A)
=90°+∠A
=90°+×60°
=120°.
故选:A.
8 .如图,D为AC上一点,AD=DC,E为BC上一点,BE=EC,则下列说法不正确的是 ( )
A.DE是△BDC的中线 B.BD是△ABC的中线
C.D是AC的中点,E是BC的中点 D.DE是△ABC的中线
【答案】D
【解析】A.点E是BC的中点,所以DE是△BDC的中线,故A正确,与要求不相符;
B.因为D是△ABC的边AC的中点,所以BD是AC边的中线,故B正确,与要求不相符;
C.由D,E分别是△ABC的边AC,BC的中点可知AD=DC,BE=EC,故C正确,与要求不相符;
D.由三角形的中线的定义可知DE不是△ABC的中线,故D错误,与要求相符.故选D.
9 .图1是一盏可折叠台灯.图为其平面示意图,底座于点,支架,为固定支撑杆,是的两倍,灯体可绕点旋转调节.现把灯体从水平位置旋转到位置(如图中虚线所示),此时,灯体所在的直线恰好垂直支架,且,则∠的度数为( ).
A. B. C. D.
【答案】B
【分析】延长交于点,延长交于点,则,得到,在四边形中,利用四边形的内角和为,列出等式,即可求出的度数.
【详解】解:延长交于点,延长交于点,如图:
,,
,
,,
,
,
,
,
,
,
,
,
在四边形中,有
,
,
解得:;
故选:B.
【点评】本题考查了四边形的内角和的应用,同角的补角相等,邻补角的定义,几何图形中角度的和差关系,解题的关键是正确的作出辅助线,利用四边形的内角和为进行解题.
10 .如图,在△ABC中,∠A=90°,BE,CD分别平分∠ABC和∠ACB,且相交于F,,于点G,则下列结论 ①∠CEG = 2∠DCA;②CA平分∠BCG;③∠ADC =∠GCD;④∠DFB=∠A;⑤∠DFE=135°,其中正确的结论是( )
A.①②③ B.①③④ C.①③④⑤ D.①②③④
【答案】C
【分析】根据平行线的性质与角平分线的定义即可判断①;只需要证明∠ADC+∠ACD=90°,∠GCD+∠BCD=90°,即可判断③;根据角平分线的定义和三角形内角和定理先推出,即可判断④⑤;根据现有条件无法推出②.
【详解】解:∵CD平分∠ACB,
∴∠ACB=2∠DCA,∠ACD=∠BCD
∵,
∴∠CEG=∠ACB=2∠DCA,故①正确;
∵∠A=90°,CG⊥EG,,
∴∠ADC+∠ACD=90°,CG⊥BC,即∠BCG=90°,
∴∠GCD+∠BCD=90°,
又∵∠BCD=∠ACD,
∴∠ADC=∠GDC,故③正确;
∵∠A=90°,
∴∠ABC+∠ACB=90°,
∵BE,CD分别平分∠ABC,∠ACB,
∴,
∴,
∴∠DFB=180°-∠BFC=45°,
∴,故④正确;
∵∠BFC=135°,
∴∠DFE=∠BFC=135°,故⑤正确;
根据现有条件,无法推出CA平分∠BCG,故②错误;
故选C.
【点评】本题主要考查了平行线的性质,角平分线的定义,三角形内角和定理,熟知平行线的性质,角平分线的定义是解题的关键.
填空题(每小题3分,共15分)
11 .已知三角形的两边长分别为和,则第三边的取值范围_____.
【答案】
【分析】设第三边为,根据三角形的三边关系列出不等式即可得到答案.
【详解】解:设第三边为,
已知三角形的两边长分别为和,则第三边的取值范围是,即,
故答案为:.
【点评】本题考查三角形三边关系,熟记三角形三边关系:任意两边之和大于第三边、任意两边之差小于第三边是解决问题的关键.
12 .如图,在中,,是斜边的中点,将沿直线折叠,点落在点处,如果恰好与垂直,则_______°.
【答案】30
【分析】根据折叠的性质可知,折叠前后的两个三角形全等,则 ,从而求得答案.
【详解】解:如图,
在中,,
∵是斜边上的中线,
∴,
∴,
将沿直线折叠,点落在点处,
设度,
∵,
∴,
如果恰好与垂直,
在中,,
即,
解得, ,
∴,
∵,
∴,
即
故答案为:30
【点评】本题考查图形的折叠变化及三角形的内角和定理.关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.
13 .如图,的度数为______度.
【答案】
【分析】如图,交于点,交于点,利用外角的性质,得到:进而得到:,即可得解.
【详解】解:如图,交于点,交于点,
则:,
∴.
故答案为:.
【点评】本题考查三角形外角的性质和三角形的内角和定理.熟练掌握三角形的一个外角等于与它不相邻的两个内角和,以及三角形的内角和定理,是解题的关键.
14 .如图所示,在正六边形ABCDEF内,以AB为边作正五边形ABGHI,则∠CBG= .
解:在正六边形ABCDEF内,正五边形ABGHI中,∠ABC=120°,∠ABG=108°,
∴∠CBG=∠ABC﹣∠ABG=120°﹣108°=12°.
故答案为:12°.
15 .有一张三角形纸片ABC,已知∠B=30°,∠C=50°,点D在边AB上,请在边BC上找一点E,将纸片沿直线DE折叠,点B落在点F处,若EF与三角形纸片ABC的边AC平行,则∠BED的度数为 .
解:①当点F在AB的上方时,如图:
∵AC∥EF,∠C=50°,
∴∠BEF=∠C=50°,
∴∠BED=∠FED=∠BEF=×50°=25°;
②当点F在BC的下方时,如图:
∵AC∥EF,∠C=50°,
∴∠CEF=∠C=50°,
∵∠F=∠B=30°,
∴∠BGD=50°+30°=80°,
∴∠BDG=180°﹣80°﹣30°=70°,
∴∠BDE=∠BDG=×70°=35°;
∴∠BED=180°﹣∠B﹣∠BDE=180°﹣30°﹣35°=115°
综上所述,∠BDE的度数为25°或115°.
故答案为:25°或115°.
解答题(共8小题,75分)
16 .(10分)(1)求12边形内角和度数;
(2)若一个n边形的内角和与外角和的差是720°,求n.
【答案】(1)1800°;(2)8
【分析】(1)根据内角和公式,可得答案;
(2)根据多边形内角和公式(n-2) 180°可得内角和,再根据外角和为360°可得方程(n-2) 180°-360°=720°,再解方程即可.
【详解】解:(1)由题意,得
(12-2)×180°=1800°;
(2)由题意得:
(n-2) 180°-360°=720°,
解得:n=8.
【点睛】此题主要考查了多边形的内角和和外角和,解题的关键是掌握多边形的内角和公式与外角和定理.
17 .(7分)如图所示,CD为△ABC的AB边上的中线,△BCD的周长比△ACD的周长大3cm,BC=8cm,求边AC的长.
【答案】AC的长为5cm.
【解析】根据题意,结合图形,有下列数量关系:①AD=BD,②△BCD的周长比△ACD的周长大3.
依题意:△BCD的周长比△ACD的周长大3cm,
故有:BC+CD+BD-(AC+CD+AD)=3.
又∵ CD为△ABC的AB边上的中线,
∴ AD=BD,即BC-AC=3.
又∵ BC=8,∴ AC=5.
18.(8分)如图,在中,,的平分线与的外角平分线交于点.
(1)求的度数;
(2)你能说出与之间存在怎样的数量关系吗?
【答案】(1)
(2)
【分析】(1)由角平分线的定义可得,,由三角形的外角性质可得:,,再结合,从而可求解;
(2)令,结合(1)的解答过程进行判断即可.
【详解】(1)解:如图所示:
的平分线与的外角平分线交于点,
,,
是的外角,也是的外角,
,,
则有,
是的外角,
,
,
,
即,
得;
(2)当时,
的平分线与的外角平分线交于点,
,,
是的外角,也是的外角,
,,
则有,
是的外角,
,
,
,
即,
.
【点评】本题主要考查三角形的外角性质,角平分线的定义,解答的关键是结合图形,分析清楚各角之间的关系.
19 .(8分)如图,在中,是高,、是角平分线,它们相交于点,.
(1)的度数为______;
(2)若,求的度数.
【答案】(1)
(2)
【分析】(1)根据角平分线的定义得出,根据三角形内角和定理得出,进而即可求解;
(2)根据三角形内角和定理求得,根据是的角平分线,得出,根据 ,即可求解.
【详解】(1)解:∵、是、的角平分线,
∴,
在中,,
∴,
∴,
故答案为:;
(2)解:∵在中,是高,,,
∴,
∵是的角平分线,
∴,
∴ ,
∴.
【点评】本题考查了三角形中线,角平分线,三角形内角和定理,掌握三角形内角和定理是解题的关键.
20 .(9分)已知:线段AB,CD相交于点O,连接AD,CB,和的平分线AP和CP相交于点P,与CD,AB相交于M,N,如图2:
(1)在图1中,直接写出,,,之间的数量关系;
(2)图中有几个八字模型?
(3)在图2中,与为任意角,试探究与,之间是否存在一定的数量关系,若存在,请写出它们之间的数量关系并证明;若不存在,请说明理由
【答案】(1);(2)6个;(3),证明见详解.
【分析】(1)根据三角形内角和定理即可求解;
(2)可以以三角形的公共点为中心寻找;
(3)利用(1)中所得到得结论,列出两组关系式,然后结合角平分线性质即可得证;
【详解】(1) 在和中:
, ,且
(2)一共有6组,分别是:和,和,和,和,和,和;
(3) ,证明如下:
由(1)得:
又 和分别是和的平分线
【点评】本题主要考查了三角形的“8”字模型,充分理解“8”字模型的结论,并利用它进行角度的计算是解决本题的关键.
21 .(8分)【教材呈现】如图是华师版七年级下册数学教材第76页的部分内容如图.
如图,分别用、、表示的三个内角,证明.
延长至点,以点为顶点,在的上侧作,则(同位角相等,两直线平行).
(1)请根据教材提示,结合图①,将证明过程补充完整.
【结论应用】
(2)如图②,在中,,平分,平分,求的度数.
【答案】(1)见详解
(2)
【分析】(1)利用平行线的性质得,即可解答;
(2)利用角平分线的定义和三角形内角和定理可得;
【详解】(1)由题意得:,,
两直线平行,内错角相等,
,
即.
(2),分别平分和,
,,
,
,
,
.
【点评】本题主要考查了平行线的性质,角平分线的定义,三角形内角和定理等知识,熟练掌握平行线的性质,是解题的关键.
22 .(12分)在和(共边且不重合)中,,.
(1)如图1,当和均为钝角三角形,在直线两侧时,和之间的数量关系为______.
(2)如图2,当和均为锐角三角形,且在直线两侧时,和之间的数量关系为______.
(3)如图3,当为钝角三角形,为锐角三角形,且在直线同侧时,求证:.
(4)分别作和的角平分线,两条角平分线所在直线交于点(点不与点或者点重合),当时,直接写出的度数.
【答案】(1)
(2)
(3)见解析
(4)
【分析】(1)根据三角形的外角的性质定理即可求解;
(2)根据多边形的内角和的公式即可求解;
(3)根据三角形的外角和定理,角的等量代换即可求解;
(4)根据题意,结合(1)、(2)、(3)的结论,角平分线的性质,三角形的内角和定理,外角和定理,分类讨论,由此即可求解.
【详解】(1)解:如图所示,延长,
在,中,,,
∵,,,
∴,
∴,
故答案为:.
(2)解:根据四边形的内角和可知,,
∵,,
∴,
∴,
∴,
故答案为:.
(3)证明:如图所示,设交于点,
∵在中,,在中,,
∴,
又∵,,
∴
,
∵,
∴.
(4)解:①如图所示,,分别是的平分线,,
∴,,
∵,,
∴,
∴,
由(1)可知,,
∴,
∴;
②如图所示,,分别是的平分线,,且,,
∴,,
∴,
由(2)可知,,
∴,
在四边形中,根据四边形内角和可得,;
③如图所示,,分别是的平分线,,设交于点,
在中,,在中,,
∴,
∴,
∵,,
∴,
∴,
由(3)可知,,
∴,
∴;
综上所示,的度数为.
【点评】本题主要考查等腰三角形的性质,三角形的内角和定理,外角和定理,四边形的内角和定理,角平分线的性质的综合,掌握以上知识的综合运用是解题的关键.
23 .(13分)如图,在△ABC中,点D在AB上,过点D作DE∥BC,交AC于点E,DP平分∠ADE,交∠ACB的平分线于点P,CP与DE相交于点G,∠ACF的平分线CQ与DP相交于点Q.
(1)若∠A=50°,∠B=60°,则∠DPC= °,∠Q ;
(2)若∠A=50°,当∠B的度数发生变化时,∠DPC、∠Q的度数是否发生变化?并说明理由;
(3)若△PCQ中存在一个内角等于另一个内角的三倍,请直接写出所有符合条件的∠A的度数 .
解:(1)∵∠A=50°,∠B=60°,
∴∠ACB=70°,
∴∠BCP=∠ACB=35°,
∵DE∥BC,
∴∠ADE=∠B=60°,∠PGD=∠PCB=35°,
∵∠PDE=∠ADE=30°,
∴∠DPC=180°﹣∠PDE﹣∠PGD=115°;
又∵∠ACQ=∠ACF,
∴∠PCQ=∠ACQ+∠ACP=(∠ACF+∠ACB)=90°,
∴∠Q=∠DPC﹣∠QCP=25°;
故答案为:115,25;
(2)∠DPC、∠Q的度数不会发生变化.
理由:由(1)得:∵∠PDE=∠ADE=∠B,∠PGD=∠BCP=∠ACB,
∴∠DPC=180°﹣∠PDE﹣∠PGD=180°﹣∠B﹣∠ACB=180°﹣(∠B+∠ACB)=180°﹣(180°﹣∠A)=90°+∠A=115°;
∴∠Q=∠DPC﹣∠QCP=25°;
(3)设∠A=x,则,
∵CP平分∠ACB,CQ平分∠ACF,
∴,,
∴,,
因为△PCQ中存在一个内角等于另一个内角的三倍,
∴①当∠Q=3∠QPC时,,
∴x=135°,
②当∠QPC=3∠Q时,,
∴x=45°,
③当∠PCQ=3∠Q时,,
∴x=60°,
④当∠PCQ=3∠QPC时,,
∴x=120°,
综上①②③④可知∠A=45°或60°或120°或135°.
故答案为:45°或60°或120°或135°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
