3.2.1单调性与最大小值(第1课时) 课件(共24张PPT)
文档属性
| 名称 | 3.2.1单调性与最大小值(第1课时) 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 19:51:29 | ||
图片预览



文档简介
(共24张PPT)
3.2.1 单调性与最大(小)值
第1课时 函数的单调性
3.2 函数的基本性质
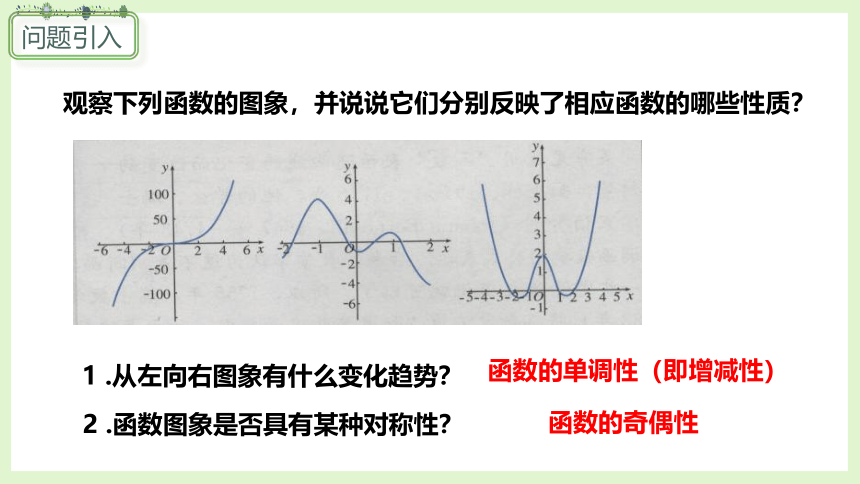
观察下列函数的图象,并说说它们分别反映了相应函数的哪些性质?
1 .从左向右图象有什么变化趋势?
2 .函数图象是否具有某种对称性?
函数的单调性(即增减性)
函数的奇偶性
x
y
o
x
y
o
x
y
o
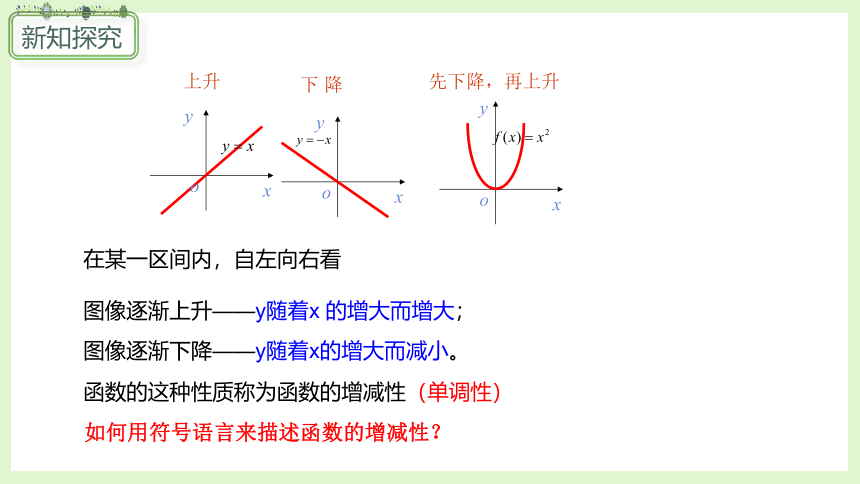
在某一区间内,自左向右看
图像逐渐上升——y随着x 的增大而增大;
图像逐渐下降——y随着x的增大而减小。
函数的这种性质称为函数的增减性(单调性)
先下降,再上升
下 降
上升
如何用符号语言来描述函数的增减性?
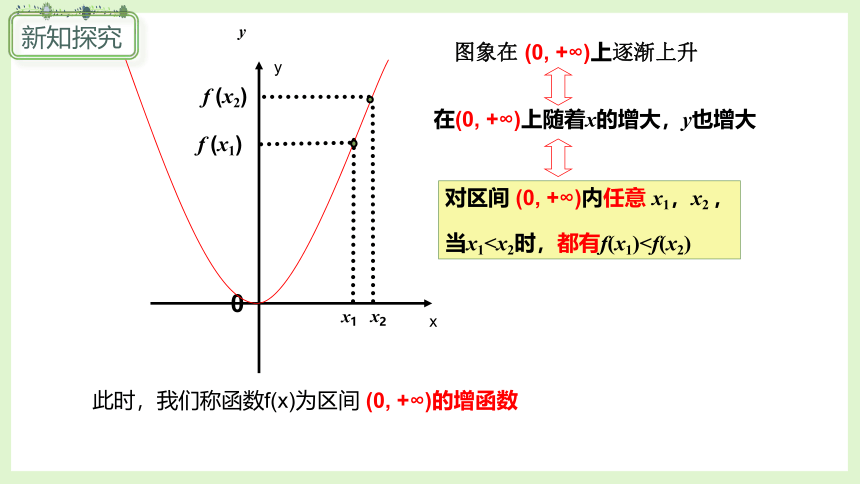
对区间 (0, +∞)内任意 x1,x2 ,
当x1在(0, +∞)上随着x的增大,y也增大
图象在 (0, +∞)上逐渐上升
0
f (x1)
f (x2)
y
x1
x2
x
y
此时,我们称函数f(x)为区间 (0, +∞)的增函数
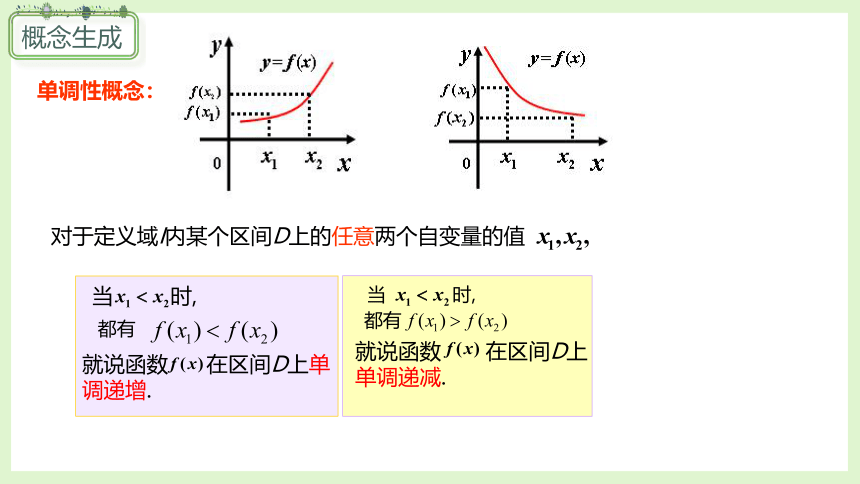
对于定义域I内某个区间D上的任意两个自变量的值
当 时,
都有
就说函数 在区间D上单调递增.
都有
当 时,
就说函数 在区间D上单调递减.
单调性概念:
如果函数 y =f(x)在区间D是增函数或减函数,那么就说函数 y =f(x)在区间D上具有(严格的)单调性,区间D叫做y =f(x)的单调区间。
特别地,
当函数f(x)在它的定义域上单调递增时,我们就称它增函数;
当函数f(x)在它的定义域上单调递减时,我们就称它是减函数;
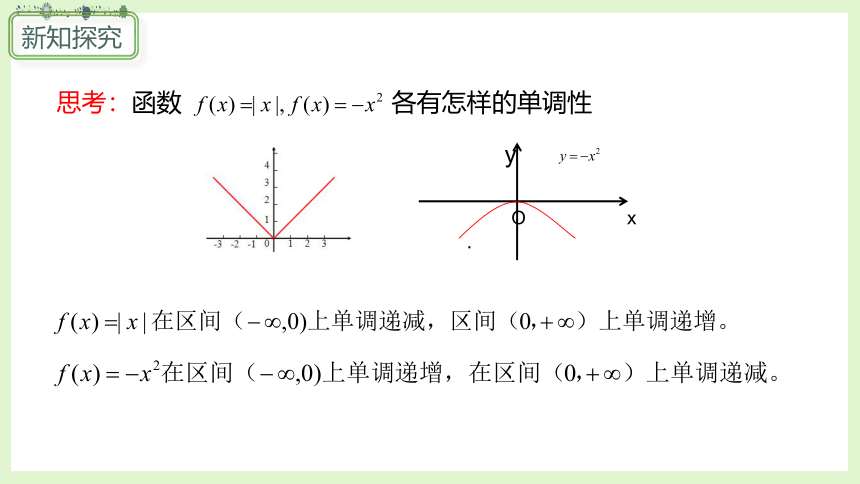
思考:函数 各有怎样的单调性
O
x
y
第一、在中学数学中所说的单调性是指严格的单调性,
即必须是f(x1)f(x2)),而不能是f(x1)≤f(x2) (或f(x1)≥f(x2));
对函数单调性的理解
第二、函数的单调性是对定义域内的某个区间而言的,
是局部概念;
第三、
当x1当x1 f(x2 ) 等价与
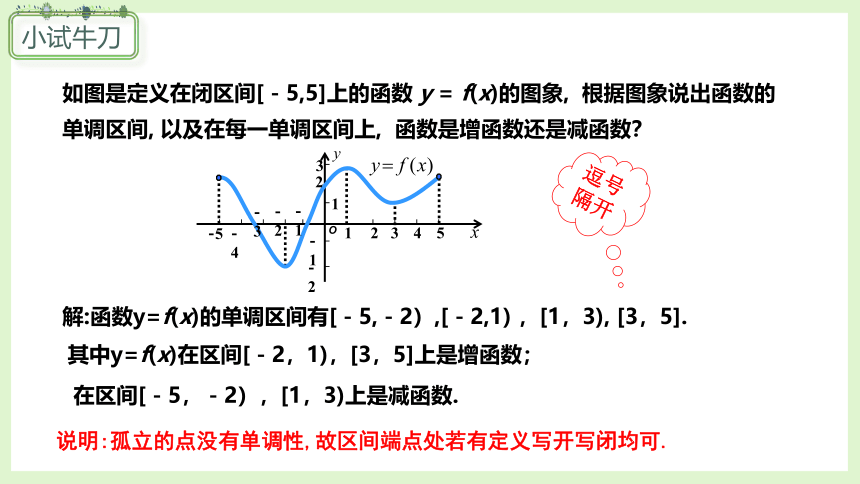
解:函数y=f(x)的单调区间有[-5,-2),[-2,1) ,[1,3), [3,5].
逗号
隔开
如图是定义在闭区间[-5,5]上的函数 y = f(x)的图象, 根据图象说出函数的单调区间, 以及在每一单调区间上, 函数是增函数还是减函数?
其中y=f(x)在区间[-2,1),[3,5]上是增函数;
说明:孤立的点没有单调性,故区间端点处若有定义写开写闭均可.
在区间[-5,-2),[1,3)上是减函数.
-4
3
2
1
5
4
3
1
2
-1
-2
-1
-5
-3
-2
x
y
O
思考1:
思考2:
函数的单调性是对定义域内某个区间而言的,你能举出在整个定义域内是
单调递增的函数例子吗?你能举出在定义域内的某些区间单调递增但在另
一些区间上单调递减的函数例子吗?
1
2
3
4
5
-1
-2
-3
-4
-2
-3
2
3
o
例1:根据定义,研究函数f(x)=2x+3的单调性
思考3:函数f(x)=kx+b(k是怎样的?您能用定义证明你的结论吗?
则
①当k>0时,
于是
②当k<0时,
于是
作差变形
定号
下结论
取值
证明: V1,V2(0,+∞),且V1所以,函数 v∈(0,+∞)是减函数,也就是说,当体积减小时,压强p将增大.
①取值:即设x1、x2是该区间内的任意两个值,且x1②作差变形:即作差f(x1)-f(x2)(或f(x2)-f(x1)),并用因式分解、配方、有理化等方法将差式向有利于判断差的符号的方向变形;
③定号:确定差f(x1)-f(x2)(或f(x2)-f(x1))的符号,当符号不确定时,可进行分类讨论;
④下结论:根据定义得出结论.
利用定义证明或判断函数在指定区间上的单调性的步骤:
提升总结:
例3 根据定义证明函数 在区间 上单调递增。
证明:
所以,函数 在区间 上单调递增。
此函数在(0,1)上的单调性如何?您能证明吗?
对勾函数
1.请根据所给图描述某装配线的生产效率与生产线上工人数量间的关系.
解:在一定范围内,生产效率随着工人数的增加而提高,当工人数达到某个数量时,生产效率达到最大值,而超过这个数量时,生产效率又随着工人数的增加而降低。结论:并不是工人数越多,生产效率越高。
课本79页练习
2.证明函数f(x)=3x+2在R上是减函数.
证明:任取x1,x2∈R且x1则f(x1)-f(x2)=3(x1-x2)<0.
即f(x1)所以,函数f(x)=3x+2在R上是增函数.
4.画出反比例函数f(x)= 的图象.
(1)这个函数的定义域I是什么?
(2)它在定义域I上的单调性是怎样的?
证明你的结论.
同理可证f(x) = 在
1.函数单调性的定义以及函数单调区间的概念;
2.使用定义证明函数的单调性的基本步骤:
(1)取值; (2)作差变形;
(3)定号; (4)下结论.
3.函数的单调性是函数在其定义域上的“局部”性质;
3.2.1 单调性与最大(小)值
第1课时 函数的单调性
3.2 函数的基本性质
观察下列函数的图象,并说说它们分别反映了相应函数的哪些性质?
1 .从左向右图象有什么变化趋势?
2 .函数图象是否具有某种对称性?
函数的单调性(即增减性)
函数的奇偶性
x
y
o
x
y
o
x
y
o
在某一区间内,自左向右看
图像逐渐上升——y随着x 的增大而增大;
图像逐渐下降——y随着x的增大而减小。
函数的这种性质称为函数的增减性(单调性)
先下降,再上升
下 降
上升
如何用符号语言来描述函数的增减性?
对区间 (0, +∞)内任意 x1,x2 ,
当x1
图象在 (0, +∞)上逐渐上升
0
f (x1)
f (x2)
y
x1
x2
x
y
此时,我们称函数f(x)为区间 (0, +∞)的增函数
对于定义域I内某个区间D上的任意两个自变量的值
当 时,
都有
就说函数 在区间D上单调递增.
都有
当 时,
就说函数 在区间D上单调递减.
单调性概念:
如果函数 y =f(x)在区间D是增函数或减函数,那么就说函数 y =f(x)在区间D上具有(严格的)单调性,区间D叫做y =f(x)的单调区间。
特别地,
当函数f(x)在它的定义域上单调递增时,我们就称它增函数;
当函数f(x)在它的定义域上单调递减时,我们就称它是减函数;
思考:函数 各有怎样的单调性
O
x
y
第一、在中学数学中所说的单调性是指严格的单调性,
即必须是f(x1)
对函数单调性的理解
第二、函数的单调性是对定义域内的某个区间而言的,
是局部概念;
第三、
当x1
解:函数y=f(x)的单调区间有[-5,-2),[-2,1) ,[1,3), [3,5].
逗号
隔开
如图是定义在闭区间[-5,5]上的函数 y = f(x)的图象, 根据图象说出函数的单调区间, 以及在每一单调区间上, 函数是增函数还是减函数?
其中y=f(x)在区间[-2,1),[3,5]上是增函数;
说明:孤立的点没有单调性,故区间端点处若有定义写开写闭均可.
在区间[-5,-2),[1,3)上是减函数.
-4
3
2
1
5
4
3
1
2
-1
-2
-1
-5
-3
-2
x
y
O
思考1:
思考2:
函数的单调性是对定义域内某个区间而言的,你能举出在整个定义域内是
单调递增的函数例子吗?你能举出在定义域内的某些区间单调递增但在另
一些区间上单调递减的函数例子吗?
1
2
3
4
5
-1
-2
-3
-4
-2
-3
2
3
o
例1:根据定义,研究函数f(x)=2x+3的单调性
思考3:函数f(x)=kx+b(k是怎样的?您能用定义证明你的结论吗?
则
①当k>0时,
于是
②当k<0时,
于是
作差变形
定号
下结论
取值
证明: V1,V2(0,+∞),且V1
①取值:即设x1、x2是该区间内的任意两个值,且x1
③定号:确定差f(x1)-f(x2)(或f(x2)-f(x1))的符号,当符号不确定时,可进行分类讨论;
④下结论:根据定义得出结论.
利用定义证明或判断函数在指定区间上的单调性的步骤:
提升总结:
例3 根据定义证明函数 在区间 上单调递增。
证明:
所以,函数 在区间 上单调递增。
此函数在(0,1)上的单调性如何?您能证明吗?
对勾函数
1.请根据所给图描述某装配线的生产效率与生产线上工人数量间的关系.
解:在一定范围内,生产效率随着工人数的增加而提高,当工人数达到某个数量时,生产效率达到最大值,而超过这个数量时,生产效率又随着工人数的增加而降低。结论:并不是工人数越多,生产效率越高。
课本79页练习
2.证明函数f(x)=3x+2在R上是减函数.
证明:任取x1,x2∈R且x1
即f(x1)
4.画出反比例函数f(x)= 的图象.
(1)这个函数的定义域I是什么?
(2)它在定义域I上的单调性是怎样的?
证明你的结论.
同理可证f(x) = 在
1.函数单调性的定义以及函数单调区间的概念;
2.使用定义证明函数的单调性的基本步骤:
(1)取值; (2)作差变形;
(3)定号; (4)下结论.
3.函数的单调性是函数在其定义域上的“局部”性质;
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
