九年级数学上分层优化堂堂清(9)22.3 实际问题与二次函数——面积问题(含解析)
文档属性
| 名称 | 九年级数学上分层优化堂堂清(9)22.3 实际问题与二次函数——面积问题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
九年级数学上分层优化堂堂清
二十二章 二次函数
22.3实际问题与二次函数
第一课时 面积问题
学习目标:
1 会求二次函数y=ax2+bx+c的最小(大)值.
2 能够从实际问题中抽象出二次函数关系,并运用二次函数及性质解决最小(大)值等实际问题.
一、利用二次函数解决实际问题的步骤:
1.分析题意,把实际问题转化为数学问题,画出图形.
2.根据已知条件建立适当的平面直角坐标系.
3.选用适当的函数解析式求解.
4.根据二次函数的解析式解决具体的实际问题.
二、利用二次函数解决面积最值的方法:
①找好自变量;
②利用相关的图象面积公式,列出函数关系式;
③利用函数的最值解决面积最值问题。
【注意】自变量的取决范围。
基础提升 教材核心知识点精练
知识点1:求二次函数的最大(最小值)
【例1-1】 已知点在二次函数的图象上,则的最小值为( )
A.-8 B.8 C.-9 D.9
【例1-1】 当时,二次函数的最小值为8,则a的值为( )
A.或5 B.0或6 C.或6 D.0或5
.
知识点2: 图形面积的最值问题
【例2-1】 如图,利用一面长18米的墙,用篱笆围成一个矩形场地,设长为x米,长为y米,且.
(1)若篱笆的长为36米,求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)在(1)的条件下,求出使矩形场地的面积为160平方米的围法.
【例2-2】某家禽养殖场,用总长为200m的围栏靠墙(墙长为65m)围成如图所示的三块矩形区域,矩形EAGH与矩形HGBF面积相等,矩形EAGH面积等于矩形DEFC面积的二分之一,设AD长为xm,矩形区域ABCD的面积为ym2.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,y有最大值?最大值是多少?
(3)现需要在矩形EAGH和矩形DEFC区域分别安装不同种类的养殖设备,单价分别为40元/平方米和20元/平方米,若要使安装成本不超过30000元,请直接写出x的取值范围.
能力强化 能力强化训练
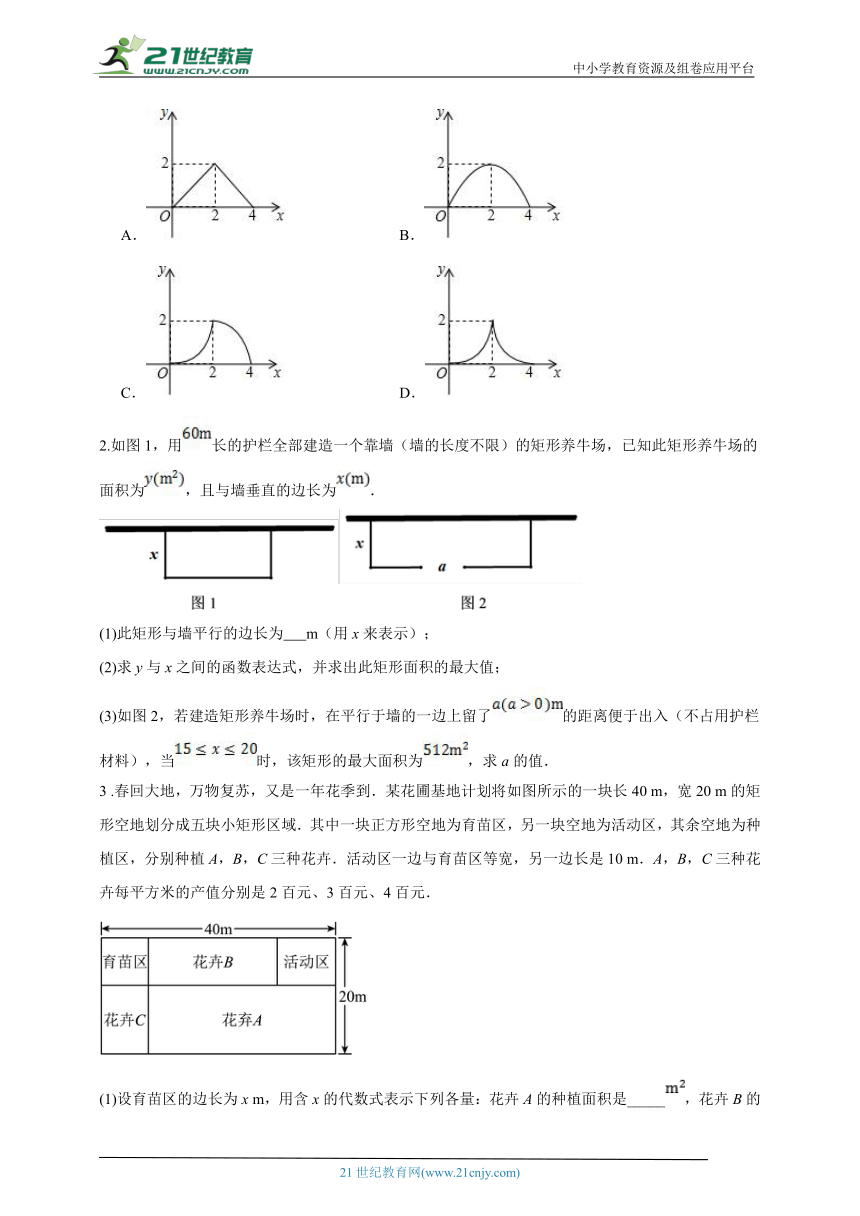
1.如图,在等腰Rt△ABC中,∠C=90°,直角边AC长与正方形MNPQ的边长均为2cm,CA与MN在直线l上.开始时A点与M点重合;让△ABC向右平移;直到C点与N点重合时为止.设△ABC与正方形MNPQ重叠部分(图中阴影部分)的面积为ycm2,MA的长度为xcm,则y与x之间的函数关系大致是( )
A. B.
C. D.
2.如图1,用长的护栏全部建造一个靠墙(墙的长度不限)的矩形养牛场,已知此矩形养牛场的面积为,且与墙垂直的边长为.
(1)此矩形与墙平行的边长为 m(用x来表示);
(2)求y与x之间的函数表达式,并求出此矩形面积的最大值;
(3)如图2,若建造矩形养牛场时,在平行于墙的一边上留了的距离便于出入(不占用护栏材料),当时,该矩形的最大面积为,求a的值.
3 .春回大地,万物复苏,又是一年花季到.某花圃基地计划将如图所示的一块长40 m,宽20 m的矩形空地划分成五块小矩形区域.其中一块正方形空地为育苗区,另一块空地为活动区,其余空地为种植区,分别种植A,B,C三种花卉.活动区一边与育苗区等宽,另一边长是10 m.A,B,C三种花卉每平方米的产值分别是2百元、3百元、4百元.
(1)设育苗区的边长为x m,用含x的代数式表示下列各量:花卉A的种植面积是_____,花卉B的种植面积是______,花卉C的种植面积是_______.
(2)育苗区的边长为多少时,A,B两种花卉的总产值相等?
(3)若花卉A与B的种植面积之和不超过 ,求A,B,C三种花卉的总产值之和的最大值.
堂堂清
一、选择题(每小题4分,共32分)
1.利用长为的墙和长的篱笆来围成一个矩形苗圃园,若平行于墙的一边长不小于,则这个苗圃园面积的最大值和最小值分别为( )
A., B., C., D.,
2.九年级某班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形、等腰直角三角形(底边靠墙)、半圆形这三种方案,如图所示,最佳方案是( )
A.方案1 B.方案2 C.方案3 D.面积都一样
3.如图,要围一个矩形菜园,共中一边是墙,且的长不能超过,其余的三边用篱笆,且这三边的和为.有下列结论:
①的长可以为;
②的长有两个不同的值满足菜园面积为;
③菜园面积的最大值为.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
4.如图1所示的矩形窗框的周长及其两条隔断、的总长为米,且隔断、分别与矩形的两条邻边平行,设的长为米,矩形的面积为平方米,关于的函数图像如图2,则下列说法正确的是( )
A.矩形的最大面积为8平方米 B.与之间的函数关系式为
C.当时,矩形的面积最大 D.的值为12
5.如图1,一张边长为、的长方形纸片的面积等于,将它通过割、拼,再补一个正方形,拼成一个新的正方形(如图2),可以取得的最小整数是( )
A. B. C. D.3
6.如图,四边形中,,若,则四边形的面积最大值是( )
A.4 B.6 C.8 D.10
7.如图,晓波家的院墙一边靠墙处,用米长的铁栅栏围成了三个相连的养殖小院子,总面积为平方米,为方便喂养这些不同类的动物,在各个养殖院子之间留出了米宽的缺口作通道,在平行于墙的一边留下一个米宽的缺口作小门.若设米,则关于的函数关系式为( )
A. B.
C. D.
8.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的两处各留宽的门.已知计划中的材料可建墙体(不包括门)总长为,则当能建成的饲养室总占地面积最大时,中间隔开的墙长是( )米.
A.4 B.5 C.6 D.8
二、填空题(每小题4分,共20分)
9.如图,王叔叔想用长为的栅栏,再借助房屋的外墙围成一个矩形羊圈,已知房屋外墙足够长,当矩形的边 时,羊圈的面积最大.
10.如图,P是抛物线在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形周长的最大值为 .
11.长方形的周长为,其中一边长为(其中),面积为,则与的关系式为 .
12.如图,某活动板房由矩形和抛物线构成,矩形的边长,,抛物线的最高点E到BC的距离为.在该抛物线与之间的区域内装有一扇矩形窗户,点G、H在边上,点F、K在该抛物线上.按如图所示建立平面直角坐标系.若,则矩形窗户的宽的长为 m.
13.如图,有一矩形纸片,长、宽分别为厘米和厘米,现在长宽上分别剪去宽为厘米()的纸条,则剩余部分(图中阴影部分)的面积关于的函数关系式为 .
三、解答题(共48分)
14.如图,要利用一面墙(长为)建羊圈,用100m长的围栏围成两个大小相同的矩形羊圈,每个羊圈留有个宽的门(留门部分不需要围栏),若宽用x(m)表示,总面积用y()表示.
(1)写出总面积y()关于宽x(m)的函数关系式:
(2)当面积时,求羊圈的宽x的值.
15.工匠师傅准备从六边形的铁皮中,裁出一块矩形铁皮制作工件,如图所示.经测量,,与之间的距离为2米,米,米,,.,,是工匠师傅画出的裁剪虚线.当的长度为多少时,矩形铁皮的面积最大,最大面积是多少?
16.为响应广州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边露墙,可利用的墙长不超过,另外三边由长的栅栏围成,设矩形空地中,垂直于墙的边,面积为(如图).
(1)求与之间的函数关系式,并写出自变量的取值范围;
(2)若矩形空地的面积为,求的值;
(3)为何值时,有最大值?最大值是多少?
17.2023年南宁市公共资源交易中心明确提出将五象站铁路枢纽接入地铁4号线.目前4号线剩余的东段(五象火车站-龙岗站)已经在建设中,施工方决定对终点站龙岗站施工区域中的一条特殊路段进行围挡施工,先沿着路边砌了一堵长的砖墙,然后打算用长的铁皮围栏靠着墙围成中间隔有一道铁皮围栏(平行于)的长方形施工区域.
(1)设施工区域的一边为,施工区域的面积为.请求出S与x的函数关系式,并直接写出自变量x的取值范围;
(2)当围成的施工区域面积为时,的长是多少?
(3)该特殊路段围挡区域的施工成本为400元/,项目方打算拨款120000元用于施工,请你通过计算判断项目方的拨款能否够用.
18.某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为),另外三面用栅栏围成,中间再用栅栏把它分成两个面积为的矩形,已知栅栏的总长度为.
(1)若矩形养殖场的总面积为36,求长度;
(2)求矩形养殖场的总面积最大值为多少.
19.如图,抛物线与轴交于、,交轴于.
(1)求抛物线的表达式;
(2)是直线上方的抛物线上的一个动点,设的横坐标为,当四边形的面积最大时,求出面积的最大值及点的坐标;
(3)设点是轴上的动点,在平面直角坐标系中,存在点,使得以点为顶点的四边形是菱形,直接写出所有符合条件的点坐标.
九年级数学上分层优化堂堂清
二十二章 二次函数
22.3实际问题与二次函数
第一课时 面积问题 (解析版)
学习目标:
1 会求二次函数y=ax2+bx+c的最小(大)值.
2 能够从实际问题中抽象出二次函数关系,并运用二次函数及性质解决最小(大)值等实际问题.
一、利用二次函数解决实际问题的步骤:
1.分析题意,把实际问题转化为数学问题,画出图形.
2.根据已知条件建立适当的平面直角坐标系.
3.选用适当的函数解析式求解.
4.根据二次函数的解析式解决具体的实际问题.
二、利用二次函数解决面积最值的方法:
①找好自变量;
②利用相关的图象面积公式,列出函数关系式;
③利用函数的最值解决面积最值问题。
【注意】自变量的取决范围。
基础提升 教材核心知识点精练
知识点1:求二次函数的最大(最小值
【例1-1】 已知点在二次函数的图象上,则的最小值为( )
A.-8 B.8 C.-9 D.9
【答案】C
【分析】根据点在函数图象上可得,继而可得,由二次函数的最值即可得出答案.
【详解】解:依题意得:,
∴
∴当时,有最小值为,
故选:C.
【点评】本题主要考查了函数图象上点的特征,正确得出是解题关键.
【例1-1】 当时,二次函数的最小值为8,则a的值为( )
A.或5 B.0或6 C.或6 D.0或5
【答案】C
【分析】由,可知二次函数对称轴为直线,且图象开口向上,当时,,计算求出满足要求的值即可;当,即时,,计算求出满足要求的值即可.
【详解】解:,
∴二次函数对称轴为直线,且图象开口向上,
∴当时,,解得,或(舍去),
当,即时,,解得,或(舍去),
综上,a的值为或6,
故选:C.
【点评】本题考查了二次函数的图象与性质,二次函数的最值.解题的关键在于对知识的熟练掌握与灵活运用.
知识点2: 图形面积的最值问题
【例2-1】 如图,利用一面长18米的墙,用篱笆围成一个矩形场地,设长为x米,长为y米,且.
(1)若篱笆的长为36米,求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)在(1)的条件下,求出使矩形场地的面积为160平方米的围法.
【答案】(1),
(2)长为16米,长为10米
【分析】(1)由图可知篱笆长,把相关数值代入即可求解;
(2)列出矩形面积S与x的关系式,再令,求出方程的解,可得结果.
【详解】(1)解:,
,
.
,,
,
,
又,
,
.
(2)设矩形的面积为,
则,
当时得:
,解得:,,
,
,
,,
答:当长为16米,长为10米时,矩形的面积为160平方米.
【点评】此题考查了二次函数的应用,不仅是一道实际问题,而且结合了矩形的性质,解答此题要注意以下问题:(1)矩形的一边为墙,且墙的长度不超过18米;(2)根据矩形的面积公式列一元二次方程并根据根的判别式来判断是否两边长相等.
【例2-2】某家禽养殖场,用总长为200m的围栏靠墙(墙长为65m)围成如图所示的三块矩形区域,矩形EAGH与矩形HGBF面积相等,矩形EAGH面积等于矩形DEFC面积的二分之一,设AD长为xm,矩形区域ABCD的面积为ym2.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,y有最大值?最大值是多少?
(3)现需要在矩形EAGH和矩形DEFC区域分别安装不同种类的养殖设备,单价分别为40元/平方米和20元/平方米,若要使安装成本不超过30000元,请直接写出x的取值范围.
【解答】解:(1)由题意得,AE=HG=AD=xm,
DC=AB=(200﹣x)=(100﹣x)m,
故y=x(100﹣x)=﹣x2+100x,
自变量x的取值范围为:28≤x<80;
(2)由题意可得:
∵y=﹣x2+100x=﹣( x2﹣80x)=﹣( x﹣40)2+2000,
又∵28≤x<80,
∴当x=40时,y有最大值,最大值为2000平方米;
(3)由题意得,S矩形EAGH=AG AE=(100﹣x)x=﹣x2+25x,S矩形DEFC=DC DE=(100﹣x) x=﹣x2+50x,
设安装成本为w元,则w=40(﹣x2+25x)+20(﹣x2+50x)=﹣25x2+2000x,
令w=30000,则﹣25x2+2000x=30000,
解得x=60或20,
∵28≤x<80,
∴60≤x<80时,安装成本不超过30000元.
能力强化 能力强化训练
1.如图,在等腰Rt△ABC中,∠C=90°,直角边AC长与正方形MNPQ的边长均为2cm,CA与MN在直线l上.开始时A点与M点重合;让△ABC向右平移;直到C点与N点重合时为止.设△ABC与正方形MNPQ重叠部分(图中阴影部分)的面积为ycm2,MA的长度为xcm,则y与x之间的函数关系大致是( )
A. B.
C. D.
【答案】C
【分析】根据动点的运动过程确定每段阴影部分与x的关系类型,根据函数的性质确定选项.
【详解】解:当x≤2cm时,重合部分是边长为x的等腰直角三角形,
面积为:y=x2,
是一个开口向上的二次函数;
当x>2时,
重合部分是直角梯形,
面积为:y=8﹣(x﹣2)2,
是一个开口向下的二次函数,
故选:C.
【点评】本题是对函数图像的考查,熟练掌握图像的面积及函数知识是解决本题的关键.
2.如图1,用长的护栏全部建造一个靠墙(墙的长度不限)的矩形养牛场,已知此矩形养牛场的面积为,且与墙垂直的边长为.
(1)此矩形与墙平行的边长为 m(用x来表示);
(2)求y与x之间的函数表达式,并求出此矩形面积的最大值;
(3)如图2,若建造矩形养牛场时,在平行于墙的一边上留了的距离便于出入(不占用护栏材料),当时,该矩形的最大面积为,求a的值.
【答案】(1)
(2)450
(3)4
【分析】(1)将长的护栏减去即可;
(2)根据矩形的面积定义长乘以宽,即可求出y与x之间的函数表达式,由二次函数的顶点坐标即可求出矩形面积的最大值;
(3)先求出y与x之间的函数表达式,再求出,由矩形的最大面积为,得,解出a的值,舍去负数,即可得答案.
【详解】(1)解:由题意得:此矩形与墙平行的边长为;
故答案为:
(2),
y与x之间的函数表达式是,矩形面积的最大值450;
(3),
二次函数的对称轴,
,
,
,
矩形的最大面积为,
,
解得:或(舍去),
.
【点评】本题考查了二次函数在实际问题中的应用,根据题意正确得出函数关系式并明确二次函数的性质是解题的关键.
3 .春回大地,万物复苏,又是一年花季到.某花圃基地计划将如图所示的一块长40 m,宽20 m的矩形空地划分成五块小矩形区域.其中一块正方形空地为育苗区,另一块空地为活动区,其余空地为种植区,分别种植A,B,C三种花卉.活动区一边与育苗区等宽,另一边长是10 m.A,B,C三种花卉每平方米的产值分别是2百元、3百元、4百元.
(1)设育苗区的边长为x m,用含x的代数式表示下列各量:花卉A的种植面积是_____,花卉B的种植面积是______,花卉C的种植面积是_______.
(2)育苗区的边长为多少时,A,B两种花卉的总产值相等?
(3)若花卉A与B的种植面积之和不超过 ,求A,B,C三种花卉的总产值之和的最大值.
【答案】(1);;
(2)32m或10m
(3)168000元
【分析】(1)根据正方形和长方形的面积计算公式可直接得到答案;
(2)根据A,B两种花卉的总产值相等建立一元二次方程,解方程即可得到答案;
(3)先根据花卉A与B的种植面积之和不超过建立不等式,得到,再设A,B,C三种花卉的总产值之和y百元,得到y关于x的二次函数,根据二次函数的图形性质即可得到答案.
【详解】(1)解:∵育苗区的边长为x m,活动区的边长为10m,
∴花卉A的面积为: ,
花卉B的面积为: ,
花卉C的面积为: ,
故答案为:;;;
(2)解:∵A,B花卉每平方米的产值分别是2百元、3百元,
∴A,B两种花卉的总产值分别为百元和百元,
∵A,B两种花卉的总产值相等,
∴,
∴,
解方程得或,
∴当育苗区的边长为32m或10m时,A,B两种花卉的总产值相等;
(3)解:∵花卉A与B的种植面积之和为: ,
∴,
∴,
∵设A,B,C三种花卉的总产值之和y百元,
∴,
∴,
∴,
∴当时,y随x的增加而减小,
∴当时,y最大,且(百元),
故A,B,C三种花卉的总产值之和的最大值168000元.
【点评】本题考查一元二次方程和二次函数的应用,解题的关键是根据题意建立正确的方程和函数表达式.
堂堂清
一、选择题(每小题4分,共32分)
利用长为的墙和长的篱笆来围成一个矩形苗圃园,若平行于墙的一边长不小于,则这个苗圃园面积的最大值和最小值分别为( )
A., B., C., D.,
【答案】.A
【分析】设垂直于墙的一边长为,则平行于墙的一边长为,矩形面积为,先根据平行于墙的长度不小于,墙的长度为求出,再根据矩形面积公式求出,由此利用二次函数的性质求解即可.
【详解】解;设垂直于墙的一边长为,则平行于墙的一边长为,矩形面积为,
∵平行于墙的一边长不小于,墙的长度为
∴,
∴,
,
∵,
∴当时,y随x增大而减小,
∴当时,,
当时,,
∴这个苗圃园面积的最大值和最小值分别为,,
故选A.
【点评】本题主要考查了二次函数的实际应用,一元一次不等式组的实际应用,正确求出矩形面积与垂直于墙的一边的二次函数关系式是解题的关键.
2.九年级某班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形、等腰直角三角形(底边靠墙)、半圆形这三种方案,如图所示,最佳方案是( )
A.方案1 B.方案2 C.方案3 D.面积都一样
【答案】C
【分析】根据二次函数的性质,分别计算出三个方案的菜园面积进行比较即可.
【详解】解:方案1:设米,则米,
则菜园面积,
当时,此时菜园最大面积为8平方米;
方案2:如图,,
∵,
∴菜园面积为8平方米;
方案3:半圆的半径为米,
∴此时菜园最大面积(平方米)
∵,
∴方案3的菜园面积最大,
∴在三种方案中,最佳方案是方案3.
故选:C.
【点评】本题考查了二次函数的应用、圆的面积、等腰三角形的性质,根据题意计算三个方案的边长及半径是解本题的关键.
3.如图,要围一个矩形菜园,共中一边是墙,且的长不能超过,其余的三边用篱笆,且这三边的和为.有下列结论:
①的长可以为;
②的长有两个不同的值满足菜园面积为;
③菜园面积的最大值为.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
【答案】C
【分析】设的长为,矩形的面积为,则的长为,根据矩形的面积公式列二次函数解析式,再分别根据的长不能超过,二次函数的最值,解一元二次方程求解即可.
【详解】设的长为,矩形的面积为,则的长为,由题意得
,
其中,即,
①的长不可以为,原说法错误;
③菜园面积的最大值为,原说法正确;
②当时,解得或,
∴的长有两个不同的值满足菜园面积为,说法正确;
综上,正确结论的个数是2个,
故选:C.
【点评】本题考查了二次函数的应用,解一元二次方程,准确理解题意,列出二次函数解析式是解题的关键.
4.如图1所示的矩形窗框的周长及其两条隔断、的总长为米,且隔断、分别与矩形的两条邻边平行,设的长为米,矩形的面积为平方米,关于的函数图像如图2,则下列说法正确的是( )
A.矩形的最大面积为8平方米 B.与之间的函数关系式为
C.当时,矩形的面积最大 D.的值为12
【答案】D
【分析】观察图2,得出当时,函数值最大,根据题意确定a的值,并可求出二次函数解析式,即可做出正确判断.
【详解】解:由图2可知,函数图像最高点为,经过原点,
设二次函数解析式为,
代入,解得,
由此判断:A.矩形最大面积是4平方米,选项错误;
B.二次函数解析式为,选项错误;
C.矩形面积最大时,,选项错误;
D.当时,矩形面积取最大值,,,选项正确.
故选:D.
【点评】本题考查二次函数图像和性质,解题的关键是识别函数图像,确定自变量的取值为何值时函数取得最大值,并利用待定系数法求得函数解析式.
5.如图1,一张边长为、的长方形纸片的面积等于,将它通过割、拼,再补一个正方形,拼成一个新的正方形(如图2),可以取得的最小整数是( )
A. B. C. D.3
【答案】B
【分析】利用长方形的面积公式,可得出关于的函数关系式,再利用二次函数的性质,即可解决最值问题.
【详解】解:根据题意得:,
,
.
,且,
当时,随的增大而增大,
当时,可以取得最小整数,此时.
故选:B.
【点评】本题考查了二次函数的性质以及二次函数的最值,根据各数量之间的关系,找出k关于a的函数关系式是解题的关键.
6.如图,四边形中,,若,则四边形的面积最大值是( )
A.4 B.6 C.8 D.10
【答案】C
【分析】设,,根据题意表示四边形的面积,根据二次函数的性质作答即可.
【详解】解:如图,设、交于点M,
设,
,
,
由题意,得:四边形的面积为,
即四边形的面积,
∴当时,四边形的面积最大,最大为8.
故选:C.
【点评】本题考查了二次函数与几何的综合应用.根据题意,将四边形的面积问题转化为二次函数求最值问题,是解题的关键.
7.如图,晓波家的院墙一边靠墙处,用米长的铁栅栏围成了三个相连的养殖小院子,总面积为平方米,为方便喂养这些不同类的动物,在各个养殖院子之间留出了米宽的缺口作通道,在平行于墙的一边留下一个米宽的缺口作小门.若设米,则关于的函数关系式为( )
A. B.
C. D.
【答案】D
【分析】如图所示(见详解),设米,则可求出的长,根据矩形的面积公式即可求解.
【详解】解:如图所示,
设米,则,
又小院子的总面积为,
∴,
故选:.
【点评】本题主要考查二次函数的运用,理解图形面积的计算方法,掌握数量关系,准确列出函数关系式是解题的关键.
8.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的两处各留宽的门.已知计划中的材料可建墙体(不包括门)总长为,则当能建成的饲养室总占地面积最大时,中间隔开的墙长是( )米.
A.4 B.5 C.6 D.8
【答案】B
【分析】根据题意,设能建成的饲养室总占地的面积为,根据二次函数的性质即可求解.
【详解】解:设中间隔开的墙长为,能建成的饲养室总占地的面积为,
根据题意得,,,有最大值,
∴当时,取得最大值,
故选:B.
【点评】本题考查了二次函数的应用,根据题意列出函数关系式是解题的关键.
二、填空题(每小题4分,共20分
9.如图,王叔叔想用长为的栅栏,再借助房屋的外墙围成一个矩形羊圈,已知房屋外墙足够长,当矩形的边 时,羊圈的面积最大.
【答案】15
【分析】设为,则,根据矩形的面积公式可得关于x的二次函数关系式,配方后即可解.
【详解】解:设为,面积为,
由题意可得:,
当时,取得最大值,
即时,羊圈的面积最大,
故答案为:.
【点评】本题考查了二次函数的性质在实际生活中的应用.最大面积的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.其中要注意应该在自变量的取值范围内求最大值(或最小值),也就是说二次函数的最值不一定在时取得.
10.如图,P是抛物线在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形周长的最大值为 .
【答案】/12.5
【分析】设点P的坐标为,,根据四边形的周长得到:,再由二次函数的性质即可求得最大值.
【详解】解:设点P的坐标为,,
由题意可知:四边形的周长,
∴,
当时,C有最大值.
故答案为:.
【点评】本题考查了二次函数的最值及二次函数的图像上点的坐标特征,最后根据二次函数的性质求最值是解题的关键.
11.长方形的周长为,其中一边长为(其中),面积为,则与的关系式为 .
【答案】
【分析】首先利长方形周长公式表示出长方形的另一边长,然后利用长方形的面积公式求解.
【详解】解:∵长方形的周长为,长方形的一边长为,
∴另一边长为,
则与的关系式为,
故答案为:.
【点评】本题考查了列函数关系式,理解长方形的边长、周长以及面积之间的关系是关键.
12.如图,某活动板房由矩形和抛物线构成,矩形的边长,,抛物线的最高点E到BC的距离为.在该抛物线与之间的区域内装有一扇矩形窗户,点G、H在边上,点F、K在该抛物线上.按如图所示建立平面直角坐标系.若,则矩形窗户的宽的长为 m.
【答案】/
【分析】利用待定系数法求出抛物线解析式,设,求出,即可得到矩形窗户的宽的长.
【详解】解:由题意可知,、、,
设抛物线解析式为,
,解得:
抛物线解析式为,
点G、H在边上,且,
、,
四边形是矩形,
设,
点在抛物线上,
,
,
故答案为:.
【点评】本题考查了坐标与图形,待定系数法求函数解析式,矩形的性质,二次函数的性质等知识,求出二次函数解析式,掌握二次函数的性质是解题关键.
13.如图,有一矩形纸片,长、宽分别为厘米和厘米,现在长宽上分别剪去宽为厘米()的纸条,则剩余部分(图中阴影部分)的面积关于的函数关系式为 .
【答案】
【分析】阴影部分的长方形的的长为,宽为,然后根据长方形的面积公式即可求解.
【详解】阴影部分的长方形的的长为,宽为,
所以面积.
【点评】本题考查了利用长方形的面积公式列出函数关系式,其中根据题意,找到所求量的等量关系是解决问题的关键.
三、解答题(共48分)
14.(8分)如图,要利用一面墙(长为)建羊圈,用100m长的围栏围成两个大小相同的矩形羊圈,每个羊圈留有个宽的门(留门部分不需要围栏),若宽用x(m)表示,总面积用y()表示.
(1)写出总面积y()关于宽x(m)的函数关系式:
(2)当面积时,求羊圈的宽x的值.
【答案】(1)
(2)羊圈的宽x的值为26米
【分析】(1)根据长方形面积公式求解即可;
(2)把代入(1)中的解析式,解一元二次方程求解即可.
【详解】(1)由题意得,,
∵,
∴,
∵,
∴,
∴;
(2)当时,
解得(不合题意,舍去),
∴羊圈的宽x的值为26米.
【点评】本题考查了二次函数的应用和解一元二次方程,准确理解题意,熟练掌握解方程的方法是解题的关键.
15.(7分)工匠师傅准备从六边形的铁皮中,裁出一块矩形铁皮制作工件,如图所示.经测量,,与之间的距离为2米,米,米,,.,,是工匠师傅画出的裁剪虚线.当的长度为多少时,矩形铁皮的面积最大,最大面积是多少?
【答案】当的长度为米时,矩形铁皮的面积最大,最大面积是平方米
【分析】连接,分别交于点,交于点,先判断出四边形是矩形,从而可得,再判断出四边形和四边形都是矩形,从而可得米,,然后设矩形的面积为平方米,米,则米,米,利用矩形的面积公式可得关于的二次函数,最后利用二次函数的性质求解即可得.
【详解】解:如图,连接,分别交于点,交于点,
,
,
米,
四边形是平行四边形,
又,
四边形是矩形,
,,
,
,
四边形是矩形,
,
四边形和四边形都是矩形,
米,,
和都是等腰直角三角形,
,
,
设矩形的面积为平方米,米,则米,米,
米,
米,
,
又,与之间的距离为2米,米,
,
由二次函数的性质可知,当时,随的增大而增大;当时,随的增大而减小,
则当时,取得最大值,最大值为,
答:当的长度为米时,矩形铁皮的面积最大,最大面积是平方米.
【点评】本题考查了二次函数的几何应用、矩形的判定与性质等知识点,熟练掌握二次函数的性质是解题关键.
16.(8分)为响应广州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边露墙,可利用的墙长不超过,另外三边由长的栅栏围成,设矩形空地中,垂直于墙的边,面积为(如图).
(1)求与之间的函数关系式,并写出自变量的取值范围;
(2)若矩形空地的面积为,求的值;
(3)为何值时,有最大值?最大值是多少?
【答案】(1)
(2)
(3),有最大值,最大值是
【分析】(1)根据矩形的面积公式列出y与x之间的函数关系式,并由求出自变量x的取值范围即可;
(2)若矩形空地的面积为,则由可得关于x的一元二次方程,求得方程的解并作出取舍即可;
(3)把(1)中所得的二次函数解析式写成顶点式,根据二次函数的性质可得答案.
【详解】(1)解:根据题意得:,
∵,
∴,
∴y与x之间的函数关系式为;
(2)解:由题意得:,
即,
解得,,
∵,
∴不符合题意,故舍去,
∴;
(3)解:由(1)知,
化成顶点式:,
因为开口向下,x值越靠近对称轴,y值最大,且,
∴当时,y有最大值,且为,
此时,符合题意.
【点评】本题考查了二次函数和一元二次方程的应用,理清题中的数量关系并熟练掌握二次函数的性质是解题的关键.
17.(8分)2023年南宁市公共资源交易中心明确提出将五象站铁路枢纽接入地铁4号线.目前4号线剩余的东段(五象火车站-龙岗站)已经在建设中,施工方决定对终点站龙岗站施工区域中的一条特殊路段进行围挡施工,先沿着路边砌了一堵长的砖墙,然后打算用长的铁皮围栏靠着墙围成中间隔有一道铁皮围栏(平行于)的长方形施工区域.
(1)设施工区域的一边为,施工区域的面积为.请求出S与x的函数关系式,并直接写出自变量x的取值范围;
(2)当围成的施工区域面积为时,的长是多少?
(3)该特殊路段围挡区域的施工成本为400元/,项目方打算拨款120000元用于施工,请你通过计算判断项目方的拨款能否够用.
【答案】(1);
(2)当的长是12米时,围成的施工区域面积为;
(3)拨款够用.理由见解析
【分析】(1)根据题意可得到S与x的函数关系式为:,自变量x的取值范围是:;
(2)当围成的施工区域面积为时:,解一元二次方程即可求得;
(3)由,结合,利用二次函数的性质即可求得最大面积,以及所需费用,即可判断.
【详解】(1)解:根据题意得:,
,
解得:,
∴S与x的函数关系式为:;
(2)解:由(1)知:,
∵围成的施工区域面积为,
∴,
解得:(舍去)或,
∴当的长是12米时,围成的施工区域面积为;
(3)解:拨款够用.解析如下:
∵,
∵,函数图像的对称轴为直线:,
∴当时,S随x的增大而减小,
∴当时,施工区域有最大面积,
所需费用为,
答:拨款够用.
【点评】本题是面积问题(二次函数综合),考查了二次函数的性质及解一元二次方程,熟练掌握二次函数的性质是解决问题的关键.
18.(8分)某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为),另外三面用栅栏围成,中间再用栅栏把它分成两个面积为的矩形,已知栅栏的总长度为.
(1)若矩形养殖场的总面积为36,求长度;
(2)求矩形养殖场的总面积最大值为多少.
【答案】(1)长度为;
(2)矩形养殖场的总面积最大值为.
【分析】1)设,根据题意知:较大矩形的宽为,长为,可得,解方程取符合题意的解,即可得的值为2;
(2)设矩形养殖场的总面积是,根据墙的长度为13,可得,根据题意得出函数解析式,由二次函数性质求最值.
【详解】(1)设,
根据题意知:较大矩形的宽为,长为,
,
解得或,
经检验,时,不符合题意,舍去,
,
答:长度为;
(2)设矩形养殖场的总面积是,
墙的长度为,
,
根据题意得:,
,
当时,取最大值,最大值为,
答:当时,矩形养殖场的总面积最大,最大值为.
【点评】本题考查一元二次方程和二次函数的应用,解题的关键是读懂题意,列出方程及函数关系式.
19.(9分)如图,抛物线与轴交于、,交轴于.
(1)求抛物线的表达式;
(2)是直线上方的抛物线上的一个动点,设的横坐标为,当四边形的面积最大时,求出面积的最大值及点的坐标;
(3)设点是轴上的动点,在平面直角坐标系中,存在点,使得以点为顶点的四边形是菱形,直接写出所有符合条件的点坐标.
【答案】(1)
(2),
(3)或或或
【分析】(1)由三点的坐标,利用待定系数法可求得抛物线的解析式;
(2)过点作轴于点,交于点,连接、,可先求得直线的解析式,则可用分别表示出的坐标,从而可表示出的长,再可用表示出的面积,利用二次函数的性质可求答案;
(3)分和为对角线三种情况,分别根据菱形的性质可求得点的坐标.
【详解】(1)解:∵抛物线经过,,三点,
∴,解得,
∴抛物线的表达式为;
(2)如图1,过点作轴于点,交于点,连接、,
∵,,
∴,
设直线表达式为,
则 ,解得 ,
∴直线表达式为,
∵点的横坐标为,且在抛物线,
∴,
又∵轴于点,交于点,
∴,,
∴,
∴,
∴四边形的面积,
∴当时,取最大值,最大值为,
此时,
∴;
(3)存在.
若为菱形对角线,如下图,
则与互相垂直平分,
∴,
∴;
若为菱形对角线,如下图
则,
∴或;
若为菱形对角线,
则,
设,由,得,
解得,
∴,
∴.
综上可知存在点,使得以点为顶点的四边形是菱形,符合条件的点有4个:或或或.
【点评】本题为二次函数的综合应用,主要考查了待定系数法、勾股定理、二次函数的性质、菱形的性质等知识,运用方程思想和分类讨论思想分析问题是解题关键.
老师对你说:
老师对你说:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学上分层优化堂堂清
二十二章 二次函数
22.3实际问题与二次函数
第一课时 面积问题
学习目标:
1 会求二次函数y=ax2+bx+c的最小(大)值.
2 能够从实际问题中抽象出二次函数关系,并运用二次函数及性质解决最小(大)值等实际问题.
一、利用二次函数解决实际问题的步骤:
1.分析题意,把实际问题转化为数学问题,画出图形.
2.根据已知条件建立适当的平面直角坐标系.
3.选用适当的函数解析式求解.
4.根据二次函数的解析式解决具体的实际问题.
二、利用二次函数解决面积最值的方法:
①找好自变量;
②利用相关的图象面积公式,列出函数关系式;
③利用函数的最值解决面积最值问题。
【注意】自变量的取决范围。
基础提升 教材核心知识点精练
知识点1:求二次函数的最大(最小值)
【例1-1】 已知点在二次函数的图象上,则的最小值为( )
A.-8 B.8 C.-9 D.9
【例1-1】 当时,二次函数的最小值为8,则a的值为( )
A.或5 B.0或6 C.或6 D.0或5
.
知识点2: 图形面积的最值问题
【例2-1】 如图,利用一面长18米的墙,用篱笆围成一个矩形场地,设长为x米,长为y米,且.
(1)若篱笆的长为36米,求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)在(1)的条件下,求出使矩形场地的面积为160平方米的围法.
【例2-2】某家禽养殖场,用总长为200m的围栏靠墙(墙长为65m)围成如图所示的三块矩形区域,矩形EAGH与矩形HGBF面积相等,矩形EAGH面积等于矩形DEFC面积的二分之一,设AD长为xm,矩形区域ABCD的面积为ym2.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,y有最大值?最大值是多少?
(3)现需要在矩形EAGH和矩形DEFC区域分别安装不同种类的养殖设备,单价分别为40元/平方米和20元/平方米,若要使安装成本不超过30000元,请直接写出x的取值范围.
能力强化 能力强化训练
1.如图,在等腰Rt△ABC中,∠C=90°,直角边AC长与正方形MNPQ的边长均为2cm,CA与MN在直线l上.开始时A点与M点重合;让△ABC向右平移;直到C点与N点重合时为止.设△ABC与正方形MNPQ重叠部分(图中阴影部分)的面积为ycm2,MA的长度为xcm,则y与x之间的函数关系大致是( )
A. B.
C. D.
2.如图1,用长的护栏全部建造一个靠墙(墙的长度不限)的矩形养牛场,已知此矩形养牛场的面积为,且与墙垂直的边长为.
(1)此矩形与墙平行的边长为 m(用x来表示);
(2)求y与x之间的函数表达式,并求出此矩形面积的最大值;
(3)如图2,若建造矩形养牛场时,在平行于墙的一边上留了的距离便于出入(不占用护栏材料),当时,该矩形的最大面积为,求a的值.
3 .春回大地,万物复苏,又是一年花季到.某花圃基地计划将如图所示的一块长40 m,宽20 m的矩形空地划分成五块小矩形区域.其中一块正方形空地为育苗区,另一块空地为活动区,其余空地为种植区,分别种植A,B,C三种花卉.活动区一边与育苗区等宽,另一边长是10 m.A,B,C三种花卉每平方米的产值分别是2百元、3百元、4百元.
(1)设育苗区的边长为x m,用含x的代数式表示下列各量:花卉A的种植面积是_____,花卉B的种植面积是______,花卉C的种植面积是_______.
(2)育苗区的边长为多少时,A,B两种花卉的总产值相等?
(3)若花卉A与B的种植面积之和不超过 ,求A,B,C三种花卉的总产值之和的最大值.
堂堂清
一、选择题(每小题4分,共32分)
1.利用长为的墙和长的篱笆来围成一个矩形苗圃园,若平行于墙的一边长不小于,则这个苗圃园面积的最大值和最小值分别为( )
A., B., C., D.,
2.九年级某班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形、等腰直角三角形(底边靠墙)、半圆形这三种方案,如图所示,最佳方案是( )
A.方案1 B.方案2 C.方案3 D.面积都一样
3.如图,要围一个矩形菜园,共中一边是墙,且的长不能超过,其余的三边用篱笆,且这三边的和为.有下列结论:
①的长可以为;
②的长有两个不同的值满足菜园面积为;
③菜园面积的最大值为.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
4.如图1所示的矩形窗框的周长及其两条隔断、的总长为米,且隔断、分别与矩形的两条邻边平行,设的长为米,矩形的面积为平方米,关于的函数图像如图2,则下列说法正确的是( )
A.矩形的最大面积为8平方米 B.与之间的函数关系式为
C.当时,矩形的面积最大 D.的值为12
5.如图1,一张边长为、的长方形纸片的面积等于,将它通过割、拼,再补一个正方形,拼成一个新的正方形(如图2),可以取得的最小整数是( )
A. B. C. D.3
6.如图,四边形中,,若,则四边形的面积最大值是( )
A.4 B.6 C.8 D.10
7.如图,晓波家的院墙一边靠墙处,用米长的铁栅栏围成了三个相连的养殖小院子,总面积为平方米,为方便喂养这些不同类的动物,在各个养殖院子之间留出了米宽的缺口作通道,在平行于墙的一边留下一个米宽的缺口作小门.若设米,则关于的函数关系式为( )
A. B.
C. D.
8.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的两处各留宽的门.已知计划中的材料可建墙体(不包括门)总长为,则当能建成的饲养室总占地面积最大时,中间隔开的墙长是( )米.
A.4 B.5 C.6 D.8
二、填空题(每小题4分,共20分)
9.如图,王叔叔想用长为的栅栏,再借助房屋的外墙围成一个矩形羊圈,已知房屋外墙足够长,当矩形的边 时,羊圈的面积最大.
10.如图,P是抛物线在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形周长的最大值为 .
11.长方形的周长为,其中一边长为(其中),面积为,则与的关系式为 .
12.如图,某活动板房由矩形和抛物线构成,矩形的边长,,抛物线的最高点E到BC的距离为.在该抛物线与之间的区域内装有一扇矩形窗户,点G、H在边上,点F、K在该抛物线上.按如图所示建立平面直角坐标系.若,则矩形窗户的宽的长为 m.
13.如图,有一矩形纸片,长、宽分别为厘米和厘米,现在长宽上分别剪去宽为厘米()的纸条,则剩余部分(图中阴影部分)的面积关于的函数关系式为 .
三、解答题(共48分)
14.如图,要利用一面墙(长为)建羊圈,用100m长的围栏围成两个大小相同的矩形羊圈,每个羊圈留有个宽的门(留门部分不需要围栏),若宽用x(m)表示,总面积用y()表示.
(1)写出总面积y()关于宽x(m)的函数关系式:
(2)当面积时,求羊圈的宽x的值.
15.工匠师傅准备从六边形的铁皮中,裁出一块矩形铁皮制作工件,如图所示.经测量,,与之间的距离为2米,米,米,,.,,是工匠师傅画出的裁剪虚线.当的长度为多少时,矩形铁皮的面积最大,最大面积是多少?
16.为响应广州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边露墙,可利用的墙长不超过,另外三边由长的栅栏围成,设矩形空地中,垂直于墙的边,面积为(如图).
(1)求与之间的函数关系式,并写出自变量的取值范围;
(2)若矩形空地的面积为,求的值;
(3)为何值时,有最大值?最大值是多少?
17.2023年南宁市公共资源交易中心明确提出将五象站铁路枢纽接入地铁4号线.目前4号线剩余的东段(五象火车站-龙岗站)已经在建设中,施工方决定对终点站龙岗站施工区域中的一条特殊路段进行围挡施工,先沿着路边砌了一堵长的砖墙,然后打算用长的铁皮围栏靠着墙围成中间隔有一道铁皮围栏(平行于)的长方形施工区域.
(1)设施工区域的一边为,施工区域的面积为.请求出S与x的函数关系式,并直接写出自变量x的取值范围;
(2)当围成的施工区域面积为时,的长是多少?
(3)该特殊路段围挡区域的施工成本为400元/,项目方打算拨款120000元用于施工,请你通过计算判断项目方的拨款能否够用.
18.某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为),另外三面用栅栏围成,中间再用栅栏把它分成两个面积为的矩形,已知栅栏的总长度为.
(1)若矩形养殖场的总面积为36,求长度;
(2)求矩形养殖场的总面积最大值为多少.
19.如图,抛物线与轴交于、,交轴于.
(1)求抛物线的表达式;
(2)是直线上方的抛物线上的一个动点,设的横坐标为,当四边形的面积最大时,求出面积的最大值及点的坐标;
(3)设点是轴上的动点,在平面直角坐标系中,存在点,使得以点为顶点的四边形是菱形,直接写出所有符合条件的点坐标.
九年级数学上分层优化堂堂清
二十二章 二次函数
22.3实际问题与二次函数
第一课时 面积问题 (解析版)
学习目标:
1 会求二次函数y=ax2+bx+c的最小(大)值.
2 能够从实际问题中抽象出二次函数关系,并运用二次函数及性质解决最小(大)值等实际问题.
一、利用二次函数解决实际问题的步骤:
1.分析题意,把实际问题转化为数学问题,画出图形.
2.根据已知条件建立适当的平面直角坐标系.
3.选用适当的函数解析式求解.
4.根据二次函数的解析式解决具体的实际问题.
二、利用二次函数解决面积最值的方法:
①找好自变量;
②利用相关的图象面积公式,列出函数关系式;
③利用函数的最值解决面积最值问题。
【注意】自变量的取决范围。
基础提升 教材核心知识点精练
知识点1:求二次函数的最大(最小值
【例1-1】 已知点在二次函数的图象上,则的最小值为( )
A.-8 B.8 C.-9 D.9
【答案】C
【分析】根据点在函数图象上可得,继而可得,由二次函数的最值即可得出答案.
【详解】解:依题意得:,
∴
∴当时,有最小值为,
故选:C.
【点评】本题主要考查了函数图象上点的特征,正确得出是解题关键.
【例1-1】 当时,二次函数的最小值为8,则a的值为( )
A.或5 B.0或6 C.或6 D.0或5
【答案】C
【分析】由,可知二次函数对称轴为直线,且图象开口向上,当时,,计算求出满足要求的值即可;当,即时,,计算求出满足要求的值即可.
【详解】解:,
∴二次函数对称轴为直线,且图象开口向上,
∴当时,,解得,或(舍去),
当,即时,,解得,或(舍去),
综上,a的值为或6,
故选:C.
【点评】本题考查了二次函数的图象与性质,二次函数的最值.解题的关键在于对知识的熟练掌握与灵活运用.
知识点2: 图形面积的最值问题
【例2-1】 如图,利用一面长18米的墙,用篱笆围成一个矩形场地,设长为x米,长为y米,且.
(1)若篱笆的长为36米,求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)在(1)的条件下,求出使矩形场地的面积为160平方米的围法.
【答案】(1),
(2)长为16米,长为10米
【分析】(1)由图可知篱笆长,把相关数值代入即可求解;
(2)列出矩形面积S与x的关系式,再令,求出方程的解,可得结果.
【详解】(1)解:,
,
.
,,
,
,
又,
,
.
(2)设矩形的面积为,
则,
当时得:
,解得:,,
,
,
,,
答:当长为16米,长为10米时,矩形的面积为160平方米.
【点评】此题考查了二次函数的应用,不仅是一道实际问题,而且结合了矩形的性质,解答此题要注意以下问题:(1)矩形的一边为墙,且墙的长度不超过18米;(2)根据矩形的面积公式列一元二次方程并根据根的判别式来判断是否两边长相等.
【例2-2】某家禽养殖场,用总长为200m的围栏靠墙(墙长为65m)围成如图所示的三块矩形区域,矩形EAGH与矩形HGBF面积相等,矩形EAGH面积等于矩形DEFC面积的二分之一,设AD长为xm,矩形区域ABCD的面积为ym2.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,y有最大值?最大值是多少?
(3)现需要在矩形EAGH和矩形DEFC区域分别安装不同种类的养殖设备,单价分别为40元/平方米和20元/平方米,若要使安装成本不超过30000元,请直接写出x的取值范围.
【解答】解:(1)由题意得,AE=HG=AD=xm,
DC=AB=(200﹣x)=(100﹣x)m,
故y=x(100﹣x)=﹣x2+100x,
自变量x的取值范围为:28≤x<80;
(2)由题意可得:
∵y=﹣x2+100x=﹣( x2﹣80x)=﹣( x﹣40)2+2000,
又∵28≤x<80,
∴当x=40时,y有最大值,最大值为2000平方米;
(3)由题意得,S矩形EAGH=AG AE=(100﹣x)x=﹣x2+25x,S矩形DEFC=DC DE=(100﹣x) x=﹣x2+50x,
设安装成本为w元,则w=40(﹣x2+25x)+20(﹣x2+50x)=﹣25x2+2000x,
令w=30000,则﹣25x2+2000x=30000,
解得x=60或20,
∵28≤x<80,
∴60≤x<80时,安装成本不超过30000元.
能力强化 能力强化训练
1.如图,在等腰Rt△ABC中,∠C=90°,直角边AC长与正方形MNPQ的边长均为2cm,CA与MN在直线l上.开始时A点与M点重合;让△ABC向右平移;直到C点与N点重合时为止.设△ABC与正方形MNPQ重叠部分(图中阴影部分)的面积为ycm2,MA的长度为xcm,则y与x之间的函数关系大致是( )
A. B.
C. D.
【答案】C
【分析】根据动点的运动过程确定每段阴影部分与x的关系类型,根据函数的性质确定选项.
【详解】解:当x≤2cm时,重合部分是边长为x的等腰直角三角形,
面积为:y=x2,
是一个开口向上的二次函数;
当x>2时,
重合部分是直角梯形,
面积为:y=8﹣(x﹣2)2,
是一个开口向下的二次函数,
故选:C.
【点评】本题是对函数图像的考查,熟练掌握图像的面积及函数知识是解决本题的关键.
2.如图1,用长的护栏全部建造一个靠墙(墙的长度不限)的矩形养牛场,已知此矩形养牛场的面积为,且与墙垂直的边长为.
(1)此矩形与墙平行的边长为 m(用x来表示);
(2)求y与x之间的函数表达式,并求出此矩形面积的最大值;
(3)如图2,若建造矩形养牛场时,在平行于墙的一边上留了的距离便于出入(不占用护栏材料),当时,该矩形的最大面积为,求a的值.
【答案】(1)
(2)450
(3)4
【分析】(1)将长的护栏减去即可;
(2)根据矩形的面积定义长乘以宽,即可求出y与x之间的函数表达式,由二次函数的顶点坐标即可求出矩形面积的最大值;
(3)先求出y与x之间的函数表达式,再求出,由矩形的最大面积为,得,解出a的值,舍去负数,即可得答案.
【详解】(1)解:由题意得:此矩形与墙平行的边长为;
故答案为:
(2),
y与x之间的函数表达式是,矩形面积的最大值450;
(3),
二次函数的对称轴,
,
,
,
矩形的最大面积为,
,
解得:或(舍去),
.
【点评】本题考查了二次函数在实际问题中的应用,根据题意正确得出函数关系式并明确二次函数的性质是解题的关键.
3 .春回大地,万物复苏,又是一年花季到.某花圃基地计划将如图所示的一块长40 m,宽20 m的矩形空地划分成五块小矩形区域.其中一块正方形空地为育苗区,另一块空地为活动区,其余空地为种植区,分别种植A,B,C三种花卉.活动区一边与育苗区等宽,另一边长是10 m.A,B,C三种花卉每平方米的产值分别是2百元、3百元、4百元.
(1)设育苗区的边长为x m,用含x的代数式表示下列各量:花卉A的种植面积是_____,花卉B的种植面积是______,花卉C的种植面积是_______.
(2)育苗区的边长为多少时,A,B两种花卉的总产值相等?
(3)若花卉A与B的种植面积之和不超过 ,求A,B,C三种花卉的总产值之和的最大值.
【答案】(1);;
(2)32m或10m
(3)168000元
【分析】(1)根据正方形和长方形的面积计算公式可直接得到答案;
(2)根据A,B两种花卉的总产值相等建立一元二次方程,解方程即可得到答案;
(3)先根据花卉A与B的种植面积之和不超过建立不等式,得到,再设A,B,C三种花卉的总产值之和y百元,得到y关于x的二次函数,根据二次函数的图形性质即可得到答案.
【详解】(1)解:∵育苗区的边长为x m,活动区的边长为10m,
∴花卉A的面积为: ,
花卉B的面积为: ,
花卉C的面积为: ,
故答案为:;;;
(2)解:∵A,B花卉每平方米的产值分别是2百元、3百元,
∴A,B两种花卉的总产值分别为百元和百元,
∵A,B两种花卉的总产值相等,
∴,
∴,
解方程得或,
∴当育苗区的边长为32m或10m时,A,B两种花卉的总产值相等;
(3)解:∵花卉A与B的种植面积之和为: ,
∴,
∴,
∵设A,B,C三种花卉的总产值之和y百元,
∴,
∴,
∴,
∴当时,y随x的增加而减小,
∴当时,y最大,且(百元),
故A,B,C三种花卉的总产值之和的最大值168000元.
【点评】本题考查一元二次方程和二次函数的应用,解题的关键是根据题意建立正确的方程和函数表达式.
堂堂清
一、选择题(每小题4分,共32分)
利用长为的墙和长的篱笆来围成一个矩形苗圃园,若平行于墙的一边长不小于,则这个苗圃园面积的最大值和最小值分别为( )
A., B., C., D.,
【答案】.A
【分析】设垂直于墙的一边长为,则平行于墙的一边长为,矩形面积为,先根据平行于墙的长度不小于,墙的长度为求出,再根据矩形面积公式求出,由此利用二次函数的性质求解即可.
【详解】解;设垂直于墙的一边长为,则平行于墙的一边长为,矩形面积为,
∵平行于墙的一边长不小于,墙的长度为
∴,
∴,
,
∵,
∴当时,y随x增大而减小,
∴当时,,
当时,,
∴这个苗圃园面积的最大值和最小值分别为,,
故选A.
【点评】本题主要考查了二次函数的实际应用,一元一次不等式组的实际应用,正确求出矩形面积与垂直于墙的一边的二次函数关系式是解题的关键.
2.九年级某班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形、等腰直角三角形(底边靠墙)、半圆形这三种方案,如图所示,最佳方案是( )
A.方案1 B.方案2 C.方案3 D.面积都一样
【答案】C
【分析】根据二次函数的性质,分别计算出三个方案的菜园面积进行比较即可.
【详解】解:方案1:设米,则米,
则菜园面积,
当时,此时菜园最大面积为8平方米;
方案2:如图,,
∵,
∴菜园面积为8平方米;
方案3:半圆的半径为米,
∴此时菜园最大面积(平方米)
∵,
∴方案3的菜园面积最大,
∴在三种方案中,最佳方案是方案3.
故选:C.
【点评】本题考查了二次函数的应用、圆的面积、等腰三角形的性质,根据题意计算三个方案的边长及半径是解本题的关键.
3.如图,要围一个矩形菜园,共中一边是墙,且的长不能超过,其余的三边用篱笆,且这三边的和为.有下列结论:
①的长可以为;
②的长有两个不同的值满足菜园面积为;
③菜园面积的最大值为.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
【答案】C
【分析】设的长为,矩形的面积为,则的长为,根据矩形的面积公式列二次函数解析式,再分别根据的长不能超过,二次函数的最值,解一元二次方程求解即可.
【详解】设的长为,矩形的面积为,则的长为,由题意得
,
其中,即,
①的长不可以为,原说法错误;
③菜园面积的最大值为,原说法正确;
②当时,解得或,
∴的长有两个不同的值满足菜园面积为,说法正确;
综上,正确结论的个数是2个,
故选:C.
【点评】本题考查了二次函数的应用,解一元二次方程,准确理解题意,列出二次函数解析式是解题的关键.
4.如图1所示的矩形窗框的周长及其两条隔断、的总长为米,且隔断、分别与矩形的两条邻边平行,设的长为米,矩形的面积为平方米,关于的函数图像如图2,则下列说法正确的是( )
A.矩形的最大面积为8平方米 B.与之间的函数关系式为
C.当时,矩形的面积最大 D.的值为12
【答案】D
【分析】观察图2,得出当时,函数值最大,根据题意确定a的值,并可求出二次函数解析式,即可做出正确判断.
【详解】解:由图2可知,函数图像最高点为,经过原点,
设二次函数解析式为,
代入,解得,
由此判断:A.矩形最大面积是4平方米,选项错误;
B.二次函数解析式为,选项错误;
C.矩形面积最大时,,选项错误;
D.当时,矩形面积取最大值,,,选项正确.
故选:D.
【点评】本题考查二次函数图像和性质,解题的关键是识别函数图像,确定自变量的取值为何值时函数取得最大值,并利用待定系数法求得函数解析式.
5.如图1,一张边长为、的长方形纸片的面积等于,将它通过割、拼,再补一个正方形,拼成一个新的正方形(如图2),可以取得的最小整数是( )
A. B. C. D.3
【答案】B
【分析】利用长方形的面积公式,可得出关于的函数关系式,再利用二次函数的性质,即可解决最值问题.
【详解】解:根据题意得:,
,
.
,且,
当时,随的增大而增大,
当时,可以取得最小整数,此时.
故选:B.
【点评】本题考查了二次函数的性质以及二次函数的最值,根据各数量之间的关系,找出k关于a的函数关系式是解题的关键.
6.如图,四边形中,,若,则四边形的面积最大值是( )
A.4 B.6 C.8 D.10
【答案】C
【分析】设,,根据题意表示四边形的面积,根据二次函数的性质作答即可.
【详解】解:如图,设、交于点M,
设,
,
,
由题意,得:四边形的面积为,
即四边形的面积,
∴当时,四边形的面积最大,最大为8.
故选:C.
【点评】本题考查了二次函数与几何的综合应用.根据题意,将四边形的面积问题转化为二次函数求最值问题,是解题的关键.
7.如图,晓波家的院墙一边靠墙处,用米长的铁栅栏围成了三个相连的养殖小院子,总面积为平方米,为方便喂养这些不同类的动物,在各个养殖院子之间留出了米宽的缺口作通道,在平行于墙的一边留下一个米宽的缺口作小门.若设米,则关于的函数关系式为( )
A. B.
C. D.
【答案】D
【分析】如图所示(见详解),设米,则可求出的长,根据矩形的面积公式即可求解.
【详解】解:如图所示,
设米,则,
又小院子的总面积为,
∴,
故选:.
【点评】本题主要考查二次函数的运用,理解图形面积的计算方法,掌握数量关系,准确列出函数关系式是解题的关键.
8.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的两处各留宽的门.已知计划中的材料可建墙体(不包括门)总长为,则当能建成的饲养室总占地面积最大时,中间隔开的墙长是( )米.
A.4 B.5 C.6 D.8
【答案】B
【分析】根据题意,设能建成的饲养室总占地的面积为,根据二次函数的性质即可求解.
【详解】解:设中间隔开的墙长为,能建成的饲养室总占地的面积为,
根据题意得,,,有最大值,
∴当时,取得最大值,
故选:B.
【点评】本题考查了二次函数的应用,根据题意列出函数关系式是解题的关键.
二、填空题(每小题4分,共20分
9.如图,王叔叔想用长为的栅栏,再借助房屋的外墙围成一个矩形羊圈,已知房屋外墙足够长,当矩形的边 时,羊圈的面积最大.
【答案】15
【分析】设为,则,根据矩形的面积公式可得关于x的二次函数关系式,配方后即可解.
【详解】解:设为,面积为,
由题意可得:,
当时,取得最大值,
即时,羊圈的面积最大,
故答案为:.
【点评】本题考查了二次函数的性质在实际生活中的应用.最大面积的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.其中要注意应该在自变量的取值范围内求最大值(或最小值),也就是说二次函数的最值不一定在时取得.
10.如图,P是抛物线在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形周长的最大值为 .
【答案】/12.5
【分析】设点P的坐标为,,根据四边形的周长得到:,再由二次函数的性质即可求得最大值.
【详解】解:设点P的坐标为,,
由题意可知:四边形的周长,
∴,
当时,C有最大值.
故答案为:.
【点评】本题考查了二次函数的最值及二次函数的图像上点的坐标特征,最后根据二次函数的性质求最值是解题的关键.
11.长方形的周长为,其中一边长为(其中),面积为,则与的关系式为 .
【答案】
【分析】首先利长方形周长公式表示出长方形的另一边长,然后利用长方形的面积公式求解.
【详解】解:∵长方形的周长为,长方形的一边长为,
∴另一边长为,
则与的关系式为,
故答案为:.
【点评】本题考查了列函数关系式,理解长方形的边长、周长以及面积之间的关系是关键.
12.如图,某活动板房由矩形和抛物线构成,矩形的边长,,抛物线的最高点E到BC的距离为.在该抛物线与之间的区域内装有一扇矩形窗户,点G、H在边上,点F、K在该抛物线上.按如图所示建立平面直角坐标系.若,则矩形窗户的宽的长为 m.
【答案】/
【分析】利用待定系数法求出抛物线解析式,设,求出,即可得到矩形窗户的宽的长.
【详解】解:由题意可知,、、,
设抛物线解析式为,
,解得:
抛物线解析式为,
点G、H在边上,且,
、,
四边形是矩形,
设,
点在抛物线上,
,
,
故答案为:.
【点评】本题考查了坐标与图形,待定系数法求函数解析式,矩形的性质,二次函数的性质等知识,求出二次函数解析式,掌握二次函数的性质是解题关键.
13.如图,有一矩形纸片,长、宽分别为厘米和厘米,现在长宽上分别剪去宽为厘米()的纸条,则剩余部分(图中阴影部分)的面积关于的函数关系式为 .
【答案】
【分析】阴影部分的长方形的的长为,宽为,然后根据长方形的面积公式即可求解.
【详解】阴影部分的长方形的的长为,宽为,
所以面积.
【点评】本题考查了利用长方形的面积公式列出函数关系式,其中根据题意,找到所求量的等量关系是解决问题的关键.
三、解答题(共48分)
14.(8分)如图,要利用一面墙(长为)建羊圈,用100m长的围栏围成两个大小相同的矩形羊圈,每个羊圈留有个宽的门(留门部分不需要围栏),若宽用x(m)表示,总面积用y()表示.
(1)写出总面积y()关于宽x(m)的函数关系式:
(2)当面积时,求羊圈的宽x的值.
【答案】(1)
(2)羊圈的宽x的值为26米
【分析】(1)根据长方形面积公式求解即可;
(2)把代入(1)中的解析式,解一元二次方程求解即可.
【详解】(1)由题意得,,
∵,
∴,
∵,
∴,
∴;
(2)当时,
解得(不合题意,舍去),
∴羊圈的宽x的值为26米.
【点评】本题考查了二次函数的应用和解一元二次方程,准确理解题意,熟练掌握解方程的方法是解题的关键.
15.(7分)工匠师傅准备从六边形的铁皮中,裁出一块矩形铁皮制作工件,如图所示.经测量,,与之间的距离为2米,米,米,,.,,是工匠师傅画出的裁剪虚线.当的长度为多少时,矩形铁皮的面积最大,最大面积是多少?
【答案】当的长度为米时,矩形铁皮的面积最大,最大面积是平方米
【分析】连接,分别交于点,交于点,先判断出四边形是矩形,从而可得,再判断出四边形和四边形都是矩形,从而可得米,,然后设矩形的面积为平方米,米,则米,米,利用矩形的面积公式可得关于的二次函数,最后利用二次函数的性质求解即可得.
【详解】解:如图,连接,分别交于点,交于点,
,
,
米,
四边形是平行四边形,
又,
四边形是矩形,
,,
,
,
四边形是矩形,
,
四边形和四边形都是矩形,
米,,
和都是等腰直角三角形,
,
,
设矩形的面积为平方米,米,则米,米,
米,
米,
,
又,与之间的距离为2米,米,
,
由二次函数的性质可知,当时,随的增大而增大;当时,随的增大而减小,
则当时,取得最大值,最大值为,
答:当的长度为米时,矩形铁皮的面积最大,最大面积是平方米.
【点评】本题考查了二次函数的几何应用、矩形的判定与性质等知识点,熟练掌握二次函数的性质是解题关键.
16.(8分)为响应广州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边露墙,可利用的墙长不超过,另外三边由长的栅栏围成,设矩形空地中,垂直于墙的边,面积为(如图).
(1)求与之间的函数关系式,并写出自变量的取值范围;
(2)若矩形空地的面积为,求的值;
(3)为何值时,有最大值?最大值是多少?
【答案】(1)
(2)
(3),有最大值,最大值是
【分析】(1)根据矩形的面积公式列出y与x之间的函数关系式,并由求出自变量x的取值范围即可;
(2)若矩形空地的面积为,则由可得关于x的一元二次方程,求得方程的解并作出取舍即可;
(3)把(1)中所得的二次函数解析式写成顶点式,根据二次函数的性质可得答案.
【详解】(1)解:根据题意得:,
∵,
∴,
∴y与x之间的函数关系式为;
(2)解:由题意得:,
即,
解得,,
∵,
∴不符合题意,故舍去,
∴;
(3)解:由(1)知,
化成顶点式:,
因为开口向下,x值越靠近对称轴,y值最大,且,
∴当时,y有最大值,且为,
此时,符合题意.
【点评】本题考查了二次函数和一元二次方程的应用,理清题中的数量关系并熟练掌握二次函数的性质是解题的关键.
17.(8分)2023年南宁市公共资源交易中心明确提出将五象站铁路枢纽接入地铁4号线.目前4号线剩余的东段(五象火车站-龙岗站)已经在建设中,施工方决定对终点站龙岗站施工区域中的一条特殊路段进行围挡施工,先沿着路边砌了一堵长的砖墙,然后打算用长的铁皮围栏靠着墙围成中间隔有一道铁皮围栏(平行于)的长方形施工区域.
(1)设施工区域的一边为,施工区域的面积为.请求出S与x的函数关系式,并直接写出自变量x的取值范围;
(2)当围成的施工区域面积为时,的长是多少?
(3)该特殊路段围挡区域的施工成本为400元/,项目方打算拨款120000元用于施工,请你通过计算判断项目方的拨款能否够用.
【答案】(1);
(2)当的长是12米时,围成的施工区域面积为;
(3)拨款够用.理由见解析
【分析】(1)根据题意可得到S与x的函数关系式为:,自变量x的取值范围是:;
(2)当围成的施工区域面积为时:,解一元二次方程即可求得;
(3)由,结合,利用二次函数的性质即可求得最大面积,以及所需费用,即可判断.
【详解】(1)解:根据题意得:,
,
解得:,
∴S与x的函数关系式为:;
(2)解:由(1)知:,
∵围成的施工区域面积为,
∴,
解得:(舍去)或,
∴当的长是12米时,围成的施工区域面积为;
(3)解:拨款够用.解析如下:
∵,
∵,函数图像的对称轴为直线:,
∴当时,S随x的增大而减小,
∴当时,施工区域有最大面积,
所需费用为,
答:拨款够用.
【点评】本题是面积问题(二次函数综合),考查了二次函数的性质及解一元二次方程,熟练掌握二次函数的性质是解决问题的关键.
18.(8分)某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为),另外三面用栅栏围成,中间再用栅栏把它分成两个面积为的矩形,已知栅栏的总长度为.
(1)若矩形养殖场的总面积为36,求长度;
(2)求矩形养殖场的总面积最大值为多少.
【答案】(1)长度为;
(2)矩形养殖场的总面积最大值为.
【分析】1)设,根据题意知:较大矩形的宽为,长为,可得,解方程取符合题意的解,即可得的值为2;
(2)设矩形养殖场的总面积是,根据墙的长度为13,可得,根据题意得出函数解析式,由二次函数性质求最值.
【详解】(1)设,
根据题意知:较大矩形的宽为,长为,
,
解得或,
经检验,时,不符合题意,舍去,
,
答:长度为;
(2)设矩形养殖场的总面积是,
墙的长度为,
,
根据题意得:,
,
当时,取最大值,最大值为,
答:当时,矩形养殖场的总面积最大,最大值为.
【点评】本题考查一元二次方程和二次函数的应用,解题的关键是读懂题意,列出方程及函数关系式.
19.(9分)如图,抛物线与轴交于、,交轴于.
(1)求抛物线的表达式;
(2)是直线上方的抛物线上的一个动点,设的横坐标为,当四边形的面积最大时,求出面积的最大值及点的坐标;
(3)设点是轴上的动点,在平面直角坐标系中,存在点,使得以点为顶点的四边形是菱形,直接写出所有符合条件的点坐标.
【答案】(1)
(2),
(3)或或或
【分析】(1)由三点的坐标,利用待定系数法可求得抛物线的解析式;
(2)过点作轴于点,交于点,连接、,可先求得直线的解析式,则可用分别表示出的坐标,从而可表示出的长,再可用表示出的面积,利用二次函数的性质可求答案;
(3)分和为对角线三种情况,分别根据菱形的性质可求得点的坐标.
【详解】(1)解:∵抛物线经过,,三点,
∴,解得,
∴抛物线的表达式为;
(2)如图1,过点作轴于点,交于点,连接、,
∵,,
∴,
设直线表达式为,
则 ,解得 ,
∴直线表达式为,
∵点的横坐标为,且在抛物线,
∴,
又∵轴于点,交于点,
∴,,
∴,
∴,
∴四边形的面积,
∴当时,取最大值,最大值为,
此时,
∴;
(3)存在.
若为菱形对角线,如下图,
则与互相垂直平分,
∴,
∴;
若为菱形对角线,如下图
则,
∴或;
若为菱形对角线,
则,
设,由,得,
解得,
∴,
∴.
综上可知存在点,使得以点为顶点的四边形是菱形,符合条件的点有4个:或或或.
【点评】本题为二次函数的综合应用,主要考查了待定系数法、勾股定理、二次函数的性质、菱形的性质等知识,运用方程思想和分类讨论思想分析问题是解题关键.
老师对你说:
老师对你说:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
