九年级数学上分层优化堂堂清(11)22.3 实际问题与二次函数——抛物线型问题(含解析)
文档属性
| 名称 | 九年级数学上分层优化堂堂清(11)22.3 实际问题与二次函数——抛物线型问题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
九年级数学上分层优化堂堂清
二十二章 二次函数
22.3实际问题与二次函数
第三课时 抛物线型问题
学习目标:
1.能够从实际问题中抽象出二次函数模型,并运用二次函数及性质解决实际问题;
2.在探究二次函数的实际应用中学会分析问题,体会数学建模思想以及数学与生活的紧密联系性。
用二次函数解决抛物线型的一般步骤:
(1)恰当地建立直角坐标系;
(2)将已知条件转化为点的坐标;
(3)合理地设出所求函数关系式;
(4)代入已知条件或点的坐标,求出关系式;
(5)利用关系式求解问题.
二、利用二次函数解决抛物线型问题具体思路
这类问题所给的问题情境常有一个抛物线型物体,比如拱桥或隧道这些问题都可以通过构造二次承数的表达式来解决,解决这类问题般是利用数形结合思想和函数思想。
1.一般解题思路
(1)在示意图中建立适当的平面直角坐标系,将题目中所给条件转化平面直角坐标系中的坐标。
(2)根据图中坐标利用待定系数法求得二次函数的表达式。
(3)由二次函数的性质去分析解决问题,检验问题的结果是否符合实标意义,并作答。
2.卡车过拱桥(隧道)问题
在问题中,抛物线的函数表达式是首要条件,有时函数表达式已经给出,有时需要先求出来,求出函数表达式后有两种方法可以判断卡车能否从桥下通过:
(1)固定卡车的宽,看桥是否足够高(即相当于已知x的值,根据函数表达式求y的值,然后与限制的高的值比较大小);
(2)固定卡车的高,看桥是否足够宽(即相当于已知y的值,根据函数表达式求x的值,然后与限制的宽的值比较大小)
基础提升 教材核心知识点精练
知识点1:拱桥问题
【例1-1】郑州市彩虹桥新桥将于2023年9月底建成通车.新桥采用三跨连续单拱肋钢箱系杆拱桥,既保留了历史记忆,又展示出郑州的开放与创新.新桥的中跨大拱的拱肋可视为抛物线的一部分,桥面(视为水平的)与拱肋用垂直于桥面的系杆连接,测得拱肋的跨度为120米,与中点O相距30米处有一高度为27米的系杆.以所在直线为x轴,抛物线的对称轴为y轴建立如图②所示的平面直角坐标系.
(1)求抛物线的解析式;
(2)正中间系杆的长度是多少米?若相邻系杆之间的间距均为3米(不考虑系杆的粗细),是否存在一根系杆的长度恰好是长度的?请说明理由.
【例1-2】如图,有一个横截面为抛物线形状的隧道,隧道底部宽为,拱顶内高.把截面图形放在如图所示的平面直角坐标系中(原点O是的中点).
(1)求这条抛物线所对应的函数表达式;
(2)如果该隧道设计为车辆双向通行,规定车辆必须在中心黄线两侧行驶,那么一辆宽,高的大型货运卡车是否可以通过?为什么?
知识点2:投球问题
【例2-1】掷实心球是中考体育考试项目之一.如图1是一名男生掷实心球情境,实心球行进路线是一条抛物线,行进高度与水平距离之间的函数关系如图2所示.掷出时,起点处高度为.当水平距离为时,实心球行进至最高点处.
(1)求y关于x的函数表达式;
(2)根据中考体育考试评分标准(男生版),投掷过程中,实心球从起点到落地点的水平距离大于等于时,即可得满分10分.该男生在此项考试中能否得满分,请说明理由.
【例2-2】实心球是中考体育项目之一.在掷实心球时,实心球被掷出后的运动路线可以看作是抛物线的一部分,已知小军在一次掷实心球训练中,第一次投掷时出手点距地面1.8m,实心球运动至最高点时距地面3.4m,距出手点的水平距离为4m.设实心球掷出后距地面的竖直高度为y(m),实心球距出手点的水平距离为x(m).如图,以水平方向为x轴,出手点所在竖直方向为y轴建立平面直角坐标系.
(1)求第一次掷实心球时运动路线所在抛物线的表达式.
(2)若实心球投掷成绩(即出手点与着陆点的水平距离)达到12.4m为满分,请判断小军第一次投掷实心球能否得满分.
(3)第二次投掷时,实心球运动的竖直高度y与水平距离x近似满足函数关系.记小军第一次投掷时出手点与着陆点的水平距离为,第二次投掷时出手点与着陆点的水平距离为,则______(填“>”“<”“=”).
知识点3:喷水问题
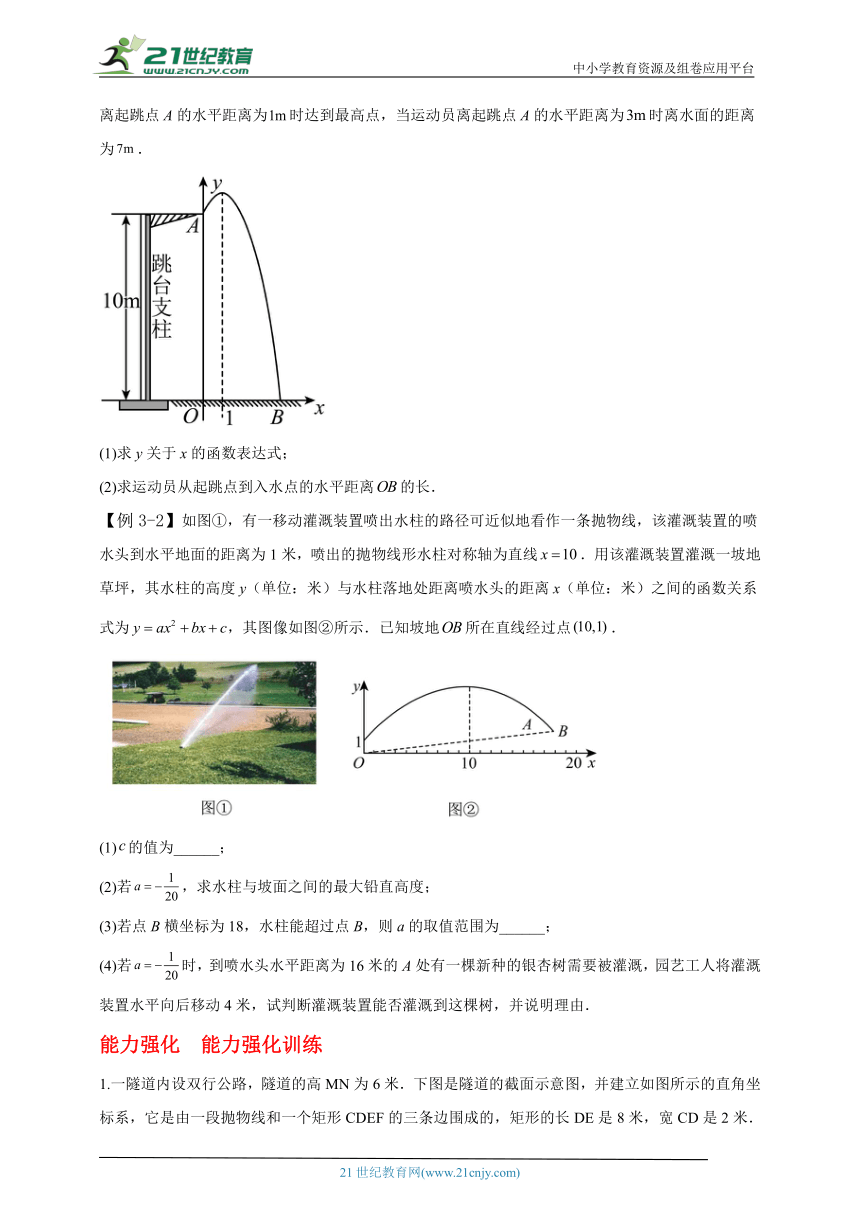
【例3-1】一名运动员在高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面的高度与离起跳点A的水平距离之间的函数关系如图所示,运动员离起跳点A的水平距离为时达到最高点,当运动员离起跳点A的水平距离为时离水面的距离为.
(1)求y关于x的函数表达式;
(2)求运动员从起跳点到入水点的水平距离的长.
【例3-2】如图①,有一移动灌溉装置喷出水柱的路径可近似地看作一条抛物线,该灌溉装置的喷水头到水平地面的距离为1米,喷出的抛物线形水柱对称轴为直线.用该灌溉装置灌溉一坡地草坪,其水柱的高度y(单位:米)与水柱落地处距离喷水头的距离x(单位:米)之间的函数关系式为,其图像如图②所示.已知坡地所在直线经过点.
(1)的值为______;
(2)若,求水柱与坡面之间的最大铅直高度;
(3)若点B横坐标为18,水柱能超过点B,则a的取值范围为______;
(4)若时,到喷水头水平距离为16米的A处有一棵新种的银杏树需要被灌溉,园艺工人将灌溉装置水平向后移动4米,试判断灌溉装置能否灌溉到这棵树,并说明理由.
能力强化 能力强化训练
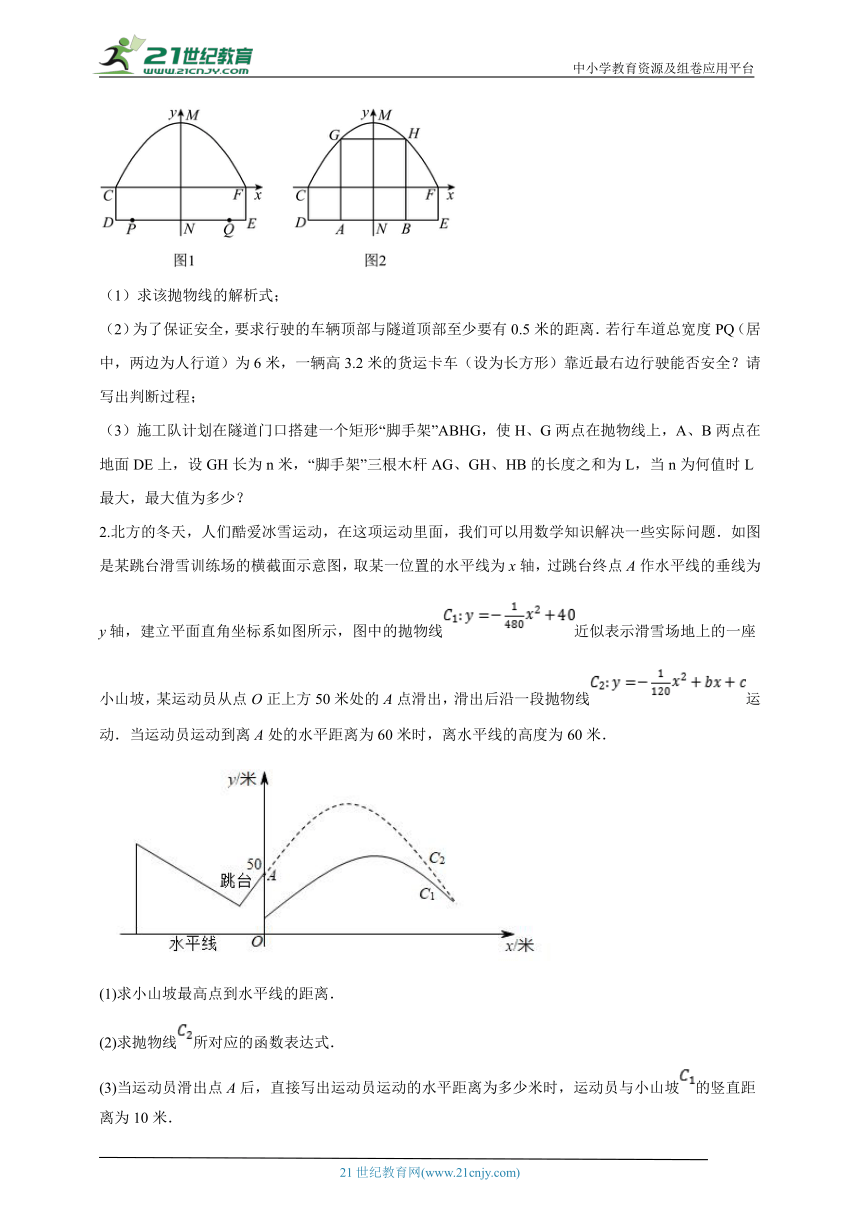
1.一隧道内设双行公路,隧道的高MN为6米.下图是隧道的截面示意图,并建立如图所示的直角坐标系,它是由一段抛物线和一个矩形CDEF的三条边围成的,矩形的长DE是8米,宽CD是2米.
(1)求该抛物线的解析式;
(2)为了保证安全,要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离.若行车道总宽度PQ(居中,两边为人行道)为6米,一辆高3.2米的货运卡车(设为长方形)靠近最右边行驶能否安全?请写出判断过程;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABHG,使H、G两点在抛物线上,A、B两点在地面DE上,设GH长为n米,“脚手架”三根木杆AG、GH、HB的长度之和为L,当n为何值时L最大,最大值为多少?
2.北方的冬天,人们酷爱冰雪运动,在这项运动里面,我们可以用数学知识解决一些实际问题.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系如图所示,图中的抛物线近似表示滑雪场地上的一座小山坡,某运动员从点O正上方50米处的A点滑出,滑出后沿一段抛物线运动.当运动员运动到离A处的水平距离为60米时,离水平线的高度为60米.
(1)求小山坡最高点到水平线的距离.
(2)求抛物线所对应的函数表达式.
(3)当运动员滑出点A后,直接写出运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为10米.
堂堂清
一、选择题(每小题4分,共32分)
1.小明在体育训练中掷出的实心球的运动路线呈如图所示的抛物线形,若实心球运动的抛物线的表达式为,其中是实心球飞行的高度,是实心球飞行的水平距离,则小明此次郑球过程中,实心球的最大高度是( )
A. B. C. D..
2.向空中发射一枚炮弹,经过秒后高度为米,且时间与高度的关系式为,若炮弹在第6秒与第14秒时的高度相等,则炮弹所在高度最高的时间是( )
A.第8秒 B.第9秒 C.第10秒 D.第11秒
3 .如图,一个移动喷灌架喷射出的水流可以近似地看成抛物线,喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度1.8米,水流喷射的最远水平距离是( )
A.20米 B.18米 C.10米 D.8米
4.有一拱桥洞呈抛物线形,这个桥洞的最大高度是16m,跨度为40m,现把它的示意图(如图)放在坐标系中,则抛物线的解析式为( )
A.y=x2+x B.y=-x2+x
C.y=-x2-x D.y=-x2+x+16
如图,某大门的形状是一抛物线形建筑,大门的地面宽8 m,在两侧距地面3.5 m高处有两个挂单位名牌匾用的铁环,两铁环的水平距离是6 m.若按图所示建立平面直角坐标系,则抛物线的解析式是( ).(建筑物厚度忽略不计)
A. B. C. D.
6.小明在期末体育测试中掷出的实心球的运动路线呈抛物线形.若实心球运动的抛物线的解析式为,其中y是实心球飞行的高度,x是实心球飞行的水平距离.已知该同学出手点A的坐标为,则实心球飞行的水平距离OB的长度为( )
A.7m B.7.5m C.8m D.8.5m
7.如图是抛物线形的拱桥,当水面宽4m时,顶点离水面2m,当水面宽度增加到6m时,水面下降( )
A.1m B.1.5m C.2.5m D.2m
8 .如图,从某建筑物10m高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直).如果抛物线的最高点M离墙1m,离地面m,则水流落地点B离墙的距离OB是( )
A.2m B.3m C.4m D.5m
二、填空题(每小题4分,共20分)
9..如图,一位篮球运动员投篮,球沿抛物线运行,然后准确落入篮筐内,已知篮筐的中心离地面的高度为,则他距篮筐中心的水平距离是 .
10 .中国羽毛球队蝉联苏迪曼杯团体赛冠军,成就了首个五连冠霸业.比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y(米)与水平距离x(米)之间满足关系,则羽毛球飞出的水平距离为 米.
11 .如图,某单位的围墙由一段段形状相同的抛物线形栅栏组成,为了牢固,每段栅栏间隔0.2米设置一根立柱(即AB间间隔0.2米的7根立柱)进行加固,若立柱EF的长为0.28米,则拱高OC为_____米
12 .如图,一次足球训练中,一球员从球门正前方将球射向球门,球射向球门的路线呈抛物线,当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米,当足球下落到离地面米时,足球飞行的水平距离为__________米.
13 .圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立平面直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点.已知雕塑OA高米,与OA水平距离5米处为水柱最高点,落水点C、D之间的距离为22米,则喷出水柱的最大高度为________米.
三、解答题(共48分)
14 .(8分)图中是抛物线形拱桥,当水面宽为4米时,拱顶距离水面2米;当水面高度下降1米时,水面宽度为多少米?
15 .(8分)如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的,正常水位时,大孔水面宽度为,顶点距水面,小孔顶点距水面.当水位上涨刚好淹没小孔时,求大孔的水面宽度.
16.(8分)如图,以一定的速度将小球沿与地面成一定角度的方向出击时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度(单位:)与飞行时间(单位:)之间具有二次函数关系.小明在一次击球过程中测得一些数据,如下表所示.
根据相关信息解答下列问题.
飞行时间 0 1 2
飞行高度 0 15 20
(1)求小球的飞行高度(单位:)关于飞行时间(单位:)的二次函数关系式;
(2)小球从飞出到落地要用多少时间?
(3)小球的飞行高度能否达到?如果能,请求出相应的飞行时间;如果不能,请说明理由.
17.(8分)如图,某城区公园有直径为7m的圆形水池,水池边安有排水槽,在中心O处修喷水装置,喷出水呈抛物线状,当水管OA高度在6m处时,距离OA水平距离1m处喷出的水流达到最大高度为8m.
(1)求抛物线解析式,并求水流落地点距离O点的距离;
(2)若不改变(1)中抛物线的形状和对称轴,若使水流落地点恰好落在圆形水池边排水槽内(不考虑边宽),则如何调节水管OA的高度?
18.(8分)某学校九年级的一场篮球比赛中,队员甲正在投篮,已知球出手时离地面高m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m.如图,设篮球运行轨迹为抛物线,篮圈距地面3m.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?
19.(8分)一隧道内设双行公路,隧道的高MN为6米.下图是隧道的截面示意图,并建立如图所示的直角坐标系,它是由一段抛物线和一个矩形CDEF的三条边围成的,矩形的长DE是8米,宽CD是2米.
(1)求该抛物线的解析式;
(2)为了保证安全,要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离.若行车道总宽度PQ(居中,两边为人行道)为6米,一辆高3.2米的货运卡车(设为长方形)靠近最右边行驶能否安全?请写出判断过程;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABHG,使H、G两点在抛物线上,A、B两点在地面DE上,设GH长为n米,“脚手架”三根木杆AG、GH、HB的长度之和为L,当n为何值时L最大,最大值为多少?
拓展培优*冲刺满分
1.如图,是某公园一圆形喷水池,在池中心竖直安装一根水管OA=1.25m,A处是喷头,水流在各个方向沿形状相同的抛物线落下,水落地后形成一个圆,圆心为O,直径为线段CB.建立如图所示的平面直角坐标系,若水流路线达到最高处时,到x轴的距离为2.25m,到y轴的距离为1m,则水落地后形成的圆的直径CB=_____m.
2 .一台自动喷灌设备的喷流情况如图所示,设水管在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线与y轴成角,水流最高点B比喷头A高2米.
(1)求抛物线解析式;
(2)求水流落地点C到O的距离;
(3)若水流的水平位移s米(抛物线上两对称点之间的距离)与水流的运动时间t之间的函数关系为,求共有几秒钟,水流的高度不低于2米?
九年级数学上分层优化堂堂清
二十二章 二次函数
22.3实际问题与二次函数
第三课时 抛物线型问题 (解析版)
学习目标:
1.能够从实际问题中抽象出二次函数模型,并运用二次函数及性质解决实际问题;
2.在探究二次函数的实际应用中学会分析问题,体会数学建模思想以及数学与生活的紧密联系性。
用二次函数解决抛物线型的一般步骤:
(1)恰当地建立直角坐标系;
(2)将已知条件转化为点的坐标;
(3)合理地设出所求函数关系式;
(4)代入已知条件或点的坐标,求出关系式;
(5)利用关系式求解问题.
二、利用二次函数解决抛物线型问题具体思路
这类问题所给的问题情境常有一个抛物线型物体,比如拱桥或隧道这些问题都可以通过构造二次承数的表达式来解决,解决这类问题般是利用数形结合思想和函数思想。
1.一般解题思路
(1)在示意图中建立适当的平面直角坐标系,将题目中所给条件转化平面直角坐标系中的坐标。
(2)根据图中坐标利用待定系数法求得二次函数的表达式。
(3)由二次函数的性质去分析解决问题,检验问题的结果是否符合实标意义,并作答。
2.卡车过拱桥(隧道)问题
在问题中,抛物线的函数表达式是首要条件,有时函数表达式已经给出,有时需要先求出来,求出函数表达式后有两种方法可以判断卡车能否从桥下通过:
(1)固定卡车的宽,看桥是否足够高(即相当于已知x的值,根据函数表达式求y的值,然后与限制的高的值比较大小);
(2)固定卡车的高,看桥是否足够宽(即相当于已知y的值,根据函数表达式求x的值,然后与限制的宽的值比较大小)
基础提升 教材核心知识点精练
知识点1:拱桥问题
【例1-1】郑州市彩虹桥新桥将于2023年9月底建成通车.新桥采用三跨连续单拱肋钢箱系杆拱桥,既保留了历史记忆,又展示出郑州的开放与创新.新桥的中跨大拱的拱肋可视为抛物线的一部分,桥面(视为水平的)与拱肋用垂直于桥面的系杆连接,测得拱肋的跨度为120米,与中点O相距30米处有一高度为27米的系杆.以所在直线为x轴,抛物线的对称轴为y轴建立如图②所示的平面直角坐标系.
(1)求抛物线的解析式;
(2)正中间系杆的长度是多少米?若相邻系杆之间的间距均为3米(不考虑系杆的粗细),是否存在一根系杆的长度恰好是长度的?请说明理由.
【答案】(1)
(2)正中间系杆的长度是36米,不存在一根系杆的长度恰好是OC长度的,理由见解析
【分析】(1)利用待定系数法求解即可;
(2)先求出正中间系杆的长度是36米,再建立方程求解即可.
【详解】(1)结合图象由题意可知:,,
设该抛物线解析式为:,
则:,
解得:,
∴.
(2)当时,,
∴正中间系杆的长度是36米.
设存在一根系杆的长度是的,即这根系杆的长度是12米,
则,
解得.
∵相邻系杆之间的间距均为3米,最中间系标在轴上,
∴每根系杆上的点的横坐标均为整数.
∴与实际不符.
∴不存在一根系杆的长度恰好是长度的.
【点评】本题考查了二次函数的实际应用,涉及到了待定系数法求函数解析式,解一元二次方程等知识,解题关键是读懂题意,找出数量关系,列出方程,并根据实际意义求解.
【例1-2】如图,有一个横截面为抛物线形状的隧道,隧道底部宽为,拱顶内高.把截面图形放在如图所示的平面直角坐标系中(原点O是的中点).
(1)求这条抛物线所对应的函数表达式;
(2)如果该隧道设计为车辆双向通行,规定车辆必须在中心黄线两侧行驶,那么一辆宽,高的大型货运卡车是否可以通过?为什么?
【答案】(1)
(2)一辆宽,高的大型货运卡车可以通过,理由见解析
【分析】(1)利用待定系数法求解即可;
(2)求出当时,x的值,再根据车辆宽且只能在中心的两侧行驶进行求解即可.
【详解】(1)解:由题意得,点C的坐标为,点A和点B的坐标分别为,
设抛物线解析式为,
把代入得,解得,
∴抛物线解析式为;
(2)解:一辆宽,高的大型货运卡车可以通过,理由如下:
在中,当时,解得,
∵,
∴,
∴一辆宽,高的大型货运卡车可以通过.
【点评】本题主要考查了二次函数的实际应用,正确求出对应的函数解析式是解题的关键.
知识点2:投球问题
【例2-1】掷实心球是中考体育考试项目之一.如图1是一名男生掷实心球情境,实心球行进路线是一条抛物线,行进高度与水平距离之间的函数关系如图2所示.掷出时,起点处高度为.当水平距离为时,实心球行进至最高点处.
(1)求y关于x的函数表达式;
(2)根据中考体育考试评分标准(男生版),投掷过程中,实心球从起点到落地点的水平距离大于等于时,即可得满分10分.该男生在此项考试中能否得满分,请说明理由.
【答案】(1)
(2)不能;理由见解析
【分析】(1)由图2可知,顶点坐标为,设二次函数表达式为,由此即可求解;
(2)令(1)中抛物线的解析式,且,解方程,即可求解.
【详解】(1)解:根据题意设关于的函数表达式为,
把代入解析式得,,
解得,,
∴关于的函数表达式为:,
即:.
(2)解:不能得满分,理由如下,
根据题意,令,且,
∴,
解方程得,,(舍去),
∵,
∴不能得满分.
【点评】本题主要考查二次函数的实际运用,掌握二次函数的性质及求解是解题的关键.
【例2-2】实心球是中考体育项目之一.在掷实心球时,实心球被掷出后的运动路线可以看作是抛物线的一部分,已知小军在一次掷实心球训练中,第一次投掷时出手点距地面1.8m,实心球运动至最高点时距地面3.4m,距出手点的水平距离为4m.设实心球掷出后距地面的竖直高度为y(m),实心球距出手点的水平距离为x(m).如图,以水平方向为x轴,出手点所在竖直方向为y轴建立平面直角坐标系.
(1)求第一次掷实心球时运动路线所在抛物线的表达式.
(2)若实心球投掷成绩(即出手点与着陆点的水平距离)达到12.4m为满分,请判断小军第一次投掷实心球能否得满分.
(3)第二次投掷时,实心球运动的竖直高度y与水平距离x近似满足函数关系.记小军第一次投掷时出手点与着陆点的水平距离为,第二次投掷时出手点与着陆点的水平距离为,则______(填“>”“<”“=”).
【答案】(1)
(2)不能得满分
(3)<
【分析】(1)设抛物线的表达式为,将代入解得a即可;
(2)令,解得x,与12.4m比较即可;
(3)令,解得x,根据(2)所得即可比较与.
【详解】(1)由题意,可知抛物线最高点的坐标为,
设抛物线的表达式为,
将代入,得,
解得.
∴第一次掷实心球时运动路线所在抛物线的表达式为;
(2)令,解得(负值已舍去),
∴实心球出手点与着陆点的水平距离为m.
∵,即,∴,
∴小军第一次投掷实心球不能得满分.
(3)∵,
解得(负值已舍去),
,,
,,
∴.
故答案为:<.
【点评】本题考查二次函数的应用以及待定系数法求解析式,熟练掌握二次函数的性质是解题的关键.
知识点3:喷水问题
【例3-1】一名运动员在高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面的高度与离起跳点A的水平距离之间的函数关系如图所示,运动员离起跳点A的水平距离为时达到最高点,当运动员离起跳点A的水平距离为时离水面的距离为.
(1)求y关于x的函数表达式;
(2)求运动员从起跳点到入水点的水平距离的长.
【答案】(1)y关于x的函数表达式为;
(2)运动员从起跳点到入水点的水平距离的长为.
【分析】(1)由题意得抛物线的对称轴为,经过点,,利用待定系数法即可求解;
(2)令,解方程即可求解.
【详解】(1)解:由题意得抛物线的对称轴为,经过点,,
设抛物线的表达式为,
∴,解得,
∴y关于x的函数表达式为;
(2)解:令,则,
解得(负值舍去),
∴运动员从起跳点到入水点的水平距离的长为.
【点睛】本题考查了二次函数在实际问题中的应用,数形结合并熟练掌握运用待定系数法求抛物线的解析式是解题的关键.
【例3-2】如图①,有一移动灌溉装置喷出水柱的路径可近似地看作一条抛物线,该灌溉装置的喷水头到水平地面的距离为1米,喷出的抛物线形水柱对称轴为直线.用该灌溉装置灌溉一坡地草坪,其水柱的高度y(单位:米)与水柱落地处距离喷水头的距离x(单位:米)之间的函数关系式为,其图像如图②所示.已知坡地所在直线经过点.
(1)的值为______;
(2)若,求水柱与坡面之间的最大铅直高度;
(3)若点B横坐标为18,水柱能超过点B,则a的取值范围为______;
(4)若时,到喷水头水平距离为16米的A处有一棵新种的银杏树需要被灌溉,园艺工人将灌溉装置水平向后移动4米,试判断灌溉装置能否灌溉到这棵树,并说明理由.
【答案】(1)1
(2)水柱与坡面之间的最大铅直高度为米
(3)
(4)水平向后移动4米,不能灌溉到这棵树,理由见解析
【分析】(1)代入抛物线与y轴的交点的坐标即可求解;
(2)根据已知条件求出抛物线解析式及直线解析式,设抛物线上一点P点横坐标为t,作作轴交于点Q,用t表示P点和Q点的坐标,并计算的长度,建立关于t的二次函数,在取值范围内求最大值即可;
(3)代入B点横坐标到一次函数解析式,求出对应纵坐标;代入点、抛物线对称轴及B点横坐标到二次函数解析式,建立不等式进行求解;
(4)根据平移求得平移后的抛物线解析式,代入到抛物线解析式和直线解析式进行对比即可.
【详解】(1)代入到抛物线解析式,得:;
故答案为:1;
(2)设抛物线的解析式为
将点代入,得
抛物线的解析式为
即
坡地经过点
的解析式为
如解图,
设抛物线上一点,过点P作轴交于点Q,
则,的长为
,
函数图像开口向下,d有最大值
根据顶点公式当时,有最大值
水柱与坡面之间的最大铅直高度为米;
故答案为:水柱与坡面之间的最大铅直高度为米;
(3)由(2)知,直线的解析式为,
时,
,
抛物线的解析式为,即,
当时,,要使水柱能超过点B则,
解得
故答案为:;
(4)不能;
当灌溉装置水平向后移动4米时,由(2)可得平移后的抛物线解析式为.
将代入抛物线解析式,得,
将代入直线OB解析式,得
水平向后移动4米,不能灌溉到这棵树.
【点评】本题考查二次函数的实际应用,掌握待定系数法求解二次函数解析式和直线解析式、平移规律求二次函数解析式、根据坐标关系及二次函数求线段最大值是解题的关键.
能力强化 能力强化训练
1.一隧道内设双行公路,隧道的高MN为6米.下图是隧道的截面示意图,并建立如图所示的直角坐标系,它是由一段抛物线和一个矩形CDEF的三条边围成的,矩形的长DE是8米,宽CD是2米.
(1)求该抛物线的解析式;
(2)为了保证安全,要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离.若行车道总宽度PQ(居中,两边为人行道)为6米,一辆高3.2米的货运卡车(设为长方形)靠近最右边行驶能否安全?请写出判断过程;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABHG,使H、G两点在抛物线上,A、B两点在地面DE上,设GH长为n米,“脚手架”三根木杆AG、GH、HB的长度之和为L,当n为何值时L最大,最大值为多少?
【答案】(1)y=-x2+4;(2)能安全通过,见解析;(3)n=4时,L有最大值,最大值为14
【分析】(1)根据题意和函数图象,可以设出抛物线的解析式,然后根据抛物线过点F和点M即可求得该抛物线的解析式;
(2)先求出抛物线的解析式,再根据题意判断该隧道能通过的车辆的最高高度,便可判断该车辆能安全通过.
(3)射出H的坐标,用n表示出L,利用二次函数的性质求解即可.
【详解】解:(1)由题意得M(0,4),F(4,0)
可设抛物线的解析式为y=ax2+4,
将F(4,0)代入y=ax2+4中,得a=-,
∴抛物线的解析式为y=-x2+4;
(2)当x=3,y=,
+2-=3.253.2,∴能安全通过;
(3)由GH=n,可设H(),
∴GH+GA+BH=n+()×2+2×2=,
∴L=,
∵a<0,抛物线开口向下,
∴当n=-=4时,L有最大值,最大值为14.
【点评本题考查了二次函数的实际应用,解题的关键是要注意自变量的取值范围必须使实际问题有意义.
2.北方的冬天,人们酷爱冰雪运动,在这项运动里面,我们可以用数学知识解决一些实际问题.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系如图所示,图中的抛物线近似表示滑雪场地上的一座小山坡,某运动员从点O正上方50米处的A点滑出,滑出后沿一段抛物线运动.当运动员运动到离A处的水平距离为60米时,离水平线的高度为60米.
(1)求小山坡最高点到水平线的距离.
(2)求抛物线所对应的函数表达式.
(3)当运动员滑出点A后,直接写出运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为10米.
【答案】(1)40米
(2)
(3)运动员运动的水平距离为为米时,运动员与小山坡的竖直距离为10米
【分析】(1)由抛物线的解析式得出最大值即可;
(2)把、代入可得抛物线所对应的函数表达式;
(3)根据纵坐标的差为10,列出方程可得答案.
【详解】(1)解:由,得
当时,y有最大值为40.
∴小山坡最高点到水平线的距离为40米.
(2)解:把、代入中,得
得解得
∴抛物线所对应的函数表达式.
(3)解:设运动员运动的水平距离是x米,
此时小山坡的高度是,
运动员运动的水平高度是,
∴,
解得或0(舍去),
答:运动员运动的水平距离为米时,运动员与小山坡的竖直距离为10米.
【点评】本题考查二次函数的基本性质及其应用,熟练掌握二次函数的基本性质,并能将实际问题与二次函数模型相结合是解决本题的关键.
堂堂清
一、选择题(每小题4分,共32分)
1.小明在体育训练中掷出的实心球的运动路线呈如图所示的抛物线形,若实心球运动的抛物线的表达式为,其中是实心球飞行的高度,是实心球飞行的水平距离,则小明此次郑球过程中,实心球的最大高度是( )
A. B. C. D.
【答案】B
【分析】由可得抛物线的顶点坐标为:,结合函数的性质可得答案.
【详解】解:∵,
∴抛物线的顶点坐标为:,
∵,
∴实心球的最大高度是,
故选B.
【点评】本题考查的是抛物线的图像与性质,掌握“利用顶点式求解抛物线的顶点坐标或函数的最值”是解本题的关键.
2.向空中发射一枚炮弹,经过秒后高度为米,且时间与高度的关系式为,若炮弹在第6秒与第14秒时的高度相等,则炮弹所在高度最高的时间是( )
A.第8秒 B.第9秒 C.第10秒 D.第11秒
【答案】C
【分析】本题先根据题意求出抛物线的对称轴,即可得出顶点的横坐标,从而得出跑弹所在高度最高时的值.
【详解】解:∵此炮弹在第6与第14秒时的高度相等,
∴抛物线的对称轴是直线,
∴炮弹所在高度最高是10秒,
故选:C.
【点评】本题主要考查了二次函数的应用,在解题时要能根据题意求出抛物线的对称轴得出答案是本题的关键.
3 .如图,一个移动喷灌架喷射出的水流可以近似地看成抛物线,喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度1.8米,水流喷射的最远水平距离是( )
A.20米 B.18米 C.10米 D.8米
【答案】A
【分析】根据顶点式求得抛物线解析式,进而求得与轴的交点坐标即可求解.
【详解】解:∵喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度1.8米,
设抛物线解析式为,将点代入,得
解得
∴抛物线解析式为
令,解得(负值舍去)
即,
故选:A
【点评】本题考查了二次函数的实际应用,根据题意求得解析式是解题的关键.
4.有一拱桥洞呈抛物线形,这个桥洞的最大高度是16m,跨度为40m,现把它的示意图(如图)放在坐标系中,则抛物线的解析式为( )
A.y=x2+x B.y=-x2+x
C.y=-x2-x D.y=-x2+x+16
【答案】B
【分析】根据题意设出顶点式,将原点代入即可解题.
【详解】解:由图可知,该抛物线开口向下,对称轴为x=20,
最高点坐标为(20,16),且经过原点,
由此可设该抛物线解析式为,
将原点坐标代入可得,
解得:,
故该抛物线解析式为
故选:B.
【点评】本题主要考查二次函数图像性质的实际应用、二次函数顶点式等,找到顶点坐标设出顶点式是解题关键.
如图,某大门的形状是一抛物线形建筑,大门的地面宽8 m,在两侧距地面3.5 m高处有两个挂单位名牌匾用的铁环,两铁环的水平距离是6 m.若按图所示建立平面直角坐标系,则抛物线的解析式是( ).(建筑物厚度忽略不计)
A. B. C. D.
【答案】A
【分析】先根据函数图象可得抛物线与轴的两个交点坐标为和,再设抛物线的解析式为,将点代入即可得.
【详解】解:由函数图象可知,抛物线与轴的两个交点坐标为和,且经过点,
设抛物线的解析式为,
将点代入得:,
解得,
则抛物线的解析式为,即为,
故选:A.
【点评】本题考查了求抛物线的解析式,熟练掌握待定系数法是解题关键.
6.小明在期末体育测试中掷出的实心球的运动路线呈抛物线形.若实心球运动的抛物线的解析式为,其中y是实心球飞行的高度,x是实心球飞行的水平距离.已知该同学出手点A的坐标为,则实心球飞行的水平距离OB的长度为( )
A.7m B.7.5m C.8m D.8.5m
【答案】C
【分析】根据题意待定系数法求解析式,再令,即可求解.
【详解】解:∵实心球运动的抛物线的解析式为,点A的坐标为,
∴,
解得,
,
令,,
即,
解得(舍去),
故选:C.
【点评】本题考查了二次函数的应用,待定系数法求解析式,求二次函数与坐标轴的交点,掌握二次函数的性质是解题的关键.
7.如图是抛物线形的拱桥,当水面宽4m时,顶点离水面2m,当水面宽度增加到6m时,水面下降( )
A.1m B.1.5m C.2.5m D.2m
【答案】C
【分析】根据已知得出直角坐标系,进而求出二次函数的解析式,再把代入抛物线的解析式得出水面宽度,即可得出答案.
【详解】解:建立平面直角坐标系,设横轴通过,纵轴通过中点且通过顶点,则通过画图可得知为原点,
由平面直角坐标系可知,,即,
设抛物线的解析式为,
将点代入得:,解得,
则抛物线的解析式为,即,
当时,,
所以水面下降,
故选:C.
【点评】本题主要考查了二次函数的应用,根据已知建立平面直角坐标系从而得出二次函数的解析式是解决问题的关键.
8 .如图,从某建筑物10m高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直).如果抛物线的最高点M离墙1m,离地面m,则水流落地点B离墙的距离OB是( )
A.2m B.3m C.4m D.5m
【解答】解:设抛物线的解析式为y=a(x﹣1)2+,由题意,得
10=a+,
a=﹣.
∴抛物线的解析式为:y=﹣(x﹣1)2+.
当y=0时,
0=﹣(x﹣1)2+,
解得:x1=﹣1(舍去),x2=3.
OB=3m.
故选:B.
二、填空题(每小题4分,共20分)
9..如图,一位篮球运动员投篮,球沿抛物线运行,然后准确落入篮筐内,已知篮筐的中心离地面的高度为,则他距篮筐中心的水平距离是 .
【答案】4
【分析】将代入中可求出x,结合图形可知,即可求出OH.
【详解】解:当时,,解得:或,
结合图形可知:,
故答案为:4
【点评】本题考查二次函数的实际应用:投球问题,解题的关键是结合函数图形确定x的值.
10 .中国羽毛球队蝉联苏迪曼杯团体赛冠军,成就了首个五连冠霸业.比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y(米)与水平距离x(米)之间满足关系,则羽毛球飞出的水平距离为 米.
【答案】5
【分析】试题分析:根据羽毛球飞出的水平距离即为抛物线与x轴正半轴交点到原点的距离求出即可.
【详解】当y=0时,,
解得:x1=﹣1(舍),x2=5.
∴羽毛球飞出的水平距离为5米.
11 .如图,某单位的围墙由一段段形状相同的抛物线形栅栏组成,为了牢固,每段栅栏间隔0.2米设置一根立柱(即AB间间隔0.2米的7根立柱)进行加固,若立柱EF的长为0.28米,则拱高OC为_____米
【答案】0.64
【分析】根据抛物线,建立直角坐标系,求出抛物线解析式,即可求得OC的长.
【详解】
解:如图,以点C为坐标系原点,OC所在直线为y轴,建立直角坐标系.
设抛物线的解析式为,
由题意可知:点A的横坐标为-0.8,点F的横坐标为-0.6,
代入,
有,,
点A的纵坐标即为OC的长,
∴0.36a+0.28=0.64a,
解得a=1,
∴抛物线解析式为,
,
故OC的长为:0.64m.
【点评】本题考查根据抛物线构建直角坐标系,解决实际问题,熟练掌握二次函数相关知识点是解题的关键.
12 .如图,一次足球训练中,一球员从球门正前方将球射向球门,球射向球门的路线呈抛物线,当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米,当足球下落到离地面米时,足球飞行的水平距离为__________米.
【答案】10
【分析】设抛物线的解析式为,代入原点,确定解析式为,当y=米时,求得x的值即可.
【详解】设抛物线的解析式为,代入原点,得:
,
解得a=,
∴抛物线的解析式为,
当y=米时,
,
解得x=10,x=2(舍去),
足球飞行的水平距离为10米,
故答案为:10.
【点评】本题考查了抛物线的解析式,已知函数值求自变量值,熟练掌握待定系数法是解题的关键.
13 .圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立平面直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点.已知雕塑OA高米,与OA水平距离5米处为水柱最高点,落水点C、D之间的距离为22米,则喷出水柱的最大高度为________米.
【答案】6
【分析】设水柱所在抛物线的函数表达式为 (x≥0),根据题意得到A(0,),D(11,0),对称轴x=5,用待定系数法求出函数表达式,把x=5代入,即可得到喷出水柱的最大高度.
【详解】解:设水柱所在抛物线的函数表达式为 (x≥0),
∵雕塑OA高米,
∴点A的坐标是(0,),
∵落水点C、D之间的距离为22米,
∴点D的坐标为(11,0),
∵与OA水平距离5米处为水柱最高点,
∴抛物线的对称轴为x=5,
得到
解得
∴水柱所在抛物线的函数表达式为 (x≥0)
当x=5时,,
∴ 喷出水柱的最大高度为6米,
故答案为:6
【点评】本题考查了二次函数的实际应用,待定系数法求出函数表达式是基础,求出函数的最大值是关键。
三、解答题(共48分)
14 .(8分)图中是抛物线形拱桥,当水面宽为4米时,拱顶距离水面2米;当水面高度下降1米时,水面宽度为多少米?
【答案】
【分析】根据已知得出直角坐标系,进而求出二次函数解析式,再根据通过把y=-1代入抛物线解析式得出水面宽度,即可得出答案.
【详解】解:建立平面直角坐标系.设二次函数的解析式为(a≠0).
∵图象经过点(2,-2),
∴-2=4a,
解得:.
∴.
当y=-3时,.
答:当水面高度下降1米时,水面宽度为米.
【点睛】此题主要考查了二次函数的应用,根据已知建立坐标系从而得出二次函数解析式是解决问题的关键,难度一般.
15 .(8分)如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的,正常水位时,大孔水面宽度为,顶点距水面,小孔顶点距水面.当水位上涨刚好淹没小孔时,求大孔的水面宽度.
【答案】此时大孔的水面宽度为10m.
【分析】根据题意,建立如图所示的平面直角坐标系,可以得到A、B、M的坐标,设出函数关系式,待定系数求解函数式.根据NC的长度,得出函数值y,代入解析式,即可得出E、F的坐标,进而得出答案.
【详解】解:如图,建立如图所示的平面直角坐标系,由题意得,M点坐标为(0,6),A点坐标为(-10,0),B点坐标为(10,0),
设中间大抛物线的函数式为y=ax2+6,
∵点B在此抛物线上,
∴0=a×102+6,
解得a=-,
∴函数式为y=-x2+6.
∵NC=4.5m,
∴令y=4.5,
代入解析式得-x2+6=4.5,
x1=5,x2=-5,
∴可得EF=5-(-5)=10.
此时大孔的水面宽度为10m.
【点评】本题是二次函数的实际应用,考查了待定系数法求二次函数的解析式,由函数值求自变量的值,解答时求出函数的解析式是关键.
16.(8分)如图,以一定的速度将小球沿与地面成一定角度的方向出击时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度(单位:)与飞行时间(单位:)之间具有二次函数关系.小明在一次击球过程中测得一些数据,如下表所示.
根据相关信息解答下列问题.
飞行时间 0 1 2
飞行高度 0 15 20
(1)求小球的飞行高度(单位:)关于飞行时间(单位:)的二次函数关系式;
(2)小球从飞出到落地要用多少时间?
(3)小球的飞行高度能否达到?如果能,请求出相应的飞行时间;如果不能,请说明理由.
【答案】(1)
(2)
(3)不能,理由见解析
【分析】(1)利用待定系数法即可求解;
(2)令h=0即可求解;
(3)令,得到方程无解即可判断.
(1)
由题意可设关于的二次函数关系式为,
因为当,2时,,20,
∴,
解得:.
∴关于的二次函数关系式为.
(2)
当,,解得:,.
∴小球从飞出到落地所用的时间为.
(3)
小球的飞行高度不能达到.
理由如下:
当时,,方程即为,
∵,
∴此方程无实数根.
即小球飞行的高度不能达到.
【点评】此题主要考查一元二次方程与二次函数的实际应用,解题的关键是根据题意求出函数解析式,再根据题意进行解答.
17.(8分)如图,某城区公园有直径为7m的圆形水池,水池边安有排水槽,在中心O处修喷水装置,喷出水呈抛物线状,当水管OA高度在6m处时,距离OA水平距离1m处喷出的水流达到最大高度为8m.
(1)求抛物线解析式,并求水流落地点距离O点的距离;
(2)若不改变(1)中抛物线的形状和对称轴,若使水流落地点恰好落在圆形水池边排水槽内(不考虑边宽),则如何调节水管OA的高度?
【解答】解:(1)∵抛物线的顶点为(1,8),
∴设抛物线的解析式为y=a(x﹣1)2+8,
把A(0,6)代入可得a=﹣2,
∴解析式为y=﹣2(x﹣1)2+8,
当y=0时,x=3或﹣1(舍去),
答:解析式为y=﹣2(x﹣1)2+8,水流落地点距离O点的距离是3米;
(2)抛物线的表达式为y=﹣2(x﹣1)2+k,
把(3.5,0)代入可得k=12.5,
∴解析式为y=﹣2(x﹣1)2+12.5,
当x=0时,y=10.5,
答:水管OA的高度调整为10.5米.
18.(8分)某学校九年级的一场篮球比赛中,队员甲正在投篮,已知球出手时离地面高m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m.如图,设篮球运行轨迹为抛物线,篮圈距地面3m.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?
【答案】(1)能准确投中,理由见解析
(2)乙能盖帽拦截成功,理由见解析
【分析】(1)根据抛物线的顶点坐标及球出手时的坐标,由待定系数法可确定抛物线的解析式,令,求出y的值,与3m比较即可作出判断;
(2)将代入,进而得出答案.
【详解】(1)解:球出手点、最高点、篮圈坐标分别为,
设这条抛物线对应的函数解析式为,
将点代入,可得,解得,
∴,
当时,,
∴此球能准确投中;
(2)当时,,
∴乙能盖帽拦截成功.
【点睛】本题主要考查了二次函数实际应用,根据题意求得函数解析式,掌握二次函数的性质是解题的关键.
19.(8分)一隧道内设双行公路,隧道的高MN为6米.下图是隧道的截面示意图,并建立如图所示的直角坐标系,它是由一段抛物线和一个矩形CDEF的三条边围成的,矩形的长DE是8米,宽CD是2米.
(1)求该抛物线的解析式;
(2)为了保证安全,要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离.若行车道总宽度PQ(居中,两边为人行道)为6米,一辆高3.2米的货运卡车(设为长方形)靠近最右边行驶能否安全?请写出判断过程;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABHG,使H、G两点在抛物线上,A、B两点在地面DE上,设GH长为n米,“脚手架”三根木杆AG、GH、HB的长度之和为L,当n为何值时L最大,最大值为多少?
【答案】(1)y=-x2+4;(2)能安全通过,见解析;(3)n=4时,L有最大值,最大值为14
【分析】(1)根据题意和函数图象,可以设出抛物线的解析式,然后根据抛物线过点F和点M即可求得该抛物线的解析式;
(2)先求出抛物线的解析式,再根据题意判断该隧道能通过的车辆的最高高度,便可判断该车辆能安全通过.
(3)射出H的坐标,用n表示出L,利用二次函数的性质求解即可.
【详解】解:(1)由题意得M(0,4),F(4,0)
可设抛物线的解析式为y=ax2+4,
将F(4,0)代入y=ax2+4中,得a=-,
∴抛物线的解析式为y=-x2+4;
(2)当x=3,y=,
+2-=3.253.2,∴能安全通过;
(3)由GH=n,可设H(),
∴GH+GA+BH=n+()×2+2×2=,
∴L=,
∵a<0,抛物线开口向下,
∴当n=-=4时,L有最大值,最大值为14.
【点睛】本题考查了二次函数的实际应用,解题的关键是要注意自变量的取值范围必须使实际问题有意义.
拓展培优*冲刺满分
1.如图,是某公园一圆形喷水池,在池中心竖直安装一根水管OA=1.25m,A处是喷头,水流在各个方向沿形状相同的抛物线落下,水落地后形成一个圆,圆心为O,直径为线段CB.建立如图所示的平面直角坐标系,若水流路线达到最高处时,到x轴的距离为2.25m,到y轴的距离为1m,则水落地后形成的圆的直径CB=_____m.
【答案】5
【分析】设y轴右侧的抛物线解析式为:y=a(x 1)2+2.25,将A(0,1.25)代入,求得a,从而可得抛物线的解析式,再令函数值为0,解方程可得点B坐标,从而可得CB的长.
【详解】解:设y轴右侧的抛物线解析式为:y=a(x﹣1)2+2.25
∵点A(0,1.25)在抛物线上
∴1.25=a(0﹣1)2+2.25
解得:a=﹣1
∴抛物线的解析式为:y=﹣(x﹣1)2+2.25
令y=0得:0=﹣(x﹣1)2+2.25
解得:x=2.5或x=﹣0.5(舍去)
∴点B坐标为(﹣2.5,0)
∴OB=OC=2.5
∴CB=5
故答案为:5.
【点评】本题考查了二次函数在实际问题中的应用,明确二次函数的相关性质及正确的解方程,是解题的关键.
2 .一台自动喷灌设备的喷流情况如图所示,设水管在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线与y轴成角,水流最高点B比喷头A高2米.
(1)求抛物线解析式;
(2)求水流落地点C到O的距离;
(3)若水流的水平位移s米(抛物线上两对称点之间的距离)与水流的运动时间t之间的函数关系为,求共有几秒钟,水流的高度不低于2米?
【答案】(1)y= 0.5(x 2)2+3.5;(2)2+;(3)
【分析】(1)作BD⊥y轴于点D,由∠DAB=45°,就可以求出AD=BD=2,就可以求出B的坐标,设抛物线的解析式为y=a(x 2)2+3.5,由待定系数法求出其解即可;
(2)当y=0时代入(1)的解析式求出其解即可;
(3)当y=2时代入(1)的解析式求出s的值,再将s的值代入t=0.8s求出t的值即可.
【详解】解:(1)作BD⊥y轴于点D,
∴∠ADB=90°.
∵∠DAB=45°,
∴∠ABD=∠DBA=45°,
∴AD=BD=2,
∵OA=1.5,
∴B(2,3.5),A(0,1.5).
设抛物线的解析式为y=a(x 2)2+3.5,由题意,得
1.5=4a+3.5,
解得:a= 0.5.
∴y= 0.5(x 2)2+3.5.
答:抛物线解析式为y= 0.5(x 2)2+3.5;
(2)当y=0时,
0= 0.5(x 2)2+3.5.
解得:x1=2+,x2=2 (舍去),
∴水流落地点C到O点的距离为2+;
(3)当y=2时,
2= 0.5(x 2)2+3.5.
解得:x3=2+,x4=2 ,
∴水流位移的距离为:2+ (2 )=2,
∴t=0.8×2=,
∴共有秒钟,水流高度不低于2米.
【点评】本题考查了待定系数法求二次函数的解析式的运用,顶点式的运用,由函数值求自变量的值的运用,解答时求出二次函数的解析式是关键.
老师对你说:
老师对你说:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学上分层优化堂堂清
二十二章 二次函数
22.3实际问题与二次函数
第三课时 抛物线型问题
学习目标:
1.能够从实际问题中抽象出二次函数模型,并运用二次函数及性质解决实际问题;
2.在探究二次函数的实际应用中学会分析问题,体会数学建模思想以及数学与生活的紧密联系性。
用二次函数解决抛物线型的一般步骤:
(1)恰当地建立直角坐标系;
(2)将已知条件转化为点的坐标;
(3)合理地设出所求函数关系式;
(4)代入已知条件或点的坐标,求出关系式;
(5)利用关系式求解问题.
二、利用二次函数解决抛物线型问题具体思路
这类问题所给的问题情境常有一个抛物线型物体,比如拱桥或隧道这些问题都可以通过构造二次承数的表达式来解决,解决这类问题般是利用数形结合思想和函数思想。
1.一般解题思路
(1)在示意图中建立适当的平面直角坐标系,将题目中所给条件转化平面直角坐标系中的坐标。
(2)根据图中坐标利用待定系数法求得二次函数的表达式。
(3)由二次函数的性质去分析解决问题,检验问题的结果是否符合实标意义,并作答。
2.卡车过拱桥(隧道)问题
在问题中,抛物线的函数表达式是首要条件,有时函数表达式已经给出,有时需要先求出来,求出函数表达式后有两种方法可以判断卡车能否从桥下通过:
(1)固定卡车的宽,看桥是否足够高(即相当于已知x的值,根据函数表达式求y的值,然后与限制的高的值比较大小);
(2)固定卡车的高,看桥是否足够宽(即相当于已知y的值,根据函数表达式求x的值,然后与限制的宽的值比较大小)
基础提升 教材核心知识点精练
知识点1:拱桥问题
【例1-1】郑州市彩虹桥新桥将于2023年9月底建成通车.新桥采用三跨连续单拱肋钢箱系杆拱桥,既保留了历史记忆,又展示出郑州的开放与创新.新桥的中跨大拱的拱肋可视为抛物线的一部分,桥面(视为水平的)与拱肋用垂直于桥面的系杆连接,测得拱肋的跨度为120米,与中点O相距30米处有一高度为27米的系杆.以所在直线为x轴,抛物线的对称轴为y轴建立如图②所示的平面直角坐标系.
(1)求抛物线的解析式;
(2)正中间系杆的长度是多少米?若相邻系杆之间的间距均为3米(不考虑系杆的粗细),是否存在一根系杆的长度恰好是长度的?请说明理由.
【例1-2】如图,有一个横截面为抛物线形状的隧道,隧道底部宽为,拱顶内高.把截面图形放在如图所示的平面直角坐标系中(原点O是的中点).
(1)求这条抛物线所对应的函数表达式;
(2)如果该隧道设计为车辆双向通行,规定车辆必须在中心黄线两侧行驶,那么一辆宽,高的大型货运卡车是否可以通过?为什么?
知识点2:投球问题
【例2-1】掷实心球是中考体育考试项目之一.如图1是一名男生掷实心球情境,实心球行进路线是一条抛物线,行进高度与水平距离之间的函数关系如图2所示.掷出时,起点处高度为.当水平距离为时,实心球行进至最高点处.
(1)求y关于x的函数表达式;
(2)根据中考体育考试评分标准(男生版),投掷过程中,实心球从起点到落地点的水平距离大于等于时,即可得满分10分.该男生在此项考试中能否得满分,请说明理由.
【例2-2】实心球是中考体育项目之一.在掷实心球时,实心球被掷出后的运动路线可以看作是抛物线的一部分,已知小军在一次掷实心球训练中,第一次投掷时出手点距地面1.8m,实心球运动至最高点时距地面3.4m,距出手点的水平距离为4m.设实心球掷出后距地面的竖直高度为y(m),实心球距出手点的水平距离为x(m).如图,以水平方向为x轴,出手点所在竖直方向为y轴建立平面直角坐标系.
(1)求第一次掷实心球时运动路线所在抛物线的表达式.
(2)若实心球投掷成绩(即出手点与着陆点的水平距离)达到12.4m为满分,请判断小军第一次投掷实心球能否得满分.
(3)第二次投掷时,实心球运动的竖直高度y与水平距离x近似满足函数关系.记小军第一次投掷时出手点与着陆点的水平距离为,第二次投掷时出手点与着陆点的水平距离为,则______(填“>”“<”“=”).
知识点3:喷水问题
【例3-1】一名运动员在高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面的高度与离起跳点A的水平距离之间的函数关系如图所示,运动员离起跳点A的水平距离为时达到最高点,当运动员离起跳点A的水平距离为时离水面的距离为.
(1)求y关于x的函数表达式;
(2)求运动员从起跳点到入水点的水平距离的长.
【例3-2】如图①,有一移动灌溉装置喷出水柱的路径可近似地看作一条抛物线,该灌溉装置的喷水头到水平地面的距离为1米,喷出的抛物线形水柱对称轴为直线.用该灌溉装置灌溉一坡地草坪,其水柱的高度y(单位:米)与水柱落地处距离喷水头的距离x(单位:米)之间的函数关系式为,其图像如图②所示.已知坡地所在直线经过点.
(1)的值为______;
(2)若,求水柱与坡面之间的最大铅直高度;
(3)若点B横坐标为18,水柱能超过点B,则a的取值范围为______;
(4)若时,到喷水头水平距离为16米的A处有一棵新种的银杏树需要被灌溉,园艺工人将灌溉装置水平向后移动4米,试判断灌溉装置能否灌溉到这棵树,并说明理由.
能力强化 能力强化训练
1.一隧道内设双行公路,隧道的高MN为6米.下图是隧道的截面示意图,并建立如图所示的直角坐标系,它是由一段抛物线和一个矩形CDEF的三条边围成的,矩形的长DE是8米,宽CD是2米.
(1)求该抛物线的解析式;
(2)为了保证安全,要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离.若行车道总宽度PQ(居中,两边为人行道)为6米,一辆高3.2米的货运卡车(设为长方形)靠近最右边行驶能否安全?请写出判断过程;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABHG,使H、G两点在抛物线上,A、B两点在地面DE上,设GH长为n米,“脚手架”三根木杆AG、GH、HB的长度之和为L,当n为何值时L最大,最大值为多少?
2.北方的冬天,人们酷爱冰雪运动,在这项运动里面,我们可以用数学知识解决一些实际问题.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系如图所示,图中的抛物线近似表示滑雪场地上的一座小山坡,某运动员从点O正上方50米处的A点滑出,滑出后沿一段抛物线运动.当运动员运动到离A处的水平距离为60米时,离水平线的高度为60米.
(1)求小山坡最高点到水平线的距离.
(2)求抛物线所对应的函数表达式.
(3)当运动员滑出点A后,直接写出运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为10米.
堂堂清
一、选择题(每小题4分,共32分)
1.小明在体育训练中掷出的实心球的运动路线呈如图所示的抛物线形,若实心球运动的抛物线的表达式为,其中是实心球飞行的高度,是实心球飞行的水平距离,则小明此次郑球过程中,实心球的最大高度是( )
A. B. C. D..
2.向空中发射一枚炮弹,经过秒后高度为米,且时间与高度的关系式为,若炮弹在第6秒与第14秒时的高度相等,则炮弹所在高度最高的时间是( )
A.第8秒 B.第9秒 C.第10秒 D.第11秒
3 .如图,一个移动喷灌架喷射出的水流可以近似地看成抛物线,喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度1.8米,水流喷射的最远水平距离是( )
A.20米 B.18米 C.10米 D.8米
4.有一拱桥洞呈抛物线形,这个桥洞的最大高度是16m,跨度为40m,现把它的示意图(如图)放在坐标系中,则抛物线的解析式为( )
A.y=x2+x B.y=-x2+x
C.y=-x2-x D.y=-x2+x+16
如图,某大门的形状是一抛物线形建筑,大门的地面宽8 m,在两侧距地面3.5 m高处有两个挂单位名牌匾用的铁环,两铁环的水平距离是6 m.若按图所示建立平面直角坐标系,则抛物线的解析式是( ).(建筑物厚度忽略不计)
A. B. C. D.
6.小明在期末体育测试中掷出的实心球的运动路线呈抛物线形.若实心球运动的抛物线的解析式为,其中y是实心球飞行的高度,x是实心球飞行的水平距离.已知该同学出手点A的坐标为,则实心球飞行的水平距离OB的长度为( )
A.7m B.7.5m C.8m D.8.5m
7.如图是抛物线形的拱桥,当水面宽4m时,顶点离水面2m,当水面宽度增加到6m时,水面下降( )
A.1m B.1.5m C.2.5m D.2m
8 .如图,从某建筑物10m高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直).如果抛物线的最高点M离墙1m,离地面m,则水流落地点B离墙的距离OB是( )
A.2m B.3m C.4m D.5m
二、填空题(每小题4分,共20分)
9..如图,一位篮球运动员投篮,球沿抛物线运行,然后准确落入篮筐内,已知篮筐的中心离地面的高度为,则他距篮筐中心的水平距离是 .
10 .中国羽毛球队蝉联苏迪曼杯团体赛冠军,成就了首个五连冠霸业.比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y(米)与水平距离x(米)之间满足关系,则羽毛球飞出的水平距离为 米.
11 .如图,某单位的围墙由一段段形状相同的抛物线形栅栏组成,为了牢固,每段栅栏间隔0.2米设置一根立柱(即AB间间隔0.2米的7根立柱)进行加固,若立柱EF的长为0.28米,则拱高OC为_____米
12 .如图,一次足球训练中,一球员从球门正前方将球射向球门,球射向球门的路线呈抛物线,当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米,当足球下落到离地面米时,足球飞行的水平距离为__________米.
13 .圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立平面直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点.已知雕塑OA高米,与OA水平距离5米处为水柱最高点,落水点C、D之间的距离为22米,则喷出水柱的最大高度为________米.
三、解答题(共48分)
14 .(8分)图中是抛物线形拱桥,当水面宽为4米时,拱顶距离水面2米;当水面高度下降1米时,水面宽度为多少米?
15 .(8分)如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的,正常水位时,大孔水面宽度为,顶点距水面,小孔顶点距水面.当水位上涨刚好淹没小孔时,求大孔的水面宽度.
16.(8分)如图,以一定的速度将小球沿与地面成一定角度的方向出击时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度(单位:)与飞行时间(单位:)之间具有二次函数关系.小明在一次击球过程中测得一些数据,如下表所示.
根据相关信息解答下列问题.
飞行时间 0 1 2
飞行高度 0 15 20
(1)求小球的飞行高度(单位:)关于飞行时间(单位:)的二次函数关系式;
(2)小球从飞出到落地要用多少时间?
(3)小球的飞行高度能否达到?如果能,请求出相应的飞行时间;如果不能,请说明理由.
17.(8分)如图,某城区公园有直径为7m的圆形水池,水池边安有排水槽,在中心O处修喷水装置,喷出水呈抛物线状,当水管OA高度在6m处时,距离OA水平距离1m处喷出的水流达到最大高度为8m.
(1)求抛物线解析式,并求水流落地点距离O点的距离;
(2)若不改变(1)中抛物线的形状和对称轴,若使水流落地点恰好落在圆形水池边排水槽内(不考虑边宽),则如何调节水管OA的高度?
18.(8分)某学校九年级的一场篮球比赛中,队员甲正在投篮,已知球出手时离地面高m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m.如图,设篮球运行轨迹为抛物线,篮圈距地面3m.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?
19.(8分)一隧道内设双行公路,隧道的高MN为6米.下图是隧道的截面示意图,并建立如图所示的直角坐标系,它是由一段抛物线和一个矩形CDEF的三条边围成的,矩形的长DE是8米,宽CD是2米.
(1)求该抛物线的解析式;
(2)为了保证安全,要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离.若行车道总宽度PQ(居中,两边为人行道)为6米,一辆高3.2米的货运卡车(设为长方形)靠近最右边行驶能否安全?请写出判断过程;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABHG,使H、G两点在抛物线上,A、B两点在地面DE上,设GH长为n米,“脚手架”三根木杆AG、GH、HB的长度之和为L,当n为何值时L最大,最大值为多少?
拓展培优*冲刺满分
1.如图,是某公园一圆形喷水池,在池中心竖直安装一根水管OA=1.25m,A处是喷头,水流在各个方向沿形状相同的抛物线落下,水落地后形成一个圆,圆心为O,直径为线段CB.建立如图所示的平面直角坐标系,若水流路线达到最高处时,到x轴的距离为2.25m,到y轴的距离为1m,则水落地后形成的圆的直径CB=_____m.
2 .一台自动喷灌设备的喷流情况如图所示,设水管在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线与y轴成角,水流最高点B比喷头A高2米.
(1)求抛物线解析式;
(2)求水流落地点C到O的距离;
(3)若水流的水平位移s米(抛物线上两对称点之间的距离)与水流的运动时间t之间的函数关系为,求共有几秒钟,水流的高度不低于2米?
九年级数学上分层优化堂堂清
二十二章 二次函数
22.3实际问题与二次函数
第三课时 抛物线型问题 (解析版)
学习目标:
1.能够从实际问题中抽象出二次函数模型,并运用二次函数及性质解决实际问题;
2.在探究二次函数的实际应用中学会分析问题,体会数学建模思想以及数学与生活的紧密联系性。
用二次函数解决抛物线型的一般步骤:
(1)恰当地建立直角坐标系;
(2)将已知条件转化为点的坐标;
(3)合理地设出所求函数关系式;
(4)代入已知条件或点的坐标,求出关系式;
(5)利用关系式求解问题.
二、利用二次函数解决抛物线型问题具体思路
这类问题所给的问题情境常有一个抛物线型物体,比如拱桥或隧道这些问题都可以通过构造二次承数的表达式来解决,解决这类问题般是利用数形结合思想和函数思想。
1.一般解题思路
(1)在示意图中建立适当的平面直角坐标系,将题目中所给条件转化平面直角坐标系中的坐标。
(2)根据图中坐标利用待定系数法求得二次函数的表达式。
(3)由二次函数的性质去分析解决问题,检验问题的结果是否符合实标意义,并作答。
2.卡车过拱桥(隧道)问题
在问题中,抛物线的函数表达式是首要条件,有时函数表达式已经给出,有时需要先求出来,求出函数表达式后有两种方法可以判断卡车能否从桥下通过:
(1)固定卡车的宽,看桥是否足够高(即相当于已知x的值,根据函数表达式求y的值,然后与限制的高的值比较大小);
(2)固定卡车的高,看桥是否足够宽(即相当于已知y的值,根据函数表达式求x的值,然后与限制的宽的值比较大小)
基础提升 教材核心知识点精练
知识点1:拱桥问题
【例1-1】郑州市彩虹桥新桥将于2023年9月底建成通车.新桥采用三跨连续单拱肋钢箱系杆拱桥,既保留了历史记忆,又展示出郑州的开放与创新.新桥的中跨大拱的拱肋可视为抛物线的一部分,桥面(视为水平的)与拱肋用垂直于桥面的系杆连接,测得拱肋的跨度为120米,与中点O相距30米处有一高度为27米的系杆.以所在直线为x轴,抛物线的对称轴为y轴建立如图②所示的平面直角坐标系.
(1)求抛物线的解析式;
(2)正中间系杆的长度是多少米?若相邻系杆之间的间距均为3米(不考虑系杆的粗细),是否存在一根系杆的长度恰好是长度的?请说明理由.
【答案】(1)
(2)正中间系杆的长度是36米,不存在一根系杆的长度恰好是OC长度的,理由见解析
【分析】(1)利用待定系数法求解即可;
(2)先求出正中间系杆的长度是36米,再建立方程求解即可.
【详解】(1)结合图象由题意可知:,,
设该抛物线解析式为:,
则:,
解得:,
∴.
(2)当时,,
∴正中间系杆的长度是36米.
设存在一根系杆的长度是的,即这根系杆的长度是12米,
则,
解得.
∵相邻系杆之间的间距均为3米,最中间系标在轴上,
∴每根系杆上的点的横坐标均为整数.
∴与实际不符.
∴不存在一根系杆的长度恰好是长度的.
【点评】本题考查了二次函数的实际应用,涉及到了待定系数法求函数解析式,解一元二次方程等知识,解题关键是读懂题意,找出数量关系,列出方程,并根据实际意义求解.
【例1-2】如图,有一个横截面为抛物线形状的隧道,隧道底部宽为,拱顶内高.把截面图形放在如图所示的平面直角坐标系中(原点O是的中点).
(1)求这条抛物线所对应的函数表达式;
(2)如果该隧道设计为车辆双向通行,规定车辆必须在中心黄线两侧行驶,那么一辆宽,高的大型货运卡车是否可以通过?为什么?
【答案】(1)
(2)一辆宽,高的大型货运卡车可以通过,理由见解析
【分析】(1)利用待定系数法求解即可;
(2)求出当时,x的值,再根据车辆宽且只能在中心的两侧行驶进行求解即可.
【详解】(1)解:由题意得,点C的坐标为,点A和点B的坐标分别为,
设抛物线解析式为,
把代入得,解得,
∴抛物线解析式为;
(2)解:一辆宽,高的大型货运卡车可以通过,理由如下:
在中,当时,解得,
∵,
∴,
∴一辆宽,高的大型货运卡车可以通过.
【点评】本题主要考查了二次函数的实际应用,正确求出对应的函数解析式是解题的关键.
知识点2:投球问题
【例2-1】掷实心球是中考体育考试项目之一.如图1是一名男生掷实心球情境,实心球行进路线是一条抛物线,行进高度与水平距离之间的函数关系如图2所示.掷出时,起点处高度为.当水平距离为时,实心球行进至最高点处.
(1)求y关于x的函数表达式;
(2)根据中考体育考试评分标准(男生版),投掷过程中,实心球从起点到落地点的水平距离大于等于时,即可得满分10分.该男生在此项考试中能否得满分,请说明理由.
【答案】(1)
(2)不能;理由见解析
【分析】(1)由图2可知,顶点坐标为,设二次函数表达式为,由此即可求解;
(2)令(1)中抛物线的解析式,且,解方程,即可求解.
【详解】(1)解:根据题意设关于的函数表达式为,
把代入解析式得,,
解得,,
∴关于的函数表达式为:,
即:.
(2)解:不能得满分,理由如下,
根据题意,令,且,
∴,
解方程得,,(舍去),
∵,
∴不能得满分.
【点评】本题主要考查二次函数的实际运用,掌握二次函数的性质及求解是解题的关键.
【例2-2】实心球是中考体育项目之一.在掷实心球时,实心球被掷出后的运动路线可以看作是抛物线的一部分,已知小军在一次掷实心球训练中,第一次投掷时出手点距地面1.8m,实心球运动至最高点时距地面3.4m,距出手点的水平距离为4m.设实心球掷出后距地面的竖直高度为y(m),实心球距出手点的水平距离为x(m).如图,以水平方向为x轴,出手点所在竖直方向为y轴建立平面直角坐标系.
(1)求第一次掷实心球时运动路线所在抛物线的表达式.
(2)若实心球投掷成绩(即出手点与着陆点的水平距离)达到12.4m为满分,请判断小军第一次投掷实心球能否得满分.
(3)第二次投掷时,实心球运动的竖直高度y与水平距离x近似满足函数关系.记小军第一次投掷时出手点与着陆点的水平距离为,第二次投掷时出手点与着陆点的水平距离为,则______(填“>”“<”“=”).
【答案】(1)
(2)不能得满分
(3)<
【分析】(1)设抛物线的表达式为,将代入解得a即可;
(2)令,解得x,与12.4m比较即可;
(3)令,解得x,根据(2)所得即可比较与.
【详解】(1)由题意,可知抛物线最高点的坐标为,
设抛物线的表达式为,
将代入,得,
解得.
∴第一次掷实心球时运动路线所在抛物线的表达式为;
(2)令,解得(负值已舍去),
∴实心球出手点与着陆点的水平距离为m.
∵,即,∴,
∴小军第一次投掷实心球不能得满分.
(3)∵,
解得(负值已舍去),
,,
,,
∴.
故答案为:<.
【点评】本题考查二次函数的应用以及待定系数法求解析式,熟练掌握二次函数的性质是解题的关键.
知识点3:喷水问题
【例3-1】一名运动员在高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面的高度与离起跳点A的水平距离之间的函数关系如图所示,运动员离起跳点A的水平距离为时达到最高点,当运动员离起跳点A的水平距离为时离水面的距离为.
(1)求y关于x的函数表达式;
(2)求运动员从起跳点到入水点的水平距离的长.
【答案】(1)y关于x的函数表达式为;
(2)运动员从起跳点到入水点的水平距离的长为.
【分析】(1)由题意得抛物线的对称轴为,经过点,,利用待定系数法即可求解;
(2)令,解方程即可求解.
【详解】(1)解:由题意得抛物线的对称轴为,经过点,,
设抛物线的表达式为,
∴,解得,
∴y关于x的函数表达式为;
(2)解:令,则,
解得(负值舍去),
∴运动员从起跳点到入水点的水平距离的长为.
【点睛】本题考查了二次函数在实际问题中的应用,数形结合并熟练掌握运用待定系数法求抛物线的解析式是解题的关键.
【例3-2】如图①,有一移动灌溉装置喷出水柱的路径可近似地看作一条抛物线,该灌溉装置的喷水头到水平地面的距离为1米,喷出的抛物线形水柱对称轴为直线.用该灌溉装置灌溉一坡地草坪,其水柱的高度y(单位:米)与水柱落地处距离喷水头的距离x(单位:米)之间的函数关系式为,其图像如图②所示.已知坡地所在直线经过点.
(1)的值为______;
(2)若,求水柱与坡面之间的最大铅直高度;
(3)若点B横坐标为18,水柱能超过点B,则a的取值范围为______;
(4)若时,到喷水头水平距离为16米的A处有一棵新种的银杏树需要被灌溉,园艺工人将灌溉装置水平向后移动4米,试判断灌溉装置能否灌溉到这棵树,并说明理由.
【答案】(1)1
(2)水柱与坡面之间的最大铅直高度为米
(3)
(4)水平向后移动4米,不能灌溉到这棵树,理由见解析
【分析】(1)代入抛物线与y轴的交点的坐标即可求解;
(2)根据已知条件求出抛物线解析式及直线解析式,设抛物线上一点P点横坐标为t,作作轴交于点Q,用t表示P点和Q点的坐标,并计算的长度,建立关于t的二次函数,在取值范围内求最大值即可;
(3)代入B点横坐标到一次函数解析式,求出对应纵坐标;代入点、抛物线对称轴及B点横坐标到二次函数解析式,建立不等式进行求解;
(4)根据平移求得平移后的抛物线解析式,代入到抛物线解析式和直线解析式进行对比即可.
【详解】(1)代入到抛物线解析式,得:;
故答案为:1;
(2)设抛物线的解析式为
将点代入,得
抛物线的解析式为
即
坡地经过点
的解析式为
如解图,
设抛物线上一点,过点P作轴交于点Q,
则,的长为
,
函数图像开口向下,d有最大值
根据顶点公式当时,有最大值
水柱与坡面之间的最大铅直高度为米;
故答案为:水柱与坡面之间的最大铅直高度为米;
(3)由(2)知,直线的解析式为,
时,
,
抛物线的解析式为,即,
当时,,要使水柱能超过点B则,
解得
故答案为:;
(4)不能;
当灌溉装置水平向后移动4米时,由(2)可得平移后的抛物线解析式为.
将代入抛物线解析式,得,
将代入直线OB解析式,得
水平向后移动4米,不能灌溉到这棵树.
【点评】本题考查二次函数的实际应用,掌握待定系数法求解二次函数解析式和直线解析式、平移规律求二次函数解析式、根据坐标关系及二次函数求线段最大值是解题的关键.
能力强化 能力强化训练
1.一隧道内设双行公路,隧道的高MN为6米.下图是隧道的截面示意图,并建立如图所示的直角坐标系,它是由一段抛物线和一个矩形CDEF的三条边围成的,矩形的长DE是8米,宽CD是2米.
(1)求该抛物线的解析式;
(2)为了保证安全,要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离.若行车道总宽度PQ(居中,两边为人行道)为6米,一辆高3.2米的货运卡车(设为长方形)靠近最右边行驶能否安全?请写出判断过程;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABHG,使H、G两点在抛物线上,A、B两点在地面DE上,设GH长为n米,“脚手架”三根木杆AG、GH、HB的长度之和为L,当n为何值时L最大,最大值为多少?
【答案】(1)y=-x2+4;(2)能安全通过,见解析;(3)n=4时,L有最大值,最大值为14
【分析】(1)根据题意和函数图象,可以设出抛物线的解析式,然后根据抛物线过点F和点M即可求得该抛物线的解析式;
(2)先求出抛物线的解析式,再根据题意判断该隧道能通过的车辆的最高高度,便可判断该车辆能安全通过.
(3)射出H的坐标,用n表示出L,利用二次函数的性质求解即可.
【详解】解:(1)由题意得M(0,4),F(4,0)
可设抛物线的解析式为y=ax2+4,
将F(4,0)代入y=ax2+4中,得a=-,
∴抛物线的解析式为y=-x2+4;
(2)当x=3,y=,
+2-=3.253.2,∴能安全通过;
(3)由GH=n,可设H(),
∴GH+GA+BH=n+()×2+2×2=,
∴L=,
∵a<0,抛物线开口向下,
∴当n=-=4时,L有最大值,最大值为14.
【点评本题考查了二次函数的实际应用,解题的关键是要注意自变量的取值范围必须使实际问题有意义.
2.北方的冬天,人们酷爱冰雪运动,在这项运动里面,我们可以用数学知识解决一些实际问题.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系如图所示,图中的抛物线近似表示滑雪场地上的一座小山坡,某运动员从点O正上方50米处的A点滑出,滑出后沿一段抛物线运动.当运动员运动到离A处的水平距离为60米时,离水平线的高度为60米.
(1)求小山坡最高点到水平线的距离.
(2)求抛物线所对应的函数表达式.
(3)当运动员滑出点A后,直接写出运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为10米.
【答案】(1)40米
(2)
(3)运动员运动的水平距离为为米时,运动员与小山坡的竖直距离为10米
【分析】(1)由抛物线的解析式得出最大值即可;
(2)把、代入可得抛物线所对应的函数表达式;
(3)根据纵坐标的差为10,列出方程可得答案.
【详解】(1)解:由,得
当时,y有最大值为40.
∴小山坡最高点到水平线的距离为40米.
(2)解:把、代入中,得
得解得
∴抛物线所对应的函数表达式.
(3)解:设运动员运动的水平距离是x米,
此时小山坡的高度是,
运动员运动的水平高度是,
∴,
解得或0(舍去),
答:运动员运动的水平距离为米时,运动员与小山坡的竖直距离为10米.
【点评】本题考查二次函数的基本性质及其应用,熟练掌握二次函数的基本性质,并能将实际问题与二次函数模型相结合是解决本题的关键.
堂堂清
一、选择题(每小题4分,共32分)
1.小明在体育训练中掷出的实心球的运动路线呈如图所示的抛物线形,若实心球运动的抛物线的表达式为,其中是实心球飞行的高度,是实心球飞行的水平距离,则小明此次郑球过程中,实心球的最大高度是( )
A. B. C. D.
【答案】B
【分析】由可得抛物线的顶点坐标为:,结合函数的性质可得答案.
【详解】解:∵,
∴抛物线的顶点坐标为:,
∵,
∴实心球的最大高度是,
故选B.
【点评】本题考查的是抛物线的图像与性质,掌握“利用顶点式求解抛物线的顶点坐标或函数的最值”是解本题的关键.
2.向空中发射一枚炮弹,经过秒后高度为米,且时间与高度的关系式为,若炮弹在第6秒与第14秒时的高度相等,则炮弹所在高度最高的时间是( )
A.第8秒 B.第9秒 C.第10秒 D.第11秒
【答案】C
【分析】本题先根据题意求出抛物线的对称轴,即可得出顶点的横坐标,从而得出跑弹所在高度最高时的值.
【详解】解:∵此炮弹在第6与第14秒时的高度相等,
∴抛物线的对称轴是直线,
∴炮弹所在高度最高是10秒,
故选:C.
【点评】本题主要考查了二次函数的应用,在解题时要能根据题意求出抛物线的对称轴得出答案是本题的关键.
3 .如图,一个移动喷灌架喷射出的水流可以近似地看成抛物线,喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度1.8米,水流喷射的最远水平距离是( )
A.20米 B.18米 C.10米 D.8米
【答案】A
【分析】根据顶点式求得抛物线解析式,进而求得与轴的交点坐标即可求解.
【详解】解:∵喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度1.8米,
设抛物线解析式为,将点代入,得
解得
∴抛物线解析式为
令,解得(负值舍去)
即,
故选:A
【点评】本题考查了二次函数的实际应用,根据题意求得解析式是解题的关键.
4.有一拱桥洞呈抛物线形,这个桥洞的最大高度是16m,跨度为40m,现把它的示意图(如图)放在坐标系中,则抛物线的解析式为( )
A.y=x2+x B.y=-x2+x
C.y=-x2-x D.y=-x2+x+16
【答案】B
【分析】根据题意设出顶点式,将原点代入即可解题.
【详解】解:由图可知,该抛物线开口向下,对称轴为x=20,
最高点坐标为(20,16),且经过原点,
由此可设该抛物线解析式为,
将原点坐标代入可得,
解得:,
故该抛物线解析式为
故选:B.
【点评】本题主要考查二次函数图像性质的实际应用、二次函数顶点式等,找到顶点坐标设出顶点式是解题关键.
如图,某大门的形状是一抛物线形建筑,大门的地面宽8 m,在两侧距地面3.5 m高处有两个挂单位名牌匾用的铁环,两铁环的水平距离是6 m.若按图所示建立平面直角坐标系,则抛物线的解析式是( ).(建筑物厚度忽略不计)
A. B. C. D.
【答案】A
【分析】先根据函数图象可得抛物线与轴的两个交点坐标为和,再设抛物线的解析式为,将点代入即可得.
【详解】解:由函数图象可知,抛物线与轴的两个交点坐标为和,且经过点,
设抛物线的解析式为,
将点代入得:,
解得,
则抛物线的解析式为,即为,
故选:A.
【点评】本题考查了求抛物线的解析式,熟练掌握待定系数法是解题关键.
6.小明在期末体育测试中掷出的实心球的运动路线呈抛物线形.若实心球运动的抛物线的解析式为,其中y是实心球飞行的高度,x是实心球飞行的水平距离.已知该同学出手点A的坐标为,则实心球飞行的水平距离OB的长度为( )
A.7m B.7.5m C.8m D.8.5m
【答案】C
【分析】根据题意待定系数法求解析式,再令,即可求解.
【详解】解:∵实心球运动的抛物线的解析式为,点A的坐标为,
∴,
解得,
,
令,,
即,
解得(舍去),
故选:C.
【点评】本题考查了二次函数的应用,待定系数法求解析式,求二次函数与坐标轴的交点,掌握二次函数的性质是解题的关键.
7.如图是抛物线形的拱桥,当水面宽4m时,顶点离水面2m,当水面宽度增加到6m时,水面下降( )
A.1m B.1.5m C.2.5m D.2m
【答案】C
【分析】根据已知得出直角坐标系,进而求出二次函数的解析式,再把代入抛物线的解析式得出水面宽度,即可得出答案.
【详解】解:建立平面直角坐标系,设横轴通过,纵轴通过中点且通过顶点,则通过画图可得知为原点,
由平面直角坐标系可知,,即,
设抛物线的解析式为,
将点代入得:,解得,
则抛物线的解析式为,即,
当时,,
所以水面下降,
故选:C.
【点评】本题主要考查了二次函数的应用,根据已知建立平面直角坐标系从而得出二次函数的解析式是解决问题的关键.
8 .如图,从某建筑物10m高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直).如果抛物线的最高点M离墙1m,离地面m,则水流落地点B离墙的距离OB是( )
A.2m B.3m C.4m D.5m
【解答】解:设抛物线的解析式为y=a(x﹣1)2+,由题意,得
10=a+,
a=﹣.
∴抛物线的解析式为:y=﹣(x﹣1)2+.
当y=0时,
0=﹣(x﹣1)2+,
解得:x1=﹣1(舍去),x2=3.
OB=3m.
故选:B.
二、填空题(每小题4分,共20分)
9..如图,一位篮球运动员投篮,球沿抛物线运行,然后准确落入篮筐内,已知篮筐的中心离地面的高度为,则他距篮筐中心的水平距离是 .
【答案】4
【分析】将代入中可求出x,结合图形可知,即可求出OH.
【详解】解:当时,,解得:或,
结合图形可知:,
故答案为:4
【点评】本题考查二次函数的实际应用:投球问题,解题的关键是结合函数图形确定x的值.
10 .中国羽毛球队蝉联苏迪曼杯团体赛冠军,成就了首个五连冠霸业.比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y(米)与水平距离x(米)之间满足关系,则羽毛球飞出的水平距离为 米.
【答案】5
【分析】试题分析:根据羽毛球飞出的水平距离即为抛物线与x轴正半轴交点到原点的距离求出即可.
【详解】当y=0时,,
解得:x1=﹣1(舍),x2=5.
∴羽毛球飞出的水平距离为5米.
11 .如图,某单位的围墙由一段段形状相同的抛物线形栅栏组成,为了牢固,每段栅栏间隔0.2米设置一根立柱(即AB间间隔0.2米的7根立柱)进行加固,若立柱EF的长为0.28米,则拱高OC为_____米
【答案】0.64
【分析】根据抛物线,建立直角坐标系,求出抛物线解析式,即可求得OC的长.
【详解】
解:如图,以点C为坐标系原点,OC所在直线为y轴,建立直角坐标系.
设抛物线的解析式为,
由题意可知:点A的横坐标为-0.8,点F的横坐标为-0.6,
代入,
有,,
点A的纵坐标即为OC的长,
∴0.36a+0.28=0.64a,
解得a=1,
∴抛物线解析式为,
,
故OC的长为:0.64m.
【点评】本题考查根据抛物线构建直角坐标系,解决实际问题,熟练掌握二次函数相关知识点是解题的关键.
12 .如图,一次足球训练中,一球员从球门正前方将球射向球门,球射向球门的路线呈抛物线,当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米,当足球下落到离地面米时,足球飞行的水平距离为__________米.
【答案】10
【分析】设抛物线的解析式为,代入原点,确定解析式为,当y=米时,求得x的值即可.
【详解】设抛物线的解析式为,代入原点,得:
,
解得a=,
∴抛物线的解析式为,
当y=米时,
,
解得x=10,x=2(舍去),
足球飞行的水平距离为10米,
故答案为:10.
【点评】本题考查了抛物线的解析式,已知函数值求自变量值,熟练掌握待定系数法是解题的关键.
13 .圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立平面直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点.已知雕塑OA高米,与OA水平距离5米处为水柱最高点,落水点C、D之间的距离为22米,则喷出水柱的最大高度为________米.
【答案】6
【分析】设水柱所在抛物线的函数表达式为 (x≥0),根据题意得到A(0,),D(11,0),对称轴x=5,用待定系数法求出函数表达式,把x=5代入,即可得到喷出水柱的最大高度.
【详解】解:设水柱所在抛物线的函数表达式为 (x≥0),
∵雕塑OA高米,
∴点A的坐标是(0,),
∵落水点C、D之间的距离为22米,
∴点D的坐标为(11,0),
∵与OA水平距离5米处为水柱最高点,
∴抛物线的对称轴为x=5,
得到
解得
∴水柱所在抛物线的函数表达式为 (x≥0)
当x=5时,,
∴ 喷出水柱的最大高度为6米,
故答案为:6
【点评】本题考查了二次函数的实际应用,待定系数法求出函数表达式是基础,求出函数的最大值是关键。
三、解答题(共48分)
14 .(8分)图中是抛物线形拱桥,当水面宽为4米时,拱顶距离水面2米;当水面高度下降1米时,水面宽度为多少米?
【答案】
【分析】根据已知得出直角坐标系,进而求出二次函数解析式,再根据通过把y=-1代入抛物线解析式得出水面宽度,即可得出答案.
【详解】解:建立平面直角坐标系.设二次函数的解析式为(a≠0).
∵图象经过点(2,-2),
∴-2=4a,
解得:.
∴.
当y=-3时,.
答:当水面高度下降1米时,水面宽度为米.
【点睛】此题主要考查了二次函数的应用,根据已知建立坐标系从而得出二次函数解析式是解决问题的关键,难度一般.
15 .(8分)如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的,正常水位时,大孔水面宽度为,顶点距水面,小孔顶点距水面.当水位上涨刚好淹没小孔时,求大孔的水面宽度.
【答案】此时大孔的水面宽度为10m.
【分析】根据题意,建立如图所示的平面直角坐标系,可以得到A、B、M的坐标,设出函数关系式,待定系数求解函数式.根据NC的长度,得出函数值y,代入解析式,即可得出E、F的坐标,进而得出答案.
【详解】解:如图,建立如图所示的平面直角坐标系,由题意得,M点坐标为(0,6),A点坐标为(-10,0),B点坐标为(10,0),
设中间大抛物线的函数式为y=ax2+6,
∵点B在此抛物线上,
∴0=a×102+6,
解得a=-,
∴函数式为y=-x2+6.
∵NC=4.5m,
∴令y=4.5,
代入解析式得-x2+6=4.5,
x1=5,x2=-5,
∴可得EF=5-(-5)=10.
此时大孔的水面宽度为10m.
【点评】本题是二次函数的实际应用,考查了待定系数法求二次函数的解析式,由函数值求自变量的值,解答时求出函数的解析式是关键.
16.(8分)如图,以一定的速度将小球沿与地面成一定角度的方向出击时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度(单位:)与飞行时间(单位:)之间具有二次函数关系.小明在一次击球过程中测得一些数据,如下表所示.
根据相关信息解答下列问题.
飞行时间 0 1 2
飞行高度 0 15 20
(1)求小球的飞行高度(单位:)关于飞行时间(单位:)的二次函数关系式;
(2)小球从飞出到落地要用多少时间?
(3)小球的飞行高度能否达到?如果能,请求出相应的飞行时间;如果不能,请说明理由.
【答案】(1)
(2)
(3)不能,理由见解析
【分析】(1)利用待定系数法即可求解;
(2)令h=0即可求解;
(3)令,得到方程无解即可判断.
(1)
由题意可设关于的二次函数关系式为,
因为当,2时,,20,
∴,
解得:.
∴关于的二次函数关系式为.
(2)
当,,解得:,.
∴小球从飞出到落地所用的时间为.
(3)
小球的飞行高度不能达到.
理由如下:
当时,,方程即为,
∵,
∴此方程无实数根.
即小球飞行的高度不能达到.
【点评】此题主要考查一元二次方程与二次函数的实际应用,解题的关键是根据题意求出函数解析式,再根据题意进行解答.
17.(8分)如图,某城区公园有直径为7m的圆形水池,水池边安有排水槽,在中心O处修喷水装置,喷出水呈抛物线状,当水管OA高度在6m处时,距离OA水平距离1m处喷出的水流达到最大高度为8m.
(1)求抛物线解析式,并求水流落地点距离O点的距离;
(2)若不改变(1)中抛物线的形状和对称轴,若使水流落地点恰好落在圆形水池边排水槽内(不考虑边宽),则如何调节水管OA的高度?
【解答】解:(1)∵抛物线的顶点为(1,8),
∴设抛物线的解析式为y=a(x﹣1)2+8,
把A(0,6)代入可得a=﹣2,
∴解析式为y=﹣2(x﹣1)2+8,
当y=0时,x=3或﹣1(舍去),
答:解析式为y=﹣2(x﹣1)2+8,水流落地点距离O点的距离是3米;
(2)抛物线的表达式为y=﹣2(x﹣1)2+k,
把(3.5,0)代入可得k=12.5,
∴解析式为y=﹣2(x﹣1)2+12.5,
当x=0时,y=10.5,
答:水管OA的高度调整为10.5米.
18.(8分)某学校九年级的一场篮球比赛中,队员甲正在投篮,已知球出手时离地面高m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m.如图,设篮球运行轨迹为抛物线,篮圈距地面3m.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?
【答案】(1)能准确投中,理由见解析
(2)乙能盖帽拦截成功,理由见解析
【分析】(1)根据抛物线的顶点坐标及球出手时的坐标,由待定系数法可确定抛物线的解析式,令,求出y的值,与3m比较即可作出判断;
(2)将代入,进而得出答案.
【详解】(1)解:球出手点、最高点、篮圈坐标分别为,
设这条抛物线对应的函数解析式为,
将点代入,可得,解得,
∴,
当时,,
∴此球能准确投中;
(2)当时,,
∴乙能盖帽拦截成功.
【点睛】本题主要考查了二次函数实际应用,根据题意求得函数解析式,掌握二次函数的性质是解题的关键.
19.(8分)一隧道内设双行公路,隧道的高MN为6米.下图是隧道的截面示意图,并建立如图所示的直角坐标系,它是由一段抛物线和一个矩形CDEF的三条边围成的,矩形的长DE是8米,宽CD是2米.
(1)求该抛物线的解析式;
(2)为了保证安全,要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离.若行车道总宽度PQ(居中,两边为人行道)为6米,一辆高3.2米的货运卡车(设为长方形)靠近最右边行驶能否安全?请写出判断过程;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABHG,使H、G两点在抛物线上,A、B两点在地面DE上,设GH长为n米,“脚手架”三根木杆AG、GH、HB的长度之和为L,当n为何值时L最大,最大值为多少?
【答案】(1)y=-x2+4;(2)能安全通过,见解析;(3)n=4时,L有最大值,最大值为14
【分析】(1)根据题意和函数图象,可以设出抛物线的解析式,然后根据抛物线过点F和点M即可求得该抛物线的解析式;
(2)先求出抛物线的解析式,再根据题意判断该隧道能通过的车辆的最高高度,便可判断该车辆能安全通过.
(3)射出H的坐标,用n表示出L,利用二次函数的性质求解即可.
【详解】解:(1)由题意得M(0,4),F(4,0)
可设抛物线的解析式为y=ax2+4,
将F(4,0)代入y=ax2+4中,得a=-,
∴抛物线的解析式为y=-x2+4;
(2)当x=3,y=,
+2-=3.253.2,∴能安全通过;
(3)由GH=n,可设H(),
∴GH+GA+BH=n+()×2+2×2=,
∴L=,
∵a<0,抛物线开口向下,
∴当n=-=4时,L有最大值,最大值为14.
【点睛】本题考查了二次函数的实际应用,解题的关键是要注意自变量的取值范围必须使实际问题有意义.
拓展培优*冲刺满分
1.如图,是某公园一圆形喷水池,在池中心竖直安装一根水管OA=1.25m,A处是喷头,水流在各个方向沿形状相同的抛物线落下,水落地后形成一个圆,圆心为O,直径为线段CB.建立如图所示的平面直角坐标系,若水流路线达到最高处时,到x轴的距离为2.25m,到y轴的距离为1m,则水落地后形成的圆的直径CB=_____m.
【答案】5
【分析】设y轴右侧的抛物线解析式为:y=a(x 1)2+2.25,将A(0,1.25)代入,求得a,从而可得抛物线的解析式,再令函数值为0,解方程可得点B坐标,从而可得CB的长.
【详解】解:设y轴右侧的抛物线解析式为:y=a(x﹣1)2+2.25
∵点A(0,1.25)在抛物线上
∴1.25=a(0﹣1)2+2.25
解得:a=﹣1
∴抛物线的解析式为:y=﹣(x﹣1)2+2.25
令y=0得:0=﹣(x﹣1)2+2.25
解得:x=2.5或x=﹣0.5(舍去)
∴点B坐标为(﹣2.5,0)
∴OB=OC=2.5
∴CB=5
故答案为:5.
【点评】本题考查了二次函数在实际问题中的应用,明确二次函数的相关性质及正确的解方程,是解题的关键.
2 .一台自动喷灌设备的喷流情况如图所示,设水管在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线与y轴成角,水流最高点B比喷头A高2米.
(1)求抛物线解析式;
(2)求水流落地点C到O的距离;
(3)若水流的水平位移s米(抛物线上两对称点之间的距离)与水流的运动时间t之间的函数关系为,求共有几秒钟,水流的高度不低于2米?
【答案】(1)y= 0.5(x 2)2+3.5;(2)2+;(3)
【分析】(1)作BD⊥y轴于点D,由∠DAB=45°,就可以求出AD=BD=2,就可以求出B的坐标,设抛物线的解析式为y=a(x 2)2+3.5,由待定系数法求出其解即可;
(2)当y=0时代入(1)的解析式求出其解即可;
(3)当y=2时代入(1)的解析式求出s的值,再将s的值代入t=0.8s求出t的值即可.
【详解】解:(1)作BD⊥y轴于点D,
∴∠ADB=90°.
∵∠DAB=45°,
∴∠ABD=∠DBA=45°,
∴AD=BD=2,
∵OA=1.5,
∴B(2,3.5),A(0,1.5).
设抛物线的解析式为y=a(x 2)2+3.5,由题意,得
1.5=4a+3.5,
解得:a= 0.5.
∴y= 0.5(x 2)2+3.5.
答:抛物线解析式为y= 0.5(x 2)2+3.5;
(2)当y=0时,
0= 0.5(x 2)2+3.5.
解得:x1=2+,x2=2 (舍去),
∴水流落地点C到O点的距离为2+;
(3)当y=2时,
2= 0.5(x 2)2+3.5.
解得:x3=2+,x4=2 ,
∴水流位移的距离为:2+ (2 )=2,
∴t=0.8×2=,
∴共有秒钟,水流高度不低于2米.
【点评】本题考查了待定系数法求二次函数的解析式的运用,顶点式的运用,由函数值求自变量的值的运用,解答时求出二次函数的解析式是关键.
老师对你说:
老师对你说:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
