3.2.1单调性与最大小值(第2课时) 课件(共15张PPT)
文档属性
| 名称 | 3.2.1单调性与最大小值(第2课时) 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-11 09:52:34 | ||
图片预览




文档简介
(共15张PPT)
3.2.1 单调性与最大(小)值
第二课时
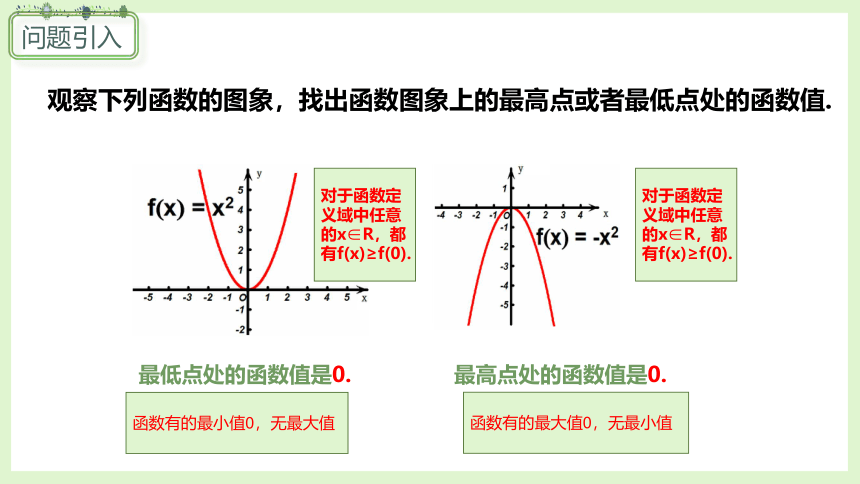
观察下列函数的图象,找出函数图象上的最高点或者最低点处的函数值.
最低点处的函数值是0.
最高点处的函数值是0.
对于函数定义域中任意的x∈R,都有f(x)≥f(0).
对于函数定义域中任意的x∈R,都有f(x)≥f(0).
函数有的最小值0,无最大值
函数有的最大值0,无最小值
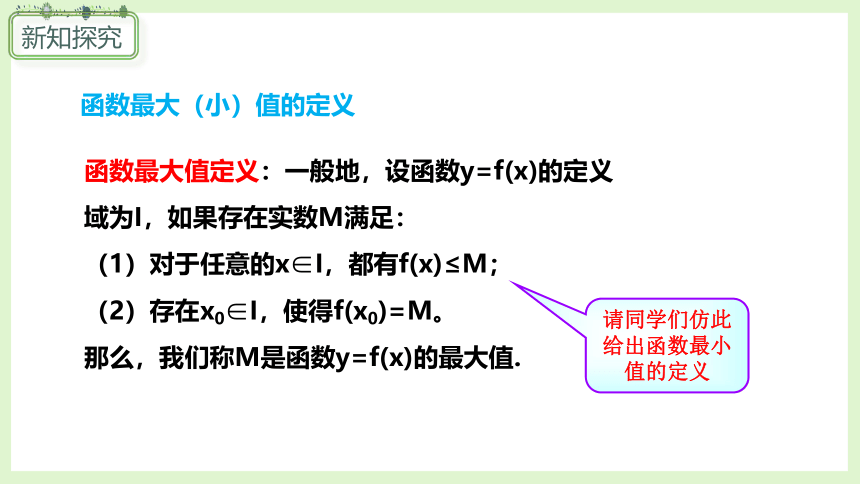
函数最大(小)值的定义
函数最大值定义:一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
(1)对于任意的x∈I,都有f(x)≤M;
(2)存在x0∈I,使得f(x0)=M。
那么,我们称M是函数y=f(x)的最大值.
请同学们仿此给出函数最小值的定义
函数最小值的定义:一般地,设函数y=f(x)的定义域为I,如果存在实数N满足:
(1)对任意的 ,都有 ;
(2)存在 ,使得 .
那么,我们就称N是函数y=f(x)的最小值.
对函数最值的理解
1.最大值定义里的两个条件:
(1)对于任意的x∈I,都有f(x)≤M;(2)存在x0∈I,使得f(x0)=M。
两条件缺一不可;
2.函数的最值是函数在定义域上的整体性质,即这个函数值是函数在整个定义域上的最大的函数值或者是最小的函数值.
3.不是所有的函数在其定义域上都有最大或最小值,但若函数图像在某个闭区间上连续,则函数在该区间上一定有最大、最小值,最值可能在区间端点取到,也可能在区间内部取到
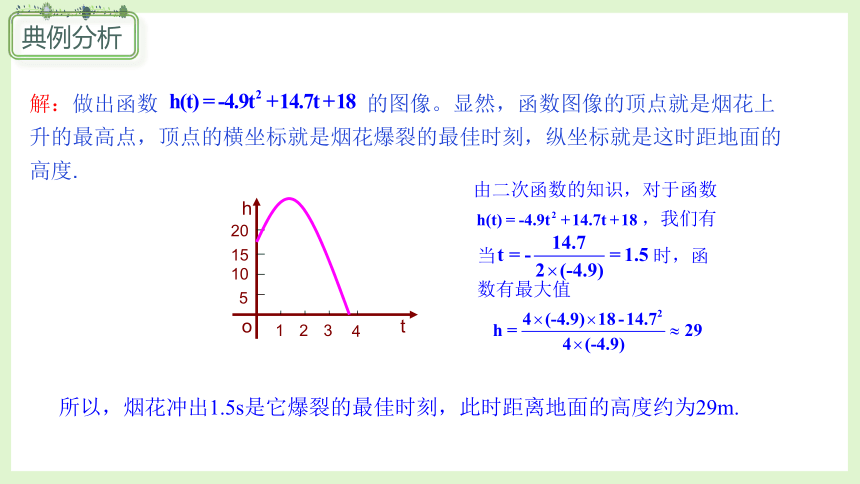
例3.“菊花”烟花是最壮观的烟花之一.制造时一般是期望在它达到最高点时爆裂.如果烟花距地面的高度h m与时间t s之间的关系为h(t)=-4.9t2+14.7t+18,那么烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少(精确到1 m)?
解:做出函数 的图像。显然,函数图像的顶点就是烟花上升的最高点,顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度.
o
t
h
4
3
2
1
5
10
15
20
由二次函数的知识,对于函数
,我们有
当 时,函数有最大值
所以,烟花冲出1.5s是它爆裂的最佳时刻,此时距离地面的高度约为29m.
例4.已知函数 ,求函数f(x)的最大值和最小值。
解:设x1,x2是区间[2,6]上的任意两个实数,且x1先证明单调性
分析:由函数的图象可知道,此函数在[2,6]上递减。所以在区间[2,6]的两个端点上分别取得最大值与最小值.
所以,函数 是区间[2,6]上的减函数.
因此,函数 在区间[2,6]的两个端点上分别取得最大值与最小值,即在x=2时取得最大值,最大值是2,在x=6时取得最小值,最小值是0.4.
函数在定义域上是减函数必需进行证明,然后再根据这个单调性确定函数取得最值的点.因此解题过程分为两个部分,证明函数在[2,6]上是减函数,求这个函数的最大值和最小值.
求函数 在区间[0,3]的最大值和最小值。
【提示】证明函数在区间[0,3]上是减函数.
【答案】最大值是2,最小值是 .
1.求函数f(x)=kx+2在区间[0,2]上的最大值和最小值.
【提示】当k=0时,函数是常数函数;当k≠0时函数是一次函数,再根据k>0,k<0时函数的单调性进行解答.
【答案】k=0时,函数的最大值和最小值都是2;
k>0时,函数的最小值是2,最大值是2k+2;
k<0时,函数的最小值是2k+2,最大值是2.
2.函数f(x)=x2+4ax+2在区间 (-∞,6]内递减,则a的取值范围是( )
(A)a≥3 (B)a≤3
(C)a≥-3 (D)a≤-3
D
3.已知函数f(x)=4x2-mx+1在(-∞,-2]上递减,在[-2,
+∞)上递增,则f(x)在[1,2]上的值域为____________.
[21,49]
1.函数的最值是函数的基本性质之一,函数的最值是函数在其定义域上的整体性质.
2.根据函数的单调性确定函数最值时,如果是一般的函数要证明这个函数的单调性,若是基本的函数可以直接使用函数的单调性.
3.含有字母系数的函数,在求其最值时要注意分情况讨论,画出函数的图象有利于问题的解决.
3.2.1 单调性与最大(小)值
第二课时
观察下列函数的图象,找出函数图象上的最高点或者最低点处的函数值.
最低点处的函数值是0.
最高点处的函数值是0.
对于函数定义域中任意的x∈R,都有f(x)≥f(0).
对于函数定义域中任意的x∈R,都有f(x)≥f(0).
函数有的最小值0,无最大值
函数有的最大值0,无最小值
函数最大(小)值的定义
函数最大值定义:一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
(1)对于任意的x∈I,都有f(x)≤M;
(2)存在x0∈I,使得f(x0)=M。
那么,我们称M是函数y=f(x)的最大值.
请同学们仿此给出函数最小值的定义
函数最小值的定义:一般地,设函数y=f(x)的定义域为I,如果存在实数N满足:
(1)对任意的 ,都有 ;
(2)存在 ,使得 .
那么,我们就称N是函数y=f(x)的最小值.
对函数最值的理解
1.最大值定义里的两个条件:
(1)对于任意的x∈I,都有f(x)≤M;(2)存在x0∈I,使得f(x0)=M。
两条件缺一不可;
2.函数的最值是函数在定义域上的整体性质,即这个函数值是函数在整个定义域上的最大的函数值或者是最小的函数值.
3.不是所有的函数在其定义域上都有最大或最小值,但若函数图像在某个闭区间上连续,则函数在该区间上一定有最大、最小值,最值可能在区间端点取到,也可能在区间内部取到
例3.“菊花”烟花是最壮观的烟花之一.制造时一般是期望在它达到最高点时爆裂.如果烟花距地面的高度h m与时间t s之间的关系为h(t)=-4.9t2+14.7t+18,那么烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少(精确到1 m)?
解:做出函数 的图像。显然,函数图像的顶点就是烟花上升的最高点,顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度.
o
t
h
4
3
2
1
5
10
15
20
由二次函数的知识,对于函数
,我们有
当 时,函数有最大值
所以,烟花冲出1.5s是它爆裂的最佳时刻,此时距离地面的高度约为29m.
例4.已知函数 ,求函数f(x)的最大值和最小值。
解:设x1,x2是区间[2,6]上的任意两个实数,且x1
分析:由函数的图象可知道,此函数在[2,6]上递减。所以在区间[2,6]的两个端点上分别取得最大值与最小值.
所以,函数 是区间[2,6]上的减函数.
因此,函数 在区间[2,6]的两个端点上分别取得最大值与最小值,即在x=2时取得最大值,最大值是2,在x=6时取得最小值,最小值是0.4.
函数在定义域上是减函数必需进行证明,然后再根据这个单调性确定函数取得最值的点.因此解题过程分为两个部分,证明函数在[2,6]上是减函数,求这个函数的最大值和最小值.
求函数 在区间[0,3]的最大值和最小值。
【提示】证明函数在区间[0,3]上是减函数.
【答案】最大值是2,最小值是 .
1.求函数f(x)=kx+2在区间[0,2]上的最大值和最小值.
【提示】当k=0时,函数是常数函数;当k≠0时函数是一次函数,再根据k>0,k<0时函数的单调性进行解答.
【答案】k=0时,函数的最大值和最小值都是2;
k>0时,函数的最小值是2,最大值是2k+2;
k<0时,函数的最小值是2k+2,最大值是2.
2.函数f(x)=x2+4ax+2在区间 (-∞,6]内递减,则a的取值范围是( )
(A)a≥3 (B)a≤3
(C)a≥-3 (D)a≤-3
D
3.已知函数f(x)=4x2-mx+1在(-∞,-2]上递减,在[-2,
+∞)上递增,则f(x)在[1,2]上的值域为____________.
[21,49]
1.函数的最值是函数的基本性质之一,函数的最值是函数在其定义域上的整体性质.
2.根据函数的单调性确定函数最值时,如果是一般的函数要证明这个函数的单调性,若是基本的函数可以直接使用函数的单调性.
3.含有字母系数的函数,在求其最值时要注意分情况讨论,画出函数的图象有利于问题的解决.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
