人教版高中数学选择性必修第三册第八章成对数据的统计分析 A卷基础训练(含解析)
文档属性
| 名称 | 人教版高中数学选择性必修第三册第八章成对数据的统计分析 A卷基础训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 370.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-11 10:07:46 | ||
图片预览




文档简介
成套的课件成套的教案成套的试题尽在高中数学同步资源大全QQ群483122854
人教版高中数学选择性必修第三册
第八章成对数据的统计分析A卷基础训练(原卷版)
一、选择题
1.(2021·全国高二课时练)某同学为了解气温对热饮销售的影响,经过统计分析,得到了一个卖出的热饮杯数与当天气温的回归方程.下列选项正确的是( )
A.与线性正相关 B.与线性负相关
C.随增大而增大 D.随减小而减小
2.(2021·全国高二课时练)如表是一个2×2列联表:则表中a,b的值分别为( )
y1 y2 合计
x1 a 21 73
x2 22 25 47
合计 b 46 120
A.94,72 B.52,50 C.52,74 D.74,52
3.(2021·无锡市才智教育培训中心高二月考)春节期间,“履行节约,反对浪费”之风悄然吹开,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:
做不到“光盘” 能做到“光盘”
男 45 10
女 30 15
附:χ2=,其中n=a+b+c+d为样本容量.
α 0.10 0.05 0.025
xα 2.706 3.841 5.024
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.01的前提下认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过0.01的前提下认为“该市居民能否做到‘光盘’与性别无关”
C.在犯错误的概率不超过0.1的前提下认为“该市居民能否做到‘光盘’与性别有关”
D.在犯错误的概率不超过0.1的前提下认为“该市居民能否做到‘光盘’与性别无关”
4.(2021·全国高二专题练)年的“金九银十”变成“铜九铁十”,全国各地房价“跳水”严重,但某地二手房交易却“逆市”而行.下图是该地某小区年月至年月间,当月在售二手房均价(单位:万元/平方米)的散点图.(图中月份代码分别对应年月年月)
根据散点图选择和两个模型进行拟合,经过数据处理得到的两个回归方程分别为和,并得到以下一些统计量的值:
注:是样本数据中的平均数,是样本数据中的平均数,则下列说法不一定成立的是( )
A.当月在售二手房均价与月份代码呈正相关关系
B.根据可以预测年月在售二手房均价约为万元/平方米
C.曲线与的图形经过点
D.回归曲线的拟合效果好于的拟合效果
5.(多选题)(2021·黄石市一中高二期末)下列关于回归分析的说法中正确的是( )
A.回归直线一定过样本中心
B.残差图中残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适
C.甲、乙两个模型的分别约为和,则模型乙的拟合效果更好
D.两个模型中残差平方和越小的模型拟合的效果越好
6.(多选题)(2021·全国高二专题练)有甲、乙两个班级共计105人进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:参考公式:
优秀 非优秀 总计
甲班 10 b
乙班 c 30
0.050 0.010 0.001
k 3.841 6.635 10.828
已知在全部105人中随机抽取1人,成绩优秀的概率为,则下列说法正确的是( )
A.列联表中c的值为30,b的值为35
B.列联表中c的值为20, b的值为45
C.根据列联表中的数据,若按95%的可靠性要求,能认为“成绩与班级有关系”
D.根据列联表中的数据,若按95%的可靠性要求,不能认为“成绩与班级有关系”
二、填空题
7.(2021·山东泰安一中高二月考)下列是关于出生男婴与女婴调查的列联表
晚上 白天 总计
男婴 45 A B
女婴 E 35 C
总计 98 D 180
那么A=________,B=________,C=________,D=________,E=________.
8.(2021·全国高二专题练) 某企业一种商品的产量与单位成本数据如下表:
产量(万件) 2 3 4
单位成本(元/件) 3 7
现根据表中所提供的数据,求得关于的线性回归直线方程为,则预测当时单位成本为每件______元.
9.(2021·福建福州三中高二月考)在吸烟与患肺癌这两个分类变量的独立性检验的计算中,下列说法正确的是________.(填序号)
①若的观测值为,在犯错误的概率不超过的前提下认为吸烟与患肺癌有关系,那么在个吸烟的人中必有人患有肺癌;
②由独立性检验可知,在犯错误的概率不超过的前提下认为吸烟与患肺癌有关系时,我们说某人吸烟,那么他有的可能患有肺癌;
③若从统计量中求出在犯错误的概率不超过的前提下认为吸烟与患肺癌有关系,是指有的可能性使得判断出现错误
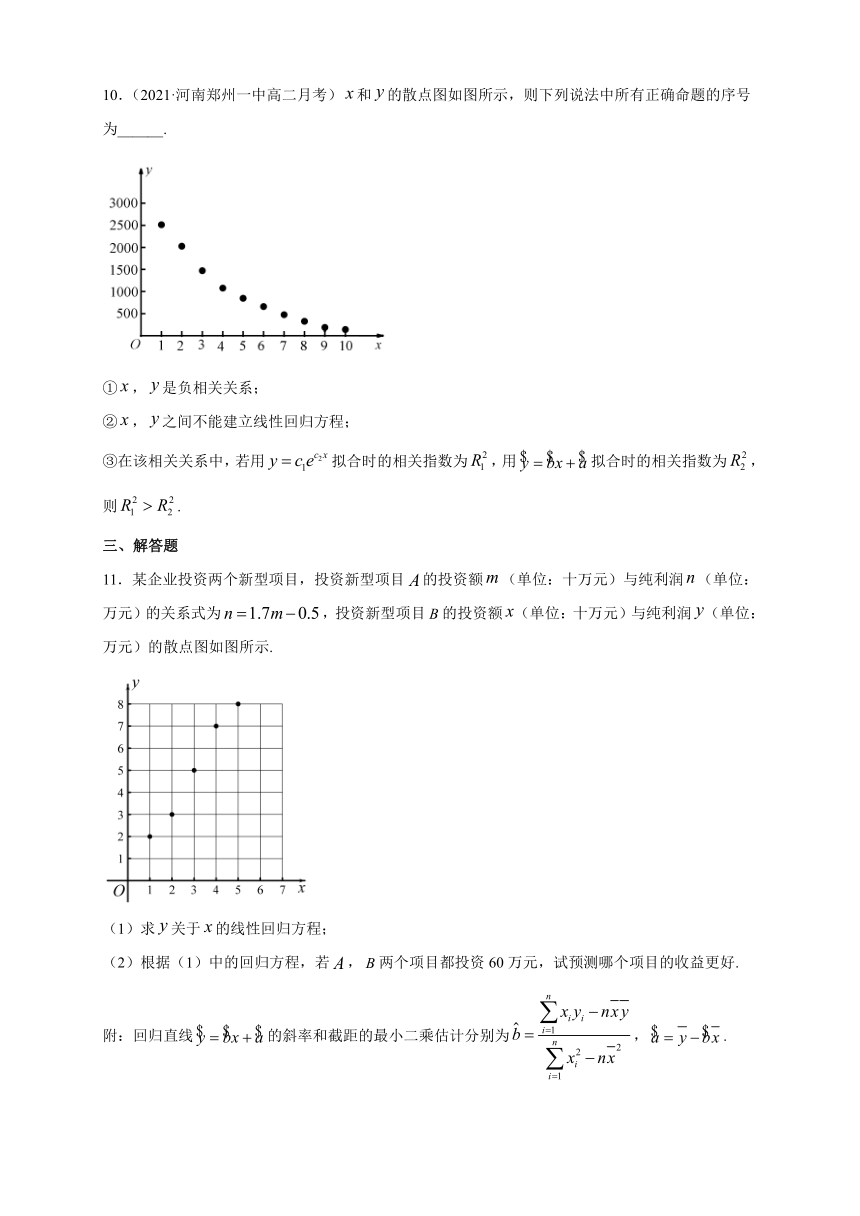
10.(2021·河南郑州一中高二月考)和的散点图如图所示,则下列说法中所有正确命题的序号为______.
①,是负相关关系;
②,之间不能建立线性回归方程;
③在该相关关系中,若用拟合时的相关指数为,用拟合时的相关指数为,则.
三、解答题
11.某企业投资两个新型项目,投资新型项目的投资额(单位:十万元)与纯利润(单位:万元)的关系式为,投资新型项目的投资额(单位:十万元)与纯利润(单位:万元)的散点图如图所示.
(1)求关于的线性回归方程;
(2)根据(1)中的回归方程,若,两个项目都投资60万元,试预测哪个项目的收益更好.
附:回归直线的斜率和截距的最小二乘估计分别为,.
12.(2021·江苏泰州市)2020年是脱贫攻坚的收官之年,国务院扶贫办确定的贫困县全部脱贫摘帽,脱贫攻坚取得重大胜利,为确保我国如期全面建成小康社会,实现第一个百年奋斗目标打下了坚实的基础在产业扶贫政策的大力支持下,西部某县新建了甲 乙两家玩具加工厂,加工同一型号的玩具质监部门随机抽检了两个厂的各100件玩具,在抽取中的200件玩具中,根据检测结果将它们分成“A” “B” “C”三个等级,A B等级都是合格品,C等级是次品,统计结果如下表所示:
等级 A B C
频数 20 120 60
(表一)
厂家 合格品 次品 合计
甲 75
乙 35
合计
(表二)
在相关政策扶持下,确保每件合格品都有对口销售渠道,但从安全起见,所有的次品必须由原厂家自行销.
(1)请根据所提供的数据,完成上面的2×2列联表(表二),并判断是否有95%的把握认为产品的合格率与厂家有关?
(2)每件玩具的生产成本为30元,A B等级产品的出厂单价分别为60元 40元.另外已知每件次品的销毁费用为4元.若甲厂抽检的玩具中有10件为A等级,用样本的频率估计概率,试判断甲 乙两厂能否都能盈利,并说明理由.
附:,其中.
0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
人教版高中数学选择性必修第三册
第八章成对数据的统计分析A卷基础训练(解析版)
一、选择题
1.(2021·全国高二课时练)某同学为了解气温对热饮销售的影响,经过统计分析,得到了一个卖出的热饮杯数与当天气温的回归方程.下列选项正确的是( )
A.与线性正相关 B.与线性负相关
C.随增大而增大 D.随减小而减小
【答案】B
【解析】由回归方程,可得:与线性负相关,且随增大而减小.
故选:B
2.(2021·全国高二课时练)如表是一个2×2列联表:则表中a,b的值分别为( )
y1 y2 合计
x1 a 21 73
x2 22 25 47
合计 b 46 120
A.94,72 B.52,50 C.52,74 D.74,52
【答案】C
【详解】a=73-21=52,b=a+22=52+22=74.故选:C.
3.(2021·无锡市才智教育培训中心高二月考)春节期间,“履行节约,反对浪费”之风悄然吹开,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:
做不到“光盘” 能做到“光盘”
男 45 10
女 30 15
附:χ2=,其中n=a+b+c+d为样本容量.
α 0.10 0.05 0.025
xα 2.706 3.841 5.024
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.01的前提下认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过0.01的前提下认为“该市居民能否做到‘光盘’与性别无关”
C.在犯错误的概率不超过0.1的前提下认为“该市居民能否做到‘光盘’与性别有关”
D.在犯错误的概率不超过0.1的前提下认为“该市居民能否做到‘光盘’与性别无关”
【答案】C
【详解】由2×2列联表得到a=45,b=10,c=30,d=15,则a+b=55,c+d=45,a+c=75,b+d=25,ad=675,bc=300,n=100,代入公式得χ2=≈3.030<3.841.
∵2.706<3.030<3.841,∴在犯错误的概率不超过0.1的前提下认为“该市居民能否做到光盘与性别有关”.
4.(2021·全国高二专题练)年的“金九银十”变成“铜九铁十”,全国各地房价“跳水”严重,但某地二手房交易却“逆市”而行.下图是该地某小区年月至年月间,当月在售二手房均价(单位:万元/平方米)的散点图.(图中月份代码分别对应年月年月)
根据散点图选择和两个模型进行拟合,经过数据处理得到的两个回归方程分别为和,并得到以下一些统计量的值:
注:是样本数据中的平均数,是样本数据中的平均数,则下列说法不一定成立的是( )
A.当月在售二手房均价与月份代码呈正相关关系
B.根据可以预测年月在售二手房均价约为万元/平方米
C.曲线与的图形经过点
D.回归曲线的拟合效果好于的拟合效果
【答案】C
【解析】对于A,散点从左下到右上分布,所以当月在售二手房均价与月份代码呈正相关关系,故A正确;对于B,令,由,所以可以预测年月在售二手房均价约为万元/平方米,故B正确;对于C,非线性回归曲线不一定经过,故C错误;对于D,越大,拟合效果越好,故D正确.故选:C.
5.(多选题)(2021·黄石市一中高二期末)下列关于回归分析的说法中正确的是( )
A.回归直线一定过样本中心
B.残差图中残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适
C.甲、乙两个模型的分别约为和,则模型乙的拟合效果更好
D.两个模型中残差平方和越小的模型拟合的效果越好
【答案】ABD
【解析】对于A选项,回归直线一定过样本中心,A选项正确;对于B选项,残差图中残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适,B选项正确;对于C选项,甲、乙两个模型的分别约为和,则模型甲的拟合效果更好,C选项错误;对于D选项,两个模型中残差平方和越小的模型拟合的效果越好,D选项正确.故选:ABD.
6.(多选题)(2021·全国高二专题练)有甲、乙两个班级共计105人进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:参考公式:
优秀 非优秀 总计
甲班 10 b
乙班 c 30
0.050 0.010 0.001
k 3.841 6.635 10.828
已知在全部105人中随机抽取1人,成绩优秀的概率为,则下列说法正确的是( )
A.列联表中c的值为30,b的值为35
B.列联表中c的值为20, b的值为45
C.根据列联表中的数据,若按95%的可靠性要求,能认为“成绩与班级有关系”
D.根据列联表中的数据,若按95%的可靠性要求,不能认为“成绩与班级有关系”
【答案】BC
【详解】由题意,在全部的105人中随机抽取1人,成绩优秀的概率为,所以成绩又由的人数为人,非优秀的人数为人,所以,
则,若按95%的可靠性要求,能认为“成绩与班级有关系”.故选:BC.
二、填空题
7.(2021·山东泰安一中高二月考)下列是关于出生男婴与女婴调查的列联表
晚上 白天 总计
男婴 45 A B
女婴 E 35 C
总计 98 D 180
那么A=________,B=________,C=________,D=________,E=________.
【答案】47; 92; 88; 82; 53
【详解】∵45+E=98,∴E=53,∵E+35=C,∴C=88,∵98+D=180,∴D=82,
∵A+35=D,∴A=47,∵45+A=B,∴B=92.
8.(2021·全国高二专题练) 某企业一种商品的产量与单位成本数据如下表:
产量(万件) 2 3 4
单位成本(元/件) 3 7
现根据表中所提供的数据,求得关于的线性回归直线方程为,则预测当时单位成本为每件______元.
【答案】9
【详解】由所给数据可求得,,代入线性回归直线方程,得,解得,所以线性回归直线方程,当时单位成本(元/件).
9.(2021·福建福州三中高二月考)在吸烟与患肺癌这两个分类变量的独立性检验的计算中,下列说法正确的是________.(填序号)
①若的观测值为,在犯错误的概率不超过的前提下认为吸烟与患肺癌有关系,那么在个吸烟的人中必有人患有肺癌;
②由独立性检验可知,在犯错误的概率不超过的前提下认为吸烟与患肺癌有关系时,我们说某人吸烟,那么他有的可能患有肺癌;
③若从统计量中求出在犯错误的概率不超过的前提下认为吸烟与患肺癌有关系,是指有的可能性使得判断出现错误
【答案】③
【解析】若从统计量中求出在犯错误的概率不超过的前提下认为吸烟与患肺癌有关系,是指有的可能性使得判断出现错误,故③正确.
10.(2021·河南郑州一中高二月考)和的散点图如图所示,则下列说法中所有正确命题的序号为______.
①,是负相关关系;
②,之间不能建立线性回归方程;
③在该相关关系中,若用拟合时的相关指数为,用拟合时的相关指数为,则.
【答案】①③
【详解】在散点图中,点散布在从左上角到右下角的区域,因此,是负相关关系,故①正确;
x,,y之间可以建立线性回归方程,但拟合效果不好,故②错误;
由散点图知用拟合比用拟合效果要好,则,故③正确.
三、解答题
11.某企业投资两个新型项目,投资新型项目的投资额(单位:十万元)与纯利润(单位:万元)的关系式为,投资新型项目的投资额(单位:十万元)与纯利润(单位:万元)的散点图如图所示.
(1)求关于的线性回归方程;
(2)根据(1)中的回归方程,若,两个项目都投资60万元,试预测哪个项目的收益更好.
附:回归直线的斜率和截距的最小二乘估计分别为,.
【答案】(1);(2)项目的收益更好.
【解析】(1)由散点图可知,取时,的值分别为,
所以,,
,
则,
故关于的线性回归方程为.
(2)因为投资新型项目的投资额(单位:十万元)与纯利润(单位:万元)的关系式为,
所以若项目投资60万元,则该企业所得纯利润的估计值为万元;
因为关于的线性回归方程为,
所以若项目投资60万元,则该企业所得纯利润的估计值为万元.
因为,所以可预测项目的收益更好.
12.(2021·江苏泰州市)2020年是脱贫攻坚的收官之年,国务院扶贫办确定的贫困县全部脱贫摘帽,脱贫攻坚取得重大胜利,为确保我国如期全面建成小康社会,实现第一个百年奋斗目标打下了坚实的基础在产业扶贫政策的大力支持下,西部某县新建了甲 乙两家玩具加工厂,加工同一型号的玩具质监部门随机抽检了两个厂的各100件玩具,在抽取中的200件玩具中,根据检测结果将它们分成“A” “B” “C”三个等级,A B等级都是合格品,C等级是次品,统计结果如下表所示:
等级 A B C
频数 20 120 60
(表一)
厂家 合格品 次品 合计
甲 75
乙 35
合计
(表二)
在相关政策扶持下,确保每件合格品都有对口销售渠道,但从安全起见,所有的次品必须由原厂家自行销.
(1)请根据所提供的数据,完成上面的2×2列联表(表二),并判断是否有95%的把握认为产品的合格率与厂家有关?
(2)每件玩具的生产成本为30元,A B等级产品的出厂单价分别为60元 40元.另外已知每件次品的销毁费用为4元.若甲厂抽检的玩具中有10件为A等级,用样本的频率估计概率,试判断甲 乙两厂能否都能盈利,并说明理由.
附:,其中.
0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
【答案】(1)列联表答案见解析,没有95%的把握认为产品的合格率与厂家有关;(2)甲厂能盈利,乙不能盈利,理由见解析.
【解析】(1)2×2列联表如下
厂家 合格品 次品 合计
甲 75 25 100
乙 65 35 100
合计 140 60 200
,
没有95%的把握认为产品的合格率与厂家有关.
(2)甲厂10件A等级,65件B等级,25件次品,
对于甲厂,单件产品利润X的可能取值为30,10,.
X的分布列如下:
X 30 10
P
,
甲厂能盈利,
对于乙厂有10件A等级,55件B等级,35件次品,
对于乙厂,单位产品利润Y的可能取值为30,10,,
Y分布列如下:
Y 30 10
P
,乙不能盈利.
联系QQ309000116加入百度网盘群3500G一线老师必备资料一键转存,自动更新,一劳永逸
人教版高中数学选择性必修第三册
第八章成对数据的统计分析A卷基础训练(原卷版)
一、选择题
1.(2021·全国高二课时练)某同学为了解气温对热饮销售的影响,经过统计分析,得到了一个卖出的热饮杯数与当天气温的回归方程.下列选项正确的是( )
A.与线性正相关 B.与线性负相关
C.随增大而增大 D.随减小而减小
2.(2021·全国高二课时练)如表是一个2×2列联表:则表中a,b的值分别为( )
y1 y2 合计
x1 a 21 73
x2 22 25 47
合计 b 46 120
A.94,72 B.52,50 C.52,74 D.74,52
3.(2021·无锡市才智教育培训中心高二月考)春节期间,“履行节约,反对浪费”之风悄然吹开,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:
做不到“光盘” 能做到“光盘”
男 45 10
女 30 15
附:χ2=,其中n=a+b+c+d为样本容量.
α 0.10 0.05 0.025
xα 2.706 3.841 5.024
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.01的前提下认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过0.01的前提下认为“该市居民能否做到‘光盘’与性别无关”
C.在犯错误的概率不超过0.1的前提下认为“该市居民能否做到‘光盘’与性别有关”
D.在犯错误的概率不超过0.1的前提下认为“该市居民能否做到‘光盘’与性别无关”
4.(2021·全国高二专题练)年的“金九银十”变成“铜九铁十”,全国各地房价“跳水”严重,但某地二手房交易却“逆市”而行.下图是该地某小区年月至年月间,当月在售二手房均价(单位:万元/平方米)的散点图.(图中月份代码分别对应年月年月)
根据散点图选择和两个模型进行拟合,经过数据处理得到的两个回归方程分别为和,并得到以下一些统计量的值:
注:是样本数据中的平均数,是样本数据中的平均数,则下列说法不一定成立的是( )
A.当月在售二手房均价与月份代码呈正相关关系
B.根据可以预测年月在售二手房均价约为万元/平方米
C.曲线与的图形经过点
D.回归曲线的拟合效果好于的拟合效果
5.(多选题)(2021·黄石市一中高二期末)下列关于回归分析的说法中正确的是( )
A.回归直线一定过样本中心
B.残差图中残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适
C.甲、乙两个模型的分别约为和,则模型乙的拟合效果更好
D.两个模型中残差平方和越小的模型拟合的效果越好
6.(多选题)(2021·全国高二专题练)有甲、乙两个班级共计105人进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:参考公式:
优秀 非优秀 总计
甲班 10 b
乙班 c 30
0.050 0.010 0.001
k 3.841 6.635 10.828
已知在全部105人中随机抽取1人,成绩优秀的概率为,则下列说法正确的是( )
A.列联表中c的值为30,b的值为35
B.列联表中c的值为20, b的值为45
C.根据列联表中的数据,若按95%的可靠性要求,能认为“成绩与班级有关系”
D.根据列联表中的数据,若按95%的可靠性要求,不能认为“成绩与班级有关系”
二、填空题
7.(2021·山东泰安一中高二月考)下列是关于出生男婴与女婴调查的列联表
晚上 白天 总计
男婴 45 A B
女婴 E 35 C
总计 98 D 180
那么A=________,B=________,C=________,D=________,E=________.
8.(2021·全国高二专题练) 某企业一种商品的产量与单位成本数据如下表:
产量(万件) 2 3 4
单位成本(元/件) 3 7
现根据表中所提供的数据,求得关于的线性回归直线方程为,则预测当时单位成本为每件______元.
9.(2021·福建福州三中高二月考)在吸烟与患肺癌这两个分类变量的独立性检验的计算中,下列说法正确的是________.(填序号)
①若的观测值为,在犯错误的概率不超过的前提下认为吸烟与患肺癌有关系,那么在个吸烟的人中必有人患有肺癌;
②由独立性检验可知,在犯错误的概率不超过的前提下认为吸烟与患肺癌有关系时,我们说某人吸烟,那么他有的可能患有肺癌;
③若从统计量中求出在犯错误的概率不超过的前提下认为吸烟与患肺癌有关系,是指有的可能性使得判断出现错误
10.(2021·河南郑州一中高二月考)和的散点图如图所示,则下列说法中所有正确命题的序号为______.
①,是负相关关系;
②,之间不能建立线性回归方程;
③在该相关关系中,若用拟合时的相关指数为,用拟合时的相关指数为,则.
三、解答题
11.某企业投资两个新型项目,投资新型项目的投资额(单位:十万元)与纯利润(单位:万元)的关系式为,投资新型项目的投资额(单位:十万元)与纯利润(单位:万元)的散点图如图所示.
(1)求关于的线性回归方程;
(2)根据(1)中的回归方程,若,两个项目都投资60万元,试预测哪个项目的收益更好.
附:回归直线的斜率和截距的最小二乘估计分别为,.
12.(2021·江苏泰州市)2020年是脱贫攻坚的收官之年,国务院扶贫办确定的贫困县全部脱贫摘帽,脱贫攻坚取得重大胜利,为确保我国如期全面建成小康社会,实现第一个百年奋斗目标打下了坚实的基础在产业扶贫政策的大力支持下,西部某县新建了甲 乙两家玩具加工厂,加工同一型号的玩具质监部门随机抽检了两个厂的各100件玩具,在抽取中的200件玩具中,根据检测结果将它们分成“A” “B” “C”三个等级,A B等级都是合格品,C等级是次品,统计结果如下表所示:
等级 A B C
频数 20 120 60
(表一)
厂家 合格品 次品 合计
甲 75
乙 35
合计
(表二)
在相关政策扶持下,确保每件合格品都有对口销售渠道,但从安全起见,所有的次品必须由原厂家自行销.
(1)请根据所提供的数据,完成上面的2×2列联表(表二),并判断是否有95%的把握认为产品的合格率与厂家有关?
(2)每件玩具的生产成本为30元,A B等级产品的出厂单价分别为60元 40元.另外已知每件次品的销毁费用为4元.若甲厂抽检的玩具中有10件为A等级,用样本的频率估计概率,试判断甲 乙两厂能否都能盈利,并说明理由.
附:,其中.
0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
人教版高中数学选择性必修第三册
第八章成对数据的统计分析A卷基础训练(解析版)
一、选择题
1.(2021·全国高二课时练)某同学为了解气温对热饮销售的影响,经过统计分析,得到了一个卖出的热饮杯数与当天气温的回归方程.下列选项正确的是( )
A.与线性正相关 B.与线性负相关
C.随增大而增大 D.随减小而减小
【答案】B
【解析】由回归方程,可得:与线性负相关,且随增大而减小.
故选:B
2.(2021·全国高二课时练)如表是一个2×2列联表:则表中a,b的值分别为( )
y1 y2 合计
x1 a 21 73
x2 22 25 47
合计 b 46 120
A.94,72 B.52,50 C.52,74 D.74,52
【答案】C
【详解】a=73-21=52,b=a+22=52+22=74.故选:C.
3.(2021·无锡市才智教育培训中心高二月考)春节期间,“履行节约,反对浪费”之风悄然吹开,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:
做不到“光盘” 能做到“光盘”
男 45 10
女 30 15
附:χ2=,其中n=a+b+c+d为样本容量.
α 0.10 0.05 0.025
xα 2.706 3.841 5.024
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.01的前提下认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过0.01的前提下认为“该市居民能否做到‘光盘’与性别无关”
C.在犯错误的概率不超过0.1的前提下认为“该市居民能否做到‘光盘’与性别有关”
D.在犯错误的概率不超过0.1的前提下认为“该市居民能否做到‘光盘’与性别无关”
【答案】C
【详解】由2×2列联表得到a=45,b=10,c=30,d=15,则a+b=55,c+d=45,a+c=75,b+d=25,ad=675,bc=300,n=100,代入公式得χ2=≈3.030<3.841.
∵2.706<3.030<3.841,∴在犯错误的概率不超过0.1的前提下认为“该市居民能否做到光盘与性别有关”.
4.(2021·全国高二专题练)年的“金九银十”变成“铜九铁十”,全国各地房价“跳水”严重,但某地二手房交易却“逆市”而行.下图是该地某小区年月至年月间,当月在售二手房均价(单位:万元/平方米)的散点图.(图中月份代码分别对应年月年月)
根据散点图选择和两个模型进行拟合,经过数据处理得到的两个回归方程分别为和,并得到以下一些统计量的值:
注:是样本数据中的平均数,是样本数据中的平均数,则下列说法不一定成立的是( )
A.当月在售二手房均价与月份代码呈正相关关系
B.根据可以预测年月在售二手房均价约为万元/平方米
C.曲线与的图形经过点
D.回归曲线的拟合效果好于的拟合效果
【答案】C
【解析】对于A,散点从左下到右上分布,所以当月在售二手房均价与月份代码呈正相关关系,故A正确;对于B,令,由,所以可以预测年月在售二手房均价约为万元/平方米,故B正确;对于C,非线性回归曲线不一定经过,故C错误;对于D,越大,拟合效果越好,故D正确.故选:C.
5.(多选题)(2021·黄石市一中高二期末)下列关于回归分析的说法中正确的是( )
A.回归直线一定过样本中心
B.残差图中残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适
C.甲、乙两个模型的分别约为和,则模型乙的拟合效果更好
D.两个模型中残差平方和越小的模型拟合的效果越好
【答案】ABD
【解析】对于A选项,回归直线一定过样本中心,A选项正确;对于B选项,残差图中残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适,B选项正确;对于C选项,甲、乙两个模型的分别约为和,则模型甲的拟合效果更好,C选项错误;对于D选项,两个模型中残差平方和越小的模型拟合的效果越好,D选项正确.故选:ABD.
6.(多选题)(2021·全国高二专题练)有甲、乙两个班级共计105人进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:参考公式:
优秀 非优秀 总计
甲班 10 b
乙班 c 30
0.050 0.010 0.001
k 3.841 6.635 10.828
已知在全部105人中随机抽取1人,成绩优秀的概率为,则下列说法正确的是( )
A.列联表中c的值为30,b的值为35
B.列联表中c的值为20, b的值为45
C.根据列联表中的数据,若按95%的可靠性要求,能认为“成绩与班级有关系”
D.根据列联表中的数据,若按95%的可靠性要求,不能认为“成绩与班级有关系”
【答案】BC
【详解】由题意,在全部的105人中随机抽取1人,成绩优秀的概率为,所以成绩又由的人数为人,非优秀的人数为人,所以,
则,若按95%的可靠性要求,能认为“成绩与班级有关系”.故选:BC.
二、填空题
7.(2021·山东泰安一中高二月考)下列是关于出生男婴与女婴调查的列联表
晚上 白天 总计
男婴 45 A B
女婴 E 35 C
总计 98 D 180
那么A=________,B=________,C=________,D=________,E=________.
【答案】47; 92; 88; 82; 53
【详解】∵45+E=98,∴E=53,∵E+35=C,∴C=88,∵98+D=180,∴D=82,
∵A+35=D,∴A=47,∵45+A=B,∴B=92.
8.(2021·全国高二专题练) 某企业一种商品的产量与单位成本数据如下表:
产量(万件) 2 3 4
单位成本(元/件) 3 7
现根据表中所提供的数据,求得关于的线性回归直线方程为,则预测当时单位成本为每件______元.
【答案】9
【详解】由所给数据可求得,,代入线性回归直线方程,得,解得,所以线性回归直线方程,当时单位成本(元/件).
9.(2021·福建福州三中高二月考)在吸烟与患肺癌这两个分类变量的独立性检验的计算中,下列说法正确的是________.(填序号)
①若的观测值为,在犯错误的概率不超过的前提下认为吸烟与患肺癌有关系,那么在个吸烟的人中必有人患有肺癌;
②由独立性检验可知,在犯错误的概率不超过的前提下认为吸烟与患肺癌有关系时,我们说某人吸烟,那么他有的可能患有肺癌;
③若从统计量中求出在犯错误的概率不超过的前提下认为吸烟与患肺癌有关系,是指有的可能性使得判断出现错误
【答案】③
【解析】若从统计量中求出在犯错误的概率不超过的前提下认为吸烟与患肺癌有关系,是指有的可能性使得判断出现错误,故③正确.
10.(2021·河南郑州一中高二月考)和的散点图如图所示,则下列说法中所有正确命题的序号为______.
①,是负相关关系;
②,之间不能建立线性回归方程;
③在该相关关系中,若用拟合时的相关指数为,用拟合时的相关指数为,则.
【答案】①③
【详解】在散点图中,点散布在从左上角到右下角的区域,因此,是负相关关系,故①正确;
x,,y之间可以建立线性回归方程,但拟合效果不好,故②错误;
由散点图知用拟合比用拟合效果要好,则,故③正确.
三、解答题
11.某企业投资两个新型项目,投资新型项目的投资额(单位:十万元)与纯利润(单位:万元)的关系式为,投资新型项目的投资额(单位:十万元)与纯利润(单位:万元)的散点图如图所示.
(1)求关于的线性回归方程;
(2)根据(1)中的回归方程,若,两个项目都投资60万元,试预测哪个项目的收益更好.
附:回归直线的斜率和截距的最小二乘估计分别为,.
【答案】(1);(2)项目的收益更好.
【解析】(1)由散点图可知,取时,的值分别为,
所以,,
,
则,
故关于的线性回归方程为.
(2)因为投资新型项目的投资额(单位:十万元)与纯利润(单位:万元)的关系式为,
所以若项目投资60万元,则该企业所得纯利润的估计值为万元;
因为关于的线性回归方程为,
所以若项目投资60万元,则该企业所得纯利润的估计值为万元.
因为,所以可预测项目的收益更好.
12.(2021·江苏泰州市)2020年是脱贫攻坚的收官之年,国务院扶贫办确定的贫困县全部脱贫摘帽,脱贫攻坚取得重大胜利,为确保我国如期全面建成小康社会,实现第一个百年奋斗目标打下了坚实的基础在产业扶贫政策的大力支持下,西部某县新建了甲 乙两家玩具加工厂,加工同一型号的玩具质监部门随机抽检了两个厂的各100件玩具,在抽取中的200件玩具中,根据检测结果将它们分成“A” “B” “C”三个等级,A B等级都是合格品,C等级是次品,统计结果如下表所示:
等级 A B C
频数 20 120 60
(表一)
厂家 合格品 次品 合计
甲 75
乙 35
合计
(表二)
在相关政策扶持下,确保每件合格品都有对口销售渠道,但从安全起见,所有的次品必须由原厂家自行销.
(1)请根据所提供的数据,完成上面的2×2列联表(表二),并判断是否有95%的把握认为产品的合格率与厂家有关?
(2)每件玩具的生产成本为30元,A B等级产品的出厂单价分别为60元 40元.另外已知每件次品的销毁费用为4元.若甲厂抽检的玩具中有10件为A等级,用样本的频率估计概率,试判断甲 乙两厂能否都能盈利,并说明理由.
附:,其中.
0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
【答案】(1)列联表答案见解析,没有95%的把握认为产品的合格率与厂家有关;(2)甲厂能盈利,乙不能盈利,理由见解析.
【解析】(1)2×2列联表如下
厂家 合格品 次品 合计
甲 75 25 100
乙 65 35 100
合计 140 60 200
,
没有95%的把握认为产品的合格率与厂家有关.
(2)甲厂10件A等级,65件B等级,25件次品,
对于甲厂,单件产品利润X的可能取值为30,10,.
X的分布列如下:
X 30 10
P
,
甲厂能盈利,
对于乙厂有10件A等级,55件B等级,35件次品,
对于乙厂,单位产品利润Y的可能取值为30,10,,
Y分布列如下:
Y 30 10
P
,乙不能盈利.
联系QQ309000116加入百度网盘群3500G一线老师必备资料一键转存,自动更新,一劳永逸
