《圆柱的表面积》(课件)-六年级下册数学苏教版(共33张PPT)
文档属性
| 名称 | 《圆柱的表面积》(课件)-六年级下册数学苏教版(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 261.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-11 10:12:06 | ||
图片预览






文档简介
(共33张PPT)
苏教版小学数学六年级下册
圆柱的表面积
有正方体(棱长10厘米)、长方体(长10厘米、宽8厘米、高10厘米)、圆柱(底面直径10厘米,高10厘米)形状的三个包装盒,如果要在每个包装盒的四周贴一圈装饰纸,分别需要装饰纸多少平方厘米?
情境导入
预习展示
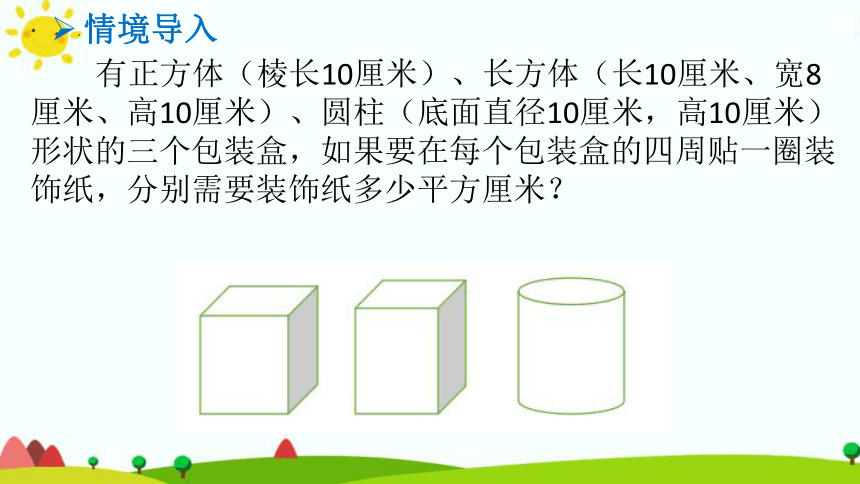
动手操作:将圆柱侧面沿高剪开
(一)探究圆柱侧面积公式:
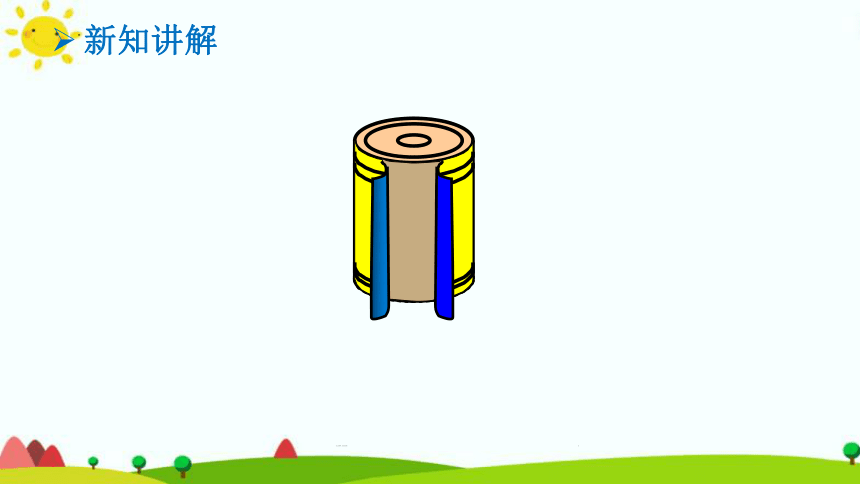
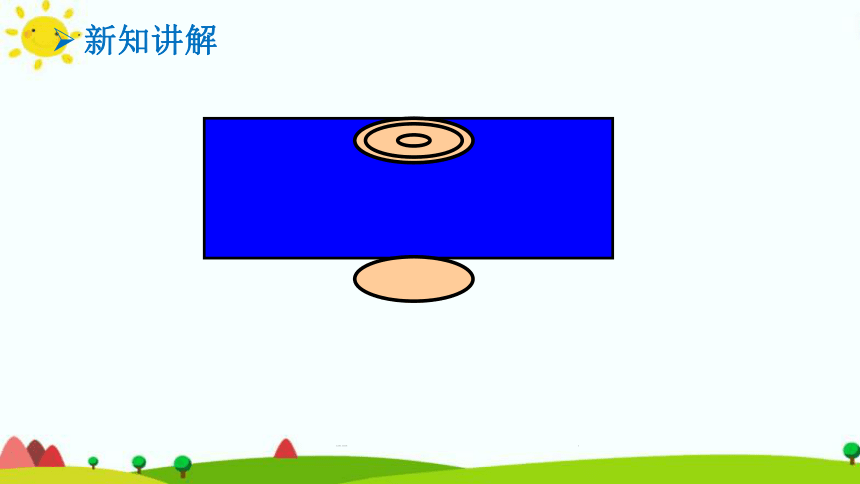
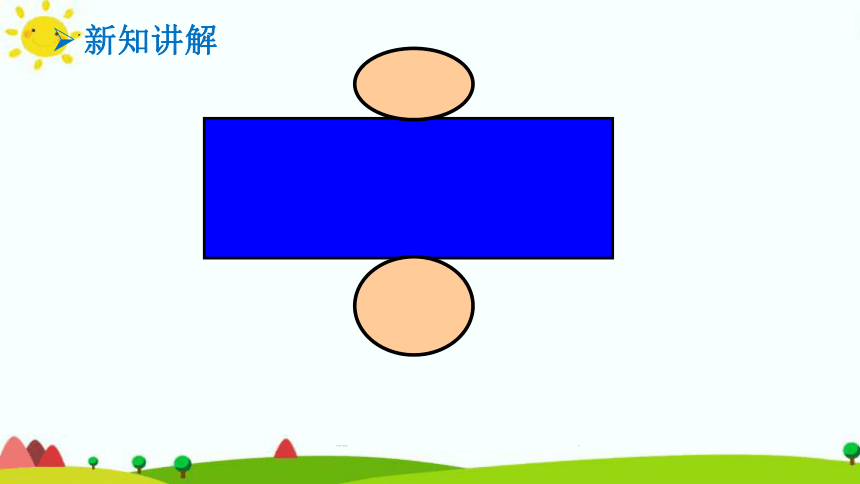
1.展开后是什么形状?( )
2.长方形的长和宽与圆柱有什么关系?
长:圆柱的( )
因为:圆柱侧面展开 长方形
宽:圆柱的( )
又因为:长方形面积 = 长 × 宽
所以 :圆柱侧面积 =( ),字母表示是( )。
长方形
底面周长
高
底面周长×高
S侧 = ch
活动要求
1.小组合作:拿出圆柱形模型,用剪刀沿接缝处剪开。
2.小组交流:(1)圆柱展开后是什么形状?
(2)这个长方形的长和宽与圆柱有什么关系?
(3)怎样计算圆柱的侧面积?
(观察、比较、推理、总结)
3.小组汇报:组内成员上台展示
小组合作交流
优秀课件,精彩无限!
5
一个圆柱形状的罐头,它的底面直径是11厘米,高是15厘米。侧面有一张商标纸,商标纸的面积大约是多少平方厘米? (接头处忽略不计)
新知讲解
优秀课件,精彩无限!
6
新知讲解
优秀课件,精彩无限!
7
新知讲解
优秀课件,精彩无限!
8
新知讲解
优秀课件,精彩无限!
9
新知讲解
优秀课件,精彩无限!
10
新知讲解
优秀课件,精彩无限!
11
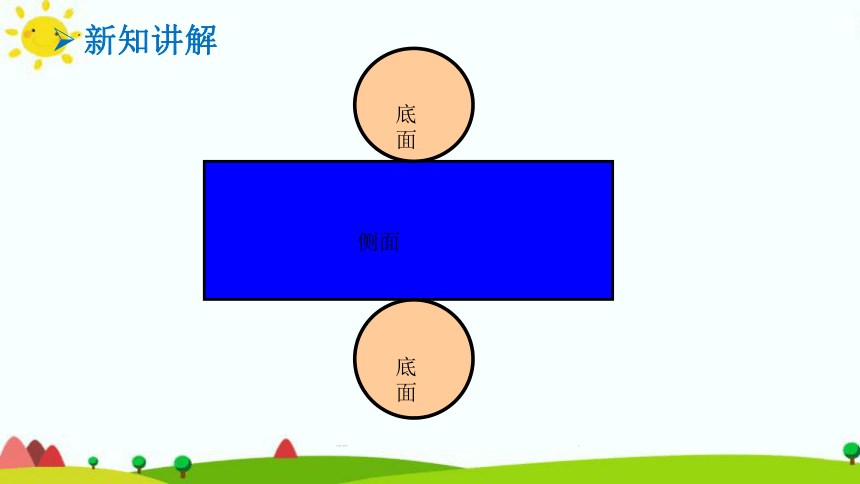
底面
底面
侧面
新知讲解
优秀课件,精彩无限!
12
底面
底面
侧面
新知讲解
优秀课件,精彩无限!
13
底面
底面
侧面
新知讲解
优秀课件,精彩无限!
14
底面
底面
侧面
新知讲解
优秀课件,精彩无限!
15
底面
底面
侧面
新知讲解
优秀课件,精彩无限!
16
底面
底面
侧面
新知讲解
优秀课件,精彩无限!
17
底面
底面
侧面
新知讲解
优秀课件,精彩无限!
18
底面
底面
侧面
新知讲解
优秀课件,精彩无限!
19
底面
底面
侧面
新知讲解
优秀课件,精彩无限!
20
底面
底面
侧面
新知讲解
优秀课件,精彩无限!
21
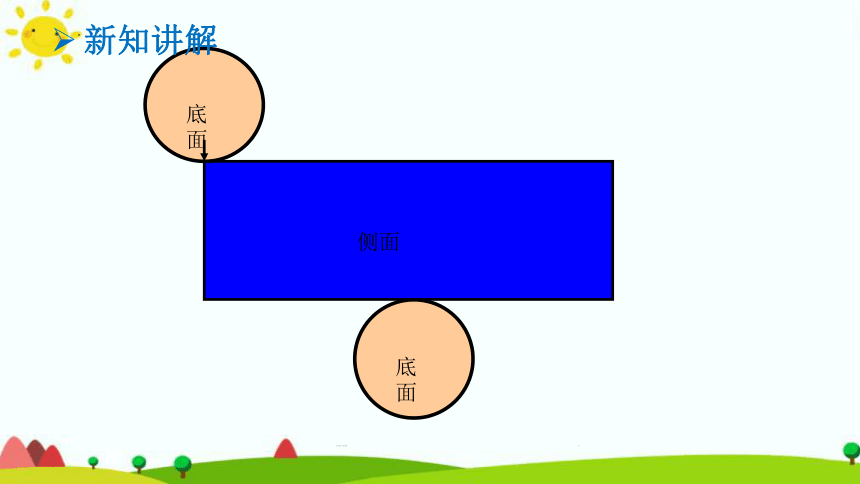
底面的周长
底面
高
底面
1.沿着接缝把商标纸剪开展开后是什么形状?
2.这个长方形的长和宽与圆柱有什么关系?
3.怎样计算圆柱的侧面积?
把你的发现告诉同组的同学。
侧面
新知讲解
优秀课件,精彩无限!
22
新知讲解
长方形的面积 = 长 × 宽
圆柱的侧面积 = 底面周长×高
S侧=ch
优秀课件,精彩无限!
23
一个圆柱形状的罐头,它的底面直径是11厘米,高是15厘米。侧面有一张商标纸,商标纸的面积大约是多少平方厘米?(接头处忽略不计)
S侧=πdh
=11π×15
=165π
提示:像这样先写公式,再代数字,最后的计算结果不写单位。
答:商标纸的面积大约是165π平方厘米。
新知应用
优秀课件,精彩无限!
24
6
一个圆柱(如右图),底面周长是31.4厘米,高是6厘米。求它的侧面积。
6
S侧=ch
=31.4×6
=188.4
答:它的侧面积是188.4平方厘米。
新知应用
预习展示
1.完成课本12页例3。(把右边圆柱的侧面沿高展开,得到的长方形的长和宽各是多少厘米?圆柱的底面半径是多少厘米 请在方格纸上画出这个圆柱的展开图。再算出圆柱的表面积)
长:2π厘米
宽:2厘米
底面半径:2÷2=1(厘米)
c=πd
=2π
2πcm
2cm
2cm
2cm
侧面积:2π×2=4π(cm )
2个底面积:2×π×1 =2π(cm )
表面积:4π+2π=6π(cm )
优秀课件,精彩无限!
26
圆柱的侧面积与两个底面积的和,叫做圆柱的表面积。
即: (圆柱的表面积=侧面积+2个底面积)
预习展示
优秀课件,精彩无限!
27
底面周长×高
圆柱的侧面积 + 两个底面的面积
圆柱的表面积=
S表面积=2πr×h + 2×πr2
侧面
底面
底面
新知讲解
优秀课件,精彩无限!
28
1.计算下面各圆柱的表面积.(单位:cm)
0.8
22
3.5
0.5
2
0.5
3.5
新知应用
2.完成课本13页第4题。少先队队鼓是圆柱形的,侧面由铝皮围成,上下底面蒙的是羊皮。做这样一个队鼓,至少需要铝皮多少平方分米?羊皮呢?
答:至少需要铝皮15.6π平方分米;羊皮18π平方分米。
铝皮:S侧=πdh
=6π×2.6
=15.6π
羊皮:2S底=2πr
=2π×(6÷2)
= 18π
新知应用
3.一个圆柱形油桶,底面直径是0.6米,高是1米。做这个油桶至少需要铁皮多少平方米?(得数保留两位小数)
答:做这个油桶至少需要铁皮2.45平方米。
S侧=πdh
=0.6π×1
=0.6π
2S底=2πr
=2π×(0.6÷2)
=2π×0.3
= 0.18π
S表=S侧+2S底
=0.6π+0.18π
=0.78π
=2.4492
≈2.45
新知应用
优秀课件,精彩无限!
31
拓展延伸
对于这两个立体图形的侧面积和表面积,你有什么想说的?你还能想到什么?大家可以利用课余时间去继续研究,并把研究的结果写下来,与同学交流。
这堂课我们学习了什么
怎样求圆柱的表面积
你想提醒大家注意什么
全课总结
谢 谢
苏教版小学数学六年级下册
圆柱的表面积
有正方体(棱长10厘米)、长方体(长10厘米、宽8厘米、高10厘米)、圆柱(底面直径10厘米,高10厘米)形状的三个包装盒,如果要在每个包装盒的四周贴一圈装饰纸,分别需要装饰纸多少平方厘米?
情境导入
预习展示
动手操作:将圆柱侧面沿高剪开
(一)探究圆柱侧面积公式:
1.展开后是什么形状?( )
2.长方形的长和宽与圆柱有什么关系?
长:圆柱的( )
因为:圆柱侧面展开 长方形
宽:圆柱的( )
又因为:长方形面积 = 长 × 宽
所以 :圆柱侧面积 =( ),字母表示是( )。
长方形
底面周长
高
底面周长×高
S侧 = ch
活动要求
1.小组合作:拿出圆柱形模型,用剪刀沿接缝处剪开。
2.小组交流:(1)圆柱展开后是什么形状?
(2)这个长方形的长和宽与圆柱有什么关系?
(3)怎样计算圆柱的侧面积?
(观察、比较、推理、总结)
3.小组汇报:组内成员上台展示
小组合作交流
优秀课件,精彩无限!
5
一个圆柱形状的罐头,它的底面直径是11厘米,高是15厘米。侧面有一张商标纸,商标纸的面积大约是多少平方厘米? (接头处忽略不计)
新知讲解
优秀课件,精彩无限!
6
新知讲解
优秀课件,精彩无限!
7
新知讲解
优秀课件,精彩无限!
8
新知讲解
优秀课件,精彩无限!
9
新知讲解
优秀课件,精彩无限!
10
新知讲解
优秀课件,精彩无限!
11
底面
底面
侧面
新知讲解
优秀课件,精彩无限!
12
底面
底面
侧面
新知讲解
优秀课件,精彩无限!
13
底面
底面
侧面
新知讲解
优秀课件,精彩无限!
14
底面
底面
侧面
新知讲解
优秀课件,精彩无限!
15
底面
底面
侧面
新知讲解
优秀课件,精彩无限!
16
底面
底面
侧面
新知讲解
优秀课件,精彩无限!
17
底面
底面
侧面
新知讲解
优秀课件,精彩无限!
18
底面
底面
侧面
新知讲解
优秀课件,精彩无限!
19
底面
底面
侧面
新知讲解
优秀课件,精彩无限!
20
底面
底面
侧面
新知讲解
优秀课件,精彩无限!
21
底面的周长
底面
高
底面
1.沿着接缝把商标纸剪开展开后是什么形状?
2.这个长方形的长和宽与圆柱有什么关系?
3.怎样计算圆柱的侧面积?
把你的发现告诉同组的同学。
侧面
新知讲解
优秀课件,精彩无限!
22
新知讲解
长方形的面积 = 长 × 宽
圆柱的侧面积 = 底面周长×高
S侧=ch
优秀课件,精彩无限!
23
一个圆柱形状的罐头,它的底面直径是11厘米,高是15厘米。侧面有一张商标纸,商标纸的面积大约是多少平方厘米?(接头处忽略不计)
S侧=πdh
=11π×15
=165π
提示:像这样先写公式,再代数字,最后的计算结果不写单位。
答:商标纸的面积大约是165π平方厘米。
新知应用
优秀课件,精彩无限!
24
6
一个圆柱(如右图),底面周长是31.4厘米,高是6厘米。求它的侧面积。
6
S侧=ch
=31.4×6
=188.4
答:它的侧面积是188.4平方厘米。
新知应用
预习展示
1.完成课本12页例3。(把右边圆柱的侧面沿高展开,得到的长方形的长和宽各是多少厘米?圆柱的底面半径是多少厘米 请在方格纸上画出这个圆柱的展开图。再算出圆柱的表面积)
长:2π厘米
宽:2厘米
底面半径:2÷2=1(厘米)
c=πd
=2π
2πcm
2cm
2cm
2cm
侧面积:2π×2=4π(cm )
2个底面积:2×π×1 =2π(cm )
表面积:4π+2π=6π(cm )
优秀课件,精彩无限!
26
圆柱的侧面积与两个底面积的和,叫做圆柱的表面积。
即: (圆柱的表面积=侧面积+2个底面积)
预习展示
优秀课件,精彩无限!
27
底面周长×高
圆柱的侧面积 + 两个底面的面积
圆柱的表面积=
S表面积=2πr×h + 2×πr2
侧面
底面
底面
新知讲解
优秀课件,精彩无限!
28
1.计算下面各圆柱的表面积.(单位:cm)
0.8
22
3.5
0.5
2
0.5
3.5
新知应用
2.完成课本13页第4题。少先队队鼓是圆柱形的,侧面由铝皮围成,上下底面蒙的是羊皮。做这样一个队鼓,至少需要铝皮多少平方分米?羊皮呢?
答:至少需要铝皮15.6π平方分米;羊皮18π平方分米。
铝皮:S侧=πdh
=6π×2.6
=15.6π
羊皮:2S底=2πr
=2π×(6÷2)
= 18π
新知应用
3.一个圆柱形油桶,底面直径是0.6米,高是1米。做这个油桶至少需要铁皮多少平方米?(得数保留两位小数)
答:做这个油桶至少需要铁皮2.45平方米。
S侧=πdh
=0.6π×1
=0.6π
2S底=2πr
=2π×(0.6÷2)
=2π×0.3
= 0.18π
S表=S侧+2S底
=0.6π+0.18π
=0.78π
=2.4492
≈2.45
新知应用
优秀课件,精彩无限!
31
拓展延伸
对于这两个立体图形的侧面积和表面积,你有什么想说的?你还能想到什么?大家可以利用课余时间去继续研究,并把研究的结果写下来,与同学交流。
这堂课我们学习了什么
怎样求圆柱的表面积
你想提醒大家注意什么
全课总结
谢 谢
