4.1.2 等式的基本性质同步练习(含答案)
文档属性
| 名称 | 4.1.2 等式的基本性质同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-11 20:12:27 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第四章 一元一次方程
1 等式与方程
第2课时 等式的基本性质
夯实基础逐点练习
练点1 等式的基本性质
1.将3x-7=2x变形正确的是( )
A.3x+2x=7 B.3x-2x= -7 C.3x+2x= -7 D.3x-2x=7
2.下列变形中,正确的是( )
A.由2+x=3得x=3+2 B.由2x=3x+4得2x-3x=4
C.由3x=2得 D.由x=0得3x=3
3.在物理学中,导体中的电流I跟导体两端的电压U、导体的电阻R之间有以下关系: 去分母得 IR=U,那么其变形的依据是___________.
4.已知m+a=n+b,根据等式的基本性质变形为m=n,那么a,b必须符合的条件是________.
练点2 等式的基本性质的应用
5.下列方程变形错误的是( )
A.由 得y=2 B.由-5x=2,得
C.由3+x=5,得x=2 D.由3=x-2,得x=5
6.已知2m-1=2n,利用等式的基本性质比较m与n的大小,则( )
无法比较
7.若a+2b+3c=10,且4a+3b+2c=15,则a+b+c=__________.
8.若m+3=1,则m的倒数是_________.
9.阅读框图,在四个步骤中,不是依据等式的基本性质变形的是_________(填序号).
纠易错 忽视除式不为0 而错用等式的基本性质
10.下列变形中,错误的是( )
A.若x=y,则xm-6=ym-6 B.若a=b,则
C.若x=3,则x =3x D.若mx=nx,则m=n
整合方法提升练
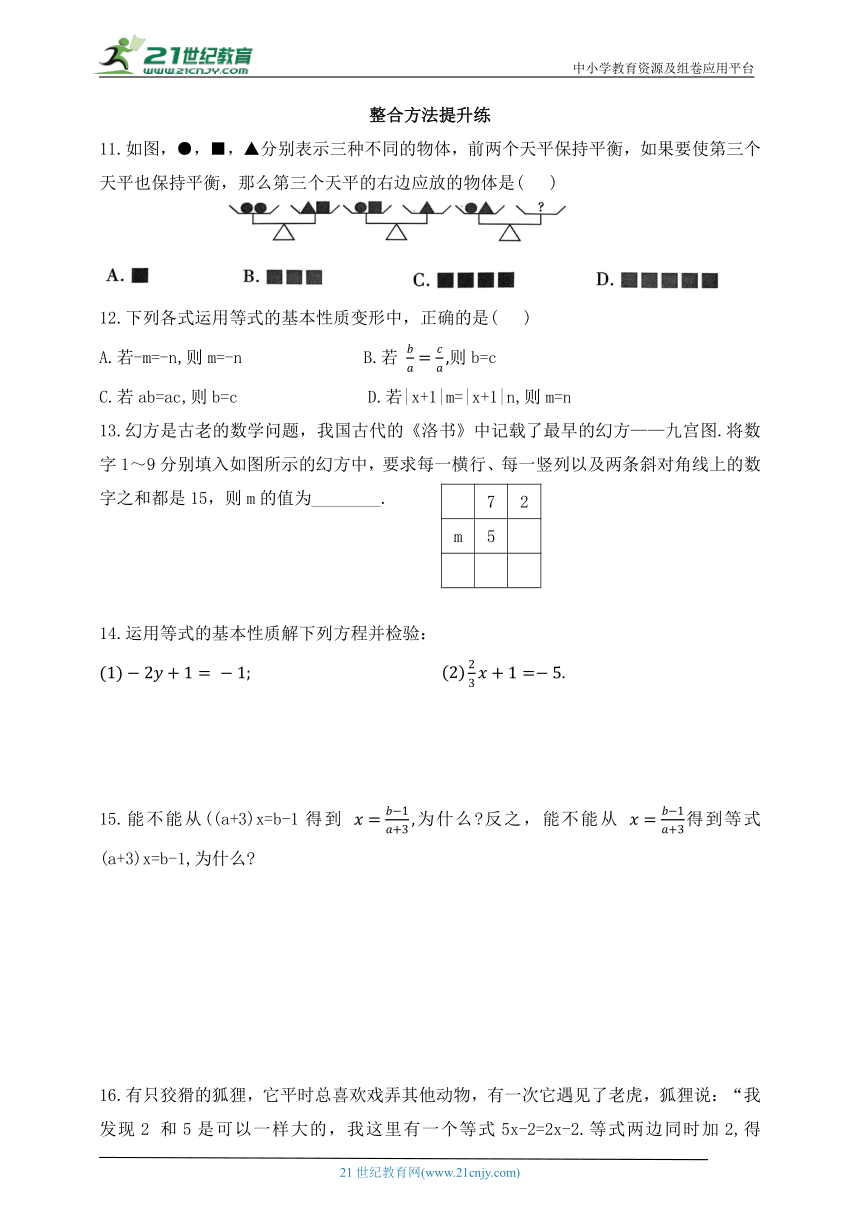
11.如图,●,■,▲分别表示三种不同的物体,前两个天平保持平衡,如果要使第三个天平也保持平衡,那么第三个天平的右边应放的物体是( )
12.下列各式运用等式的基本性质变形中,正确的是( )
A.若-m=-n,则m=-n B.若 则b=c
C.若ab=ac,则b=c D.若|x+1|m=|x+1|n,则m=n
7 2
m 5
13.幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫图.将数字1~9分别填入如图所示的幻方中,要求每一横行、每一竖列以及两条斜对角线上的数字之和都是15,则m的值为________.
14.运用等式的基本性质解下列方程并检验:
15.能不能从((a+3)x=b-1得到 为什么 反之,能不能从 得到等式(a+3)x=b-1,为什么
16.有只狡猾的狐狸,它平时总喜欢戏弄其他动物,有一次它遇见了老虎,狐狸说:“我发现2 和5是可以一样大的,我这里有一个等式5x-2=2x-2.等式两边同时加2,得5x-2+2=2x-2+2①,即5x=2x.等式两边同时除以x,得5=2②.”老虎瞪大了眼睛,听傻了.
你认为狐狸的说法正确吗 如果正确,请说明上述①②步的理由;如果不正确,请指出错在哪里,并加以改正.
探究培优拓展练
17.a,b,c三个物体的质量关系如图所示:
回答下列问题:
(1)a,b,c三个物体就单个而言,哪个质量最大
(2)若天平一边放一些物体a,另一边放一些物体c,要使天平平衡,天平两边至少应该分别放几个物体a和物体c
参考答案
1. D【点拨】等式两边都加7,得3x=2x+7,等式两边都减2x,得3x-2x=7.
2. B 【点拨】A.在等式2+x=3的两边同时减去2,可得x=3-2,原变形错误;B.在等式2x=3x+4的两边同时减去3x,可得2x-3x=4,原变形正确;C.在等式3x=2的两边同时除以3,可得 原变形错误;D.在等式x=0的两边同时乘3,可得3x=0,原变形错误.
3.等式的基本性质2 【点拨】将等式 去分母得IR=U,实质上是在等式的两边同时乘R,用到的是等式的基本性质2.
4. a=b 【点拨】由等式的基本性质1可知,等式两边同时减去一个相同的数,等式仍然成立,所以a=b.
5. B
6. A 【点拨】等式两边同时除以2,得 等式两边同时减去n,得
等式两边同时加上 得 所以m>n.
7.5 【点拨】因为a+2b+3c=10①,4a+3b+2c=15②,①+②得5a+5b+5c=25,所以a+b+c=5.
【点拨】方程两边同时减去3,得m+3-3=1-3,即m=-2,所以m的倒数为
9.③ 【点拨】①是等式两边都乘10,②是等式两边都减2x,③不是依据等式的基本性质变形的,④是等式两边都除以3.
10. D 【诊断】错解C 选项误以为没有应用等式的基本性质,而是左边平方,右边乘x,实际是两边同时乘x,因而C选项是正确的;A选项两边在同时乘m的基础上再同时减6,A正确;B选项两边同时除以t +1(t +1≠0),故B 正确. D选项两边同时除以x,其中x可能为0,故D错误.
11. D 【点拨】由题意知在第二个天平两边都加入一个■,对比第一个天平即可得出●=■■,把第二个天平中的●换成■■,则▲=■■■,所以●▲=■■■■■.
12. B 【点拨】A.由-m=-n,得m=n,原变形错误;B.由 得b=c,原变形正确;C.由ab=ac,得b=c,必须规定a≠0,原变形错误;D.由|x+1|m=|x+1|n,得 m=n,必须规定|x+1|≠0,原变形错误.故选B.
① 7 2
m 5
②
13.1 【点拨】如图,由题意可得①表示的数是15-7-2=6,②表示的数是15-2-5=8,则6+m+8=15,解得m=1.
14.【解】(1)两边同减1,得-2y= -2,两边同除以-2,得y=1.
检验:当y=1时,左边= -2y+1= -2+1= -1=右边,所以y=1是方程-2y+1= -1的解.
(2)两边同减1,得 两边同除以 得x=-9.
检验:当x=-9时,左边 1=-5=右边,
所以x= -9是方程 的解.
15.【解】不能从(a+3)x=b-1得到. 因为a+3可能为0,而0不能为除数.能从 得到等式(a+3)x=b-1,这是根据等式的基本性质2得到的,且由 可知,a+3≠0.
16.【解】狐狸的说法不正确.
错在第②步,当x=0时,等式两边不能同时除以x.
改正:由5x=2x,等式两边同减去2x,得3x=0.
等式两边同除以3,得x=0.
17.【解】(1)根据题图知2a=3b,2b=3c,则 进而有
因为 所以a>b>c,所以a,b,c三个物体就单个而言,a质量最大.
(2)由(1)知 即4a=9c,所以要使天平平衡,则天平两边至少应该分别放4个物体a和9个物体c.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四章 一元一次方程
1 等式与方程
第2课时 等式的基本性质
夯实基础逐点练习
练点1 等式的基本性质
1.将3x-7=2x变形正确的是( )
A.3x+2x=7 B.3x-2x= -7 C.3x+2x= -7 D.3x-2x=7
2.下列变形中,正确的是( )
A.由2+x=3得x=3+2 B.由2x=3x+4得2x-3x=4
C.由3x=2得 D.由x=0得3x=3
3.在物理学中,导体中的电流I跟导体两端的电压U、导体的电阻R之间有以下关系: 去分母得 IR=U,那么其变形的依据是___________.
4.已知m+a=n+b,根据等式的基本性质变形为m=n,那么a,b必须符合的条件是________.
练点2 等式的基本性质的应用
5.下列方程变形错误的是( )
A.由 得y=2 B.由-5x=2,得
C.由3+x=5,得x=2 D.由3=x-2,得x=5
6.已知2m-1=2n,利用等式的基本性质比较m与n的大小,则( )
无法比较
7.若a+2b+3c=10,且4a+3b+2c=15,则a+b+c=__________.
8.若m+3=1,则m的倒数是_________.
9.阅读框图,在四个步骤中,不是依据等式的基本性质变形的是_________(填序号).
纠易错 忽视除式不为0 而错用等式的基本性质
10.下列变形中,错误的是( )
A.若x=y,则xm-6=ym-6 B.若a=b,则
C.若x=3,则x =3x D.若mx=nx,则m=n
整合方法提升练
11.如图,●,■,▲分别表示三种不同的物体,前两个天平保持平衡,如果要使第三个天平也保持平衡,那么第三个天平的右边应放的物体是( )
12.下列各式运用等式的基本性质变形中,正确的是( )
A.若-m=-n,则m=-n B.若 则b=c
C.若ab=ac,则b=c D.若|x+1|m=|x+1|n,则m=n
7 2
m 5
13.幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫图.将数字1~9分别填入如图所示的幻方中,要求每一横行、每一竖列以及两条斜对角线上的数字之和都是15,则m的值为________.
14.运用等式的基本性质解下列方程并检验:
15.能不能从((a+3)x=b-1得到 为什么 反之,能不能从 得到等式(a+3)x=b-1,为什么
16.有只狡猾的狐狸,它平时总喜欢戏弄其他动物,有一次它遇见了老虎,狐狸说:“我发现2 和5是可以一样大的,我这里有一个等式5x-2=2x-2.等式两边同时加2,得5x-2+2=2x-2+2①,即5x=2x.等式两边同时除以x,得5=2②.”老虎瞪大了眼睛,听傻了.
你认为狐狸的说法正确吗 如果正确,请说明上述①②步的理由;如果不正确,请指出错在哪里,并加以改正.
探究培优拓展练
17.a,b,c三个物体的质量关系如图所示:
回答下列问题:
(1)a,b,c三个物体就单个而言,哪个质量最大
(2)若天平一边放一些物体a,另一边放一些物体c,要使天平平衡,天平两边至少应该分别放几个物体a和物体c
参考答案
1. D【点拨】等式两边都加7,得3x=2x+7,等式两边都减2x,得3x-2x=7.
2. B 【点拨】A.在等式2+x=3的两边同时减去2,可得x=3-2,原变形错误;B.在等式2x=3x+4的两边同时减去3x,可得2x-3x=4,原变形正确;C.在等式3x=2的两边同时除以3,可得 原变形错误;D.在等式x=0的两边同时乘3,可得3x=0,原变形错误.
3.等式的基本性质2 【点拨】将等式 去分母得IR=U,实质上是在等式的两边同时乘R,用到的是等式的基本性质2.
4. a=b 【点拨】由等式的基本性质1可知,等式两边同时减去一个相同的数,等式仍然成立,所以a=b.
5. B
6. A 【点拨】等式两边同时除以2,得 等式两边同时减去n,得
等式两边同时加上 得 所以m>n.
7.5 【点拨】因为a+2b+3c=10①,4a+3b+2c=15②,①+②得5a+5b+5c=25,所以a+b+c=5.
【点拨】方程两边同时减去3,得m+3-3=1-3,即m=-2,所以m的倒数为
9.③ 【点拨】①是等式两边都乘10,②是等式两边都减2x,③不是依据等式的基本性质变形的,④是等式两边都除以3.
10. D 【诊断】错解C 选项误以为没有应用等式的基本性质,而是左边平方,右边乘x,实际是两边同时乘x,因而C选项是正确的;A选项两边在同时乘m的基础上再同时减6,A正确;B选项两边同时除以t +1(t +1≠0),故B 正确. D选项两边同时除以x,其中x可能为0,故D错误.
11. D 【点拨】由题意知在第二个天平两边都加入一个■,对比第一个天平即可得出●=■■,把第二个天平中的●换成■■,则▲=■■■,所以●▲=■■■■■.
12. B 【点拨】A.由-m=-n,得m=n,原变形错误;B.由 得b=c,原变形正确;C.由ab=ac,得b=c,必须规定a≠0,原变形错误;D.由|x+1|m=|x+1|n,得 m=n,必须规定|x+1|≠0,原变形错误.故选B.
① 7 2
m 5
②
13.1 【点拨】如图,由题意可得①表示的数是15-7-2=6,②表示的数是15-2-5=8,则6+m+8=15,解得m=1.
14.【解】(1)两边同减1,得-2y= -2,两边同除以-2,得y=1.
检验:当y=1时,左边= -2y+1= -2+1= -1=右边,所以y=1是方程-2y+1= -1的解.
(2)两边同减1,得 两边同除以 得x=-9.
检验:当x=-9时,左边 1=-5=右边,
所以x= -9是方程 的解.
15.【解】不能从(a+3)x=b-1得到. 因为a+3可能为0,而0不能为除数.能从 得到等式(a+3)x=b-1,这是根据等式的基本性质2得到的,且由 可知,a+3≠0.
16.【解】狐狸的说法不正确.
错在第②步,当x=0时,等式两边不能同时除以x.
改正:由5x=2x,等式两边同减去2x,得3x=0.
等式两边同除以3,得x=0.
17.【解】(1)根据题图知2a=3b,2b=3c,则 进而有
因为 所以a>b>c,所以a,b,c三个物体就单个而言,a质量最大.
(2)由(1)知 即4a=9c,所以要使天平平衡,则天平两边至少应该分别放4个物体a和9个物体c.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
