5.5.1 两角和与差的正弦、余弦和正切公式(第3课时) 课件(共14张PPT)
文档属性
| 名称 | 5.5.1 两角和与差的正弦、余弦和正切公式(第3课时) 课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 615.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-11 14:30:09 | ||
图片预览






文档简介
(共14张PPT)
5.4.3
必修第一册
两角和与差的正弦、余弦
和正切公式(第3课时)
01
正弦的二倍角公式
探究:由S(α±β),C(α±β),T(α±β)是否能推导出sin2α, cos2α,tan2α的公式?
S(α±β)
令β=α
02
余弦的二倍角公式
探究:由S(α±β),C(α±β),T(α±β)是否能推导出sin2α, cos2α,tan2α的公式?
C(α±β)
令β=α
探究:由S(α±β),C(α±β),T(α±β)是否能推导出sin2α, cos2α,tan2α的公式?
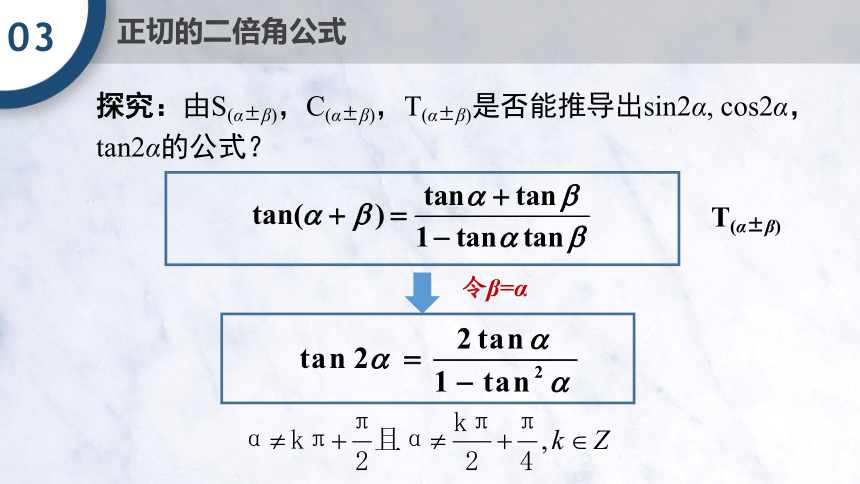
03
正切的二倍角公式
T(α±β)
令β=α
04
总结:二倍角公式
左到右:升幂缩角; 右到左:降幂扩角
应用公式求三角函数值
求cosα是否有其它方法?
例1 已知 ,求sin2α, cos2α,tan2α的值.
应用公式求三角函数值
例1 已知 ,求sin2α, cos2α,tan2α的值.
应用公式求三角函数值
变式:已知 ,求sin4α, cos4α,tan4α的值.
解:
应用公式求三角函数值
例2:在 ABC中, ,求tan(2A+2B)的值.
解法1:
cos A
sin A
tan A
tan 2A
判断角A的范围
正切的二倍角公式
tan 2B
tan B
tan (2A+2B)
正切的两角和公式
应用公式求三角函数值
例2:在 ABC中, ,求tan(2A+2B)的值.
解法2:
cos A
sin A
tan A
判断角A的范围
正切的二倍角公式
tan B
tan (A+B)
正切的两角和公式
tan2 (A+B)
应用公式求三角函数值
变式:已知 ,求sinα, cosα,tanα的值.
练习 1.
分析:对比公式
应用公式求三角函数值
练习 2. 化简
请用二倍角的正弦公式:
变式:化简
应用公式求三角函数值
练习 3. 化简
公式:利用
练习 4. 化简
练习5
应用公式求三角函数值
练习6
练习7
5.4.3
必修第一册
两角和与差的正弦、余弦
和正切公式(第3课时)
01
正弦的二倍角公式
探究:由S(α±β),C(α±β),T(α±β)是否能推导出sin2α, cos2α,tan2α的公式?
S(α±β)
令β=α
02
余弦的二倍角公式
探究:由S(α±β),C(α±β),T(α±β)是否能推导出sin2α, cos2α,tan2α的公式?
C(α±β)
令β=α
探究:由S(α±β),C(α±β),T(α±β)是否能推导出sin2α, cos2α,tan2α的公式?
03
正切的二倍角公式
T(α±β)
令β=α
04
总结:二倍角公式
左到右:升幂缩角; 右到左:降幂扩角
应用公式求三角函数值
求cosα是否有其它方法?
例1 已知 ,求sin2α, cos2α,tan2α的值.
应用公式求三角函数值
例1 已知 ,求sin2α, cos2α,tan2α的值.
应用公式求三角函数值
变式:已知 ,求sin4α, cos4α,tan4α的值.
解:
应用公式求三角函数值
例2:在 ABC中, ,求tan(2A+2B)的值.
解法1:
cos A
sin A
tan A
tan 2A
判断角A的范围
正切的二倍角公式
tan 2B
tan B
tan (2A+2B)
正切的两角和公式
应用公式求三角函数值
例2:在 ABC中, ,求tan(2A+2B)的值.
解法2:
cos A
sin A
tan A
判断角A的范围
正切的二倍角公式
tan B
tan (A+B)
正切的两角和公式
tan2 (A+B)
应用公式求三角函数值
变式:已知 ,求sinα, cosα,tanα的值.
练习 1.
分析:对比公式
应用公式求三角函数值
练习 2. 化简
请用二倍角的正弦公式:
变式:化简
应用公式求三角函数值
练习 3. 化简
公式:利用
练习 4. 化简
练习5
应用公式求三角函数值
练习6
练习7
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
