1.2 全等三角形 课件 (共21张PPT)2023—2024学年苏科版数学八年级上册
文档属性
| 名称 | 1.2 全等三角形 课件 (共21张PPT)2023—2024学年苏科版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 813.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-11 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
1.2 全等三角形
八年级(上册)
初中数学
这两个图形有怎样的关系?
1.2 全等三角形
情境创设
这两个图形有怎样的关系?
1.2 全等三角形
这两个图形有怎样的关系?
1.2 全等三角形
这两个图形有怎样的关系?
1.2 全等三角形
这两个图形有怎样的关系?
1.2 全等三角形
以上各组中的图形
都能完全重合,每一组图形都是全等形.
1.2 全等三角形
两个完全重合的三角形叫做全等三角形.
记作: △ABC≌△DEF.
自主反馈
C
A
B
F
D
E
1.2 全等三角形
C
A
B
F
D
E
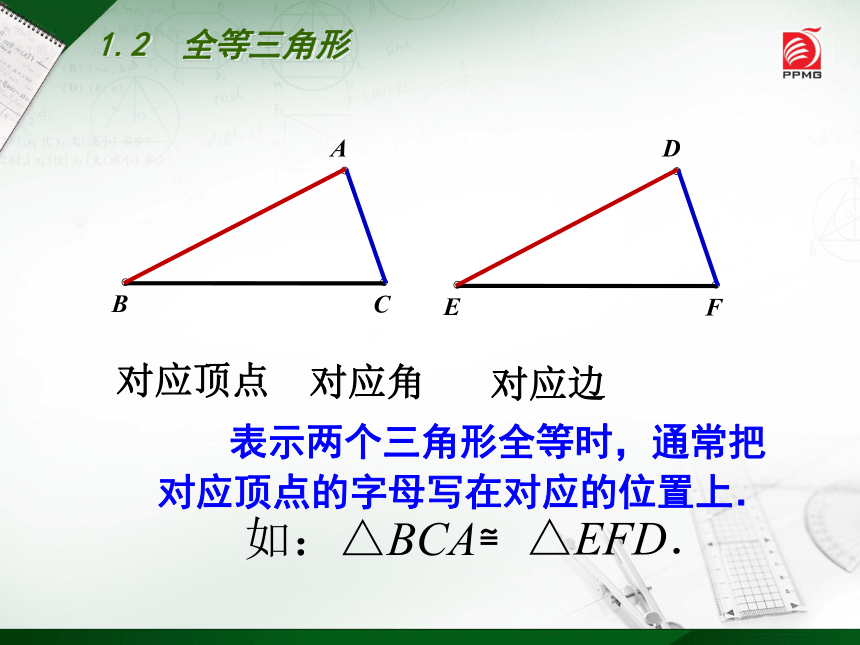
对应顶点
对应边
对应角
表示两个三角形全等时,通常把对应顶点的字母写在对应的位置上.
如:△BCA≌
△EFD.
1.2 全等三角形
∴ ∠A=∠D,∠B=∠E,∠C =∠F
(全等三角形的对应角相等).
∵△ABC ≌ △DEF (已知),
∴AB=DE,BC=EF,AC=DF
(全等三角形的对应边相等),
A
B
C
D
E
F
1.2 全等三角形
3.小组内讨论交流.
4.各组代表展示.
合作探究
要求:
1.任意剪两个全等的三角形.
2.利用这两个全等三角形组合新的图形.
1.2 全等三角形
思考:怎样改变△ABC的位置,使它与△DEF重合?
A
B
C
两个全等三角形的位置变化了,对应边、对应角的大小有变化吗?由此你能得到什么结论?
A
B
C
D
E
C
A
B
F
B
A
D
C
E
F
D
E
F
1.2 全等三角形
1.如图△ABD ≌ △CDB,
若AB=4,AD=5,BD=6, ∠ABD=30°,则BC=_____,CD=_____,∠CDB=_____.
A
B
D
C
尝试交流
1.2 全等三角形
A
O
D
C
B
2.如图△ABC ≌ △DCB,
(1)写出图中相等的边和角.
(2)若∠A=100°,∠DBC=20°,
求∠D和∠ABC的度数.
1.2 全等三角形
回顾反思
课堂小结
基础知识:
从观察全等图形着手,类比归纳出全等三角形的有关概念,会用几何语言表示两个三角形全等,会在全等三角形中正确地找出对应顶点、对应边、对应角.
用运动变化的观点让学生经历平移、翻折、旋转等全等变换的过程,了解用图形变换识别全等三角形的方法.
基本思想方法:
1.2 全等三角形
当堂检测
1.如图,△ABC≌△ADE,∠C=50°,∠D=45°,
∠CFA=75°,求∠BAC和∠BAE的度数.
A
B
C
D
E
F
1.2 全等三角形
2.如图,△ABC≌△DEF,B与E,C与F是对应顶点.通过怎样的图形变换可以使这两个三角形重合?
1.2 全等三角形
课堂总结反思
1.2 全等三角形
重合
顶点的字母
位置
对应边
对应角
课后作业
习题1.2第1、2、3题.
1.2 全等三角形
1.2 全等三角形
八年级(上册)
初中数学
这两个图形有怎样的关系?
1.2 全等三角形
情境创设
这两个图形有怎样的关系?
1.2 全等三角形
这两个图形有怎样的关系?
1.2 全等三角形
这两个图形有怎样的关系?
1.2 全等三角形
这两个图形有怎样的关系?
1.2 全等三角形
以上各组中的图形
都能完全重合,每一组图形都是全等形.
1.2 全等三角形
两个完全重合的三角形叫做全等三角形.
记作: △ABC≌△DEF.
自主反馈
C
A
B
F
D
E
1.2 全等三角形
C
A
B
F
D
E
对应顶点
对应边
对应角
表示两个三角形全等时,通常把对应顶点的字母写在对应的位置上.
如:△BCA≌
△EFD.
1.2 全等三角形
∴ ∠A=∠D,∠B=∠E,∠C =∠F
(全等三角形的对应角相等).
∵△ABC ≌ △DEF (已知),
∴AB=DE,BC=EF,AC=DF
(全等三角形的对应边相等),
A
B
C
D
E
F
1.2 全等三角形
3.小组内讨论交流.
4.各组代表展示.
合作探究
要求:
1.任意剪两个全等的三角形.
2.利用这两个全等三角形组合新的图形.
1.2 全等三角形
思考:怎样改变△ABC的位置,使它与△DEF重合?
A
B
C
两个全等三角形的位置变化了,对应边、对应角的大小有变化吗?由此你能得到什么结论?
A
B
C
D
E
C
A
B
F
B
A
D
C
E
F
D
E
F
1.2 全等三角形
1.如图△ABD ≌ △CDB,
若AB=4,AD=5,BD=6, ∠ABD=30°,则BC=_____,CD=_____,∠CDB=_____.
A
B
D
C
尝试交流
1.2 全等三角形
A
O
D
C
B
2.如图△ABC ≌ △DCB,
(1)写出图中相等的边和角.
(2)若∠A=100°,∠DBC=20°,
求∠D和∠ABC的度数.
1.2 全等三角形
回顾反思
课堂小结
基础知识:
从观察全等图形着手,类比归纳出全等三角形的有关概念,会用几何语言表示两个三角形全等,会在全等三角形中正确地找出对应顶点、对应边、对应角.
用运动变化的观点让学生经历平移、翻折、旋转等全等变换的过程,了解用图形变换识别全等三角形的方法.
基本思想方法:
1.2 全等三角形
当堂检测
1.如图,△ABC≌△ADE,∠C=50°,∠D=45°,
∠CFA=75°,求∠BAC和∠BAE的度数.
A
B
C
D
E
F
1.2 全等三角形
2.如图,△ABC≌△DEF,B与E,C与F是对应顶点.通过怎样的图形变换可以使这两个三角形重合?
1.2 全等三角形
课堂总结反思
1.2 全等三角形
重合
顶点的字母
位置
对应边
对应角
课后作业
习题1.2第1、2、3题.
1.2 全等三角形
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
