九年级数学上分层优化堂堂清(15)第二十二章 二次函数综合素质测评试题(含解析)
文档属性
| 名称 | 九年级数学上分层优化堂堂清(15)第二十二章 二次函数综合素质测评试题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-11 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
九年级数学上分层优化堂堂清
二十二章 二次函数
本章综合素质测评
时间90分钟满分120分
填空题(每小题3分,共30分)
1 .下列函数中,二次函数是( )
A. y=﹣4x+5 B. y=x(2x﹣3)
C. y=(x+4)2﹣x2 D. y=
二次函数y=3x2+2x的图象的对称轴为( )
A. x=﹣2 B. x=﹣3 C. x= D. x=
将抛物线y=x2+2x﹣3的图象先向左平移2个单位,再向上平移3个单位,得到的抛物线的解析式是( )
A. y=(x﹣1)2﹣1 B. y=(x+3)2﹣1
C. y=(x﹣1)2﹣7 D. y=(x+3)2﹣7
4 .对于抛物线y=﹣2(x+1)2+3,下列结论:
①抛物线的开口向下;
②对称轴为直线x=1:
③顶点坐标为(﹣1,3);
④x>1时,y随x的增大而减小.
其中正确结论的个数为( )
A. 1 B. 2 C. 3 D. 4
5 .已知二次函数y=x2-2mx+m2+1(m为常数),当自变量x的值满足-3≤x≤-1时,与其对应的函数值y的最小值为5,则m的值为( )
A. 1或-3 B. -3或-5 C. 1或-5 D. 1或-1
6 .根据表中的二次函数y=ax2+bx+c的自变量x与函数y的对应值,可判断该二次函数的图象与x轴( )
x … ﹣1 0 1 2 …
y … 4 ﹣0.5 ﹣2 ﹣0.5 …
A. 只有一个交点 B. 有两个交点,且它们分别在y轴两侧
C. 有两个交点,且它们均在y轴同侧 D. 无交点
7 .抛物线y=(x﹣1)2+t与x轴的两个交点之间的距离为4,则t的值是( )
A. ﹣1 B. ﹣2 C. ﹣3 D. ﹣4
8 .如图,在矩形ABCD中,AB=a,BC=b,≤a≤3b,AE=AH=CF=CG,则四边形EFGH的面积的最大值是( )
A. B. C. D.
9 .当a﹣1≤x≤a时,函数y=x2﹣2x+1的最小值为1,则a的值为( )
A. 1 B. 2 C. 1或2 D. 0或3
10 .已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有( )
A. 2个 B. 3个 C. 4个 D. 5个
填空题(每小题3分,共15分)
11 .把二次函数y=x2﹣2x+3的图象绕原点旋转180°后得到的图象的函数解析式为_____.
12 .由于被墨水污染,一道数学题仅能见到如下文字:已知二次函数y=ax2+bx+c的图象过点(1,0)……,求证:这个二次函数的图象关于直线x=2对称,根据现有信息,得出有关这个二次函数的下列结论:①过点(3,0);②顶点(2,2);③在x轴上截得的线段的长是2;④与y轴的交点是(0,3),其中正确的是______(填序号).
13 .飞机着陆后滑行的距离s(单位:m)与滑行的时间t(单位:s)的函数解析式是s=60t -1.2t 2,飞机着陆后滑行______秒才能停下来.
14 .函数y=ax2﹣2ax+m(a>0)的图象过点(2,0),那么使函数值y<0成立的x的取值范围是______.
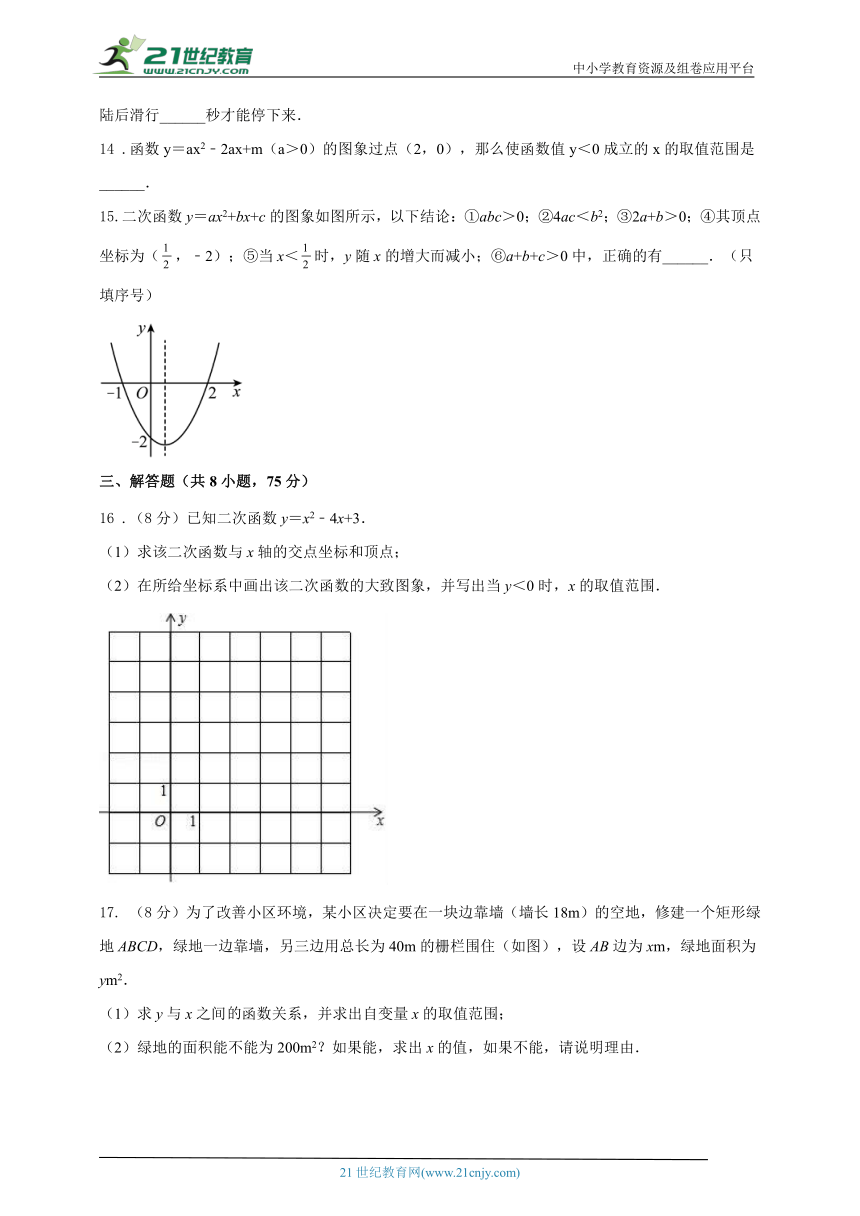
15.二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(,﹣2);⑤当x<时,y随x的增大而减小;⑥a+b+c>0中,正确的有______.(只填序号)
解答题(共8小题,75分)
16 .(8分)已知二次函数y=x2﹣4x+3.
(1)求该二次函数与x轴的交点坐标和顶点;
(2)在所给坐标系中画出该二次函数的大致图象,并写出当y<0时,x的取值范围.
(8分)为了改善小区环境,某小区决定要在一块边靠墙(墙长18m)的空地,修建一个矩形绿地ABCD,绿地一边靠墙,另三边用总长为40m的栅栏围住(如图),设AB边为xm,绿地面积为ym2.
(1)求y与x之间函数关系,并求出自变量x的取值范围;
(2)绿地的面积能不能为200m2?如果能,求出x的值,如果不能,请说明理由.
18 .(9分)某超市销售一种水果,进价为每箱40元,规定售价不低于进价.现在的售价为每箱72元,每月可销售60箱.经市场调查发现:若这种水果的售价每降低2元,则每月的销量将增加10箱,设每箱水果降价x元(x为偶数),每月的销量为y箱.
(1)写出y与x之间的函数关系式和自变量x的取值范围.
(2)若该超市在销售过程中每月需支出其他费用500元,则如何定价才能使每月销售水果的利润最大?最大利润是多少元?
19 .(8分)某电商在购物平台上销售一款小电器,其进价为45元/件,每销售一件需缴纳平台推广费5元,该款小电器每天的销售量y(件)与每件的销售价格x(元)满足函数关系:y=﹣2x+200.为保证市场稳定,供货商规定销售价格不得低于75元/件.
(1)写出每天的销售利润w(元)与销售价格x(元)的函数关系式(不必写出x的取值范围);
(2)每件小电器的销售价格定为多少元时,才能使该款小电器每天获得的利润是1200元?
20 .(8分)已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点为(0,3).
(1)求此二次函数的解析式;
(2)结合函数图象,直接写出当y≤﹣1时x的取值范围.
21 .(9分)请阅读下列材料,并完成相应的任务:
定义:我们把自变量为的二次函数与(,)称为一对“亲密函数”,如的“亲密函数”是.
任务:
(1)写出二次函数的“亲密函数”:______;
(2)二次函数的图像与轴交点的横坐标为1和,它的“亲密函数”的图像与轴交点的横坐标为______,猜想二次函数()的图像与轴交点的横坐标与其“亲密函数”的图像与轴交点的横坐标之间的关系是______;
(3)二次函数的图像与轴交点的横坐标为1和,请利用(2)中的结论直接写出二次函数的图像与轴交点的横坐标.
22 .(12分)已知抛物线的对称轴是直线,与轴相交于A,B两点(点B在点A右侧),与轴交于点C.
(1)求抛物线的解析式;
(2)如图,若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),是否存在点P,使四边形的面积最大?若存在,求点P的坐标及四边形面积的最大值;若不存在,请说明理由.
23.(13分)在平面直角坐标系中,抛物线经过点A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求该抛物线的函数表达式及顶点C的坐标;
(2)设该抛物线上一动点P的横坐标为t.
①在图1中,当﹣3<t<0时,求△PBO的面积S与t的函数关系式,并求S的最大值;
②在图2中,若点P在该抛物线上,点E在该抛物线的对称轴上,且以A,O,P,E为顶点的四边形是平行四边形,求点P的坐标;
九年级数学上分层优化堂堂清
二十二章 二次函数
本章综合素质测评(解析版)
时间90分钟满分120分
填空题(每小题3分,共30分)
1 .下列函数中,二次函数是( )
A. y=﹣4x+5 B. y=x(2x﹣3)
C. y=(x+4)2﹣x2 D. y=
【答案】B
【解析】
【分析】根据二次函数的定义逐项判断即可.
【详解】解:A. y=-4x+5是一次函数,不符合题意;
B. y= x(2x-3)=2x2-3x,是二次函数,符合题意;
C. y=(x+4)2 x2=8x+16,为一次函数,不符合题意;
D. y=是组合函数,不符合题意.
故选B.
【点评】本题考查二次函数的定义,熟知二次函数的表达形式是解答的关键.
二次函数y=3x2+2x的图象的对称轴为( )
A. x=﹣2 B. x=﹣3 C. x= D. x=
【答案】D
【解析】
【分析】利用对称轴公式求解即可
【详解】y=3x2+2x
x=-=-=
故选D
【点评】本题考查了二次函数的性质,熟练掌握对称轴公式是解题的关键.
将抛物线y=x2+2x﹣3的图象先向左平移2个单位,再向上平移3个单位,得到的抛物线的解析式是( )
A. y=(x﹣1)2﹣1 B. y=(x+3)2﹣1
C. y=(x﹣1)2﹣7 D. y=(x+3)2﹣7
【答案】B
【解析】
【分析】根据图象平移规律,可得答案.
【详解】函数化为一般式为,
的图象先向左平移2个单位,再向上平移3个单位,得
.
故选:.
【点评】本题考查了二次函数图象与几何变换,利用平移规律:左加右减,上加下减是解题关键.
4 .对于抛物线y=﹣2(x+1)2+3,下列结论:
①抛物线的开口向下;
②对称轴为直线x=1:
③顶点坐标为(﹣1,3);
④x>1时,y随x的增大而减小.
其中正确结论的个数为( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
【分析】根据二次函数的性质对各小题分析判断即可得解.
【详解】①∵a=-2,∴抛物线的开口向下,故本小题正确;
②对称轴为直线x=﹣1,故本小题错误;
③顶点坐标为(﹣1,3),故本小题正确;
④∵对称轴为直线x=﹣1,抛物线开口向下,∴x>﹣1时,y随x的增大而减小,∴x>1时,y随x的增大而减小,故本小题正确.
综上所述:正确的有①③④.
故选C.
【点评】本题考查了二次函数y=a(x﹣h)2+k的性质,主要是抛物线开口方向、对称轴、顶点坐标以及二次函数的增减性.
5 .已知二次函数y=x2-2mx+m2+1(m为常数),当自变量x的值满足-3≤x≤-1时,与其对应的函数值y的最小值为5,则m的值为( )
A. 1或-3 B. -3或-5 C. 1或-5 D. 1或-1
【答案】C
【解析】
【分析】利用配方法可得出:当x=m时,y的最小值为1.分m<-3,-3≤m≤-1和m>-1三种情况考虑:当m<-3时,由y的最小值为5可得出关于m的一元二次方程,解之取其较小值;当-3≤m≤-1时,y的最小值为1,舍去;当m>-1时,由y的最小值为5可得出关于m的一元二次方程,解之取其较大值.综上,此题得解.
【详解】∵y=x2-2mx+m2+1=(x-m)2+1,
∴当x=m时,y的最小值为1.
当m<-3时,在-3≤x≤-1中,y随x的增大而增大,
∴9+6m+m2+1=5,
解得:m1=-5,m2=-1(舍去);
当-3≤m≤-1时,y的最小值为1,舍去;
当m>-1时,在-3≤x≤-1中,y随x的增大而减小,
∴1+2m+m2+1=5,
解得:m1=-3(舍去),m2=1.
∴m的值为-5或1.
故选C.
【点评】本题考查了二次函数的最值以及二次函数图象上点的坐标特征,分m<-3,-3≤m≤-1和m>-1三种情况求出m的值是解题的关键.
6 .根据表中的二次函数y=ax2+bx+c的自变量x与函数y的对应值,可判断该二次函数的图象与x轴( )
x … ﹣1 0 1 2 …
y … 4 ﹣0.5 ﹣2 ﹣0.5 …
A. 只有一个交点 B. 有两个交点,且它们分别在y轴两侧
C. 有两个交点,且它们均在y轴同侧 D. 无交点
【答案】B
【解析】
【分析】由条件可求得抛物线解析式,再进行判断即可.
【详解】由题意可知抛物线过(0,﹣0.5),(1,﹣2),(﹣1,4),代入抛物线解析式可得:,解得:,
∴抛物线解析式为y=1.5x2﹣3x﹣0.5,
令y=0,可得:1.5x2﹣3x﹣0.5=0,
解得:x=1+>0或x=1﹣<0,
∴抛物线与x轴有两个交点,且它们都在y轴的两侧.
故选B.
【点评】本题主要考查二次函数的性质,利用待定系数法求得二次函数的解析式是解题的关键.
7 .抛物线y=(x﹣1)2+t与x轴的两个交点之间的距离为4,则t的值是( )
A. ﹣1 B. ﹣2 C. ﹣3 D. ﹣4
【答案】D
【解析】
【分析】先求出方程的两根,让两根之差的绝对值为4列式求值即可.
【详解】解:令y=0,则(x﹣1)2+t=0,
解得:x1=1﹣,x2=1+,
∵抛物线y=(x﹣1)2+t与x轴的两个交点之间的距离为4,
∴|x1﹣x2|=4,
∴(1+)﹣(1﹣)=4,
∴t=﹣4,
经检验t=﹣4是原方程的解.
故选D.
【点评】本题考查了抛物线与x轴的交点,二次函数与一元二次方程的关系,熟练掌握二次函数的图象和性质是解题的关键.
8 .如图,在矩形ABCD中,AB=a,BC=b,≤a≤3b,AE=AH=CF=CG,则四边形EFGH的面积的最大值是( )
A. B. C. D.
【答案】B
【解析】
【分析】先根据题意列出二次函数关系式,再根据求二次函数最值的方法求解即可.
【详解】设,则,,
设四边形的面积为,
依题意,得,
即:,
,抛物线开口向下,
时,有最大值,
,
,
函数有最大值为.
故选:.
【点评】根据面积的和差关系,建立函数关系式,此题为数学建模题,借助二次函数解决实际问题.
9 .当a﹣1≤x≤a时,函数y=x2﹣2x+1的最小值为1,则a的值为( )
A. 1 B. 2 C. 1或2 D. 0或3
【答案】D
【解析】
【分析】利用二次函数图象上点的坐标特征找出当时的值,结合当时函数有最小值1,即可得出关于的一元一次方程,解之即可得出结论.
【详解】当时,有,
解得:,,
当时,函数有最小值1,
或,
或.
故选:.
【点评】本题考查了二次函数图象上点的坐标特征以及二次函数的最值,利用二次函数图象上点的坐标特征找出当时的值是解题的关键.
10 .已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有( )
A. 2个 B. 3个 C. 4个 D. 5个
【答案】B
【解析】
【分析】由抛物线的图象可判断a、b、c的符号,可判断①;由x=-1和x=2时对应的函数值可判断②、③;由对称轴可得b=-2a分别代入a-b+c,借助函数图象可判断④;可以比较当x=m和x=1时的函数值的大小可判断⑤,可求得答案.
【详解】解:∵图象开口向下,与y轴的交点在x轴的上方,
∴a<0,c>0,
∵对称轴为x=1,
∴,
∴b=-2a>0,
∴abc<0,故①错误;
当x=-1时,可知y<0,
∴a-b+c<0,
∴a+c<b,故②错误;
∵抛物线与x的一个交点在-1和0之间,
∴另一个交点在2和3之间,
∴当x=2时,y>0,
∴4a+2b+c>0,故③正确;
∵b=-2a,
∴a=,且a-b+c<0,
∴,
即,
∴2c<3b,故④正确;
∵抛物线开口向下,
∴当x=1时,y有最大值,
∴a+b+c>am2+bm+c,
∴a+b>m(am+b),故⑤正确;
综上可知正确的有3个,
故选:B.
【点评】本题主要考查二次函数图象与系数的关系,掌握y=ax2+bx+c(a≠0)中各系数与其图象的关系是解题的关键.
填空题(每小题3分,共15分)
11 .把二次函数y=x2﹣2x+3的图象绕原点旋转180°后得到的图象的函数解析式为_____.
【答案】y=﹣x2﹣2x﹣3
【解析】
【分析】求出原抛物线的顶点坐标以及绕原点旋转180°后的抛物线的顶点坐标,再根据旋转后抛物线开口方向向下,利用顶点式解析式写出即可.
【详解】∵抛物线y=x2﹣2x+3=(x﹣1)2+1的顶点坐标为(1,1),
∴绕原点旋转180°后的抛物线的顶点坐标为(﹣1,﹣1),
∴所得到的图象的解析式为y=﹣(x+1)2﹣1,即y=﹣x2﹣2x﹣3.
故答案为y=﹣x2﹣2x﹣3.
【点评】本题考查了二次函数图象与几何变换,利用顶点的变化确定函数解析式的变化更简便.
12 .由于被墨水污染,一道数学题仅能见到如下文字:已知二次函数y=ax2+bx+c的图象过点(1,0)……,求证:这个二次函数的图象关于直线x=2对称,根据现有信息,得出有关这个二次函数的下列结论:①过点(3,0);②顶点(2,2);③在x轴上截得的线段的长是2;④与y轴的交点是(0,3),其中正确的是______(填序号).
【答案】①③
【解析】
【分析】利用抛物线的对称性得到抛物线与轴的另一个交点坐标为,从而得到抛物线在轴上截得的线段的长,利用和对称轴方程不能确定顶点的纵坐标和的值.
【详解】二次函数的图象过点,对称轴为直线,
抛物线与轴的另一个交点坐标为,
抛物线在轴上截得的线段的长是.
故答案为:①③.
【点评】本题考查了抛物线与轴的交点:把求二次函数(,,是常数,)与轴的交点坐标问题转化解.关于的一元二次方程即可求得交点横坐标.
13 .飞机着陆后滑行的距离s(单位:m)关于滑行的时间t(单位:s)的函数解析式是s=60t -1.2t 2,飞机着陆后滑行______秒才能停下来.
【答案】25
【解析】
【分析】将函数解析式配方成顶点式求出s取得最大值时的t的值即可得.
【详解】解:∵s=60t-1.2t2=-1.2(t-25)2+750,
∴当t=25时,s取得最大值750,
即飞机着陆后滑行25秒才能停下来,
故答案为:25.
【点评】本题主要考查二次函数的应用,理解题意得出飞机滑行的距离即为s的最大值是解题的关键.
14 .函数y=ax2﹣2ax+m(a>0)的图象过点(2,0),那么使函数值y<0成立的x的取值范围是______.
【答案】
【解析】
【分析】先求出抛物线的对称轴,由抛物线与x轴的交点(2,0)和对称轴就可以求出抛物线与x轴的另一个交点坐标,又因为抛物线开口向上,所以在x轴下方部分,,由抛物线与x轴两交点的横坐标,就可以求解.
【详解】解:∵函数
函数图像开口向上,对称轴x= -=1.
∵图像经过点(2,0),2-1=1,1-1=0
∴抛物线与x轴的另一个交点为即(0,0),在x轴下方部分,,
故当 时,.
【点评】本题考查抛物线的对称性,解答关键是由对称轴、抛物线与求出x轴的交点(2,0),求出抛物线与x轴的另一个交点坐标.
15.二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(,﹣2);⑤当x<时,y随x的增大而减小;⑥a+b+c>0中,正确的有______.(只填序号)
【答案】①②③⑤
【解析】
【分析】根据图象可判断①②③④⑤,由x=1时,y<0,可判断⑥.
【详解】由图象可得,a>0,c<0,b<0,△=b2﹣4ac>0,对称轴为x=,
∴abc>0,4ac<b2,当时,y随x的增大而减小.故①②⑤正确,
∵,
∴2a+b>0,
故③正确,
由图象可得顶点纵坐标小于﹣2,则④错误,
当x=1时,y=a+b+c<0,故⑥错误.
故答案为:①②③⑤.
【点评】本题考查的是二次函数图象与系数的关系,二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.
解答题(共8小题,75分)
16 .(8分)已知二次函数y=x2﹣4x+3.
(1)求该二次函数与x轴的交点坐标和顶点;
(2)在所给坐标系中画出该二次函数的大致图象,并写出当y<0时,x的取值范围.
【答案】(1)二次函数与x轴的交点坐标为(1,0)(3,0),抛物线的顶点坐标为(2,﹣1);
(2)图见详解;当y<0时,1<x<3.
【解析】
【分析】(1)令y=0,可求出x的值,即为与x轴的交点坐标;将二次函数化为顶点式即可得出顶点坐标
(2)根据与x轴的交点坐标,顶点坐标,与y轴的交点即可画出图像,再根据图像信息即可得出x的取值范围.
【详解】(1)当y=0时,x2﹣4x+3=0,解得x1=1,x2=3,
所以该二次函数与x轴的交点坐标为(1,0)(3,0);
因为y=x2﹣4x+3=x2﹣4x+4﹣1=(x﹣2)2﹣1,
所以抛物线顶点坐标为(2,﹣1);
(2)函数图象如图:
由图象可知,当y<0时,1<x<3.
【点评】本题考查了二次函数的图像及性质,熟练掌握二次函数的顶点式是解题的关键.
(8分)为了改善小区环境,某小区决定要在一块边靠墙(墙长18m)的空地,修建一个矩形绿地ABCD,绿地一边靠墙,另三边用总长为40m的栅栏围住(如图),设AB边为xm,绿地面积为ym2.
(1)求y与x之间函数关系,并求出自变量x的取值范围;
(2)绿地的面积能不能为200m2?如果能,求出x的值,如果不能,请说明理由.
【答案】(1)y与x之间的函数关系式是y=﹣2x2+40x(0<x<20);(2)绿化带的面积不能为200m2,理由见解析.
【解析】
【分析】(1)根据题意可以列出y与x之间的函数关系式并写出x的取值范围;
(2)先判断绿化带的面积能不能为200m2,然后说明理由即可解答本题.
【详解】(1) 由题意可得:y=x (40﹣2x)=﹣2x2+40x,
即y与x之间的函数关系式是y=﹣2x2+40x(0<x<20);
(2)绿化带的面积不能为200m2.理由如下:
将y=200代入y=﹣2x2+40x得:
200=﹣2x2+40x,
解得:x=10,
∴BC=40﹣2x=20>18,
∴绿化带面积不能为200m2.
【点评】本题考查了二次函数的应用、一元二次方程的应用,解答本题的关键是根据题意,列出相应的函数关系式和一元二次方程.
18 .(9分)某超市销售一种水果,进价为每箱40元,规定售价不低于进价.现在的售价为每箱72元,每月可销售60箱.经市场调查发现:若这种水果的售价每降低2元,则每月的销量将增加10箱,设每箱水果降价x元(x为偶数),每月的销量为y箱.
(1)写出y与x之间的函数关系式和自变量x的取值范围.
(2)若该超市在销售过程中每月需支出其他费用500元,则如何定价才能使每月销售水果的利润最大?最大利润是多少元?
【答案】(1)y=60+5x,(0≤x≤32,且x为偶数);(2)售价为62元时,每月销售水果的利润最大,最大利润是1920元.
【解析】
【分析】(1)根据价格每降低2元,平均每月多销售10箱,由每箱降价元,多卖,据此可以列出函数关系式;
(2)由利润=(售价 成本)×销售量 每月其他支出列出函数关系式,求出最大值.
【详解】解:(1)根据题意知y=60+5x,(0≤x≤32,且x为偶数);
(2)设每月销售水果的利润为w,
则w=(72﹣x﹣40)(5x+60)﹣500
=﹣5x2+100x+1420
=﹣5(x﹣10)2+1920,
当x=10时,w取得最大值,最大值为1920元,
答:当售价为62元时,每月销售水果的利润最大,最大利润是1920元.
【点评】本题主要考查二次函数的应用,由利润=(售价 成本)×销售量列出函数关系式求最值,用二次函数解决实际问题是解题的关键.
19 .(8分)某电商在购物平台上销售一款小电器,其进价为45元/件,每销售一件需缴纳平台推广费5元,该款小电器每天的销售量y(件)与每件的销售价格x(元)满足函数关系:y=﹣2x+200.为保证市场稳定,供货商规定销售价格不得低于75元/件.
(1)写出每天的销售利润w(元)与销售价格x(元)的函数关系式(不必写出x的取值范围);
(2)每件小电器的销售价格定为多少元时,才能使该款小电器每天获得的利润是1200元?
【答案】(1)w=﹣2x2+300x﹣10000;(2)每件小电器的销售价格定为80元时,才能使该款小电器每天获得的利润是1200元.
【解析】
【分析】(1)直接利用销量×每件的利润=总利润进而得出函数关系式;
(2)利用总利润=1200,进而解方程得出答案.
【详解】(1)由题意可得:w=(x﹣50)(﹣2x+200)=﹣2x2+300x﹣10000;
(2)由题意可得:1200=﹣2x2+300x﹣10000,
解得:x1=70(不合题意舍去),
x2=80,
答:每件小电器的销售价格定为80元时,才能使该款小电器每天获得的利润是1200元.
【点评】此题主要考查了一元二次方程的应用以及二次函数的应用,正确得出函数关系式是解题关键.
20 .(8分)已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点为(0,3).
(1)求此二次函数的解析式;
(2)结合函数图象,直接写出当y≤﹣1时x的取值范围.
【答案】(1)y=﹣x2+2x+3(2)当x≤1﹣或x≥1+时,y≤﹣1
【解析】
【分析】(1)利用待定系数法求抛物线解析式;
(2)先计算出y=-1对应的自变量的值,然后结合图象,写出y≤﹣1所对应的自变量的范围即可.
【详解】(1)把(-1,0)和(0,3)代入y=﹣x2+bx+c得:,解得:,所以抛物线解析式为y=﹣x2+2x+3;
(2)当y=-1时,﹣x2+2x+3=-1,解得:x1=1,x2=1,当x≤1或x≥1时,y≤﹣1.
【点评】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化解关于x的一元二次方程即可求得交点横坐标.也考查了二次函数的性质.
21 .(9分)请阅读下列材料,并完成相应的任务:
定义:我们把自变量为的二次函数与(,)称为一对“亲密函数”,如的“亲密函数”是.
任务:
(1)写出二次函数的“亲密函数”:______;
(2)二次函数的图像与轴交点的横坐标为1和,它的“亲密函数”的图像与轴交点的横坐标为______,猜想二次函数()的图像与轴交点的横坐标与其“亲密函数”的图像与轴交点的横坐标之间的关系是______;
(3)二次函数的图像与轴交点的横坐标为1和,请利用(2)中的结论直接写出二次函数的图像与轴交点的横坐标.
【答案】(1);(2)4和-1;互为相反数;(3)二次函数的图像与轴交点的横坐标为和
【分析】(1)根据二次函数的“亲密函数”定义把一次项系数变为相反数即可;
(2)利用“亲密函数”建立y=0时方程,解方程,得出“亲密函数”与x轴交点横坐标,与原函数与x轴交点横坐标比较,得出规律即可;
(3)先将函数变形,发现与“亲密函数”类似,根据原函数与x轴交点横坐标得出“亲密函数”与x轴交点横坐标,利用2x等于交点横坐标,求出x得出所求函数与x轴的交点横坐标即可.
【详解】解:(1)二次函数的“亲密函数”为,
故答案为:;
(2),解得,
它的“亲密函数”的图像与轴交点的横坐标为4和-1,
∴二次函数()的图像与轴交点的横坐标与其“亲密函数”的图像与轴交点的横坐标之间的关系是互为相反数;
故答案为4和-1;互为相反数;
(3),
∵二次函数的图像与轴交点的横坐标为1和,
∴二次函数的图像与轴交点的横坐标为-1和,
∴图像与轴交点的横坐标为-1和,
∴2x=-1,2x=2021,
∴,,
∴二次函数的图像与轴交点的横坐标为和.
【点评】本题考查新定义函数,仔细阅读题目,抓住实质,抛物线与x轴交点横坐标和一元二次方程的根,利用“亲密函数”变形得出新函数图像与x轴的交点横坐标是解题关键.
22 .(12分)已知抛物线的对称轴是直线,与轴相交于A,B两点(点B在点A右侧),与轴交于点C.
(1)求抛物线的解析式;
(2)如图,若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),是否存在点P,使四边形的面积最大?若存在,求点P的坐标及四边形面积的最大值;若不存在,请说明理由.
【思路点拨】
(1)根据对称轴公式,求出的值即可;
(2)连接,过点作轴交于点,设,再表示出,表示出的长,根据表示出,再根据二次函数求出最大值及的坐标,再根据即可.
【解题过程】
(1)解:抛物线的对称轴是直线,
,解得,
故抛物线的解析式为.
(2)解:连接,过点作轴交于点,设,
时,,
解得:,,,
,
设直线的解析式为,代入,,
得,解得:,
∴直线的解析式为,
,
∴,
,
当时,有最大值,最大值为,此时,
又,
故存在点,使四边形的面积最大,最大值为.
23.(13分)在平面直角坐标系中,抛物线经过点A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求该抛物线的函数表达式及顶点C的坐标;
(2)设该抛物线上一动点P的横坐标为t.
①在图1中,当﹣3<t<0时,求△PBO的面积S与t的函数关系式,并求S的最大值;
②在图2中,若点P在该抛物线上,点E在该抛物线的对称轴上,且以A,O,P,E为顶点的四边形是平行四边形,求点P的坐标;
【分析】(1)由待定系数法求函数的解析式即可;
(2)①求出直线BO的解析式,过点P作PG⊥x轴交BO于点G,可得E(t,﹣t)再由S(t)2,即可求解;
②设E(﹣1,m),根据平行四边形对角线的情况,分三种情况讨论:当AO为平行四边形的对角线时,当AP为平行四边形的对角线时,当AE为平行四边形的对角线时;利用中点坐标公式求解即可;
【解答】解:(1)设抛物线的解析式为y=ax2+bx,
将A(﹣2,0),B(﹣3,3)代入,
∴,
解得,
∴y=x2+2x,
∴C(﹣1,﹣1);
(2)①∵P的横坐标为t,
∴P(t,t2+2t),
设直线BO的解析式为y=kx,
∴﹣3k=3,
∴k=﹣1,
∴y=﹣x,
过点P作PG⊥x轴交BO于点G,
∴E(t,﹣t)
∴PG=﹣t﹣t2﹣2t=﹣t2﹣3t,
∴S3×(﹣t2﹣3t)(t)2,
∵﹣3<t<0,
∴t时,S有最大值;
②∵y=x2+2x,
∴抛物线的对称轴为直线x=﹣1,
设E(﹣1,m),
当AO为平行四边形的对角线时,
,
解得,
∴P(﹣1,﹣1);
当AP为平行四边形的对角线时,
,
解得,
∴P(1,3);
当AE为平行四边形的对角线时,
,
解得,
∴P(﹣3,3);
综上所述:P点坐标为(﹣1,﹣1)或(1,3)或(﹣3,3);
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学上分层优化堂堂清
二十二章 二次函数
本章综合素质测评
时间90分钟满分120分
填空题(每小题3分,共30分)
1 .下列函数中,二次函数是( )
A. y=﹣4x+5 B. y=x(2x﹣3)
C. y=(x+4)2﹣x2 D. y=
二次函数y=3x2+2x的图象的对称轴为( )
A. x=﹣2 B. x=﹣3 C. x= D. x=
将抛物线y=x2+2x﹣3的图象先向左平移2个单位,再向上平移3个单位,得到的抛物线的解析式是( )
A. y=(x﹣1)2﹣1 B. y=(x+3)2﹣1
C. y=(x﹣1)2﹣7 D. y=(x+3)2﹣7
4 .对于抛物线y=﹣2(x+1)2+3,下列结论:
①抛物线的开口向下;
②对称轴为直线x=1:
③顶点坐标为(﹣1,3);
④x>1时,y随x的增大而减小.
其中正确结论的个数为( )
A. 1 B. 2 C. 3 D. 4
5 .已知二次函数y=x2-2mx+m2+1(m为常数),当自变量x的值满足-3≤x≤-1时,与其对应的函数值y的最小值为5,则m的值为( )
A. 1或-3 B. -3或-5 C. 1或-5 D. 1或-1
6 .根据表中的二次函数y=ax2+bx+c的自变量x与函数y的对应值,可判断该二次函数的图象与x轴( )
x … ﹣1 0 1 2 …
y … 4 ﹣0.5 ﹣2 ﹣0.5 …
A. 只有一个交点 B. 有两个交点,且它们分别在y轴两侧
C. 有两个交点,且它们均在y轴同侧 D. 无交点
7 .抛物线y=(x﹣1)2+t与x轴的两个交点之间的距离为4,则t的值是( )
A. ﹣1 B. ﹣2 C. ﹣3 D. ﹣4
8 .如图,在矩形ABCD中,AB=a,BC=b,≤a≤3b,AE=AH=CF=CG,则四边形EFGH的面积的最大值是( )
A. B. C. D.
9 .当a﹣1≤x≤a时,函数y=x2﹣2x+1的最小值为1,则a的值为( )
A. 1 B. 2 C. 1或2 D. 0或3
10 .已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有( )
A. 2个 B. 3个 C. 4个 D. 5个
填空题(每小题3分,共15分)
11 .把二次函数y=x2﹣2x+3的图象绕原点旋转180°后得到的图象的函数解析式为_____.
12 .由于被墨水污染,一道数学题仅能见到如下文字:已知二次函数y=ax2+bx+c的图象过点(1,0)……,求证:这个二次函数的图象关于直线x=2对称,根据现有信息,得出有关这个二次函数的下列结论:①过点(3,0);②顶点(2,2);③在x轴上截得的线段的长是2;④与y轴的交点是(0,3),其中正确的是______(填序号).
13 .飞机着陆后滑行的距离s(单位:m)与滑行的时间t(单位:s)的函数解析式是s=60t -1.2t 2,飞机着陆后滑行______秒才能停下来.
14 .函数y=ax2﹣2ax+m(a>0)的图象过点(2,0),那么使函数值y<0成立的x的取值范围是______.
15.二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(,﹣2);⑤当x<时,y随x的增大而减小;⑥a+b+c>0中,正确的有______.(只填序号)
解答题(共8小题,75分)
16 .(8分)已知二次函数y=x2﹣4x+3.
(1)求该二次函数与x轴的交点坐标和顶点;
(2)在所给坐标系中画出该二次函数的大致图象,并写出当y<0时,x的取值范围.
(8分)为了改善小区环境,某小区决定要在一块边靠墙(墙长18m)的空地,修建一个矩形绿地ABCD,绿地一边靠墙,另三边用总长为40m的栅栏围住(如图),设AB边为xm,绿地面积为ym2.
(1)求y与x之间函数关系,并求出自变量x的取值范围;
(2)绿地的面积能不能为200m2?如果能,求出x的值,如果不能,请说明理由.
18 .(9分)某超市销售一种水果,进价为每箱40元,规定售价不低于进价.现在的售价为每箱72元,每月可销售60箱.经市场调查发现:若这种水果的售价每降低2元,则每月的销量将增加10箱,设每箱水果降价x元(x为偶数),每月的销量为y箱.
(1)写出y与x之间的函数关系式和自变量x的取值范围.
(2)若该超市在销售过程中每月需支出其他费用500元,则如何定价才能使每月销售水果的利润最大?最大利润是多少元?
19 .(8分)某电商在购物平台上销售一款小电器,其进价为45元/件,每销售一件需缴纳平台推广费5元,该款小电器每天的销售量y(件)与每件的销售价格x(元)满足函数关系:y=﹣2x+200.为保证市场稳定,供货商规定销售价格不得低于75元/件.
(1)写出每天的销售利润w(元)与销售价格x(元)的函数关系式(不必写出x的取值范围);
(2)每件小电器的销售价格定为多少元时,才能使该款小电器每天获得的利润是1200元?
20 .(8分)已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点为(0,3).
(1)求此二次函数的解析式;
(2)结合函数图象,直接写出当y≤﹣1时x的取值范围.
21 .(9分)请阅读下列材料,并完成相应的任务:
定义:我们把自变量为的二次函数与(,)称为一对“亲密函数”,如的“亲密函数”是.
任务:
(1)写出二次函数的“亲密函数”:______;
(2)二次函数的图像与轴交点的横坐标为1和,它的“亲密函数”的图像与轴交点的横坐标为______,猜想二次函数()的图像与轴交点的横坐标与其“亲密函数”的图像与轴交点的横坐标之间的关系是______;
(3)二次函数的图像与轴交点的横坐标为1和,请利用(2)中的结论直接写出二次函数的图像与轴交点的横坐标.
22 .(12分)已知抛物线的对称轴是直线,与轴相交于A,B两点(点B在点A右侧),与轴交于点C.
(1)求抛物线的解析式;
(2)如图,若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),是否存在点P,使四边形的面积最大?若存在,求点P的坐标及四边形面积的最大值;若不存在,请说明理由.
23.(13分)在平面直角坐标系中,抛物线经过点A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求该抛物线的函数表达式及顶点C的坐标;
(2)设该抛物线上一动点P的横坐标为t.
①在图1中,当﹣3<t<0时,求△PBO的面积S与t的函数关系式,并求S的最大值;
②在图2中,若点P在该抛物线上,点E在该抛物线的对称轴上,且以A,O,P,E为顶点的四边形是平行四边形,求点P的坐标;
九年级数学上分层优化堂堂清
二十二章 二次函数
本章综合素质测评(解析版)
时间90分钟满分120分
填空题(每小题3分,共30分)
1 .下列函数中,二次函数是( )
A. y=﹣4x+5 B. y=x(2x﹣3)
C. y=(x+4)2﹣x2 D. y=
【答案】B
【解析】
【分析】根据二次函数的定义逐项判断即可.
【详解】解:A. y=-4x+5是一次函数,不符合题意;
B. y= x(2x-3)=2x2-3x,是二次函数,符合题意;
C. y=(x+4)2 x2=8x+16,为一次函数,不符合题意;
D. y=是组合函数,不符合题意.
故选B.
【点评】本题考查二次函数的定义,熟知二次函数的表达形式是解答的关键.
二次函数y=3x2+2x的图象的对称轴为( )
A. x=﹣2 B. x=﹣3 C. x= D. x=
【答案】D
【解析】
【分析】利用对称轴公式求解即可
【详解】y=3x2+2x
x=-=-=
故选D
【点评】本题考查了二次函数的性质,熟练掌握对称轴公式是解题的关键.
将抛物线y=x2+2x﹣3的图象先向左平移2个单位,再向上平移3个单位,得到的抛物线的解析式是( )
A. y=(x﹣1)2﹣1 B. y=(x+3)2﹣1
C. y=(x﹣1)2﹣7 D. y=(x+3)2﹣7
【答案】B
【解析】
【分析】根据图象平移规律,可得答案.
【详解】函数化为一般式为,
的图象先向左平移2个单位,再向上平移3个单位,得
.
故选:.
【点评】本题考查了二次函数图象与几何变换,利用平移规律:左加右减,上加下减是解题关键.
4 .对于抛物线y=﹣2(x+1)2+3,下列结论:
①抛物线的开口向下;
②对称轴为直线x=1:
③顶点坐标为(﹣1,3);
④x>1时,y随x的增大而减小.
其中正确结论的个数为( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
【分析】根据二次函数的性质对各小题分析判断即可得解.
【详解】①∵a=-2,∴抛物线的开口向下,故本小题正确;
②对称轴为直线x=﹣1,故本小题错误;
③顶点坐标为(﹣1,3),故本小题正确;
④∵对称轴为直线x=﹣1,抛物线开口向下,∴x>﹣1时,y随x的增大而减小,∴x>1时,y随x的增大而减小,故本小题正确.
综上所述:正确的有①③④.
故选C.
【点评】本题考查了二次函数y=a(x﹣h)2+k的性质,主要是抛物线开口方向、对称轴、顶点坐标以及二次函数的增减性.
5 .已知二次函数y=x2-2mx+m2+1(m为常数),当自变量x的值满足-3≤x≤-1时,与其对应的函数值y的最小值为5,则m的值为( )
A. 1或-3 B. -3或-5 C. 1或-5 D. 1或-1
【答案】C
【解析】
【分析】利用配方法可得出:当x=m时,y的最小值为1.分m<-3,-3≤m≤-1和m>-1三种情况考虑:当m<-3时,由y的最小值为5可得出关于m的一元二次方程,解之取其较小值;当-3≤m≤-1时,y的最小值为1,舍去;当m>-1时,由y的最小值为5可得出关于m的一元二次方程,解之取其较大值.综上,此题得解.
【详解】∵y=x2-2mx+m2+1=(x-m)2+1,
∴当x=m时,y的最小值为1.
当m<-3时,在-3≤x≤-1中,y随x的增大而增大,
∴9+6m+m2+1=5,
解得:m1=-5,m2=-1(舍去);
当-3≤m≤-1时,y的最小值为1,舍去;
当m>-1时,在-3≤x≤-1中,y随x的增大而减小,
∴1+2m+m2+1=5,
解得:m1=-3(舍去),m2=1.
∴m的值为-5或1.
故选C.
【点评】本题考查了二次函数的最值以及二次函数图象上点的坐标特征,分m<-3,-3≤m≤-1和m>-1三种情况求出m的值是解题的关键.
6 .根据表中的二次函数y=ax2+bx+c的自变量x与函数y的对应值,可判断该二次函数的图象与x轴( )
x … ﹣1 0 1 2 …
y … 4 ﹣0.5 ﹣2 ﹣0.5 …
A. 只有一个交点 B. 有两个交点,且它们分别在y轴两侧
C. 有两个交点,且它们均在y轴同侧 D. 无交点
【答案】B
【解析】
【分析】由条件可求得抛物线解析式,再进行判断即可.
【详解】由题意可知抛物线过(0,﹣0.5),(1,﹣2),(﹣1,4),代入抛物线解析式可得:,解得:,
∴抛物线解析式为y=1.5x2﹣3x﹣0.5,
令y=0,可得:1.5x2﹣3x﹣0.5=0,
解得:x=1+>0或x=1﹣<0,
∴抛物线与x轴有两个交点,且它们都在y轴的两侧.
故选B.
【点评】本题主要考查二次函数的性质,利用待定系数法求得二次函数的解析式是解题的关键.
7 .抛物线y=(x﹣1)2+t与x轴的两个交点之间的距离为4,则t的值是( )
A. ﹣1 B. ﹣2 C. ﹣3 D. ﹣4
【答案】D
【解析】
【分析】先求出方程的两根,让两根之差的绝对值为4列式求值即可.
【详解】解:令y=0,则(x﹣1)2+t=0,
解得:x1=1﹣,x2=1+,
∵抛物线y=(x﹣1)2+t与x轴的两个交点之间的距离为4,
∴|x1﹣x2|=4,
∴(1+)﹣(1﹣)=4,
∴t=﹣4,
经检验t=﹣4是原方程的解.
故选D.
【点评】本题考查了抛物线与x轴的交点,二次函数与一元二次方程的关系,熟练掌握二次函数的图象和性质是解题的关键.
8 .如图,在矩形ABCD中,AB=a,BC=b,≤a≤3b,AE=AH=CF=CG,则四边形EFGH的面积的最大值是( )
A. B. C. D.
【答案】B
【解析】
【分析】先根据题意列出二次函数关系式,再根据求二次函数最值的方法求解即可.
【详解】设,则,,
设四边形的面积为,
依题意,得,
即:,
,抛物线开口向下,
时,有最大值,
,
,
函数有最大值为.
故选:.
【点评】根据面积的和差关系,建立函数关系式,此题为数学建模题,借助二次函数解决实际问题.
9 .当a﹣1≤x≤a时,函数y=x2﹣2x+1的最小值为1,则a的值为( )
A. 1 B. 2 C. 1或2 D. 0或3
【答案】D
【解析】
【分析】利用二次函数图象上点的坐标特征找出当时的值,结合当时函数有最小值1,即可得出关于的一元一次方程,解之即可得出结论.
【详解】当时,有,
解得:,,
当时,函数有最小值1,
或,
或.
故选:.
【点评】本题考查了二次函数图象上点的坐标特征以及二次函数的最值,利用二次函数图象上点的坐标特征找出当时的值是解题的关键.
10 .已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有( )
A. 2个 B. 3个 C. 4个 D. 5个
【答案】B
【解析】
【分析】由抛物线的图象可判断a、b、c的符号,可判断①;由x=-1和x=2时对应的函数值可判断②、③;由对称轴可得b=-2a分别代入a-b+c,借助函数图象可判断④;可以比较当x=m和x=1时的函数值的大小可判断⑤,可求得答案.
【详解】解:∵图象开口向下,与y轴的交点在x轴的上方,
∴a<0,c>0,
∵对称轴为x=1,
∴,
∴b=-2a>0,
∴abc<0,故①错误;
当x=-1时,可知y<0,
∴a-b+c<0,
∴a+c<b,故②错误;
∵抛物线与x的一个交点在-1和0之间,
∴另一个交点在2和3之间,
∴当x=2时,y>0,
∴4a+2b+c>0,故③正确;
∵b=-2a,
∴a=,且a-b+c<0,
∴,
即,
∴2c<3b,故④正确;
∵抛物线开口向下,
∴当x=1时,y有最大值,
∴a+b+c>am2+bm+c,
∴a+b>m(am+b),故⑤正确;
综上可知正确的有3个,
故选:B.
【点评】本题主要考查二次函数图象与系数的关系,掌握y=ax2+bx+c(a≠0)中各系数与其图象的关系是解题的关键.
填空题(每小题3分,共15分)
11 .把二次函数y=x2﹣2x+3的图象绕原点旋转180°后得到的图象的函数解析式为_____.
【答案】y=﹣x2﹣2x﹣3
【解析】
【分析】求出原抛物线的顶点坐标以及绕原点旋转180°后的抛物线的顶点坐标,再根据旋转后抛物线开口方向向下,利用顶点式解析式写出即可.
【详解】∵抛物线y=x2﹣2x+3=(x﹣1)2+1的顶点坐标为(1,1),
∴绕原点旋转180°后的抛物线的顶点坐标为(﹣1,﹣1),
∴所得到的图象的解析式为y=﹣(x+1)2﹣1,即y=﹣x2﹣2x﹣3.
故答案为y=﹣x2﹣2x﹣3.
【点评】本题考查了二次函数图象与几何变换,利用顶点的变化确定函数解析式的变化更简便.
12 .由于被墨水污染,一道数学题仅能见到如下文字:已知二次函数y=ax2+bx+c的图象过点(1,0)……,求证:这个二次函数的图象关于直线x=2对称,根据现有信息,得出有关这个二次函数的下列结论:①过点(3,0);②顶点(2,2);③在x轴上截得的线段的长是2;④与y轴的交点是(0,3),其中正确的是______(填序号).
【答案】①③
【解析】
【分析】利用抛物线的对称性得到抛物线与轴的另一个交点坐标为,从而得到抛物线在轴上截得的线段的长,利用和对称轴方程不能确定顶点的纵坐标和的值.
【详解】二次函数的图象过点,对称轴为直线,
抛物线与轴的另一个交点坐标为,
抛物线在轴上截得的线段的长是.
故答案为:①③.
【点评】本题考查了抛物线与轴的交点:把求二次函数(,,是常数,)与轴的交点坐标问题转化解.关于的一元二次方程即可求得交点横坐标.
13 .飞机着陆后滑行的距离s(单位:m)关于滑行的时间t(单位:s)的函数解析式是s=60t -1.2t 2,飞机着陆后滑行______秒才能停下来.
【答案】25
【解析】
【分析】将函数解析式配方成顶点式求出s取得最大值时的t的值即可得.
【详解】解:∵s=60t-1.2t2=-1.2(t-25)2+750,
∴当t=25时,s取得最大值750,
即飞机着陆后滑行25秒才能停下来,
故答案为:25.
【点评】本题主要考查二次函数的应用,理解题意得出飞机滑行的距离即为s的最大值是解题的关键.
14 .函数y=ax2﹣2ax+m(a>0)的图象过点(2,0),那么使函数值y<0成立的x的取值范围是______.
【答案】
【解析】
【分析】先求出抛物线的对称轴,由抛物线与x轴的交点(2,0)和对称轴就可以求出抛物线与x轴的另一个交点坐标,又因为抛物线开口向上,所以在x轴下方部分,,由抛物线与x轴两交点的横坐标,就可以求解.
【详解】解:∵函数
函数图像开口向上,对称轴x= -=1.
∵图像经过点(2,0),2-1=1,1-1=0
∴抛物线与x轴的另一个交点为即(0,0),在x轴下方部分,,
故当 时,.
【点评】本题考查抛物线的对称性,解答关键是由对称轴、抛物线与求出x轴的交点(2,0),求出抛物线与x轴的另一个交点坐标.
15.二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(,﹣2);⑤当x<时,y随x的增大而减小;⑥a+b+c>0中,正确的有______.(只填序号)
【答案】①②③⑤
【解析】
【分析】根据图象可判断①②③④⑤,由x=1时,y<0,可判断⑥.
【详解】由图象可得,a>0,c<0,b<0,△=b2﹣4ac>0,对称轴为x=,
∴abc>0,4ac<b2,当时,y随x的增大而减小.故①②⑤正确,
∵,
∴2a+b>0,
故③正确,
由图象可得顶点纵坐标小于﹣2,则④错误,
当x=1时,y=a+b+c<0,故⑥错误.
故答案为:①②③⑤.
【点评】本题考查的是二次函数图象与系数的关系,二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.
解答题(共8小题,75分)
16 .(8分)已知二次函数y=x2﹣4x+3.
(1)求该二次函数与x轴的交点坐标和顶点;
(2)在所给坐标系中画出该二次函数的大致图象,并写出当y<0时,x的取值范围.
【答案】(1)二次函数与x轴的交点坐标为(1,0)(3,0),抛物线的顶点坐标为(2,﹣1);
(2)图见详解;当y<0时,1<x<3.
【解析】
【分析】(1)令y=0,可求出x的值,即为与x轴的交点坐标;将二次函数化为顶点式即可得出顶点坐标
(2)根据与x轴的交点坐标,顶点坐标,与y轴的交点即可画出图像,再根据图像信息即可得出x的取值范围.
【详解】(1)当y=0时,x2﹣4x+3=0,解得x1=1,x2=3,
所以该二次函数与x轴的交点坐标为(1,0)(3,0);
因为y=x2﹣4x+3=x2﹣4x+4﹣1=(x﹣2)2﹣1,
所以抛物线顶点坐标为(2,﹣1);
(2)函数图象如图:
由图象可知,当y<0时,1<x<3.
【点评】本题考查了二次函数的图像及性质,熟练掌握二次函数的顶点式是解题的关键.
(8分)为了改善小区环境,某小区决定要在一块边靠墙(墙长18m)的空地,修建一个矩形绿地ABCD,绿地一边靠墙,另三边用总长为40m的栅栏围住(如图),设AB边为xm,绿地面积为ym2.
(1)求y与x之间函数关系,并求出自变量x的取值范围;
(2)绿地的面积能不能为200m2?如果能,求出x的值,如果不能,请说明理由.
【答案】(1)y与x之间的函数关系式是y=﹣2x2+40x(0<x<20);(2)绿化带的面积不能为200m2,理由见解析.
【解析】
【分析】(1)根据题意可以列出y与x之间的函数关系式并写出x的取值范围;
(2)先判断绿化带的面积能不能为200m2,然后说明理由即可解答本题.
【详解】(1) 由题意可得:y=x (40﹣2x)=﹣2x2+40x,
即y与x之间的函数关系式是y=﹣2x2+40x(0<x<20);
(2)绿化带的面积不能为200m2.理由如下:
将y=200代入y=﹣2x2+40x得:
200=﹣2x2+40x,
解得:x=10,
∴BC=40﹣2x=20>18,
∴绿化带面积不能为200m2.
【点评】本题考查了二次函数的应用、一元二次方程的应用,解答本题的关键是根据题意,列出相应的函数关系式和一元二次方程.
18 .(9分)某超市销售一种水果,进价为每箱40元,规定售价不低于进价.现在的售价为每箱72元,每月可销售60箱.经市场调查发现:若这种水果的售价每降低2元,则每月的销量将增加10箱,设每箱水果降价x元(x为偶数),每月的销量为y箱.
(1)写出y与x之间的函数关系式和自变量x的取值范围.
(2)若该超市在销售过程中每月需支出其他费用500元,则如何定价才能使每月销售水果的利润最大?最大利润是多少元?
【答案】(1)y=60+5x,(0≤x≤32,且x为偶数);(2)售价为62元时,每月销售水果的利润最大,最大利润是1920元.
【解析】
【分析】(1)根据价格每降低2元,平均每月多销售10箱,由每箱降价元,多卖,据此可以列出函数关系式;
(2)由利润=(售价 成本)×销售量 每月其他支出列出函数关系式,求出最大值.
【详解】解:(1)根据题意知y=60+5x,(0≤x≤32,且x为偶数);
(2)设每月销售水果的利润为w,
则w=(72﹣x﹣40)(5x+60)﹣500
=﹣5x2+100x+1420
=﹣5(x﹣10)2+1920,
当x=10时,w取得最大值,最大值为1920元,
答:当售价为62元时,每月销售水果的利润最大,最大利润是1920元.
【点评】本题主要考查二次函数的应用,由利润=(售价 成本)×销售量列出函数关系式求最值,用二次函数解决实际问题是解题的关键.
19 .(8分)某电商在购物平台上销售一款小电器,其进价为45元/件,每销售一件需缴纳平台推广费5元,该款小电器每天的销售量y(件)与每件的销售价格x(元)满足函数关系:y=﹣2x+200.为保证市场稳定,供货商规定销售价格不得低于75元/件.
(1)写出每天的销售利润w(元)与销售价格x(元)的函数关系式(不必写出x的取值范围);
(2)每件小电器的销售价格定为多少元时,才能使该款小电器每天获得的利润是1200元?
【答案】(1)w=﹣2x2+300x﹣10000;(2)每件小电器的销售价格定为80元时,才能使该款小电器每天获得的利润是1200元.
【解析】
【分析】(1)直接利用销量×每件的利润=总利润进而得出函数关系式;
(2)利用总利润=1200,进而解方程得出答案.
【详解】(1)由题意可得:w=(x﹣50)(﹣2x+200)=﹣2x2+300x﹣10000;
(2)由题意可得:1200=﹣2x2+300x﹣10000,
解得:x1=70(不合题意舍去),
x2=80,
答:每件小电器的销售价格定为80元时,才能使该款小电器每天获得的利润是1200元.
【点评】此题主要考查了一元二次方程的应用以及二次函数的应用,正确得出函数关系式是解题关键.
20 .(8分)已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点为(0,3).
(1)求此二次函数的解析式;
(2)结合函数图象,直接写出当y≤﹣1时x的取值范围.
【答案】(1)y=﹣x2+2x+3(2)当x≤1﹣或x≥1+时,y≤﹣1
【解析】
【分析】(1)利用待定系数法求抛物线解析式;
(2)先计算出y=-1对应的自变量的值,然后结合图象,写出y≤﹣1所对应的自变量的范围即可.
【详解】(1)把(-1,0)和(0,3)代入y=﹣x2+bx+c得:,解得:,所以抛物线解析式为y=﹣x2+2x+3;
(2)当y=-1时,﹣x2+2x+3=-1,解得:x1=1,x2=1,当x≤1或x≥1时,y≤﹣1.
【点评】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化解关于x的一元二次方程即可求得交点横坐标.也考查了二次函数的性质.
21 .(9分)请阅读下列材料,并完成相应的任务:
定义:我们把自变量为的二次函数与(,)称为一对“亲密函数”,如的“亲密函数”是.
任务:
(1)写出二次函数的“亲密函数”:______;
(2)二次函数的图像与轴交点的横坐标为1和,它的“亲密函数”的图像与轴交点的横坐标为______,猜想二次函数()的图像与轴交点的横坐标与其“亲密函数”的图像与轴交点的横坐标之间的关系是______;
(3)二次函数的图像与轴交点的横坐标为1和,请利用(2)中的结论直接写出二次函数的图像与轴交点的横坐标.
【答案】(1);(2)4和-1;互为相反数;(3)二次函数的图像与轴交点的横坐标为和
【分析】(1)根据二次函数的“亲密函数”定义把一次项系数变为相反数即可;
(2)利用“亲密函数”建立y=0时方程,解方程,得出“亲密函数”与x轴交点横坐标,与原函数与x轴交点横坐标比较,得出规律即可;
(3)先将函数变形,发现与“亲密函数”类似,根据原函数与x轴交点横坐标得出“亲密函数”与x轴交点横坐标,利用2x等于交点横坐标,求出x得出所求函数与x轴的交点横坐标即可.
【详解】解:(1)二次函数的“亲密函数”为,
故答案为:;
(2),解得,
它的“亲密函数”的图像与轴交点的横坐标为4和-1,
∴二次函数()的图像与轴交点的横坐标与其“亲密函数”的图像与轴交点的横坐标之间的关系是互为相反数;
故答案为4和-1;互为相反数;
(3),
∵二次函数的图像与轴交点的横坐标为1和,
∴二次函数的图像与轴交点的横坐标为-1和,
∴图像与轴交点的横坐标为-1和,
∴2x=-1,2x=2021,
∴,,
∴二次函数的图像与轴交点的横坐标为和.
【点评】本题考查新定义函数,仔细阅读题目,抓住实质,抛物线与x轴交点横坐标和一元二次方程的根,利用“亲密函数”变形得出新函数图像与x轴的交点横坐标是解题关键.
22 .(12分)已知抛物线的对称轴是直线,与轴相交于A,B两点(点B在点A右侧),与轴交于点C.
(1)求抛物线的解析式;
(2)如图,若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),是否存在点P,使四边形的面积最大?若存在,求点P的坐标及四边形面积的最大值;若不存在,请说明理由.
【思路点拨】
(1)根据对称轴公式,求出的值即可;
(2)连接,过点作轴交于点,设,再表示出,表示出的长,根据表示出,再根据二次函数求出最大值及的坐标,再根据即可.
【解题过程】
(1)解:抛物线的对称轴是直线,
,解得,
故抛物线的解析式为.
(2)解:连接,过点作轴交于点,设,
时,,
解得:,,,
,
设直线的解析式为,代入,,
得,解得:,
∴直线的解析式为,
,
∴,
,
当时,有最大值,最大值为,此时,
又,
故存在点,使四边形的面积最大,最大值为.
23.(13分)在平面直角坐标系中,抛物线经过点A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求该抛物线的函数表达式及顶点C的坐标;
(2)设该抛物线上一动点P的横坐标为t.
①在图1中,当﹣3<t<0时,求△PBO的面积S与t的函数关系式,并求S的最大值;
②在图2中,若点P在该抛物线上,点E在该抛物线的对称轴上,且以A,O,P,E为顶点的四边形是平行四边形,求点P的坐标;
【分析】(1)由待定系数法求函数的解析式即可;
(2)①求出直线BO的解析式,过点P作PG⊥x轴交BO于点G,可得E(t,﹣t)再由S(t)2,即可求解;
②设E(﹣1,m),根据平行四边形对角线的情况,分三种情况讨论:当AO为平行四边形的对角线时,当AP为平行四边形的对角线时,当AE为平行四边形的对角线时;利用中点坐标公式求解即可;
【解答】解:(1)设抛物线的解析式为y=ax2+bx,
将A(﹣2,0),B(﹣3,3)代入,
∴,
解得,
∴y=x2+2x,
∴C(﹣1,﹣1);
(2)①∵P的横坐标为t,
∴P(t,t2+2t),
设直线BO的解析式为y=kx,
∴﹣3k=3,
∴k=﹣1,
∴y=﹣x,
过点P作PG⊥x轴交BO于点G,
∴E(t,﹣t)
∴PG=﹣t﹣t2﹣2t=﹣t2﹣3t,
∴S3×(﹣t2﹣3t)(t)2,
∵﹣3<t<0,
∴t时,S有最大值;
②∵y=x2+2x,
∴抛物线的对称轴为直线x=﹣1,
设E(﹣1,m),
当AO为平行四边形的对角线时,
,
解得,
∴P(﹣1,﹣1);
当AP为平行四边形的对角线时,
,
解得,
∴P(1,3);
当AE为平行四边形的对角线时,
,
解得,
∴P(﹣3,3);
综上所述:P点坐标为(﹣1,﹣1)或(1,3)或(﹣3,3);
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
