人教版数学八年级上册 11.2.2 三角形的外角 课件(共22张PPT)
文档属性
| 名称 | 人教版数学八年级上册 11.2.2 三角形的外角 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-12 10:18:35 | ||
图片预览




文档简介
(共22张PPT)
人教版 数学 七年级 上册
第十一章 三角形
11.2.2 三角形的外角
目录
CONTENTS
1
2
自主学习
全程探究
3
4
全员提高
自我评价
PART 01自主学习
(一)
学习目标
1. 理解并掌握三角形的外角的概念,能够在复杂图形中找出外角.
2. 掌握三角形的一个外角等于与它不相邻的两个内角的和及三角形的内角和.
3. 会利用三角形的外角性质解决问题.
PART 01自主学习
(二)
自学检测
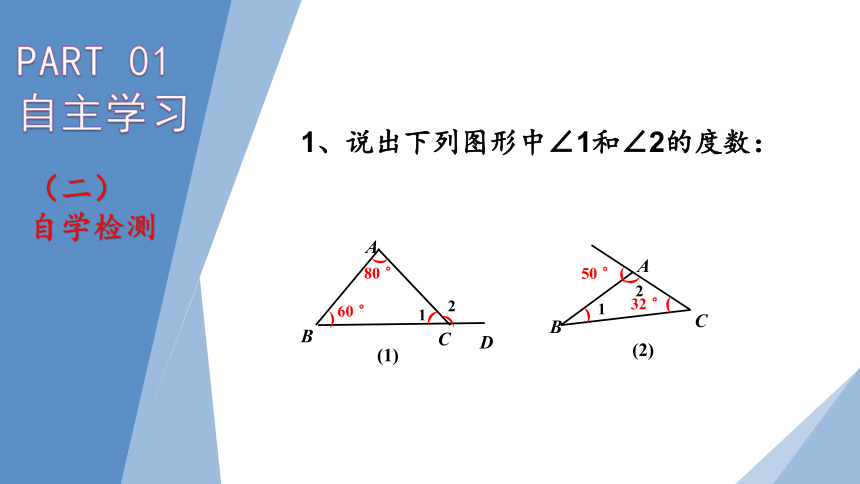
1、说出下列图形中∠1和∠2的度数:
A
B
C
D
(
(
(
80 °
60 °
(
2
1
(1)
A
B
C
(
(
(
(
2
1
50 °
32 °
(2)
PART 01自主学习
(二)
自学检测
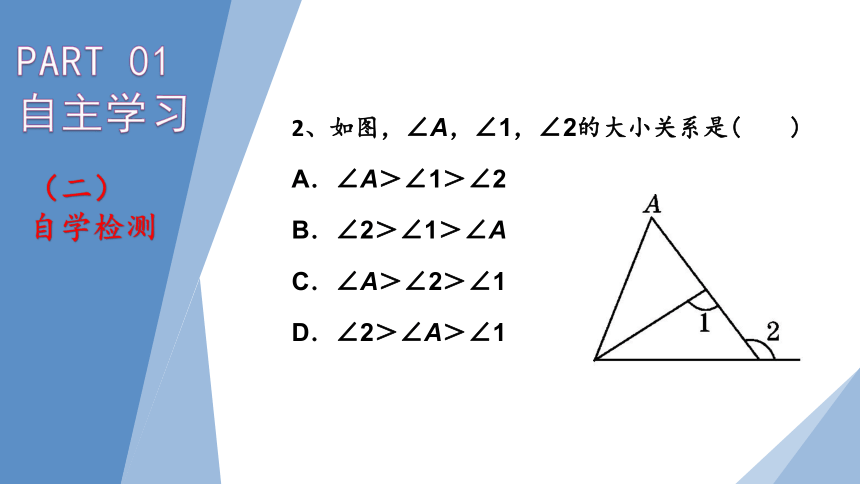
2、如图,∠A,∠1,∠2的大小关系是( )
A.∠A>∠1>∠2
B.∠2>∠1>∠A
C.∠A>∠2>∠1
D.∠2>∠A>∠1
PART 02全程探究
探究一:
三角形的外角的概念
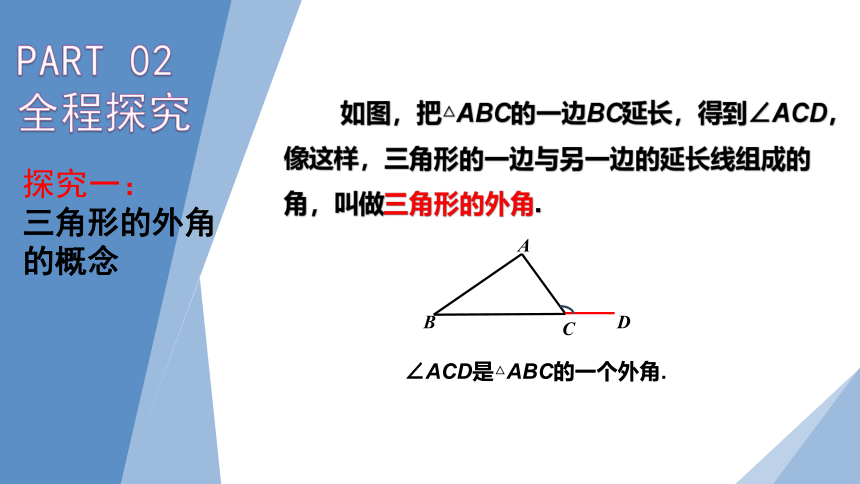
如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
∠ACD是△ABC的一个外角.
C
B
A
D
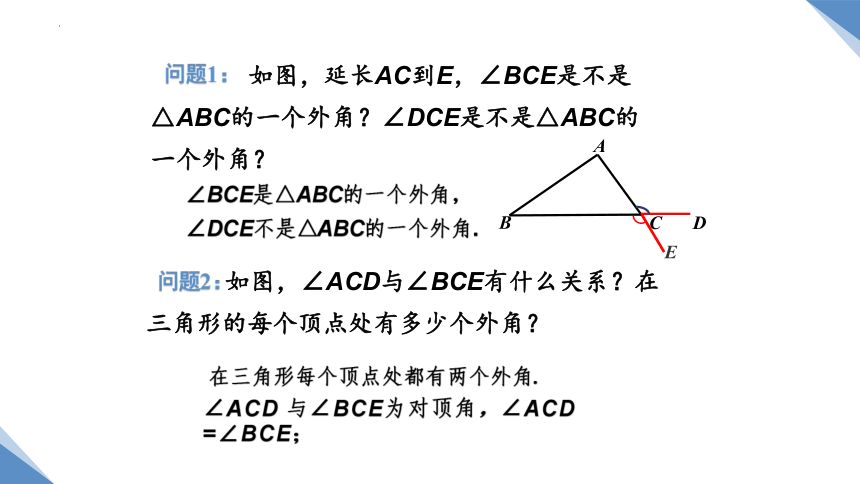
如图,延长AC到E,∠BCE是不是△ABC的一个外角?∠DCE是不是△ABC的一个外角?
E
在三角形每个顶点处都有两个外角.
∠ACD 与∠BCE为对顶角,∠ACD =∠BCE;
C
B
A
D
∠BCE是△ABC的一个外角,∠DCE不是△ABC的一个外角.
如图,∠ACD与∠BCE有什么关系?在三角形的每个顶点处有多少个外角?
问题1:
问题2:
F
A
B
C
D
E
例1 如图,∠ BEC是哪个三角形的外角?∠AEC是哪个三角形的外角?∠EFD是哪个三角形的外角?
∠BEC是△AEC的外角;
∠AEC是△BEC的外角;
∠EFD是△BEF和△DCF的外角.
答:
PART 02全程探究
探究二:
三角形的外角的性质
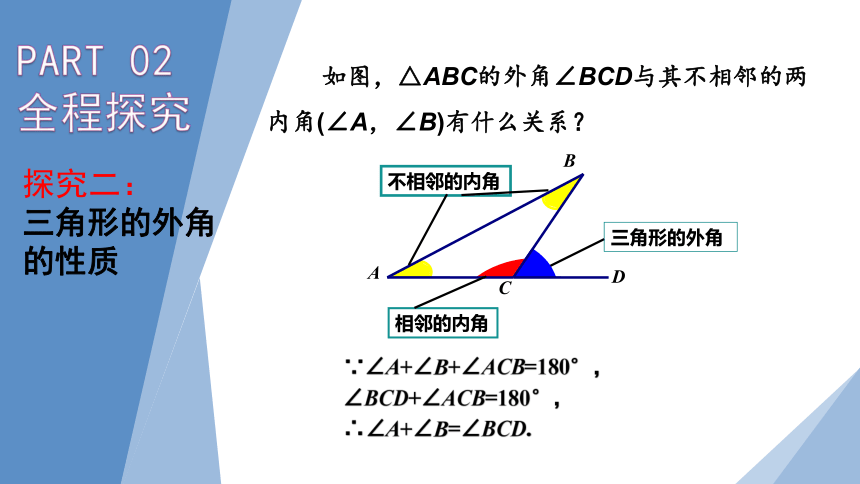
如图,△ABC的外角∠BCD与其不相邻的两内角(∠A,∠B)有什么关系?
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
∵∠A+∠B+∠ACB=180°,∠BCD+∠ACB=180°,
∴∠A+∠B=∠BCD.
A
B
C
D
(
(
(
三角形的外角等于与它不相邻的两个内角的和.
∵ ∠ACD是△ABC的一个外角.
∴ ∠ACD= ∠A+ ∠B.
例2 如图,∠A=42°,∠ABD=28°,∠ACE=18°,求∠BFC的度数.
∵ ∠BEC是△AEC的一个外角,
∴ ∠BEC= ∠A+ ∠ACE,
∵∠A=42° ,∠ACE=18°,
∴ ∠BEC=60°.
∵ ∠BFC是△BEF的一个外角,
∴ ∠BFC= ∠ABD+ ∠BEF,
∵ ∠ABD=28° ,∠BEC=60°,
∴ ∠BFC=88°.
解:
F
A
C
D
E
B
分析:根据平行线的性质求出∠C,
再根据三角形外角性质即可求出∠3.
解: ∵AB∥CD,∠1=45°,∴∠C=∠1=45°.
又∵∠2=35°,
∴∠3=∠2+∠C=35°+45°=80°.
例3 如图,直线AB,CD被BC 所截,若AB∥CD,∠1=45°,∠2=35°, 则∠3=________度.
80
PART 02全程探究
探究三:
三角形的外角和定理
如图, ∠BAE, ∠CBF, ∠ACD是△ABC的三个外角,它们的和是多少?
解:由三角形的一个外角等于与它不相邻的两个内角的和,得
∠BAE= ∠2+ ∠3,
∠CBF= ∠1+ ∠3,
∠ACD= ∠1+ ∠2.
又知∠1+ ∠2+ ∠3=180 °,
所以∠BAE+ ∠CBF+ ∠ACD
=2(∠1+ ∠2+ ∠3)=360 °.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
解法二:过A作AM平行于BC,
∠3= ∠4
B
C
1
2
3
4
A
∠2= ∠BAM,
所以 ∠1+ ∠2+ ∠3= ∠1+ ∠4+ ∠BAM=360°
M
∠2+ ∠ 3= ∠ 4+∠BAM,
结论:三角形的外角和等于360°.
D
E
F
PART 03全员提高
(一)统一观点
PART 03全员提高
(二)课堂检测
1、下列对三角形的外角和叙述正确的是( )
A.三角形的外角和等于180°
B.三角形的外角和就是所有外角的和
C.三角形的外角和等于所有外角和的一半
D.以上都不对
PART 03全员提高
(二)课堂检测
2、如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
A.40° B.45° C.50° D.55°
PART 03全员提高
(二)课堂检测
3、 如图,点D在△ABC边AB的延长线上,DE∥BC.若∠A=35°,∠C=24°,则∠D的度数是( )
A.24° B.59° C.60° D.69°
PART 03全员提高
(二)课堂检测
4、(1)如图,∠BDC是________的外角,也是 的外角;
(2)若∠B=45 °,∠BAE=36 °,∠BCE=20 °,试求∠AEC的度数.
A
B
C
D
E
PART 03全员提高
(二)课堂检测
5、如图,试求出∠A+∠B+∠C+∠D+∠E+∠F
=________.
1
2
3
B
A
C
P
N
M
F
PART 04自我评价
这节课我学到了什么?
我还有什么疑问?
01
02
课后反思
谢谢大家!
人教版 数学 七年级 上册
第十一章 三角形
11.2.2 三角形的外角
目录
CONTENTS
1
2
自主学习
全程探究
3
4
全员提高
自我评价
PART 01自主学习
(一)
学习目标
1. 理解并掌握三角形的外角的概念,能够在复杂图形中找出外角.
2. 掌握三角形的一个外角等于与它不相邻的两个内角的和及三角形的内角和.
3. 会利用三角形的外角性质解决问题.
PART 01自主学习
(二)
自学检测
1、说出下列图形中∠1和∠2的度数:
A
B
C
D
(
(
(
80 °
60 °
(
2
1
(1)
A
B
C
(
(
(
(
2
1
50 °
32 °
(2)
PART 01自主学习
(二)
自学检测
2、如图,∠A,∠1,∠2的大小关系是( )
A.∠A>∠1>∠2
B.∠2>∠1>∠A
C.∠A>∠2>∠1
D.∠2>∠A>∠1
PART 02全程探究
探究一:
三角形的外角的概念
如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
∠ACD是△ABC的一个外角.
C
B
A
D
如图,延长AC到E,∠BCE是不是△ABC的一个外角?∠DCE是不是△ABC的一个外角?
E
在三角形每个顶点处都有两个外角.
∠ACD 与∠BCE为对顶角,∠ACD =∠BCE;
C
B
A
D
∠BCE是△ABC的一个外角,∠DCE不是△ABC的一个外角.
如图,∠ACD与∠BCE有什么关系?在三角形的每个顶点处有多少个外角?
问题1:
问题2:
F
A
B
C
D
E
例1 如图,∠ BEC是哪个三角形的外角?∠AEC是哪个三角形的外角?∠EFD是哪个三角形的外角?
∠BEC是△AEC的外角;
∠AEC是△BEC的外角;
∠EFD是△BEF和△DCF的外角.
答:
PART 02全程探究
探究二:
三角形的外角的性质
如图,△ABC的外角∠BCD与其不相邻的两内角(∠A,∠B)有什么关系?
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
∵∠A+∠B+∠ACB=180°,∠BCD+∠ACB=180°,
∴∠A+∠B=∠BCD.
A
B
C
D
(
(
(
三角形的外角等于与它不相邻的两个内角的和.
∵ ∠ACD是△ABC的一个外角.
∴ ∠ACD= ∠A+ ∠B.
例2 如图,∠A=42°,∠ABD=28°,∠ACE=18°,求∠BFC的度数.
∵ ∠BEC是△AEC的一个外角,
∴ ∠BEC= ∠A+ ∠ACE,
∵∠A=42° ,∠ACE=18°,
∴ ∠BEC=60°.
∵ ∠BFC是△BEF的一个外角,
∴ ∠BFC= ∠ABD+ ∠BEF,
∵ ∠ABD=28° ,∠BEC=60°,
∴ ∠BFC=88°.
解:
F
A
C
D
E
B
分析:根据平行线的性质求出∠C,
再根据三角形外角性质即可求出∠3.
解: ∵AB∥CD,∠1=45°,∴∠C=∠1=45°.
又∵∠2=35°,
∴∠3=∠2+∠C=35°+45°=80°.
例3 如图,直线AB,CD被BC 所截,若AB∥CD,∠1=45°,∠2=35°, 则∠3=________度.
80
PART 02全程探究
探究三:
三角形的外角和定理
如图, ∠BAE, ∠CBF, ∠ACD是△ABC的三个外角,它们的和是多少?
解:由三角形的一个外角等于与它不相邻的两个内角的和,得
∠BAE= ∠2+ ∠3,
∠CBF= ∠1+ ∠3,
∠ACD= ∠1+ ∠2.
又知∠1+ ∠2+ ∠3=180 °,
所以∠BAE+ ∠CBF+ ∠ACD
=2(∠1+ ∠2+ ∠3)=360 °.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
解法二:过A作AM平行于BC,
∠3= ∠4
B
C
1
2
3
4
A
∠2= ∠BAM,
所以 ∠1+ ∠2+ ∠3= ∠1+ ∠4+ ∠BAM=360°
M
∠2+ ∠ 3= ∠ 4+∠BAM,
结论:三角形的外角和等于360°.
D
E
F
PART 03全员提高
(一)统一观点
PART 03全员提高
(二)课堂检测
1、下列对三角形的外角和叙述正确的是( )
A.三角形的外角和等于180°
B.三角形的外角和就是所有外角的和
C.三角形的外角和等于所有外角和的一半
D.以上都不对
PART 03全员提高
(二)课堂检测
2、如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
A.40° B.45° C.50° D.55°
PART 03全员提高
(二)课堂检测
3、 如图,点D在△ABC边AB的延长线上,DE∥BC.若∠A=35°,∠C=24°,则∠D的度数是( )
A.24° B.59° C.60° D.69°
PART 03全员提高
(二)课堂检测
4、(1)如图,∠BDC是________的外角,也是 的外角;
(2)若∠B=45 °,∠BAE=36 °,∠BCE=20 °,试求∠AEC的度数.
A
B
C
D
E
PART 03全员提高
(二)课堂检测
5、如图,试求出∠A+∠B+∠C+∠D+∠E+∠F
=________.
1
2
3
B
A
C
P
N
M
F
PART 04自我评价
这节课我学到了什么?
我还有什么疑问?
01
02
课后反思
谢谢大家!
