2022-2023学年江苏省镇江重点中学高二(下)期末数学试卷(含解析)
文档属性
| 名称 | 2022-2023学年江苏省镇江重点中学高二(下)期末数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 650.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-11 16:05:21 | ||
图片预览




文档简介
2022-2023学年江苏省镇江重点中学高二(下)期末数学试卷
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 复数,则( )
A. B. C. D.
2. 的展开式中常数项为( )
A. B. C. D.
3. 已知等差数列满足,,其前项和为,则使成立时最大值为( )
A. B. C. D.
4. 袋中装有个红球和个白球,不放回地一次摸出一个,在第一次摸出红球的条件下,第二次摸到红球的概率为( )
A. B. C. D.
5. 已知函数的图象关于直线对称,则函数的单调递增区间为( )
A. B. C. D.
6. 如图是梁思成研究广济寺三大士殿的手稿,它是该建筑中垂直于房梁的截面,其中是房梁与该截面的交点,,分别是两房檐与该截面的交点,该建筑关于房梁所在铅垂面垂直于水平面的面对称,测得柱子与之间的距离是为测量单位,柱子与之间的距离是如果把,视作线段,记,,是的四等分点,,,是的四等分点,若,则线段的长度为( )
A. B. C. D.
7. ,是椭圆上两点,线段的中点在直线上,则直线与轴的交点的纵坐标的取值范围是( )
A. B.
C. D.
8. 在概率论中,全概率公式指的是:设为样本空间,若事件,,,两两互斥,,则对任意的事件,有若甲盒中有个白球、个红球、个黑球,乙盒中有个白球、个红球、个黑球,现从甲盒中随机取出一个球放入乙盒,再从乙盒中随机取出一个球,若从甲盒中取出的球和从乙盒中取出的球颜色相同的概率大于等于,则的最大值为( )
A. B. C. D.
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
9. 如图,矩形中,、分别为、的中点,且,现将沿问上翻折,使点移到点,则在翻折过程中,下列结论正确的是( )
A. 存在点,使得
B. 存在点,使得
C. 三棱锥的体积最大值为
D. 当三棱锥的体积达到最大值时,三棱锥外接球表面积为
10. 为比较甲,乙两地某月时的气温,随机选取该月中的天,将这天中时的气温数据单位:制成如图所示的茎叶图,考虑以下结论中根据茎叶图能得到的统计结论的为( )
A. 甲地该月时的平均气温低于乙地该月时的平均气温
B. 甲地该月时的平均气温高于乙地该月时的平均气温
C. 甲地该月时的气温的标准差小于乙地该月时的气温的标准差
D. 甲地该月时的气温的标准差大于乙地该月时的气温的标准差
11. 已知数列的前项和为,且,,则( )
A. B.
C. 数列是递增数列 D. 数列的最小值为
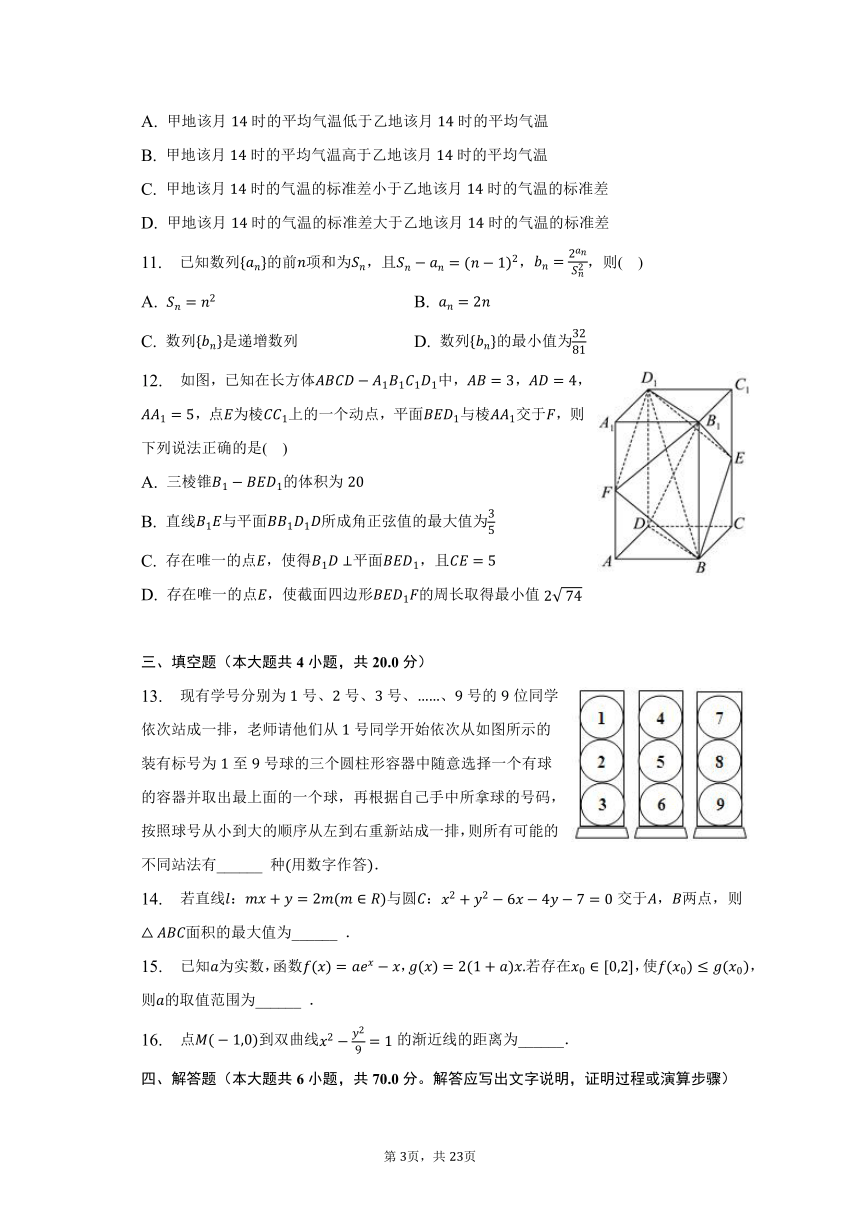
12. 如图,已知在长方体中,,,,点为棱上的一个动点,平面与棱交于,则下列说法正确的是( )
A. 三棱锥的体积为
B. 直线与平面所成角正弦值的最大值为
C. 存在唯一的点,使得平面,且
D. 存在唯一的点,使截面四边形的周长取得最小值
三、填空题(本大题共4小题,共20.0分)
13. 现有学号分别为号、号、号、、号的位同学依次站成一排,老师请他们从号同学开始依次从如图所示的装有标号为至号球的三个圆柱形容器中随意选择一个有球的容器并取出最上面的一个球,再根据自己手中所拿球的号码,按照球号从小到大的顺序从左到右重新站成一排,则所有可能的不同站法有______ 种用数字作答.
14. 若直线:与圆:交于,两点,则面积的最大值为______ .
15. 已知为实数,函数,若存在,使,则的取值范围为______ .
16. 点到双曲线的渐近线的距离为______.
四、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
已知与都是正项数列,的前项和为,,且满足,等比数列满足,.
求数列,的通项公式;
记数列的前项和为,求满足不等式的自然数的最小值.
18. 本小题分
在贯彻中共中央、国务院关于精准扶贫政策的过程中,某单位在某市定点帮扶甲、乙两村各户贫困户.为了做到精准帮扶,工作组对这户村民的年收入情况、劳动能力情况.子女受教育情况、危旧房情况、患病情况等进行调查.并把调查结果转化为各户的贫困指标将指标按照,,,,分成五组,得到如图所示的频率分布直方图.规定若,则认定该户为“绝对贫困户”,否则认定该户为“相对贫困户”,且当时,认定该户为“低收入户”;当时,认定该户为“亟待帮助户“已知此次调查中甲村的“绝对贫困户”占甲村贫困户的.
完成下面的列联表,并判断是否有的把握认为绝对贫困户数与村落有关:
甲村 乙村 总计
绝对贫困户
相对贫困户
总计
某干部决定在这两村贫困指标处于的贫困户中,随机选取户进行帮扶,用表示所选户中“亟待帮助户”的户数,求的分布列和数学期望.
附:,其中.
19. 本小题分
已知函数.
Ⅰ求的极值;
Ⅱ已知,且对任意的恒成立,求的最大值;
Ⅲ设的零点为,当,,且时,证明:.
20. 本小题分
如图,平面,,分别是,中点,,.
求二面角的余弦值;
点是线段上的动点,当直线与所成的角最小时,求线段的长.
21. 本小题分
沿海某市为了进一步完善海防生态防护体系,林业部门计划在沿海新建防护林万亩,从年开始,每年春季在规划的区域内植树造林,第一年植树亩,以后每一年比上一年多植树亩,假设所植树木全部成活.
Ⅰ求到哪一年春季新建防护林计划全部完成;
Ⅱ若每亩新植树苗的木材量为立方米,且所植树木每一年从春季开始生长,到年底停止生长时木材量的年自然增长率为,到新建防护林计划全部完成的那一年底,新建防护林的木材总量为多少立方米参考数据:
22. 本小题分
已知椭圆的离心率为,且经过点,一条直线与椭圆交于,两点,以为直径的圆经过坐标原点.
Ⅰ求椭圆的标准方程;
Ⅱ求证:为定值.
答案和解析
1.【答案】
【解析】解:复数,
则,
故选:.
利用复数的运算法则、共轭复数的定义即可得出.
本题考查了复数的运算法则、共轭复数的定义,属于基础题.
2.【答案】
【解析】
【分析】
本题考查了二项式定理的应用,属于中档题.
由的通项公式,即可得解.
【解答】
解:由的通项公式,
当即时,,
当即时,,
的展开式中常数项.
故选:.
3.【答案】
【解析】解:等差数列的首项,,,
,.
于是,
.
使成立的最大正整数是.
故选:.
差数列的首项,,,可得,再利用求和公式及其性质即可得出..
本题考查了等差数列的通项公式求和公式及其性质,考查了推理能力与计算能力,属于中档题.
4.【答案】
【解析】解:袋中装有个红球和个白球,不放回地一次摸出一个,
第一次摸到红球,
第二次摸球时袋中有个红球和个白球,
第二次摸到红球的概率为.
故选:.
第一次摸到红球,第二次摸球时袋中有个红球和个白球,由此能求出第二次摸到红球的概率.
本题考查概率的求法,是中档题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.
5.【答案】
【解析】解:函数的图象关于直线对称,
,即,
即,
.
,.
由于为开口向下的抛物线,其对称轴为,定义域为,
它的递增区间为,
由复合函数的单调性知,
的单调递增区间为,
故选:.
函数的图象关于直线对称,可求得,利用复合函数的单调性解求得答案.
本题考查利用导数研究函数的单调性,突出考查复合函数的单调性的应用,考查推理与运算能力,属于中档题.
6.【答案】
【解析】解:根据题意作出示意图,如图所示,其中点与点重合,
该建筑关于房梁所在铅垂面垂直于水平面的面对称,
又,,是的四等分点,,,是的四等分点,
,,,,,
为直角三角形,四边形为矩形,
,且,,
又,,
,
,
.
故选:.
画出平面图形,数形结合,根据余弦定理,即可求解.
本题考查两点间距离的求解,余弦定理的应用,方程思想,化归转化思想,属中档题.
7.【答案】
【解析】解:由题意可知,直线的斜率必然存在,设直线的方程为,
则直线与轴的交点的纵坐标为,设点,,
将直线的方程与椭圆方程联立并化简得,,
化简得,即.
由韦达定理可得,所以,
将等式两边平方得,所以.
当且仅当时,等号成立,由于,解得或.
因此,直线与轴的交点的纵坐标的取值范围是.
故选:.
设直线的方程为,点,,联立直线与椭圆的方程,根据判别式与韦达定理求解的范围即可.
本题主要考查椭圆的性质,直线与椭圆的综合,考查运算求解能力,属于中档题.
8.【答案】
【解析】
【分析】
本题考查全概率公式,属于中档题.
分别求出两次取出的球都是白球的概率,两次取出的球都是红球的概率,两次取出的球都是黑球的概率,将他们加起来得,再解不等式,即可得到结果.
【解答】
解:两次取出的球都是白球的概率;
两次取出的球都是红球的概率;
两次取出的球都是黑球的概率;
两次取出的球的颜色相同的概率,
则,解得,
则的最大值为.
故选C.
9.【答案】
【解析】解:对于,,,因此,不平行,
即不存在点,使得故A错误;
对于,如图:
取的中点,连接,,,,当时,
因为,即则,
而,,平面,
又,分别为,的中点,
即,于是平面,而平面,
则,故B正确;
对于,在翻折过程中,令与平面所成角为,
则点到平面的距离 ,
又的面积为,
因此三棱锥的体积为:,
当且仅当时,即平面时取等号,
所以三棱锥的体积最大值为,故C正确;
对于,当三棱锥的体积达到最大值时,
三棱锥外接球的球心为,
故球的半径为,则球的表面积为故D正确.
故选:.
由立体几何的线线平行,线面垂直判定定理,外接球的表面积公式逐项判断即可.
本题考查线线平行的判断,线线垂直的证明,三棱锥的体积的最值的求解,三棱锥的外接球问题,属中档题.
10.【答案】
【解析】解:由茎叶图中的数据,我们可得甲、乙甲,乙两地某月时的气温抽取的样本温度分别为:
甲:,,,,
乙:,,,,;
可得:甲地该月时的平均气温:,
乙地该月时的平均气温:,
故甲地该月时的平均气温低于乙地该月时的平均气温;
甲地该月时温度的方差为:
乙地该月时温度的方差为:,
故,
所以甲地该月时的气温的标准差大于乙地该月时的气温标准差.
故选:.
由已知的茎叶图,我们易分析出甲、乙甲,乙两地某月时的气温抽取的样本温度,进而求出两组数据的平均数、及方差可得答案
解:由茎叶图中的数据,我们可得甲、乙甲,乙两地某月时的气温抽取的样本温度分别为:
甲:,,,,
乙:,,,,;
可得:甲地该月时的平均气温:,
乙地该月时的平均气温:,
故甲地该月时的平均气温低于乙地该月时的平均气温;
甲地该月时温度的方差为:
乙地该月时温度的方差为:,
故,
所以甲地该月时的气温的标准差大于乙地该月时的气温标准差.
故选:.
11.【答案】
【解析】解:因为,所以,
则,即,所以,
当时,,
又满足上式,
所以,故A正确,B错误;
易知,因为,,
所以,当时,,
所以当时,,当时,,
所以数列不是递增数列,且当时,取得最小值,故C错误,D正确.
故选:.
由即可求得,及,从而判断选项A,;求出数列的通项公式,可得,从而可得当时取得最小值,即可判断选项C,.
本题主要考查数列递推式,考查数列的通项的求法,属于中档题.
12.【答案】
【解析】解:过点作垂线,垂足为,则,
三棱锥的体积为,则选项A错误;
当点与点重合时,此时直线与平面所成角正弦值的最大,且最大值为,则选项B正确;
由可知与点重合,又因为,易知与不垂直,
故B与不垂直,与平面不垂直,则选项C错误;
四边形的周长为,周长取得最小值即最小,
将平面与平面放在同一平面内,可知最小值为:,
截面四边形的周长取得最小值,则选项D正确;
故选:.
根据空间几何体中相关知识进行判断即可.
本题是对立体几何问题的综合考查,涉及了三棱锥的体积,线面角,线面垂直以及存在性问题等,考查逻辑推理能力以及运算求解能力,属于中档题.
13.【答案】
【解析】解:根据题意,先将位同学看成个排成一列的盒子,先从这个不同的盒子中选出个,并从左往右依次放入、、号球,
再从剩余的个盒子中选出个并从左往右依次放入、、号球,
最后将、、号球从左往右依次放入剩余的个盒子,
共有种不同的站法,
故答案为:.
根据题意,先将位同学看成个排成一列的盒子,在其中放入号个小球的问题,由分步计数原理计算可得答案.
本题考查排列组合的应用,注意将原问题转化,利用分步计数原理解决,属于基础题.
14.【答案】
【解析】解:圆:的圆心,半径,
直线:恒过定点,则,
设中点为,则点在以为直径的圆上,圆心到直线:距离为,
则,
则的面积为,
当,即时,取得最大值.
则面积的最大值为.
故答案为:.
先求得面积的表达式,再利用二次函数的性质即可求得面积的最大值.
本题考查了直线过定点问题以及直线与圆的位置关系,属于中档题.
15.【答案】
【解析】解:由题意可得,存在,使,即,
化简可得,令,其中,
则,令,可得,
当时,,则单调递减,
当时,,则单调递增,
所以,当时,有极小值,即最小值,
即,所以,
记,其中,
则,令,解得,
当时,,则函数单调递增,
当时,,则函数单调递减,
所以,当时,有极大值,即最大值,
所以,则,即实数的取值范围是
故答案为:
根据题意,分离参数,然后结合导数求最值,即可得到结果.
本题主要考查了利用导数求最值问题,解答本题的关键在于分离参数,然后利用导数求解最值,属于中档题.
16.【答案】
【解析】解:双曲线的一条渐近线方程为:,
点到双曲线的渐近线的距离是:.
故答案为:.
求出双曲线的渐近线方程,利用点到直线的距离公式求解即可.
本题考查双曲线的简单性质的应用,点到直线的距离公式的应用,是基础题.
17.【答案】解:由题意:,,
两式相减有:,
化简得:,
因为,所以.
又因为,所以,所以,
所以是首项为,公差为的等差数列,
所以.
不妨设的公比为,则有,且,
所以,
所以,所以,
所以.
令,
所以
,
则易得是一个单调递增数列,
因为,,
所以的最小值为.
【解析】本题主要考查了等差数列的通项公式求和公式,等比数列的通项公式求和公式.
由已知利用等差数列的通项公式,等比数列的通项公式即可求解;
利用分组求和法进行求解.
18.【答案】解:由题意可知,甲村中“绝对贫困户”有户,
甲、乙两村的绝对贫困户有户,可得出如下列联表:
甲村 乙村 总计
绝对贫困户
相对贫困户
总计
.
故没有的把握认为绝对贫困户数与村落有关.
贫困指标在的贫困户共有户,
“亟待帮助户”共有户,
依题意的可能值为,,,,
,
,
,
,
则的分布列为:
故.
【解析】甲村中“绝对贫困户”有户,甲、乙两村的绝对贫困户有户,由此能完成列联表,求出,从而没有的把握认为绝对贫困户数与村落有关.
贫困指标在的贫困户共有户,“亟待帮助户”共有户,依题意的可能值为,,,,分别求出相应的概率,由此能求出的分布列和数学期望.
本题考查独立检验的应用,考查离散型别的事同变量的分布列、数学期望的求法,考查频率分布直方图、排列组合等基础知识,考查运算求解能力,是中档题.
19.【答案】解:,的定义域为,
,
令,解得;令,解得,
所以函数在上单调递减,在上单调递增,
故有极小值,无极大值.
当时,,
令,,
,令,
当,即时,
此时,在上单调递增,
所以,满足题意;
当,即时,
令,解得;令,解得,
故函数在上单调递减,在上单调递增,
,
令,,,,
所以在上单调递减,
又,,,当时,,
所以在上存在唯一的零点,
于是,
综上所述,的取值范围为,其中,
又,故的最大值为.
证明:,的定义域为,
,
令,解得;令,解得,
故在上单调递减,在上单调递减,
又,所以,
题意转化为,,且时,,
等价于证明函数在上单调递减,
等价于证明对恒成立,
令,,
即证明对恒成立,
显然在上单调递减,
又,所以,
命题得证.
【解析】Ⅰ先求导得到函数的单调性,进而求的极值;
Ⅱ,构造新函数,,求出的取值范围,结合,可求的最大值;
Ⅲ先求出,把不等式转化为,进而命题等价于函数在上单调递减,再利用导数符号与函数单调性的关系可证明.
本题考查导数的应用,利用导数研究函数的单调性、极值、最值和零点,考查数学抽象和数学运算的核心素养,属于难题.
20.【答案】解:平面,,平面,,,,
以为正交基底建立空间直角坐标系,
则各点的坐标为,,,
,,,平面,,
平面,
是平面的一个法向量,.
,.
设平面的法向量为,
则,,
即,令,解得,.
是平面的一个法向量,
可得,,
由图可知,二面角为锐二面角,
二面角的余弦值为;
,设,
又,
则,
又,
,,
设,,
则,
,
当且仅当,即时,
即,的最大值为.
因为在上是减函数,此时直线与所成角取得最小值,
又,
.
【解析】本题考查向量法解决立体几何问题,建系并把问题转化为向量的夹角和模长是解决问题的关键,属于难题.
以为正交基底建立空间直角坐标系,由题意可得,,,
易得是平面的一个法向量,待定系数可求平面的法向量为坐标,由向量的夹角公式可得;
设,由夹角公式和二次函数的值域以及余弦函数的单调性可得.
21.【答案】解:Ⅰ设第年春季植树为亩,
由题意可知,常数,
所以为等差数列.
设植树年新建防护林计划全部完成,则,
化简得,,
所以,,
所以到年新建防护林计划全部完成;
Ⅱ设每年种植树木到年底的木材量为数列,
则,,
,,
则本材总量,
则,
所以,
,
解得,
所以到年底新建防护林的木材总量为立方米.
【解析】本题考查了数列在实际生活中的应用,涉及了等差数列求和公式、等比数列求和公式的应用,同时考查了错位相减法求和,对学生的理解能力和运算能力有一定的要求.
Ⅰ设第年春季植树为亩,得到为等差数列,利用等差数列的求和公式分析求解即可;
Ⅱ设每年种植树木到年底的木材量为数列,然后利用错位相减法求和即可得到答案.
22.【答案】解:Ⅰ因为椭圆经过点,所以,
又因为,则
由,得,
所以椭圆的标准方程为.
Ⅱ方法一:
因为以为直径的圆过坐标原点,所以.
若直线的斜率不存在,则为椭圆与轴交点,为椭圆与轴交点,
因此,,
则.
若直线的斜率存在且为,则为椭圆与轴交点,为椭圆与轴交点,
因此,,
则.
若直线的斜率存在且不为,
可设直线方程为,
则直线的方程为.
联立,得,
即,,
即,
同理,,
则.
方法二:
若直线的斜率存在时,设:,与椭圆方程联立得:,
有,
由题意,,设,,
所以,.
因为以为直径的圆过原点,
由,得 ,
即,整理得,,
而.
设为到的距离,则
所以,
而,
所以.
若直线的斜率不存在,则有,
不妨设,设,有,
代入椭圆方程得,,,
即,
综上.
【解析】本题考查的知识要点:椭圆的方程的求法和应用,直线和椭圆的位置关系的应用,一元二次方程根和系数关系式的应用,主要考查学生的运算能力和转换能力及思维能力,属于中档题.
Ⅰ首先利用椭圆的离心率和椭圆经过的点的坐标求出和的值,最后求出,进一步求出椭圆的方程.
Ⅱ利用分类讨论思想的应用假设直线的斜率不存在求出结果为定值,当直线的斜率存在时,建立直线和椭圆的方程组,进一步利用一元二次方程根和系数关系式的应用求出结果为定值.
第1页,共1页
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 复数,则( )
A. B. C. D.
2. 的展开式中常数项为( )
A. B. C. D.
3. 已知等差数列满足,,其前项和为,则使成立时最大值为( )
A. B. C. D.
4. 袋中装有个红球和个白球,不放回地一次摸出一个,在第一次摸出红球的条件下,第二次摸到红球的概率为( )
A. B. C. D.
5. 已知函数的图象关于直线对称,则函数的单调递增区间为( )
A. B. C. D.
6. 如图是梁思成研究广济寺三大士殿的手稿,它是该建筑中垂直于房梁的截面,其中是房梁与该截面的交点,,分别是两房檐与该截面的交点,该建筑关于房梁所在铅垂面垂直于水平面的面对称,测得柱子与之间的距离是为测量单位,柱子与之间的距离是如果把,视作线段,记,,是的四等分点,,,是的四等分点,若,则线段的长度为( )
A. B. C. D.
7. ,是椭圆上两点,线段的中点在直线上,则直线与轴的交点的纵坐标的取值范围是( )
A. B.
C. D.
8. 在概率论中,全概率公式指的是:设为样本空间,若事件,,,两两互斥,,则对任意的事件,有若甲盒中有个白球、个红球、个黑球,乙盒中有个白球、个红球、个黑球,现从甲盒中随机取出一个球放入乙盒,再从乙盒中随机取出一个球,若从甲盒中取出的球和从乙盒中取出的球颜色相同的概率大于等于,则的最大值为( )
A. B. C. D.
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
9. 如图,矩形中,、分别为、的中点,且,现将沿问上翻折,使点移到点,则在翻折过程中,下列结论正确的是( )
A. 存在点,使得
B. 存在点,使得
C. 三棱锥的体积最大值为
D. 当三棱锥的体积达到最大值时,三棱锥外接球表面积为
10. 为比较甲,乙两地某月时的气温,随机选取该月中的天,将这天中时的气温数据单位:制成如图所示的茎叶图,考虑以下结论中根据茎叶图能得到的统计结论的为( )
A. 甲地该月时的平均气温低于乙地该月时的平均气温
B. 甲地该月时的平均气温高于乙地该月时的平均气温
C. 甲地该月时的气温的标准差小于乙地该月时的气温的标准差
D. 甲地该月时的气温的标准差大于乙地该月时的气温的标准差
11. 已知数列的前项和为,且,,则( )
A. B.
C. 数列是递增数列 D. 数列的最小值为
12. 如图,已知在长方体中,,,,点为棱上的一个动点,平面与棱交于,则下列说法正确的是( )
A. 三棱锥的体积为
B. 直线与平面所成角正弦值的最大值为
C. 存在唯一的点,使得平面,且
D. 存在唯一的点,使截面四边形的周长取得最小值
三、填空题(本大题共4小题,共20.0分)
13. 现有学号分别为号、号、号、、号的位同学依次站成一排,老师请他们从号同学开始依次从如图所示的装有标号为至号球的三个圆柱形容器中随意选择一个有球的容器并取出最上面的一个球,再根据自己手中所拿球的号码,按照球号从小到大的顺序从左到右重新站成一排,则所有可能的不同站法有______ 种用数字作答.
14. 若直线:与圆:交于,两点,则面积的最大值为______ .
15. 已知为实数,函数,若存在,使,则的取值范围为______ .
16. 点到双曲线的渐近线的距离为______.
四、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
已知与都是正项数列,的前项和为,,且满足,等比数列满足,.
求数列,的通项公式;
记数列的前项和为,求满足不等式的自然数的最小值.
18. 本小题分
在贯彻中共中央、国务院关于精准扶贫政策的过程中,某单位在某市定点帮扶甲、乙两村各户贫困户.为了做到精准帮扶,工作组对这户村民的年收入情况、劳动能力情况.子女受教育情况、危旧房情况、患病情况等进行调查.并把调查结果转化为各户的贫困指标将指标按照,,,,分成五组,得到如图所示的频率分布直方图.规定若,则认定该户为“绝对贫困户”,否则认定该户为“相对贫困户”,且当时,认定该户为“低收入户”;当时,认定该户为“亟待帮助户“已知此次调查中甲村的“绝对贫困户”占甲村贫困户的.
完成下面的列联表,并判断是否有的把握认为绝对贫困户数与村落有关:
甲村 乙村 总计
绝对贫困户
相对贫困户
总计
某干部决定在这两村贫困指标处于的贫困户中,随机选取户进行帮扶,用表示所选户中“亟待帮助户”的户数,求的分布列和数学期望.
附:,其中.
19. 本小题分
已知函数.
Ⅰ求的极值;
Ⅱ已知,且对任意的恒成立,求的最大值;
Ⅲ设的零点为,当,,且时,证明:.
20. 本小题分
如图,平面,,分别是,中点,,.
求二面角的余弦值;
点是线段上的动点,当直线与所成的角最小时,求线段的长.
21. 本小题分
沿海某市为了进一步完善海防生态防护体系,林业部门计划在沿海新建防护林万亩,从年开始,每年春季在规划的区域内植树造林,第一年植树亩,以后每一年比上一年多植树亩,假设所植树木全部成活.
Ⅰ求到哪一年春季新建防护林计划全部完成;
Ⅱ若每亩新植树苗的木材量为立方米,且所植树木每一年从春季开始生长,到年底停止生长时木材量的年自然增长率为,到新建防护林计划全部完成的那一年底,新建防护林的木材总量为多少立方米参考数据:
22. 本小题分
已知椭圆的离心率为,且经过点,一条直线与椭圆交于,两点,以为直径的圆经过坐标原点.
Ⅰ求椭圆的标准方程;
Ⅱ求证:为定值.
答案和解析
1.【答案】
【解析】解:复数,
则,
故选:.
利用复数的运算法则、共轭复数的定义即可得出.
本题考查了复数的运算法则、共轭复数的定义,属于基础题.
2.【答案】
【解析】
【分析】
本题考查了二项式定理的应用,属于中档题.
由的通项公式,即可得解.
【解答】
解:由的通项公式,
当即时,,
当即时,,
的展开式中常数项.
故选:.
3.【答案】
【解析】解:等差数列的首项,,,
,.
于是,
.
使成立的最大正整数是.
故选:.
差数列的首项,,,可得,再利用求和公式及其性质即可得出..
本题考查了等差数列的通项公式求和公式及其性质,考查了推理能力与计算能力,属于中档题.
4.【答案】
【解析】解:袋中装有个红球和个白球,不放回地一次摸出一个,
第一次摸到红球,
第二次摸球时袋中有个红球和个白球,
第二次摸到红球的概率为.
故选:.
第一次摸到红球,第二次摸球时袋中有个红球和个白球,由此能求出第二次摸到红球的概率.
本题考查概率的求法,是中档题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.
5.【答案】
【解析】解:函数的图象关于直线对称,
,即,
即,
.
,.
由于为开口向下的抛物线,其对称轴为,定义域为,
它的递增区间为,
由复合函数的单调性知,
的单调递增区间为,
故选:.
函数的图象关于直线对称,可求得,利用复合函数的单调性解求得答案.
本题考查利用导数研究函数的单调性,突出考查复合函数的单调性的应用,考查推理与运算能力,属于中档题.
6.【答案】
【解析】解:根据题意作出示意图,如图所示,其中点与点重合,
该建筑关于房梁所在铅垂面垂直于水平面的面对称,
又,,是的四等分点,,,是的四等分点,
,,,,,
为直角三角形,四边形为矩形,
,且,,
又,,
,
,
.
故选:.
画出平面图形,数形结合,根据余弦定理,即可求解.
本题考查两点间距离的求解,余弦定理的应用,方程思想,化归转化思想,属中档题.
7.【答案】
【解析】解:由题意可知,直线的斜率必然存在,设直线的方程为,
则直线与轴的交点的纵坐标为,设点,,
将直线的方程与椭圆方程联立并化简得,,
化简得,即.
由韦达定理可得,所以,
将等式两边平方得,所以.
当且仅当时,等号成立,由于,解得或.
因此,直线与轴的交点的纵坐标的取值范围是.
故选:.
设直线的方程为,点,,联立直线与椭圆的方程,根据判别式与韦达定理求解的范围即可.
本题主要考查椭圆的性质,直线与椭圆的综合,考查运算求解能力,属于中档题.
8.【答案】
【解析】
【分析】
本题考查全概率公式,属于中档题.
分别求出两次取出的球都是白球的概率,两次取出的球都是红球的概率,两次取出的球都是黑球的概率,将他们加起来得,再解不等式,即可得到结果.
【解答】
解:两次取出的球都是白球的概率;
两次取出的球都是红球的概率;
两次取出的球都是黑球的概率;
两次取出的球的颜色相同的概率,
则,解得,
则的最大值为.
故选C.
9.【答案】
【解析】解:对于,,,因此,不平行,
即不存在点,使得故A错误;
对于,如图:
取的中点,连接,,,,当时,
因为,即则,
而,,平面,
又,分别为,的中点,
即,于是平面,而平面,
则,故B正确;
对于,在翻折过程中,令与平面所成角为,
则点到平面的距离 ,
又的面积为,
因此三棱锥的体积为:,
当且仅当时,即平面时取等号,
所以三棱锥的体积最大值为,故C正确;
对于,当三棱锥的体积达到最大值时,
三棱锥外接球的球心为,
故球的半径为,则球的表面积为故D正确.
故选:.
由立体几何的线线平行,线面垂直判定定理,外接球的表面积公式逐项判断即可.
本题考查线线平行的判断,线线垂直的证明,三棱锥的体积的最值的求解,三棱锥的外接球问题,属中档题.
10.【答案】
【解析】解:由茎叶图中的数据,我们可得甲、乙甲,乙两地某月时的气温抽取的样本温度分别为:
甲:,,,,
乙:,,,,;
可得:甲地该月时的平均气温:,
乙地该月时的平均气温:,
故甲地该月时的平均气温低于乙地该月时的平均气温;
甲地该月时温度的方差为:
乙地该月时温度的方差为:,
故,
所以甲地该月时的气温的标准差大于乙地该月时的气温标准差.
故选:.
由已知的茎叶图,我们易分析出甲、乙甲,乙两地某月时的气温抽取的样本温度,进而求出两组数据的平均数、及方差可得答案
解:由茎叶图中的数据,我们可得甲、乙甲,乙两地某月时的气温抽取的样本温度分别为:
甲:,,,,
乙:,,,,;
可得:甲地该月时的平均气温:,
乙地该月时的平均气温:,
故甲地该月时的平均气温低于乙地该月时的平均气温;
甲地该月时温度的方差为:
乙地该月时温度的方差为:,
故,
所以甲地该月时的气温的标准差大于乙地该月时的气温标准差.
故选:.
11.【答案】
【解析】解:因为,所以,
则,即,所以,
当时,,
又满足上式,
所以,故A正确,B错误;
易知,因为,,
所以,当时,,
所以当时,,当时,,
所以数列不是递增数列,且当时,取得最小值,故C错误,D正确.
故选:.
由即可求得,及,从而判断选项A,;求出数列的通项公式,可得,从而可得当时取得最小值,即可判断选项C,.
本题主要考查数列递推式,考查数列的通项的求法,属于中档题.
12.【答案】
【解析】解:过点作垂线,垂足为,则,
三棱锥的体积为,则选项A错误;
当点与点重合时,此时直线与平面所成角正弦值的最大,且最大值为,则选项B正确;
由可知与点重合,又因为,易知与不垂直,
故B与不垂直,与平面不垂直,则选项C错误;
四边形的周长为,周长取得最小值即最小,
将平面与平面放在同一平面内,可知最小值为:,
截面四边形的周长取得最小值,则选项D正确;
故选:.
根据空间几何体中相关知识进行判断即可.
本题是对立体几何问题的综合考查,涉及了三棱锥的体积,线面角,线面垂直以及存在性问题等,考查逻辑推理能力以及运算求解能力,属于中档题.
13.【答案】
【解析】解:根据题意,先将位同学看成个排成一列的盒子,先从这个不同的盒子中选出个,并从左往右依次放入、、号球,
再从剩余的个盒子中选出个并从左往右依次放入、、号球,
最后将、、号球从左往右依次放入剩余的个盒子,
共有种不同的站法,
故答案为:.
根据题意,先将位同学看成个排成一列的盒子,在其中放入号个小球的问题,由分步计数原理计算可得答案.
本题考查排列组合的应用,注意将原问题转化,利用分步计数原理解决,属于基础题.
14.【答案】
【解析】解:圆:的圆心,半径,
直线:恒过定点,则,
设中点为,则点在以为直径的圆上,圆心到直线:距离为,
则,
则的面积为,
当,即时,取得最大值.
则面积的最大值为.
故答案为:.
先求得面积的表达式,再利用二次函数的性质即可求得面积的最大值.
本题考查了直线过定点问题以及直线与圆的位置关系,属于中档题.
15.【答案】
【解析】解:由题意可得,存在,使,即,
化简可得,令,其中,
则,令,可得,
当时,,则单调递减,
当时,,则单调递增,
所以,当时,有极小值,即最小值,
即,所以,
记,其中,
则,令,解得,
当时,,则函数单调递增,
当时,,则函数单调递减,
所以,当时,有极大值,即最大值,
所以,则,即实数的取值范围是
故答案为:
根据题意,分离参数,然后结合导数求最值,即可得到结果.
本题主要考查了利用导数求最值问题,解答本题的关键在于分离参数,然后利用导数求解最值,属于中档题.
16.【答案】
【解析】解:双曲线的一条渐近线方程为:,
点到双曲线的渐近线的距离是:.
故答案为:.
求出双曲线的渐近线方程,利用点到直线的距离公式求解即可.
本题考查双曲线的简单性质的应用,点到直线的距离公式的应用,是基础题.
17.【答案】解:由题意:,,
两式相减有:,
化简得:,
因为,所以.
又因为,所以,所以,
所以是首项为,公差为的等差数列,
所以.
不妨设的公比为,则有,且,
所以,
所以,所以,
所以.
令,
所以
,
则易得是一个单调递增数列,
因为,,
所以的最小值为.
【解析】本题主要考查了等差数列的通项公式求和公式,等比数列的通项公式求和公式.
由已知利用等差数列的通项公式,等比数列的通项公式即可求解;
利用分组求和法进行求解.
18.【答案】解:由题意可知,甲村中“绝对贫困户”有户,
甲、乙两村的绝对贫困户有户,可得出如下列联表:
甲村 乙村 总计
绝对贫困户
相对贫困户
总计
.
故没有的把握认为绝对贫困户数与村落有关.
贫困指标在的贫困户共有户,
“亟待帮助户”共有户,
依题意的可能值为,,,,
,
,
,
,
则的分布列为:
故.
【解析】甲村中“绝对贫困户”有户,甲、乙两村的绝对贫困户有户,由此能完成列联表,求出,从而没有的把握认为绝对贫困户数与村落有关.
贫困指标在的贫困户共有户,“亟待帮助户”共有户,依题意的可能值为,,,,分别求出相应的概率,由此能求出的分布列和数学期望.
本题考查独立检验的应用,考查离散型别的事同变量的分布列、数学期望的求法,考查频率分布直方图、排列组合等基础知识,考查运算求解能力,是中档题.
19.【答案】解:,的定义域为,
,
令,解得;令,解得,
所以函数在上单调递减,在上单调递增,
故有极小值,无极大值.
当时,,
令,,
,令,
当,即时,
此时,在上单调递增,
所以,满足题意;
当,即时,
令,解得;令,解得,
故函数在上单调递减,在上单调递增,
,
令,,,,
所以在上单调递减,
又,,,当时,,
所以在上存在唯一的零点,
于是,
综上所述,的取值范围为,其中,
又,故的最大值为.
证明:,的定义域为,
,
令,解得;令,解得,
故在上单调递减,在上单调递减,
又,所以,
题意转化为,,且时,,
等价于证明函数在上单调递减,
等价于证明对恒成立,
令,,
即证明对恒成立,
显然在上单调递减,
又,所以,
命题得证.
【解析】Ⅰ先求导得到函数的单调性,进而求的极值;
Ⅱ,构造新函数,,求出的取值范围,结合,可求的最大值;
Ⅲ先求出,把不等式转化为,进而命题等价于函数在上单调递减,再利用导数符号与函数单调性的关系可证明.
本题考查导数的应用,利用导数研究函数的单调性、极值、最值和零点,考查数学抽象和数学运算的核心素养,属于难题.
20.【答案】解:平面,,平面,,,,
以为正交基底建立空间直角坐标系,
则各点的坐标为,,,
,,,平面,,
平面,
是平面的一个法向量,.
,.
设平面的法向量为,
则,,
即,令,解得,.
是平面的一个法向量,
可得,,
由图可知,二面角为锐二面角,
二面角的余弦值为;
,设,
又,
则,
又,
,,
设,,
则,
,
当且仅当,即时,
即,的最大值为.
因为在上是减函数,此时直线与所成角取得最小值,
又,
.
【解析】本题考查向量法解决立体几何问题,建系并把问题转化为向量的夹角和模长是解决问题的关键,属于难题.
以为正交基底建立空间直角坐标系,由题意可得,,,
易得是平面的一个法向量,待定系数可求平面的法向量为坐标,由向量的夹角公式可得;
设,由夹角公式和二次函数的值域以及余弦函数的单调性可得.
21.【答案】解:Ⅰ设第年春季植树为亩,
由题意可知,常数,
所以为等差数列.
设植树年新建防护林计划全部完成,则,
化简得,,
所以,,
所以到年新建防护林计划全部完成;
Ⅱ设每年种植树木到年底的木材量为数列,
则,,
,,
则本材总量,
则,
所以,
,
解得,
所以到年底新建防护林的木材总量为立方米.
【解析】本题考查了数列在实际生活中的应用,涉及了等差数列求和公式、等比数列求和公式的应用,同时考查了错位相减法求和,对学生的理解能力和运算能力有一定的要求.
Ⅰ设第年春季植树为亩,得到为等差数列,利用等差数列的求和公式分析求解即可;
Ⅱ设每年种植树木到年底的木材量为数列,然后利用错位相减法求和即可得到答案.
22.【答案】解:Ⅰ因为椭圆经过点,所以,
又因为,则
由,得,
所以椭圆的标准方程为.
Ⅱ方法一:
因为以为直径的圆过坐标原点,所以.
若直线的斜率不存在,则为椭圆与轴交点,为椭圆与轴交点,
因此,,
则.
若直线的斜率存在且为,则为椭圆与轴交点,为椭圆与轴交点,
因此,,
则.
若直线的斜率存在且不为,
可设直线方程为,
则直线的方程为.
联立,得,
即,,
即,
同理,,
则.
方法二:
若直线的斜率存在时,设:,与椭圆方程联立得:,
有,
由题意,,设,,
所以,.
因为以为直径的圆过原点,
由,得 ,
即,整理得,,
而.
设为到的距离,则
所以,
而,
所以.
若直线的斜率不存在,则有,
不妨设,设,有,
代入椭圆方程得,,,
即,
综上.
【解析】本题考查的知识要点:椭圆的方程的求法和应用,直线和椭圆的位置关系的应用,一元二次方程根和系数关系式的应用,主要考查学生的运算能力和转换能力及思维能力,属于中档题.
Ⅰ首先利用椭圆的离心率和椭圆经过的点的坐标求出和的值,最后求出,进一步求出椭圆的方程.
Ⅱ利用分类讨论思想的应用假设直线的斜率不存在求出结果为定值,当直线的斜率存在时,建立直线和椭圆的方程组,进一步利用一元二次方程根和系数关系式的应用求出结果为定值.
第1页,共1页
同课章节目录
