湖南省衡阳市重点中学2023-2024学年高一上学期入学分班考试数学模拟试卷(含解析)
文档属性
| 名称 | 湖南省衡阳市重点中学2023-2024学年高一上学期入学分班考试数学模拟试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-11 18:10:36 | ||
图片预览




文档简介
2023-2024学年度新高一入学分班考试
数学模拟卷
一.选择题(共12小题,满分36分,每小题3分)
1.(3分)下列计算正确的是( )
A.(a﹣b)2=a2﹣b2 B.(﹣2a2)3=8a4
C.a3÷a2=a D.2a2+a2=3a4
2.(3分)陕西历史博物馆是中国第一座大型现代化国家级博物馆,2021年春节期间累计接待游客约37200人次,数据37200用科学记数法可表示为( )
A.372×102 B.3.72×103 C.3.72×104 D.0.372×105
3.(3分)下列计算正确的是( )
A.a+a2=a3 B.a6÷a3=a3
C.(﹣a2b)3=a6b3 D.(a+2)2=a2+4
4.(3分)化简分式后得( )
A. B. C. D.
5.(3分)已知二元一次方程组,则(x+y)(x﹣y)的值是( )
A.15 B.﹣5 C.5 D.﹣15
6.(3分)已知:关于x的一元二次方程x2﹣(R+r)xd2=0无实数根,其中R,r分别是⊙O1,⊙O2的半径,d为此两圆的圆心距,则⊙O1,⊙O2的位置关系为( )
A.外离 B.相切 C.相交 D.内含
7.(3分)如图所示,在梯形ABCD中,AB∥CD,∠ABC=α,∠BAD=β,则AD:BC等于( )
A. B. C. D.
8.(3分)如图,已知点O是等边△ABC三条高的交点,现将△AOB绕点O至少要旋转几度后与△BOC重合( )
A.60° B.120° C.240° D.360°
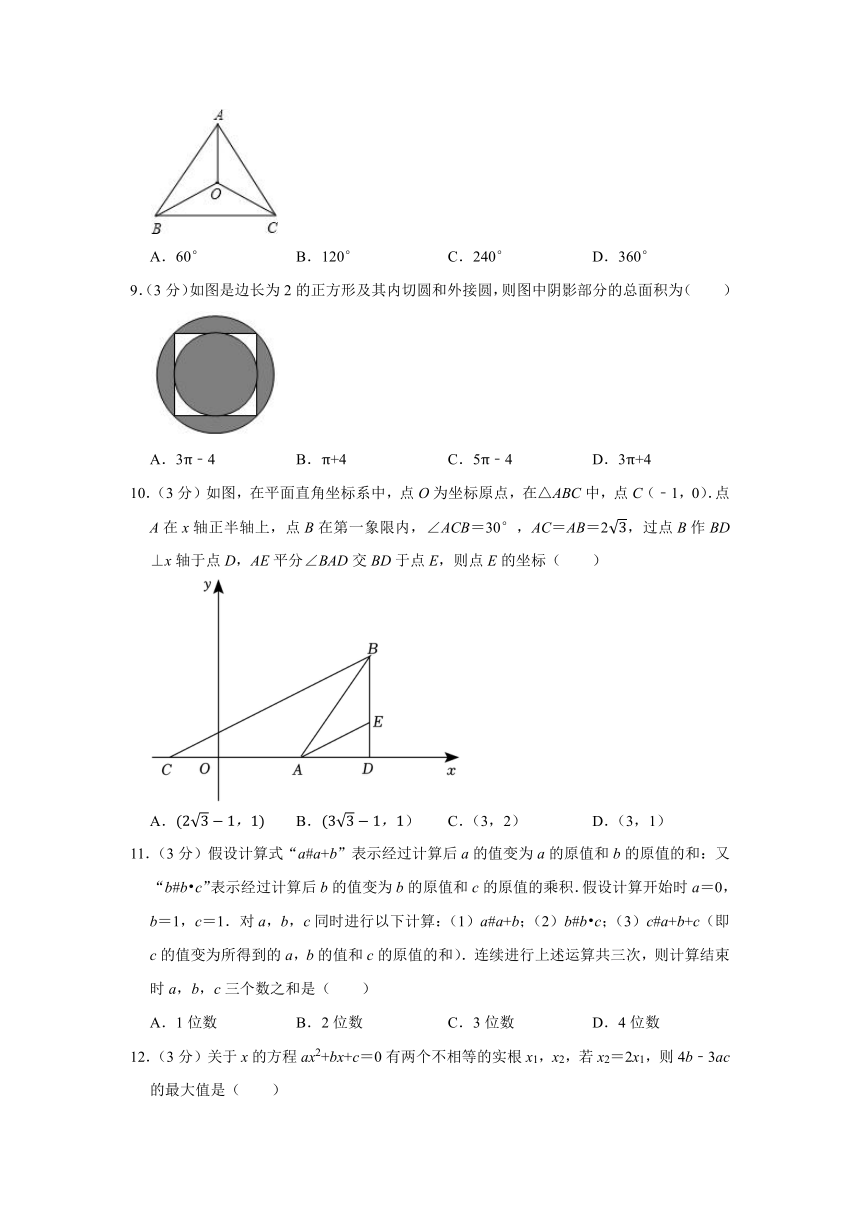
9.(3分)如图是边长为2的正方形及其内切圆和外接圆,则图中阴影部分的总面积为( )
A.3π﹣4 B.π+4 C.5π﹣4 D.3π+4
10.(3分)如图,在平面直角坐标系中,点O为坐标原点,在△ABC中,点C(﹣1,0).点A在x轴正半轴上,点B在第一象限内,∠ACB=30°,AC=AB=2,过点B作BD⊥x轴于点D,AE平分∠BAD交BD于点E,则点E的坐标( )
A. B.) C.(3,2) D.(3,1)
11.(3分)假设计算式“a#a+b”表示经过计算后a的值变为a的原值和b的原值的和:又“b#b c”表示经过计算后b的值变为b的原值和c的原值的乘积.假设计算开始时a=0,b=1,c=1.对a,b,c同时进行以下计算:(1)a#a+b;(2)b#b c;(3)c#a+b+c(即c的值变为所得到的a,b的值和c的原值的和).连续进行上述运算共三次,则计算结束时a,b,c三个数之和是( )
A.1位数 B.2位数 C.3位数 D.4位数
12.(3分)关于x的方程ax2+bx+c=0有两个不相等的实根x1,x2,若x2=2x1,则4b﹣3ac的最大值是( )
A.1 B.2 C.4 D.6
二.填空题(共6小题,满分15分)
13.(3分)如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=8,tan∠ABD,则线段AB的长为 .
14.(3分)关于x的方程()2=2,方程的所有的所有实根的和为 .
15.(3分)已知实数a,b满足a2+2a=b+2,b2+2b=a+2,则代数式的值等于 .
16.阅读材料:如果两个正数a、b,即a>0,b>0,则有下面的不等式,当且仅当a=b时取到等号.我们把叫做正数a、b算术平均数,把叫做正数a、b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具.根据上述材料,若,则y最小值为 .
17.(3分)若t为实数,x2﹣4x+t﹣2=0的两个非负实数根为a,b,则代数式(a2﹣1)(b2﹣1)的最小值
18.(3分)已知一次函数m与二次函数,若满足y1>0且y2<0时的自变量x的取值范围内有且只有一个整数,则m的取值范围是 .
三.解答题(共8小题,满分66分)
19.(6分)【阅读材料】:善于思考的小明在解方程组时,采用了一种“整体代换”的解法:解:将方程(2)变形:4x+10y+y=5,即2(2x+5y)+y=5(3),把方程(1)代入(3)得:2×3+y=5,所以y=﹣1,将y=﹣1代入(1)得x=4,所以原方程组的解为.
【解决问题】:
(1)模仿小明的“整体代换”法解方程组;
(2)已知x,y满足方程组,求x2+4y2的值.
20.(8分)2022年的冬天,越来越多的游客选择到山西九龙山滑雪场来放松一下自己,体验一下蓝蓝的天空,皑皑白雪的浪漫,重温一下儿时的激情和与大自然抗争的成就感,更能领略一下冬天滑雪的魅力.图1,图2分别是一名滑雪爱好者在滑雪过程中某一时刻的实景图与示意图,此时运动员的小腿ED与斜坡AB垂直,大腿EF与斜坡AB平行,G为头部,且G,E,D三点共线.若滑雪杖EM长为1m,EF=0.4m,∠EMD=30°,∠GFE=62°,求此时滑雪爱好者头部G到斜坡AB的距离.(精确到0.1m)(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
21.(8分)青岛方特梦幻王国位于美丽的山东省青岛市红岛海滨,由深圳华强集团投资兴建.火流星是其经典项目之一.如图所示,F→E→G为火流星过山车的一部分轨道,它可以看成一段抛物线.其中OE米,OF米(轨道厚度忽略不计).
(1)求抛物线F→E→G的函数关系式;
(2)在轨道距离地面5米处有两个位置P和G,当过山车运动到G处时,平行于地面向前运动了米至K点,又进入下坡段K→H(K接口处轨道忽略不计).已知轨道抛物线K→H→Q的形状与抛物线P→E→G完全相同,在G到Q的运动过程中,求OH的距离;
(3)现需要在轨道下坡段F→E进行一种安全加固,建造某种材料的水平和竖直支架AM、CM、BN、DN,且要求OA=AB.已知这种材料的价格是80000元/米,如何设计支架,会使造价最低?最低造价为多少元?
22.(8分)解方程:x﹣2.
23.(8分)如图,AB是⊙O的直径,C是⊙O上一点,D是的中点,E为OD延长线上一点,且∠CAE=2∠C,AC与BD交于点H,与OE交于点F.
(1)求证:AE是⊙O的切线;
(2)若⊙O的半径10,,求线段DH的长.
24.(8分)二次函数y=x2+bx+c的图象与x轴交于点A(x1,0),B(x2,0)且x1≠x2.
(1)当x1=2,且b+c=﹣6时,
①求b,c的值;
②当t≤x≤t+2时,二次函数y=x2+bx+c的最小值为2t,求t的值;
(2)若x1=3x2,求证:.
25.(10分)(1)【探究发现】如图1,已知点O是正方形ABCD对角线的交点,点E是CB延长线上一点,作OF⊥OE交BA延长线于F点.小明探究发现,△EOF是等腰直角三角形.请证明这个结论.
(2)【模型应用】如图2,在(1)的结论下,延长DB、FE交于点P,若BC=6,BE=2,求BP的长.
(3)【拓展提升】如图3,若点G是正方形ABCD对角线BD上一点,DG=2BG,BC=6,点E在CB的延长线上运动时,连接EG,作FG⊥EG交直线AB于F点,设BE=x,记△EGF与正方形ABCD的重合面积为S,请直接写出S关于x的关系式.
26.(10分)已知点M(a,a+2)(a>0)在反比例函数的图象上,点H(0,1)在y轴上,连接MH,如图1,将MH绕着H点顺时针旋转90°至点M',点M'正好落在x轴上.
(1)求k的值和点M'的坐标;
(2)若点P在反比例函数图象上,连接HP并延长至点E,使得PE=PH,连接EM',PM',
①如图2,连接MP并延长交x轴于点Q,当PM′⊥x轴时,试说明EM′平分∠PM′Q;
②如图3,连接MM′交HE于点Q,将△MHM'沿着MM'翻折,记点H的对应点为H',若点H'恰好落在线段PE上,求△M′H′E与△PM′Q面积之比.
2023-2024学年度新高一入学分班考试
数学模拟卷
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.(3分)下列计算正确的是( )
A.(a﹣b)2=a2﹣b2 B.(﹣2a2)3=8a4
C.a3÷a2=a D.2a2+a2=3a4
【考点】完全平方公式;合并同类项;幂的乘方与积的乘方;同底数幂的除法.
【分析】各式计算得到结果,即可作出判断.
【解答】解:A、原式=a2﹣2ab+b2,不符合题意;
B、原式=﹣8a6,不符合题意;
C、原式=a,符合题意;
D、原式=3a2,不符合题意.
故选:C.
2.(3分)陕西历史博物馆是中国第一座大型现代化国家级博物馆,2021年春节期间累计接待游客约37200人次,数据37200用科学记数法可表示为( )
A.372×102 B.3.72×103 C.3.72×104 D.0.372×105
【考点】科学记数法—表示较大的数.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
【解答】解:37200=3.72×104,
故选:C.
3.(3分)下列计算正确的是( )
A.a+a2=a3 B.a6÷a3=a3
C.(﹣a2b)3=a6b3 D.(a+2)2=a2+4
【考点】完全平方公式;合并同类项;幂的乘方与积的乘方;同底数幂的除法.
【分析】根据合并同类项法则,同底数幂的除法的运算法则,幂的乘方与积的乘方的运算法则,完全平方公式解答即可.
【解答】解:A、a与a2不是同类项,不能合并,原计算错误,故此选项不符合题意;
B、a6÷a3=a3,原计算正确,故此选项符合题意;
C、(﹣a2b)3=﹣a6b3,原计算错误,故此选项不符合题意;
D、(a+2)2=a2+4a+4,原计算错误,故此选项不符合题意.
故选:B.
4.(3分)化简分式后得( )
A. B. C. D.
【考点】约分.
【分析】先把分子和分母因式分解,再约分即可得出答案.
【解答】解:原式
.
故选:B.
5.(3分)已知二元一次方程组,则(x+y)(x﹣y)的值是( )
A.15 B.﹣5 C.5 D.﹣15
【考点】二元一次方程组的解;解二元一次方程组.
【分析】利用①﹣②可求出(x﹣y)的值,利用(①+②)÷3可求出(x+y)的值,从而可得答案.
【解答】解:,
①+②得:3x+3y=15,
∴x+y=5,
①﹣②得:x﹣y=﹣1,
∴(x+y)(x﹣y)=5×(﹣1)=﹣5,
故选:B.
6.(3分)已知:关于x的一元二次方程x2﹣(R+r)xd2=0无实数根,其中R,r分别是⊙O1,⊙O2的半径,d为此两圆的圆心距,则⊙O1,⊙O2的位置关系为( )
A.外离 B.相切 C.相交 D.内含
【考点】圆与圆的位置关系;根的判别式.
【分析】解答本题,先要根据题意得出根的判别式,然后再针对两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系,得出具体位置关系.
【解答】解:根据题意,方程无实数根,可得(R+r)2﹣d2<0,
则:(R+r+d)(R+r﹣d)<0,
因为R+r+d>0,所以R+r﹣d<0,
即:d>R+r,
那么,两圆外离.
故选:A.
7.(3分)如图所示,在梯形ABCD中,AB∥CD,∠ABC=α,∠BAD=β,则AD:BC等于( )
A. B. C. D.
【考点】解直角三角形;梯形.
【分析】分别过点D和点C作DE⊥AB交AB于点E,CF⊥AB交AB于点F,根据sinα,sinβ,将两者相比即可求出结果.
【解答】解:过点D和点C作DE⊥AB交AB于点E,CF⊥AB交AB于点F.
∵AB∥CD,
∴DE=CF.
在Rt△ADE中,sinβ;
在Rt△BCF中,sinα.
故.
故选:B.
8.(3分)如图,已知点O是等边△ABC三条高的交点,现将△AOB绕点O至少要旋转几度后与△BOC重合( )
A.60° B.120° C.240° D.360°
【考点】旋转的性质;等边三角形的性质.
【分析】先根据等边三角形的性质得出∠AOB=∠AOC=∠BOC=120°,再根据旋转的性质得出△AOB绕点O旋转后与△BOC重合至少要旋转的度数.
【解答】解:∵点O是等边△ABC三条高的交点,
∴∠AOB=∠AOC=∠BOC=120°,
∴由旋转的性质得出△AOB绕点O逆时针至少旋转120度后与△BOC重合.
故选:B.
9.(3分)如图是边长为2的正方形及其内切圆和外接圆,则图中阴影部分的总面积为( )
A.3π﹣4 B.π+4 C.5π﹣4 D.3π+4
【考点】正多边形和圆;扇形面积的计算;正方形的性质;三角形的内切圆与内心.
【分析】阴影部分的面积=大圆面积减去正方形面积+小圆面积.
【解答】解:阴影部分的面积=大圆面积减去正方形面积+小圆面积=π ()2﹣4+π 12=3π﹣4,
故选:A.
10.(3分)如图,在平面直角坐标系中,点O为坐标原点,在△ABC中,点C(﹣1,0).点A在x轴正半轴上,点B在第一象限内,∠ACB=30°,AC=AB=2,过点B作BD⊥x轴于点D,AE平分∠BAD交BD于点E,则点E的坐标( )
A. B.) C.(3,2) D.(3,1)
【考点】解直角三角形;坐标与图形性质.
【分析】由AB=AC可得∠ABC=∠ACB,则可求得∠BAD=60°,利用余弦可求得AD的长度,再由角平分线的定义可得∠EAD=30°,利用正切即可求DE的长度,从而可点E的坐标.
【解答】解:∵AC=AB=2,∠ACB=30°,
∴∠ABC=∠ACB=30°,
∴∠BAD=∠ABC+∠ACB=60°,
∵BD⊥x轴于点D,
∴cos∠BAD,
∴cos60°,
解得:AD,
∵AE平分∠BAD,
∴∠EAD=30°,
∴tan∠EAD,
即tan30°,
解得:DE=1,
∵点C(﹣1,0),
∴AO=AC﹣1=21,
∴OD=AO+AD=31,
∴点E的坐标为:(31,1).
故选:B.
11.(3分)假设计算式“a#a+b”表示经过计算后a的值变为a的原值和b的原值的和:又“b#b c”表示经过计算后b的值变为b的原值和c的原值的乘积.假设计算开始时a=0,b=1,c=1.对a,b,c同时进行以下计算:(1)a#a+b;(2)b#b c;(3)c#a+b+c(即c的值变为所得到的a,b的值和c的原值的和).连续进行上述运算共三次,则计算结束时a,b,c三个数之和是( )
A.1位数 B.2位数 C.3位数 D.4位数
【考点】规律型:数字的变化类.
【分析】读懂上述运算,理解新运算的规则,按照新规则对a、b、c同时进行连续三次运算,最后求和确定答案.
【解答】解:对a、b、c同时进行连续三次运算后的结果如下:
运算次数 1 2 3
a 1 2 5
b 1 3 24
c 3 8 37
经过三次运算后,a+b+c=5+24+37=66,它是一个两位数.
故选:B.
12.(3分)关于x的方程ax2+bx+c=0有两个不相等的实根x1,x2,若x2=2x1,则4b﹣3ac的最大值是( )
A.1 B.2 C.4 D.6
【考点】根与系数的关系;根的判别式.
【分析】根据根与系数的关系得出x1+x2,x1x2,由x2=2x1得出3x1,即x1,可解出x2,由两根之积可得acb2,代入代数式即可得到4b﹣3ac(b﹣3)2+6,从而求得4b﹣3ac的最大值是6.
【解答】解:∵关于x的方程ax2+bx+c=0有两个不相等的实根x1、x2,
∴x1+x2,x1x2,
∵x2=2x1,
∴3x1,即x1,
∴x2,
∴,
∴acb2,
∴4b﹣3ac=4b﹣3b2=4bb2(b﹣3)2+6,
∵0,
∴4b﹣3ac的最大值是6,
故选:D.
二.填空题(共6小题,满分15分)
13.(3分)如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=8,tan∠ABD,则线段AB的长为 5 .
【考点】菱形的性质;解直角三角形.
【分析】由菱形的性质得BO=ODBD=4,AC⊥BD,再由锐角三角函数定义求出OAOB=3,然后由勾股定理求出AB的长即可.
【解答】解:∵四边形ABCD为菱形,BD=8,
∴BO=ODBD=4,AC⊥BD,
∴∠AOB=90°,
∵tan∠ABD,
∴OAOB=3,
在Rt△ABC中,AO=3,OB=4,
∴AB5,
故答案为:5.
14.(3分)关于x的方程()2=2,方程的所有的所有实根的和为 .
【考点】换元法解分式方程.
【分析】可根据方程特点设y,则原方程可化为y+y2=2.解一元二次方程求y,再求x.
【解答】解:设y,则原方程可化为y+y2=2.解得y1=1,y2=﹣2,
当y1=1时,1,无解;
当y2=﹣2时,2,x,经检验x,是原方程的解.
故答案为.
15.(3分)已知实数a,b满足a2+2a=b+2,b2+2b=a+2,则代数式的值等于 2或7 .
【考点】根与系数的关系;分式的化简求值.
【分析】分两种情况:(1)当a=b时;(2)当a≠b时,联立方程组,运用加减消元法并结合完全平方公式,求得a2+b2和ab的值,然后将原式通分化简,代入求解.
【解答】解:(1)当a=b时,1+1=2;
(2)当a≠b时,联立方程组,
将①+②得:a2+b2+2a+2b=b+a+4,
整理得:a2+b2+a+b=4③,
将①﹣②得:a2﹣b2+2a﹣2b=b﹣a,
整理得:a2﹣b2+3a﹣3b=0,
(a+b)(a﹣b)+3(a﹣b)=0,
(a﹣b)(a+b+3)=0,
又∵a≠b,
∴a+b+3=0,即a+b=﹣3④,
将④代入③,得a2+b2﹣3=4,即a2+b2=7,
又∵(a+b)2=a2+2ab+b2=9,
∴ab=1,
∴7.
综上所述,代数式的值等于2或7.
故答案为:2或7.
16.阅读材料:如果两个正数a、b,即a>0,b>0,则有下面的不等式,当且仅当a=b时取到等号.我们把叫做正数a、b算术平均数,把叫做正数a、b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具.根据上述材料,若,则y最小值为 6 .
【考点】因式分解的应用;不等式的定义.
【分析】依据题意,读懂题目然后由公式可以得a+b≥2,从而y≥26,进而可以得解.
【解答】解:由题意,∵,
∴a+b≥2.
∵x>0,
∴3x>0,0,
∴y=3x226.
故答案为:6.
17.(3分)若t为实数,x2﹣4x+t﹣2=0的两个非负实数根为a,b,则代数式(a2﹣1)(b2﹣1)的最小值 ﹣15
【考点】根与系数的关系.
【分析】先根据根与系数的关系可得a+b=4,ab=t﹣2,将所求代数式化简代入可得结论.
【解答】解:∵x2﹣4x+t﹣2=0的两个非负实数根为a,b,
∴a+b=4,ab=t﹣2,Δ=16﹣4(t﹣2)≥0.
则,解得:2≤t≤6,
∴a2+b2=(a+b)2﹣2ab=42﹣2(t﹣2)=﹣2t+20,
∴(a2﹣1)(b2﹣1)=a2b2﹣(a2+b2)+1=(t﹣2)2+2t﹣20+1=t2﹣2t﹣15=(t﹣1)2﹣16,
∵2≤t≤6,
∴当t=2时,代数式(a2﹣1)(b2﹣1)有最小值,
∴代数式(a2﹣1)(b2﹣1)的最小值是1﹣16=﹣15,
故答案为:﹣15.
18.(3分)已知一次函数m与二次函数,若满足y1>0且y2<0时的自变量x的取值范围内有且只有一个整数,则m的取值范围是 m≤﹣1 .
【考点】抛物线与x轴的交点;一次函数的性质;二次函数的性质.
【分析】令y2=0可求出二次函数图象与x轴的交点坐标,进而可得出满足y2<0时自变量x的取值范围,结合满足y1>0且y2<0时的自变量x的取值范围内有且只有一个整数,即可得出关于m的一元一次不等式组,解之即可得出结论.
【解答】解:令y2=0,即x2﹣5x+4=0,
解得:x1=1,x2=4,
∴满足y2<0时自变量x的取值范围为1<x<4.
∵满足y1>0且y2<0时的自变量x的取值范围内有且只有一个整数,
∴,
∴m≤﹣1.
故答案为:m≤﹣1.
三.解答题(共8小题,满分66分)
19.(6分)【阅读材料】:善于思考的小明在解方程组时,采用了一种“整体代换”的解法:解:将方程(2)变形:4x+10y+y=5,即2(2x+5y)+y=5(3),把方程(1)代入(3)得:2×3+y=5,所以y=﹣1,将y=﹣1代入(1)得x=4,所以原方程组的解为.
【解决问题】:
(1)模仿小明的“整体代换”法解方程组;
(2)已知x,y满足方程组,求x2+4y2的值.
【考点】二元一次方程组的解;解二元一次方程组.
【分析】(1)将方程②化为3x+2(3x﹣2y)=19,再将方程①代入可求出x的值,进而求出方程组的解即可;
(2)将方程②×2,再与方程①相加后化简即可.
【解答】解:(1),
由②可得,3x+2(3x﹣2y)=19③,
将①代入③得,3x+10=19,
解得x=3,
把x=3代入①得,9﹣2y=5,
解得,y=2,
所以原方程组的解为;
(2),
②×2得,2x2+2xy+8y2=50③,
①+③得,5x2+20y2=100,
所以x2+4y2=20.
20.(8分)2022年的冬天,越来越多的游客选择到山西九龙山滑雪场来放松一下自己,体验一下蓝蓝的天空,皑皑白雪的浪漫,重温一下儿时的激情和与大自然抗争的成就感,更能领略一下冬天滑雪的魅力.图1,图2分别是一名滑雪爱好者在滑雪过程中某一时刻的实景图与示意图,此时运动员的小腿ED与斜坡AB垂直,大腿EF与斜坡AB平行,G为头部,且G,E,D三点共线.若滑雪杖EM长为1m,EF=0.4m,∠EMD=30°,∠GFE=62°,求此时滑雪爱好者头部G到斜坡AB的距离.(精确到0.1m)(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
【考点】解直角三角形的应用﹣坡度坡角问题.
【分析】连接GE,则GE⊥EF,GD=GE+ED,解直角△GEF,求出GE=EF tan62°≈0.752m,解直角△EDM,求出,代入GD=GE+ED,计算即可.
【解答】解:如图,连接GE′,
∵DE⊥AB且EF∥AB,
∴EF⊥GD,
则GE⊥EF,GD=GE+ED,
在直角△GEF中,
∵∠GEF=90°,∠GFE=62°,EF=0.4m,
∴GE=EF tan62°≈0.752m,
在直角△EDM中,
∵∠EDM=90°,∠EMD=30°,EM=1m,
∴,
∴GD=GE+ED≈1.3m.
答:此刻滑雪者头部G到斜坡AB的距离约为1.3m.
21.(8分)青岛方特梦幻王国位于美丽的山东省青岛市红岛海滨,由深圳华强集团投资兴建.火流星是其经典项目之一.如图所示,F→E→G为火流星过山车的一部分轨道,它可以看成一段抛物线.其中OE米,OF米(轨道厚度忽略不计).
(1)求抛物线F→E→G的函数关系式;
(2)在轨道距离地面5米处有两个位置P和G,当过山车运动到G处时,平行于地面向前运动了米至K点,又进入下坡段K→H(K接口处轨道忽略不计).已知轨道抛物线K→H→Q的形状与抛物线P→E→G完全相同,在G到Q的运动过程中,求OH的距离;
(3)现需要在轨道下坡段F→E进行一种安全加固,建造某种材料的水平和竖直支架AM、CM、BN、DN,且要求OA=AB.已知这种材料的价格是80000元/米,如何设计支架,会使造价最低?最低造价为多少元?
【考点】二次函数的应用.
【分析】(1)用待定系数法求函数解析式即可;
(2)先求出P,G坐标,再求出PG长度,通过抛物线K→H→Q的形状与抛物线P→E→G完全相同,平移长度为PG+GK,可得抛物线K→H→Q解析式,可得结论;
(3)先设出A,B横坐标,再代入解析式,分别求出M,N的纵坐标,然后求出AM,CM,BN,DN之和的最小值,从而求出最低造价.
【解答】解:(1)由图象可设抛物线解析式为y=a(x)2,
把F(0,)代入,得:
a(0)2,
解得:a,
∴抛物线F→E→G的函数关系式为y(x)2;
(2)当y=5时,5(x)2,
解得:x1,x2,
∴P(,5),G(,5),
∴PG5,
∵抛物线K→H→Q的形状与抛物线P→E→G完全相同,
∴抛物线K→H→Q由抛物线P→E→G向右平移(PG+GK)个单位,
∴抛物线K→H→Q为y2(x5)2(x﹣10)2,
令y=0,则x=10,
∴OH=10;
(3)设OA=AB=a,A(a,0),B(2a,0),
yM(a)2a2﹣5a,
yN(2a)2a2﹣10a,
∴l=AM+CM+BN+DN
5a+a10a2a
=4a2﹣12a
=4(a)2,
∵4>0,
∴开口向上,
∴当a时,l最短,最短为,
80000530000(元),
∴当OA=AB时,造价最低,最低造价为530000元.
22.(8分)解方程:x﹣2.
【考点】无理方程.
【分析】首先分别设,;将上述两式平方后相减,得到λ2﹣μ2=x﹣2;化简后得λ,代入上式并整理得到:3x2﹣8x﹣60=0,解该方程即可解决问题.
【解答】解:设,,
则λ2﹣μ2=﹣8x+16①;λ﹣μ=x﹣2②;
当x﹣2≠0时,由①÷②得:λ+μ=﹣8③,
由②+③得:2λ=x﹣10,λ,
∴,
整理得:3x2﹣8x﹣60=0,
解得:x1=6,x2,
经检验:x1=6,x2均是原方程的增根,
当x=2时,经检验x=2是方程的根,
∴x=2.
23.(8分)如图,AB是⊙O的直径,C是⊙O上一点,D是的中点,E为OD延长线上一点,且∠CAE=2∠C,AC与BD交于点H,与OE交于点F.
(1)求证:AE是⊙O的切线;
(2)若⊙O的半径10,,求线段DH的长.
【考点】相似三角形的判定与性质;解直角三角形;全等三角形的判定与性质;垂径定理;圆周角定理;切线的判定与性质.
【分析】(1)由垂径定理得出OD⊥AC,进而得出∠FAO+∠AOF=90°,由圆周角定理结合已知条件得出∠AOF=∠CAE,得出∠FAO+∠CAE=90°,即∠OAE=90°,即可证明AE是⊙O的切线;
(2)连接AD,利用解直角三角形得出tanB,设AD=3x,则BD=4x,AB=5x,由⊙O的半径10,得出AB=5x=20,求出x=4,求出AD=12,BD=16,继而证明△ADH∽△BDA,利用相似三角形的性质即可求出DH的长.
【解答】(1)证明:如图1,
∵D是的中点,
∴OD⊥AC,
∴∠AFO=90°,
∴∠FAO+∠AOF=90°,
∵∠AOF=2∠C,∠CAE=2∠C,
∴∠AOF=∠CAE,
∴∠FAO+∠CAE=90°,即∠OAE=90°,
∵OA是半径,
∴AE是⊙O的切线;
(2)解:如图2,连接AD,
∵∠C=∠B,,
tanB,
∵AB是直径,
∴∠ADB=90°,
∴tanB,
设AD=3x,则BD=4x,AB=5x,
∵⊙O的半径10,
∴AB=5x=20,
∴x=4,
∴AD=3×4=12,BD=4×4=16,
∵D是的中点,
∴AD=CD=12,
∴∠DAC=∠C,
∵∠B=∠C,
∴∠DAC=∠B,
∵∠ADH=∠BDA
∴△ADH∽△BDA,
∴,即,
∴DH=9.
24.(8分)二次函数y=x2+bx+c的图象与x轴交于点A(x1,0),B(x2,0)且x1≠x2.
(1)当x1=2,且b+c=﹣6时,
①求b,c的值;
②当t≤x≤t+2时,二次函数y=x2+bx+c的最小值为2t,求t的值;
(2)若x1=3x2,求证:.
【考点】二次函数综合题.
【分析】(1)①当x1=2,则抛物线过点A(2,0),且b+c=﹣6,于是得,解方程组求得b、c的值分别为2、﹣8;
②由y=x2+2x﹣8=(x+1)2﹣9,得该抛物线的顶点为(﹣1,﹣9),再分三种情况讨论,一是t+2≤﹣1,即t≤﹣3,则当x=t+2时,y最小=2t,于是得(t+2+1)2﹣9=2t;二是t<﹣1<t+2,即﹣3<t<﹣1,则当x=﹣1时,y最小=2t,于是得(﹣1+1)2﹣9=2t;三是t≥﹣1,则当x=t时,y最小=2t,于是得(t+1)2﹣9=2t,解方程求出相应的符合题意的t值即可;
(2)由x1=3x2,且x1≠x2,可证明x2≠0,由一元二次方程根与系数的关系得x1+x2=﹣b,则3x2+x2=﹣b,所以x2b,则(b)2+b (b)+c=0,可求得cb,则b﹣cbb2(b﹣4)2+3≤3.
【解答】(1)解:①当x1=2,则抛物线y=x2+bx+c经过点A(2,0),且b+c=﹣6,
∴,解得,
∴b、c的值分别为2、﹣8.
②∵y=x2+2x﹣8=(x+1)2﹣9,
∴该抛物线的顶点为(﹣1,﹣9),
若t+2≤﹣1,即t≤﹣3,如图1,当x=t+2时,y最小=2t,
∴(t+2+1)2﹣9=2t,
解得t1=﹣4,或t2=0(不符合题意,舍去);
若t<﹣1<t+2,即﹣3<t<﹣1,如图2,当x=﹣1时,y最小=2t,
∴(﹣1+1)2﹣9=2t,
解得t(不符合题意,舍去);
若t≥﹣1,如图3,当x=t时,y最小=2t,
∴(t+1)2﹣9=2t,
解得t1=2,t2=﹣2(不符合题意,舍去),
综上所述:t=4或t=2.
(2)证明:∵x1=3x2,且x1≠x2,
∴3x2≠x2,
∴x2≠0,
∵x1、x2是一元二次方程x2+bx+c=0的两个根,
∴x1+x2=﹣b,
∴3x2+x2=﹣b,
∴x2b,
∴(b)2+b (b)+c=0,
∴cb,
∴b﹣cbb2(b﹣4)2+3,
∵(b﹣4)2+3≤3,
∴b﹣c≤3.
25.(10分)(1)【探究发现】如图1,已知点O是正方形ABCD对角线的交点,点E是CB延长线上一点,作OF⊥OE交BA延长线于F点.小明探究发现,△EOF是等腰直角三角形.请证明这个结论.
(2)【模型应用】如图2,在(1)的结论下,延长DB、FE交于点P,若BC=6,BE=2,求BP的长.
(3)【拓展提升】如图3,若点G是正方形ABCD对角线BD上一点,DG=2BG,BC=6,点E在CB的延长线上运动时,连接EG,作FG⊥EG交直线AB于F点,设BE=x,记△EGF与正方形ABCD的重合面积为S,请直接写出S关于x的关系式.
【考点】四边形综合题.
【分析】(1)由正方形的性质得出∠AOB=90°,OA=OB,∠OAB=∠OBA=∠OBC=45°,证明△AOF≌△BOE(ASA),由全等三角形的性质得出OF=OE,则可得出结论;
(2)由勾股定理求出EF的长,证明△COE∽△FOP,由相似三角形的性质得出,求出OP的长,则可得出答案;
(3)过点G作GM⊥GB,则△GMB是等腰直角三角形,设EG交AB于点N,过点G作GH⊥AB于点H,求出BN,分两种情况,当0<x≤2时,S,当x>2时,设GF交DA于点P,求出PA,则可得出答案.
【解答】(1)证明:∵四边形ABCD是正方形,
∴∠AOB=90°,OA=OB,∠OAB=∠OBA=∠OBC=45°,
∴∠AOE+∠EOB=90°,∠OAF=∠OBE=135°,
∵OF⊥OE,
∴∠FOE=90°,
∴∠FOA+∠AOE=90°,
∴∠FOA=∠EOB,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(ASA),
∴OF=OE,
∵∠FOE=90°,
∴△OEF是等腰直角三角形;
(2)解:∵△AOF≌△BOE,
∴AF=BE,
∵BC=6,BE=2,
∴BF=AB+AF=8,CO=BO3,
在Rt△BEF中,EF2,
∵△FOE是等腰直角三角形,
∴OF=OEEF,∠OFP=45°,
∵∠OCE=∠OFP=45°,∠COE=∠COB+∠POE=90°+∠POE,∠FOP=∠FOE+∠POE=90°+∠POE,
∴∠COE=∠FOP,
∴△COE∽△FOP,
∴,
即,
∴OP,
∴PB=OP﹣OB;
(3)解:如图,过点G作GM⊥GB,则△GMB是等腰直角三角形,设EG交AB于点N,过点G作GH⊥AB于点H,
∴GM=GB,∠GBM=∠GMB=45°,
∴∠GBE=∠GMF=135°,
∵∠FGE=∠MGB=90°,
∴∠FGM=∠ECB,
∴△FGM≌△EGN(ASA),
∴FM=BE,∠GFM=∠GEB,
∵DG=2BG,BC=6,
∴GBBD2,
∴MB=24,
∵GH⊥MB,
∴MH=HB=GHMB=2,
∴AM=2,
∵BE=x,
∴FM=x,FH=FM+MH=x+2,
∵∠GFM=∠GEB,
∴tan∠GFM=tan∠GEB,
∴,
∴BN,
当0<x≤2时,SFN=FB﹣NB=x+4,
当x>2时,设GF交DA于点P,
∵∠GFM=∠PFA,
∴tan∠GFM=tan∠PFA,
即,
∴PA,
∴S△FGM﹣S△FAP=x+4,
综上所述,S.
26.(10分)已知点M(a,a+2)(a>0)在反比例函数的图象上,点H(0,1)在y轴上,连接MH,如图1,将MH绕着H点顺时针旋转90°至点M',点M'正好落在x轴上.
(1)求k的值和点M'的坐标;
(2)若点P在反比例函数图象上,连接HP并延长至点E,使得PE=PH,连接EM',PM',
①如图2,连接MP并延长交x轴于点Q,当PM′⊥x轴时,试说明EM′平分∠PM′Q;
②如图3,连接MM′交HE于点Q,将△MHM'沿着MM'翻折,记点H的对应点为H',若点H'恰好落在线段PE上,求△M′H′E与△PM′Q面积之比.
【考点】反比例函数综合题.
【分析】(1)过点M作MA⊥y轴于点A,由旋转性质得:∠MHM′=90°,HM=HM′,可证得△HMA≌△M′HO(AAS),得出AM=OH,OM′=AH,进而可得M(1,3),求得k=3,由AH=OM′=2,可得M′(2,0);
(2)①过点E作EF⊥x轴于点F,过点H作HG⊥EF于点G,则∠HGE=∠HGF=∠EFO=90°,由PM′⊥x轴,可得P(2,),∠PM′F=90°,由PE=PH,可得HG=4,由PD∥EG,可得△HPD∽△HEG,再证得△EFM′是等腰直角三角形,即∠EM′F=45°,可得EM′平分∠PM′Q;
②由旋转性质可得MM′⊥HH′,HQ=H′Q,证得四边形HMH′M′是正方形,得出Q(,),H′(3,2),运用待定系数法可得直线HE的解析式为yx+1,联立方程组可得P(,),进而得出E(33,),进而可得2.
【解答】(1)解:如图1,过点M作MA⊥y轴于点A,
则∠MAH=∠HOM′=90°,
∵将MH绕着H点顺时针旋转90°至点M',
∴∠MHM′=90°,HM=HM′,
∴∠AMH+∠AHM=∠OHM′+∠AHM=90°,
∴∠AMH=∠OHM′,
∴△HMA≌△M′HO(AAS),
∴AM=OH,OM′=AH,
∵H(0,1),M(a,a+2)(a>0),
∴OH=1,AM=a,
∴a=1,
∴M(1,3),
∴k=1×3=3,OA=3,
∴AH=OA﹣OH=3﹣1=2,
∴OM′=2,
∴M′(2,0);
(2)①证明:如图2,过点E作EF⊥x轴于点F,过点H作HG⊥EF于点G,
则∠HGE=∠HGF=∠EFO=90°,
∵M′(2,0),PM′⊥x轴,
∴P(2,),∠PM′F=90°,
∴PM′,
∵连接HP并延长至点E,使得PE=PH,
∴HG=4,
∵∠HOF=∠HGF=∠EFO=90°,
∴四边形FGHO是矩形,
∴FG=OH=1,OF=HG=4,
同理可得DM′=1,
∴PD=PM′﹣DM′1,
∵PD∥EG,
∴△HPD∽△HEG,
∴,
∴EG=2PD=21,
∴EF=EG+FG=1+1=2,
∵FM′=OF﹣OM′=4﹣2=2,
∴FM′=EF,
∵∠EFM′=90°,
∴△EFM′是等腰直角三角形,
∴∠EM′F=45°,
∴∠EM′F∠PM′F,
∴EM′平分∠PM′Q;
②解:∵将△MHM'沿着MM'翻折,点H的对应点为H'恰好落在线段PE上,
∴MM′⊥HH′,HQ=H′Q,
∵HM=HM′,
∴MQ=M′Q,
∵∠MHM′=90°,
∴四边形HMH′M′是正方形,
∵M(1,3),M′(2,0),
∴Q(,),
∵H(0,1),
∴H′(3,2),
设直线HE的解析式为y=kx+1,将Q(,)代入,得k+1,
解得:k,
∴直线HE的解析式为yx+1,
联立得x+1,
解得:x1(舍去),x2,
∴P(,),
∵PE=HP,
∴E(33,),
∵2,
∴2
数学模拟卷
一.选择题(共12小题,满分36分,每小题3分)
1.(3分)下列计算正确的是( )
A.(a﹣b)2=a2﹣b2 B.(﹣2a2)3=8a4
C.a3÷a2=a D.2a2+a2=3a4
2.(3分)陕西历史博物馆是中国第一座大型现代化国家级博物馆,2021年春节期间累计接待游客约37200人次,数据37200用科学记数法可表示为( )
A.372×102 B.3.72×103 C.3.72×104 D.0.372×105
3.(3分)下列计算正确的是( )
A.a+a2=a3 B.a6÷a3=a3
C.(﹣a2b)3=a6b3 D.(a+2)2=a2+4
4.(3分)化简分式后得( )
A. B. C. D.
5.(3分)已知二元一次方程组,则(x+y)(x﹣y)的值是( )
A.15 B.﹣5 C.5 D.﹣15
6.(3分)已知:关于x的一元二次方程x2﹣(R+r)xd2=0无实数根,其中R,r分别是⊙O1,⊙O2的半径,d为此两圆的圆心距,则⊙O1,⊙O2的位置关系为( )
A.外离 B.相切 C.相交 D.内含
7.(3分)如图所示,在梯形ABCD中,AB∥CD,∠ABC=α,∠BAD=β,则AD:BC等于( )
A. B. C. D.
8.(3分)如图,已知点O是等边△ABC三条高的交点,现将△AOB绕点O至少要旋转几度后与△BOC重合( )
A.60° B.120° C.240° D.360°
9.(3分)如图是边长为2的正方形及其内切圆和外接圆,则图中阴影部分的总面积为( )
A.3π﹣4 B.π+4 C.5π﹣4 D.3π+4
10.(3分)如图,在平面直角坐标系中,点O为坐标原点,在△ABC中,点C(﹣1,0).点A在x轴正半轴上,点B在第一象限内,∠ACB=30°,AC=AB=2,过点B作BD⊥x轴于点D,AE平分∠BAD交BD于点E,则点E的坐标( )
A. B.) C.(3,2) D.(3,1)
11.(3分)假设计算式“a#a+b”表示经过计算后a的值变为a的原值和b的原值的和:又“b#b c”表示经过计算后b的值变为b的原值和c的原值的乘积.假设计算开始时a=0,b=1,c=1.对a,b,c同时进行以下计算:(1)a#a+b;(2)b#b c;(3)c#a+b+c(即c的值变为所得到的a,b的值和c的原值的和).连续进行上述运算共三次,则计算结束时a,b,c三个数之和是( )
A.1位数 B.2位数 C.3位数 D.4位数
12.(3分)关于x的方程ax2+bx+c=0有两个不相等的实根x1,x2,若x2=2x1,则4b﹣3ac的最大值是( )
A.1 B.2 C.4 D.6
二.填空题(共6小题,满分15分)
13.(3分)如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=8,tan∠ABD,则线段AB的长为 .
14.(3分)关于x的方程()2=2,方程的所有的所有实根的和为 .
15.(3分)已知实数a,b满足a2+2a=b+2,b2+2b=a+2,则代数式的值等于 .
16.阅读材料:如果两个正数a、b,即a>0,b>0,则有下面的不等式,当且仅当a=b时取到等号.我们把叫做正数a、b算术平均数,把叫做正数a、b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具.根据上述材料,若,则y最小值为 .
17.(3分)若t为实数,x2﹣4x+t﹣2=0的两个非负实数根为a,b,则代数式(a2﹣1)(b2﹣1)的最小值
18.(3分)已知一次函数m与二次函数,若满足y1>0且y2<0时的自变量x的取值范围内有且只有一个整数,则m的取值范围是 .
三.解答题(共8小题,满分66分)
19.(6分)【阅读材料】:善于思考的小明在解方程组时,采用了一种“整体代换”的解法:解:将方程(2)变形:4x+10y+y=5,即2(2x+5y)+y=5(3),把方程(1)代入(3)得:2×3+y=5,所以y=﹣1,将y=﹣1代入(1)得x=4,所以原方程组的解为.
【解决问题】:
(1)模仿小明的“整体代换”法解方程组;
(2)已知x,y满足方程组,求x2+4y2的值.
20.(8分)2022年的冬天,越来越多的游客选择到山西九龙山滑雪场来放松一下自己,体验一下蓝蓝的天空,皑皑白雪的浪漫,重温一下儿时的激情和与大自然抗争的成就感,更能领略一下冬天滑雪的魅力.图1,图2分别是一名滑雪爱好者在滑雪过程中某一时刻的实景图与示意图,此时运动员的小腿ED与斜坡AB垂直,大腿EF与斜坡AB平行,G为头部,且G,E,D三点共线.若滑雪杖EM长为1m,EF=0.4m,∠EMD=30°,∠GFE=62°,求此时滑雪爱好者头部G到斜坡AB的距离.(精确到0.1m)(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
21.(8分)青岛方特梦幻王国位于美丽的山东省青岛市红岛海滨,由深圳华强集团投资兴建.火流星是其经典项目之一.如图所示,F→E→G为火流星过山车的一部分轨道,它可以看成一段抛物线.其中OE米,OF米(轨道厚度忽略不计).
(1)求抛物线F→E→G的函数关系式;
(2)在轨道距离地面5米处有两个位置P和G,当过山车运动到G处时,平行于地面向前运动了米至K点,又进入下坡段K→H(K接口处轨道忽略不计).已知轨道抛物线K→H→Q的形状与抛物线P→E→G完全相同,在G到Q的运动过程中,求OH的距离;
(3)现需要在轨道下坡段F→E进行一种安全加固,建造某种材料的水平和竖直支架AM、CM、BN、DN,且要求OA=AB.已知这种材料的价格是80000元/米,如何设计支架,会使造价最低?最低造价为多少元?
22.(8分)解方程:x﹣2.
23.(8分)如图,AB是⊙O的直径,C是⊙O上一点,D是的中点,E为OD延长线上一点,且∠CAE=2∠C,AC与BD交于点H,与OE交于点F.
(1)求证:AE是⊙O的切线;
(2)若⊙O的半径10,,求线段DH的长.
24.(8分)二次函数y=x2+bx+c的图象与x轴交于点A(x1,0),B(x2,0)且x1≠x2.
(1)当x1=2,且b+c=﹣6时,
①求b,c的值;
②当t≤x≤t+2时,二次函数y=x2+bx+c的最小值为2t,求t的值;
(2)若x1=3x2,求证:.
25.(10分)(1)【探究发现】如图1,已知点O是正方形ABCD对角线的交点,点E是CB延长线上一点,作OF⊥OE交BA延长线于F点.小明探究发现,△EOF是等腰直角三角形.请证明这个结论.
(2)【模型应用】如图2,在(1)的结论下,延长DB、FE交于点P,若BC=6,BE=2,求BP的长.
(3)【拓展提升】如图3,若点G是正方形ABCD对角线BD上一点,DG=2BG,BC=6,点E在CB的延长线上运动时,连接EG,作FG⊥EG交直线AB于F点,设BE=x,记△EGF与正方形ABCD的重合面积为S,请直接写出S关于x的关系式.
26.(10分)已知点M(a,a+2)(a>0)在反比例函数的图象上,点H(0,1)在y轴上,连接MH,如图1,将MH绕着H点顺时针旋转90°至点M',点M'正好落在x轴上.
(1)求k的值和点M'的坐标;
(2)若点P在反比例函数图象上,连接HP并延长至点E,使得PE=PH,连接EM',PM',
①如图2,连接MP并延长交x轴于点Q,当PM′⊥x轴时,试说明EM′平分∠PM′Q;
②如图3,连接MM′交HE于点Q,将△MHM'沿着MM'翻折,记点H的对应点为H',若点H'恰好落在线段PE上,求△M′H′E与△PM′Q面积之比.
2023-2024学年度新高一入学分班考试
数学模拟卷
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.(3分)下列计算正确的是( )
A.(a﹣b)2=a2﹣b2 B.(﹣2a2)3=8a4
C.a3÷a2=a D.2a2+a2=3a4
【考点】完全平方公式;合并同类项;幂的乘方与积的乘方;同底数幂的除法.
【分析】各式计算得到结果,即可作出判断.
【解答】解:A、原式=a2﹣2ab+b2,不符合题意;
B、原式=﹣8a6,不符合题意;
C、原式=a,符合题意;
D、原式=3a2,不符合题意.
故选:C.
2.(3分)陕西历史博物馆是中国第一座大型现代化国家级博物馆,2021年春节期间累计接待游客约37200人次,数据37200用科学记数法可表示为( )
A.372×102 B.3.72×103 C.3.72×104 D.0.372×105
【考点】科学记数法—表示较大的数.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
【解答】解:37200=3.72×104,
故选:C.
3.(3分)下列计算正确的是( )
A.a+a2=a3 B.a6÷a3=a3
C.(﹣a2b)3=a6b3 D.(a+2)2=a2+4
【考点】完全平方公式;合并同类项;幂的乘方与积的乘方;同底数幂的除法.
【分析】根据合并同类项法则,同底数幂的除法的运算法则,幂的乘方与积的乘方的运算法则,完全平方公式解答即可.
【解答】解:A、a与a2不是同类项,不能合并,原计算错误,故此选项不符合题意;
B、a6÷a3=a3,原计算正确,故此选项符合题意;
C、(﹣a2b)3=﹣a6b3,原计算错误,故此选项不符合题意;
D、(a+2)2=a2+4a+4,原计算错误,故此选项不符合题意.
故选:B.
4.(3分)化简分式后得( )
A. B. C. D.
【考点】约分.
【分析】先把分子和分母因式分解,再约分即可得出答案.
【解答】解:原式
.
故选:B.
5.(3分)已知二元一次方程组,则(x+y)(x﹣y)的值是( )
A.15 B.﹣5 C.5 D.﹣15
【考点】二元一次方程组的解;解二元一次方程组.
【分析】利用①﹣②可求出(x﹣y)的值,利用(①+②)÷3可求出(x+y)的值,从而可得答案.
【解答】解:,
①+②得:3x+3y=15,
∴x+y=5,
①﹣②得:x﹣y=﹣1,
∴(x+y)(x﹣y)=5×(﹣1)=﹣5,
故选:B.
6.(3分)已知:关于x的一元二次方程x2﹣(R+r)xd2=0无实数根,其中R,r分别是⊙O1,⊙O2的半径,d为此两圆的圆心距,则⊙O1,⊙O2的位置关系为( )
A.外离 B.相切 C.相交 D.内含
【考点】圆与圆的位置关系;根的判别式.
【分析】解答本题,先要根据题意得出根的判别式,然后再针对两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系,得出具体位置关系.
【解答】解:根据题意,方程无实数根,可得(R+r)2﹣d2<0,
则:(R+r+d)(R+r﹣d)<0,
因为R+r+d>0,所以R+r﹣d<0,
即:d>R+r,
那么,两圆外离.
故选:A.
7.(3分)如图所示,在梯形ABCD中,AB∥CD,∠ABC=α,∠BAD=β,则AD:BC等于( )
A. B. C. D.
【考点】解直角三角形;梯形.
【分析】分别过点D和点C作DE⊥AB交AB于点E,CF⊥AB交AB于点F,根据sinα,sinβ,将两者相比即可求出结果.
【解答】解:过点D和点C作DE⊥AB交AB于点E,CF⊥AB交AB于点F.
∵AB∥CD,
∴DE=CF.
在Rt△ADE中,sinβ;
在Rt△BCF中,sinα.
故.
故选:B.
8.(3分)如图,已知点O是等边△ABC三条高的交点,现将△AOB绕点O至少要旋转几度后与△BOC重合( )
A.60° B.120° C.240° D.360°
【考点】旋转的性质;等边三角形的性质.
【分析】先根据等边三角形的性质得出∠AOB=∠AOC=∠BOC=120°,再根据旋转的性质得出△AOB绕点O旋转后与△BOC重合至少要旋转的度数.
【解答】解:∵点O是等边△ABC三条高的交点,
∴∠AOB=∠AOC=∠BOC=120°,
∴由旋转的性质得出△AOB绕点O逆时针至少旋转120度后与△BOC重合.
故选:B.
9.(3分)如图是边长为2的正方形及其内切圆和外接圆,则图中阴影部分的总面积为( )
A.3π﹣4 B.π+4 C.5π﹣4 D.3π+4
【考点】正多边形和圆;扇形面积的计算;正方形的性质;三角形的内切圆与内心.
【分析】阴影部分的面积=大圆面积减去正方形面积+小圆面积.
【解答】解:阴影部分的面积=大圆面积减去正方形面积+小圆面积=π ()2﹣4+π 12=3π﹣4,
故选:A.
10.(3分)如图,在平面直角坐标系中,点O为坐标原点,在△ABC中,点C(﹣1,0).点A在x轴正半轴上,点B在第一象限内,∠ACB=30°,AC=AB=2,过点B作BD⊥x轴于点D,AE平分∠BAD交BD于点E,则点E的坐标( )
A. B.) C.(3,2) D.(3,1)
【考点】解直角三角形;坐标与图形性质.
【分析】由AB=AC可得∠ABC=∠ACB,则可求得∠BAD=60°,利用余弦可求得AD的长度,再由角平分线的定义可得∠EAD=30°,利用正切即可求DE的长度,从而可点E的坐标.
【解答】解:∵AC=AB=2,∠ACB=30°,
∴∠ABC=∠ACB=30°,
∴∠BAD=∠ABC+∠ACB=60°,
∵BD⊥x轴于点D,
∴cos∠BAD,
∴cos60°,
解得:AD,
∵AE平分∠BAD,
∴∠EAD=30°,
∴tan∠EAD,
即tan30°,
解得:DE=1,
∵点C(﹣1,0),
∴AO=AC﹣1=21,
∴OD=AO+AD=31,
∴点E的坐标为:(31,1).
故选:B.
11.(3分)假设计算式“a#a+b”表示经过计算后a的值变为a的原值和b的原值的和:又“b#b c”表示经过计算后b的值变为b的原值和c的原值的乘积.假设计算开始时a=0,b=1,c=1.对a,b,c同时进行以下计算:(1)a#a+b;(2)b#b c;(3)c#a+b+c(即c的值变为所得到的a,b的值和c的原值的和).连续进行上述运算共三次,则计算结束时a,b,c三个数之和是( )
A.1位数 B.2位数 C.3位数 D.4位数
【考点】规律型:数字的变化类.
【分析】读懂上述运算,理解新运算的规则,按照新规则对a、b、c同时进行连续三次运算,最后求和确定答案.
【解答】解:对a、b、c同时进行连续三次运算后的结果如下:
运算次数 1 2 3
a 1 2 5
b 1 3 24
c 3 8 37
经过三次运算后,a+b+c=5+24+37=66,它是一个两位数.
故选:B.
12.(3分)关于x的方程ax2+bx+c=0有两个不相等的实根x1,x2,若x2=2x1,则4b﹣3ac的最大值是( )
A.1 B.2 C.4 D.6
【考点】根与系数的关系;根的判别式.
【分析】根据根与系数的关系得出x1+x2,x1x2,由x2=2x1得出3x1,即x1,可解出x2,由两根之积可得acb2,代入代数式即可得到4b﹣3ac(b﹣3)2+6,从而求得4b﹣3ac的最大值是6.
【解答】解:∵关于x的方程ax2+bx+c=0有两个不相等的实根x1、x2,
∴x1+x2,x1x2,
∵x2=2x1,
∴3x1,即x1,
∴x2,
∴,
∴acb2,
∴4b﹣3ac=4b﹣3b2=4bb2(b﹣3)2+6,
∵0,
∴4b﹣3ac的最大值是6,
故选:D.
二.填空题(共6小题,满分15分)
13.(3分)如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=8,tan∠ABD,则线段AB的长为 5 .
【考点】菱形的性质;解直角三角形.
【分析】由菱形的性质得BO=ODBD=4,AC⊥BD,再由锐角三角函数定义求出OAOB=3,然后由勾股定理求出AB的长即可.
【解答】解:∵四边形ABCD为菱形,BD=8,
∴BO=ODBD=4,AC⊥BD,
∴∠AOB=90°,
∵tan∠ABD,
∴OAOB=3,
在Rt△ABC中,AO=3,OB=4,
∴AB5,
故答案为:5.
14.(3分)关于x的方程()2=2,方程的所有的所有实根的和为 .
【考点】换元法解分式方程.
【分析】可根据方程特点设y,则原方程可化为y+y2=2.解一元二次方程求y,再求x.
【解答】解:设y,则原方程可化为y+y2=2.解得y1=1,y2=﹣2,
当y1=1时,1,无解;
当y2=﹣2时,2,x,经检验x,是原方程的解.
故答案为.
15.(3分)已知实数a,b满足a2+2a=b+2,b2+2b=a+2,则代数式的值等于 2或7 .
【考点】根与系数的关系;分式的化简求值.
【分析】分两种情况:(1)当a=b时;(2)当a≠b时,联立方程组,运用加减消元法并结合完全平方公式,求得a2+b2和ab的值,然后将原式通分化简,代入求解.
【解答】解:(1)当a=b时,1+1=2;
(2)当a≠b时,联立方程组,
将①+②得:a2+b2+2a+2b=b+a+4,
整理得:a2+b2+a+b=4③,
将①﹣②得:a2﹣b2+2a﹣2b=b﹣a,
整理得:a2﹣b2+3a﹣3b=0,
(a+b)(a﹣b)+3(a﹣b)=0,
(a﹣b)(a+b+3)=0,
又∵a≠b,
∴a+b+3=0,即a+b=﹣3④,
将④代入③,得a2+b2﹣3=4,即a2+b2=7,
又∵(a+b)2=a2+2ab+b2=9,
∴ab=1,
∴7.
综上所述,代数式的值等于2或7.
故答案为:2或7.
16.阅读材料:如果两个正数a、b,即a>0,b>0,则有下面的不等式,当且仅当a=b时取到等号.我们把叫做正数a、b算术平均数,把叫做正数a、b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具.根据上述材料,若,则y最小值为 6 .
【考点】因式分解的应用;不等式的定义.
【分析】依据题意,读懂题目然后由公式可以得a+b≥2,从而y≥26,进而可以得解.
【解答】解:由题意,∵,
∴a+b≥2.
∵x>0,
∴3x>0,0,
∴y=3x226.
故答案为:6.
17.(3分)若t为实数,x2﹣4x+t﹣2=0的两个非负实数根为a,b,则代数式(a2﹣1)(b2﹣1)的最小值 ﹣15
【考点】根与系数的关系.
【分析】先根据根与系数的关系可得a+b=4,ab=t﹣2,将所求代数式化简代入可得结论.
【解答】解:∵x2﹣4x+t﹣2=0的两个非负实数根为a,b,
∴a+b=4,ab=t﹣2,Δ=16﹣4(t﹣2)≥0.
则,解得:2≤t≤6,
∴a2+b2=(a+b)2﹣2ab=42﹣2(t﹣2)=﹣2t+20,
∴(a2﹣1)(b2﹣1)=a2b2﹣(a2+b2)+1=(t﹣2)2+2t﹣20+1=t2﹣2t﹣15=(t﹣1)2﹣16,
∵2≤t≤6,
∴当t=2时,代数式(a2﹣1)(b2﹣1)有最小值,
∴代数式(a2﹣1)(b2﹣1)的最小值是1﹣16=﹣15,
故答案为:﹣15.
18.(3分)已知一次函数m与二次函数,若满足y1>0且y2<0时的自变量x的取值范围内有且只有一个整数,则m的取值范围是 m≤﹣1 .
【考点】抛物线与x轴的交点;一次函数的性质;二次函数的性质.
【分析】令y2=0可求出二次函数图象与x轴的交点坐标,进而可得出满足y2<0时自变量x的取值范围,结合满足y1>0且y2<0时的自变量x的取值范围内有且只有一个整数,即可得出关于m的一元一次不等式组,解之即可得出结论.
【解答】解:令y2=0,即x2﹣5x+4=0,
解得:x1=1,x2=4,
∴满足y2<0时自变量x的取值范围为1<x<4.
∵满足y1>0且y2<0时的自变量x的取值范围内有且只有一个整数,
∴,
∴m≤﹣1.
故答案为:m≤﹣1.
三.解答题(共8小题,满分66分)
19.(6分)【阅读材料】:善于思考的小明在解方程组时,采用了一种“整体代换”的解法:解:将方程(2)变形:4x+10y+y=5,即2(2x+5y)+y=5(3),把方程(1)代入(3)得:2×3+y=5,所以y=﹣1,将y=﹣1代入(1)得x=4,所以原方程组的解为.
【解决问题】:
(1)模仿小明的“整体代换”法解方程组;
(2)已知x,y满足方程组,求x2+4y2的值.
【考点】二元一次方程组的解;解二元一次方程组.
【分析】(1)将方程②化为3x+2(3x﹣2y)=19,再将方程①代入可求出x的值,进而求出方程组的解即可;
(2)将方程②×2,再与方程①相加后化简即可.
【解答】解:(1),
由②可得,3x+2(3x﹣2y)=19③,
将①代入③得,3x+10=19,
解得x=3,
把x=3代入①得,9﹣2y=5,
解得,y=2,
所以原方程组的解为;
(2),
②×2得,2x2+2xy+8y2=50③,
①+③得,5x2+20y2=100,
所以x2+4y2=20.
20.(8分)2022年的冬天,越来越多的游客选择到山西九龙山滑雪场来放松一下自己,体验一下蓝蓝的天空,皑皑白雪的浪漫,重温一下儿时的激情和与大自然抗争的成就感,更能领略一下冬天滑雪的魅力.图1,图2分别是一名滑雪爱好者在滑雪过程中某一时刻的实景图与示意图,此时运动员的小腿ED与斜坡AB垂直,大腿EF与斜坡AB平行,G为头部,且G,E,D三点共线.若滑雪杖EM长为1m,EF=0.4m,∠EMD=30°,∠GFE=62°,求此时滑雪爱好者头部G到斜坡AB的距离.(精确到0.1m)(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
【考点】解直角三角形的应用﹣坡度坡角问题.
【分析】连接GE,则GE⊥EF,GD=GE+ED,解直角△GEF,求出GE=EF tan62°≈0.752m,解直角△EDM,求出,代入GD=GE+ED,计算即可.
【解答】解:如图,连接GE′,
∵DE⊥AB且EF∥AB,
∴EF⊥GD,
则GE⊥EF,GD=GE+ED,
在直角△GEF中,
∵∠GEF=90°,∠GFE=62°,EF=0.4m,
∴GE=EF tan62°≈0.752m,
在直角△EDM中,
∵∠EDM=90°,∠EMD=30°,EM=1m,
∴,
∴GD=GE+ED≈1.3m.
答:此刻滑雪者头部G到斜坡AB的距离约为1.3m.
21.(8分)青岛方特梦幻王国位于美丽的山东省青岛市红岛海滨,由深圳华强集团投资兴建.火流星是其经典项目之一.如图所示,F→E→G为火流星过山车的一部分轨道,它可以看成一段抛物线.其中OE米,OF米(轨道厚度忽略不计).
(1)求抛物线F→E→G的函数关系式;
(2)在轨道距离地面5米处有两个位置P和G,当过山车运动到G处时,平行于地面向前运动了米至K点,又进入下坡段K→H(K接口处轨道忽略不计).已知轨道抛物线K→H→Q的形状与抛物线P→E→G完全相同,在G到Q的运动过程中,求OH的距离;
(3)现需要在轨道下坡段F→E进行一种安全加固,建造某种材料的水平和竖直支架AM、CM、BN、DN,且要求OA=AB.已知这种材料的价格是80000元/米,如何设计支架,会使造价最低?最低造价为多少元?
【考点】二次函数的应用.
【分析】(1)用待定系数法求函数解析式即可;
(2)先求出P,G坐标,再求出PG长度,通过抛物线K→H→Q的形状与抛物线P→E→G完全相同,平移长度为PG+GK,可得抛物线K→H→Q解析式,可得结论;
(3)先设出A,B横坐标,再代入解析式,分别求出M,N的纵坐标,然后求出AM,CM,BN,DN之和的最小值,从而求出最低造价.
【解答】解:(1)由图象可设抛物线解析式为y=a(x)2,
把F(0,)代入,得:
a(0)2,
解得:a,
∴抛物线F→E→G的函数关系式为y(x)2;
(2)当y=5时,5(x)2,
解得:x1,x2,
∴P(,5),G(,5),
∴PG5,
∵抛物线K→H→Q的形状与抛物线P→E→G完全相同,
∴抛物线K→H→Q由抛物线P→E→G向右平移(PG+GK)个单位,
∴抛物线K→H→Q为y2(x5)2(x﹣10)2,
令y=0,则x=10,
∴OH=10;
(3)设OA=AB=a,A(a,0),B(2a,0),
yM(a)2a2﹣5a,
yN(2a)2a2﹣10a,
∴l=AM+CM+BN+DN
5a+a10a2a
=4a2﹣12a
=4(a)2,
∵4>0,
∴开口向上,
∴当a时,l最短,最短为,
80000530000(元),
∴当OA=AB时,造价最低,最低造价为530000元.
22.(8分)解方程:x﹣2.
【考点】无理方程.
【分析】首先分别设,;将上述两式平方后相减,得到λ2﹣μ2=x﹣2;化简后得λ,代入上式并整理得到:3x2﹣8x﹣60=0,解该方程即可解决问题.
【解答】解:设,,
则λ2﹣μ2=﹣8x+16①;λ﹣μ=x﹣2②;
当x﹣2≠0时,由①÷②得:λ+μ=﹣8③,
由②+③得:2λ=x﹣10,λ,
∴,
整理得:3x2﹣8x﹣60=0,
解得:x1=6,x2,
经检验:x1=6,x2均是原方程的增根,
当x=2时,经检验x=2是方程的根,
∴x=2.
23.(8分)如图,AB是⊙O的直径,C是⊙O上一点,D是的中点,E为OD延长线上一点,且∠CAE=2∠C,AC与BD交于点H,与OE交于点F.
(1)求证:AE是⊙O的切线;
(2)若⊙O的半径10,,求线段DH的长.
【考点】相似三角形的判定与性质;解直角三角形;全等三角形的判定与性质;垂径定理;圆周角定理;切线的判定与性质.
【分析】(1)由垂径定理得出OD⊥AC,进而得出∠FAO+∠AOF=90°,由圆周角定理结合已知条件得出∠AOF=∠CAE,得出∠FAO+∠CAE=90°,即∠OAE=90°,即可证明AE是⊙O的切线;
(2)连接AD,利用解直角三角形得出tanB,设AD=3x,则BD=4x,AB=5x,由⊙O的半径10,得出AB=5x=20,求出x=4,求出AD=12,BD=16,继而证明△ADH∽△BDA,利用相似三角形的性质即可求出DH的长.
【解答】(1)证明:如图1,
∵D是的中点,
∴OD⊥AC,
∴∠AFO=90°,
∴∠FAO+∠AOF=90°,
∵∠AOF=2∠C,∠CAE=2∠C,
∴∠AOF=∠CAE,
∴∠FAO+∠CAE=90°,即∠OAE=90°,
∵OA是半径,
∴AE是⊙O的切线;
(2)解:如图2,连接AD,
∵∠C=∠B,,
tanB,
∵AB是直径,
∴∠ADB=90°,
∴tanB,
设AD=3x,则BD=4x,AB=5x,
∵⊙O的半径10,
∴AB=5x=20,
∴x=4,
∴AD=3×4=12,BD=4×4=16,
∵D是的中点,
∴AD=CD=12,
∴∠DAC=∠C,
∵∠B=∠C,
∴∠DAC=∠B,
∵∠ADH=∠BDA
∴△ADH∽△BDA,
∴,即,
∴DH=9.
24.(8分)二次函数y=x2+bx+c的图象与x轴交于点A(x1,0),B(x2,0)且x1≠x2.
(1)当x1=2,且b+c=﹣6时,
①求b,c的值;
②当t≤x≤t+2时,二次函数y=x2+bx+c的最小值为2t,求t的值;
(2)若x1=3x2,求证:.
【考点】二次函数综合题.
【分析】(1)①当x1=2,则抛物线过点A(2,0),且b+c=﹣6,于是得,解方程组求得b、c的值分别为2、﹣8;
②由y=x2+2x﹣8=(x+1)2﹣9,得该抛物线的顶点为(﹣1,﹣9),再分三种情况讨论,一是t+2≤﹣1,即t≤﹣3,则当x=t+2时,y最小=2t,于是得(t+2+1)2﹣9=2t;二是t<﹣1<t+2,即﹣3<t<﹣1,则当x=﹣1时,y最小=2t,于是得(﹣1+1)2﹣9=2t;三是t≥﹣1,则当x=t时,y最小=2t,于是得(t+1)2﹣9=2t,解方程求出相应的符合题意的t值即可;
(2)由x1=3x2,且x1≠x2,可证明x2≠0,由一元二次方程根与系数的关系得x1+x2=﹣b,则3x2+x2=﹣b,所以x2b,则(b)2+b (b)+c=0,可求得cb,则b﹣cbb2(b﹣4)2+3≤3.
【解答】(1)解:①当x1=2,则抛物线y=x2+bx+c经过点A(2,0),且b+c=﹣6,
∴,解得,
∴b、c的值分别为2、﹣8.
②∵y=x2+2x﹣8=(x+1)2﹣9,
∴该抛物线的顶点为(﹣1,﹣9),
若t+2≤﹣1,即t≤﹣3,如图1,当x=t+2时,y最小=2t,
∴(t+2+1)2﹣9=2t,
解得t1=﹣4,或t2=0(不符合题意,舍去);
若t<﹣1<t+2,即﹣3<t<﹣1,如图2,当x=﹣1时,y最小=2t,
∴(﹣1+1)2﹣9=2t,
解得t(不符合题意,舍去);
若t≥﹣1,如图3,当x=t时,y最小=2t,
∴(t+1)2﹣9=2t,
解得t1=2,t2=﹣2(不符合题意,舍去),
综上所述:t=4或t=2.
(2)证明:∵x1=3x2,且x1≠x2,
∴3x2≠x2,
∴x2≠0,
∵x1、x2是一元二次方程x2+bx+c=0的两个根,
∴x1+x2=﹣b,
∴3x2+x2=﹣b,
∴x2b,
∴(b)2+b (b)+c=0,
∴cb,
∴b﹣cbb2(b﹣4)2+3,
∵(b﹣4)2+3≤3,
∴b﹣c≤3.
25.(10分)(1)【探究发现】如图1,已知点O是正方形ABCD对角线的交点,点E是CB延长线上一点,作OF⊥OE交BA延长线于F点.小明探究发现,△EOF是等腰直角三角形.请证明这个结论.
(2)【模型应用】如图2,在(1)的结论下,延长DB、FE交于点P,若BC=6,BE=2,求BP的长.
(3)【拓展提升】如图3,若点G是正方形ABCD对角线BD上一点,DG=2BG,BC=6,点E在CB的延长线上运动时,连接EG,作FG⊥EG交直线AB于F点,设BE=x,记△EGF与正方形ABCD的重合面积为S,请直接写出S关于x的关系式.
【考点】四边形综合题.
【分析】(1)由正方形的性质得出∠AOB=90°,OA=OB,∠OAB=∠OBA=∠OBC=45°,证明△AOF≌△BOE(ASA),由全等三角形的性质得出OF=OE,则可得出结论;
(2)由勾股定理求出EF的长,证明△COE∽△FOP,由相似三角形的性质得出,求出OP的长,则可得出答案;
(3)过点G作GM⊥GB,则△GMB是等腰直角三角形,设EG交AB于点N,过点G作GH⊥AB于点H,求出BN,分两种情况,当0<x≤2时,S,当x>2时,设GF交DA于点P,求出PA,则可得出答案.
【解答】(1)证明:∵四边形ABCD是正方形,
∴∠AOB=90°,OA=OB,∠OAB=∠OBA=∠OBC=45°,
∴∠AOE+∠EOB=90°,∠OAF=∠OBE=135°,
∵OF⊥OE,
∴∠FOE=90°,
∴∠FOA+∠AOE=90°,
∴∠FOA=∠EOB,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(ASA),
∴OF=OE,
∵∠FOE=90°,
∴△OEF是等腰直角三角形;
(2)解:∵△AOF≌△BOE,
∴AF=BE,
∵BC=6,BE=2,
∴BF=AB+AF=8,CO=BO3,
在Rt△BEF中,EF2,
∵△FOE是等腰直角三角形,
∴OF=OEEF,∠OFP=45°,
∵∠OCE=∠OFP=45°,∠COE=∠COB+∠POE=90°+∠POE,∠FOP=∠FOE+∠POE=90°+∠POE,
∴∠COE=∠FOP,
∴△COE∽△FOP,
∴,
即,
∴OP,
∴PB=OP﹣OB;
(3)解:如图,过点G作GM⊥GB,则△GMB是等腰直角三角形,设EG交AB于点N,过点G作GH⊥AB于点H,
∴GM=GB,∠GBM=∠GMB=45°,
∴∠GBE=∠GMF=135°,
∵∠FGE=∠MGB=90°,
∴∠FGM=∠ECB,
∴△FGM≌△EGN(ASA),
∴FM=BE,∠GFM=∠GEB,
∵DG=2BG,BC=6,
∴GBBD2,
∴MB=24,
∵GH⊥MB,
∴MH=HB=GHMB=2,
∴AM=2,
∵BE=x,
∴FM=x,FH=FM+MH=x+2,
∵∠GFM=∠GEB,
∴tan∠GFM=tan∠GEB,
∴,
∴BN,
当0<x≤2时,SFN=FB﹣NB=x+4,
当x>2时,设GF交DA于点P,
∵∠GFM=∠PFA,
∴tan∠GFM=tan∠PFA,
即,
∴PA,
∴S△FGM﹣S△FAP=x+4,
综上所述,S.
26.(10分)已知点M(a,a+2)(a>0)在反比例函数的图象上,点H(0,1)在y轴上,连接MH,如图1,将MH绕着H点顺时针旋转90°至点M',点M'正好落在x轴上.
(1)求k的值和点M'的坐标;
(2)若点P在反比例函数图象上,连接HP并延长至点E,使得PE=PH,连接EM',PM',
①如图2,连接MP并延长交x轴于点Q,当PM′⊥x轴时,试说明EM′平分∠PM′Q;
②如图3,连接MM′交HE于点Q,将△MHM'沿着MM'翻折,记点H的对应点为H',若点H'恰好落在线段PE上,求△M′H′E与△PM′Q面积之比.
【考点】反比例函数综合题.
【分析】(1)过点M作MA⊥y轴于点A,由旋转性质得:∠MHM′=90°,HM=HM′,可证得△HMA≌△M′HO(AAS),得出AM=OH,OM′=AH,进而可得M(1,3),求得k=3,由AH=OM′=2,可得M′(2,0);
(2)①过点E作EF⊥x轴于点F,过点H作HG⊥EF于点G,则∠HGE=∠HGF=∠EFO=90°,由PM′⊥x轴,可得P(2,),∠PM′F=90°,由PE=PH,可得HG=4,由PD∥EG,可得△HPD∽△HEG,再证得△EFM′是等腰直角三角形,即∠EM′F=45°,可得EM′平分∠PM′Q;
②由旋转性质可得MM′⊥HH′,HQ=H′Q,证得四边形HMH′M′是正方形,得出Q(,),H′(3,2),运用待定系数法可得直线HE的解析式为yx+1,联立方程组可得P(,),进而得出E(33,),进而可得2.
【解答】(1)解:如图1,过点M作MA⊥y轴于点A,
则∠MAH=∠HOM′=90°,
∵将MH绕着H点顺时针旋转90°至点M',
∴∠MHM′=90°,HM=HM′,
∴∠AMH+∠AHM=∠OHM′+∠AHM=90°,
∴∠AMH=∠OHM′,
∴△HMA≌△M′HO(AAS),
∴AM=OH,OM′=AH,
∵H(0,1),M(a,a+2)(a>0),
∴OH=1,AM=a,
∴a=1,
∴M(1,3),
∴k=1×3=3,OA=3,
∴AH=OA﹣OH=3﹣1=2,
∴OM′=2,
∴M′(2,0);
(2)①证明:如图2,过点E作EF⊥x轴于点F,过点H作HG⊥EF于点G,
则∠HGE=∠HGF=∠EFO=90°,
∵M′(2,0),PM′⊥x轴,
∴P(2,),∠PM′F=90°,
∴PM′,
∵连接HP并延长至点E,使得PE=PH,
∴HG=4,
∵∠HOF=∠HGF=∠EFO=90°,
∴四边形FGHO是矩形,
∴FG=OH=1,OF=HG=4,
同理可得DM′=1,
∴PD=PM′﹣DM′1,
∵PD∥EG,
∴△HPD∽△HEG,
∴,
∴EG=2PD=21,
∴EF=EG+FG=1+1=2,
∵FM′=OF﹣OM′=4﹣2=2,
∴FM′=EF,
∵∠EFM′=90°,
∴△EFM′是等腰直角三角形,
∴∠EM′F=45°,
∴∠EM′F∠PM′F,
∴EM′平分∠PM′Q;
②解:∵将△MHM'沿着MM'翻折,点H的对应点为H'恰好落在线段PE上,
∴MM′⊥HH′,HQ=H′Q,
∵HM=HM′,
∴MQ=M′Q,
∵∠MHM′=90°,
∴四边形HMH′M′是正方形,
∵M(1,3),M′(2,0),
∴Q(,),
∵H(0,1),
∴H′(3,2),
设直线HE的解析式为y=kx+1,将Q(,)代入,得k+1,
解得:k,
∴直线HE的解析式为yx+1,
联立得x+1,
解得:x1(舍去),x2,
∴P(,),
∵PE=HP,
∴E(33,),
∵2,
∴2
同课章节目录
