第二十四章 圆单元练习题(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第二十四章 圆 单元练习 2023-2024学年人教版九年级数学上册(含解析)
一、单选题
1.(2023秋·河北保定·九年级校考期末)“易有太极,始生两仪,两仪生四象,四象生八卦”,太极图是我国古代文化关于太极思想的图示,内含表示一阴一阳的图形(一黑一白).如图,在正方形的内切圆中画出太极图,然后在正方形内随机取一点,则此点取自太极图中黑色部分的概率是( )
A. B. C. D.
2.(2023秋·河南省直辖县级单位·九年级校联考期末)如图,的半径为,弦的长为,P是弦上一动点,则线段长的最小值为( )
A.10 B. C.5 D.
3.(2022秋·内蒙古巴彦淖尔·九年级校考期末)如图,为的直径,点是的中点,过点作于点,延长交于点.若,,则的直径长为( )
A. B. C. D.
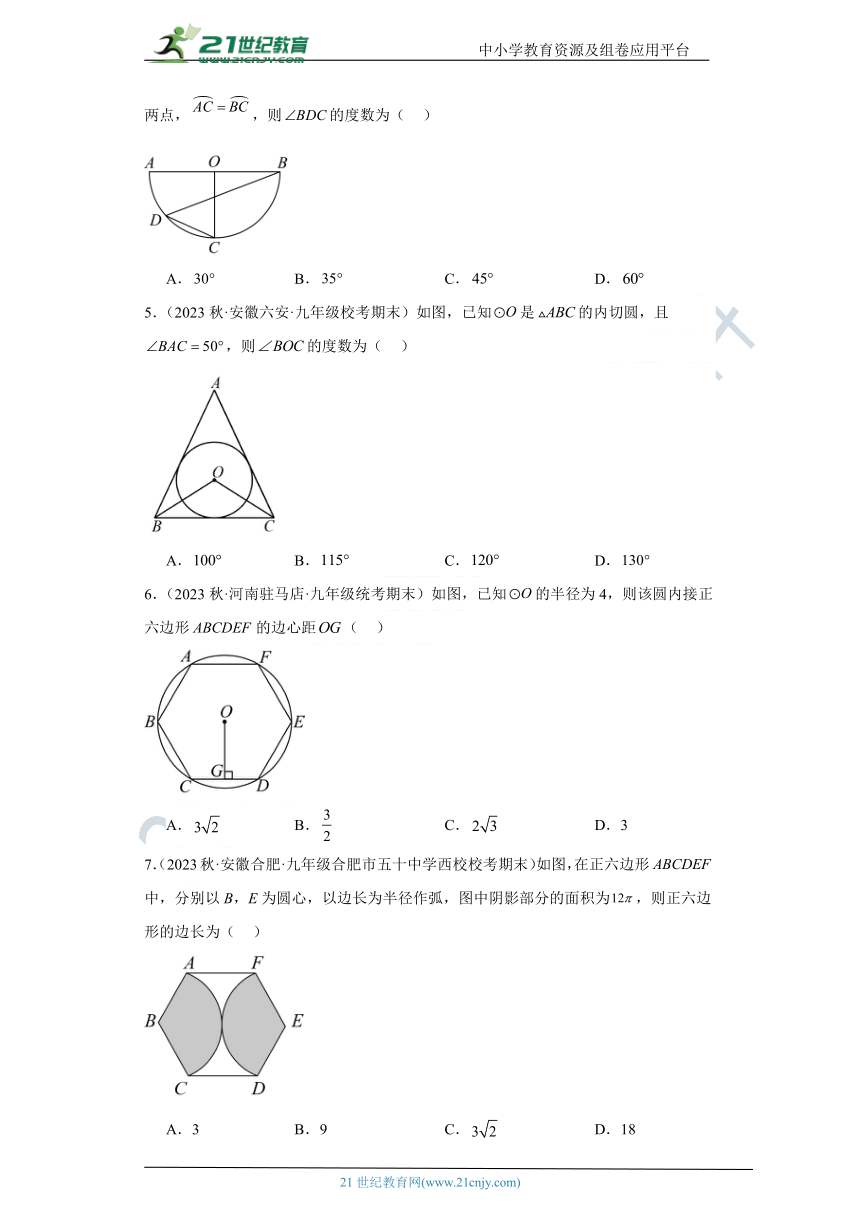
4.(2023秋·辽宁葫芦岛·九年级统考期末)如图,以为直径的半圆上有,的两点,,则的度数为( )
A. B. C. D.
5.(2023秋·安徽六安·九年级校考期末)如图,已知是的内切圆,且,则的度数为( )
A. B. C. D.
6.(2023秋·河南驻马店·九年级统考期末)如图,已知的半径为4,则该圆内接正六边形的边心距( )
A. B. C. D.3
7.(2023秋·安徽合肥·九年级合肥市五十中学西校校考期末)如图,在正六边形中,分别以B,E为圆心,以边长为半径作弧,图中阴影部分的面积为,则正六边形的边长为( )
A.3 B.9 C. D.18
二、填空题
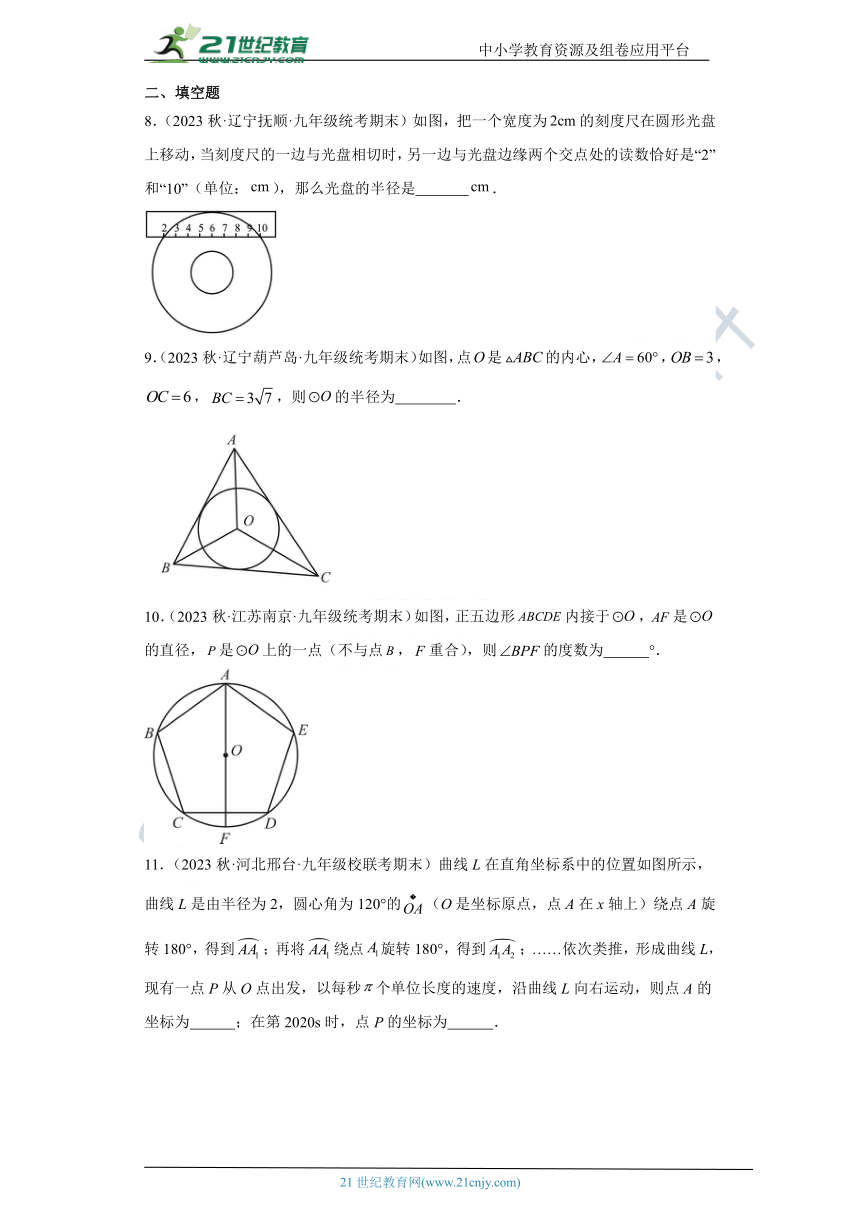
8.(2023秋·辽宁抚顺·九年级统考期末)如图,把一个宽度为的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:),那么光盘的半径是 .
9.(2023秋·辽宁葫芦岛·九年级统考期末)如图,点是的内心,,,,,则的半径为 .
10.(2023秋·江苏南京·九年级统考期末)如图,正五边形内接于,是的直径,是上的一点(不与点,重合),则的度数为 °.
11.(2023秋·河北邢台·九年级校联考期末)曲线L在直角坐标系中的位置如图所示,曲线L是由半径为2,圆心角为120°的(O是坐标原点,点A在x轴上)绕点A旋转180°,得到;再将绕点旋转180°,得到;……依次类推,形成曲线L,现有一点P从O点出发,以每秒个单位长度的速度,沿曲线L向右运动,则点A的坐标为 ;在第2020s时,点P的坐标为 .
三、解答题
12.(2023秋·河南信阳·九年级校联考期末)如图,正方形网格中,每个小正方形的边长都是一个 位长度,在平面直角坐标系内,的三个顶点坐标分别为.
(1)画出关于轴对称的;
(2)画出绕点O逆时针旋转后的;
(3)在(2)的条件下,求点旋转到经过的路径长(结果保).
13.(2023秋·江苏宿迁·九年级统考期末)如图,四边形是的内接四边形,且,垂足为,是的直径.
(1)和相等吗?为什么?
(2)过圆心作,垂足为,若,求的长.
14.(2023秋·四川南充·九年级四川省南充高级中学校考期末)如图,在中,,的平分线交于点D,点O在上,以点O为圆心,为半径的圆恰好经过点D,分别交,于点E,F.
(1)试判断直线与的位置关系,并说明理由;
(2)若,,,求阴影部分的面积(结果保留).
15.(2023秋·河北邯郸·九年级统考期末)如图,的半径为4,将该圆等分成8份,连接,并延长交于点.
(1)连接,直接写出和的位置关系___________;
(2)求证:;
(3)求的长;
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】为了方便求解令正方形的边长为1,那么圆的直径也就是1,可以表示出正方形和圆的面积,利用图形的对称性可以得到太极图黑色和白色部分各占圆的一半,这样就能得出最后结果.
【详解】设正方形边长为1,
正方形面积,
圆的直径为1,则半径为,
圆的面积,
太极图是旋转对称图形,所以黑色和白色部分各占圆面积的一半,
太极图黑色部分面积,
所求概率为.
故选B.
【点睛】本题考查了内切圆的知识,圆和正方形的面积,以及旋转图形的对称性,利用对称性得出黑色部分占太极图的一半是解答本题的关键.
2.D
【分析】过O点作于H,连接,如图,根据垂径定理得到,再利用勾股定理计算出,然后根据垂线段最短求解.
【详解】解:过O点作于H,连接,如图,
∴,
在中,,
∴线段长的最小值为.
故选:D.
【点睛】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了垂线段最短.
3.B
【分析】连接,首先证明,设,在中,利用勾股定理构建方程即可解决问题
【详解】解:如图,连接.
,
,,
点D是弧的中点,
,
,
,
,
设,
在中,则有,
解得,
,
故选:B.
【点睛】本题考查勾股定理,垂径定理,弧,弦之间的关系等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
4.C
【分析】利用同弧所对的圆心角和圆周角之间的关系即可解答.
【详解】,
,
,
故选C.
【点睛】该题考查了圆心角和圆周角定理,解答该题的关键是清楚同弧所对的圆周角等于圆心角的一半.
5.B
【分析】由三角形内切圆定义可知、是、的角平分线,所以可得到关系式,把对应数值代入即可求得的值.
【详解】解:∵是的内切圆,
、是、的角平分线,
,
.
故选:B.
【点睛】此题主要考查了三角形的内切圆.关键是要知道三角形内切圆的圆心是三角形三个内角平分线的交点.
6.C
【分析】连接,,可得是等边三角形,根据边心距即为等边三角形的高用勾股定理求出.
【详解】解:连接,,
∵六边形是正六边形,
∴,
∴是等边三角形,
由题意可知,则垂直平分,
∴,
∴
故选:C.
【点睛】本题考查了正多边形,等边三角形的判定及性质,熟练掌握圆内接正多边形的相关概念是解题的关键.
7.C
【分析】根据多边形的内角和公式求出扇形的圆心角,然后按扇形面积公式计算即可.
【详解】解:∵正六边形的内角是,阴影部分的面积为,
设正六边形的边长为r,
∴,
解得.
则正六边形的边长为.
故选:C.
【点睛】本题考查了扇形面积的计算.本题的关键是根据多边形的内角和公式求出扇形的圆心角.
8.5
【分析】设光盘的圆心为O,过点O作垂直直尺于点A,连接,再设,利用勾股定理求出x的值即可.
【详解】解:设光盘的圆心为O,如图所示:
过点O作垂直直尺于点A,连接,再设,
∵一边与光盘边缘两个交点处的读数恰好是“2”和“10”,
∴,
∵刻度尺宽,
∴,
在中,
,即,
解得:.
故答案为:5.
【点睛】本题考查了垂径定理,以及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
9.
【分析】过O作交于E,设,在和中,运用勾股定理即可解答;
【详解】过O作交于E,设
点是的内心,,,
在中,由勾股定理可得:
在中,由勾股定理可得:
故
解得
故
故答案为
【点睛】该题主要考查了角平分线的性质,勾股定理,圆的基本性质,解答该题的关键是掌握该部分知识点.
10.或/或
【分析】根据正五边形的性质和圆周角定理,分当点在劣弧上时和当点在优弧上时,结合图形求解即可.
【详解】①如图所示:当点在劣弧上时,
连接、、,
∵是正五边形,是的直径,
∵是正五边形,
∴,
∵是的直径,
∴,
∵,
∴,
∴,
∴,
∴(为优弧所对的圆心角)
∴;
②如图所示:当点在优弧上时,连接、、,
∵是正五边形,
∴,
∵是的直径,
∴,
∵,
∴,
∴,
∴,
∴;
故答案为:或 .
【点睛】本题主要考查正五边形的性质、圆周角定理,熟练掌握相关知识点是解题的关键.
11.
【分析】如图,设的圆心为,过点作于.解直角三角形求出的长,即可得到点坐标,再求出点的运动路径,判断出点的位置,求出可得结论.
【详解】解:如图,设的圆心为,过点作于.
由题意,,
,
,,
,
,
,
的长,点的运动路径,
又,
点在轴上,的长,
此时.
故答案为,.
【点睛】本题考查弧长公式,规律型问题,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.
12.(1)见解析
(2)见解析
(3)
【分析】(1)利用轴对称的性质画出图形即可;
(2)利用旋转变换的性质画出图形即可;
(3)点B旋转到经过的路径长即为圆弧长,根据弧长公式计算即可;
【详解】(1)关于x轴对称的如下图所示;
(2)绕点O逆时针旋转后的如上图所示;
(3)如上图,扇形的半径.
则扇形的弧长为:
即B点旋转到经过的路径长为
【点睛】本题考查了利用轴对称和旋转变换作图,扇形弧长公式等知识,熟练掌握网格结构准确找出对应点的位置是解题的关键.
13.(1)相等,理由见解析
(2)10
【分析】(1)根据是的直径得到,又由垂线定义得,利用等角的余角相等证明即可;
(2)由垂径定理得,再由三角形的中位线性质求得,进而即可求解.
【详解】(1)解:连接,
是的直径,
,
,
,
.
(2)解:,
,
,
,
,
.
【点睛】本题考查的是圆周角定理,等角的余角相等,圆心角、弦的关系,三角形的中位线性质,垂径定理,掌握圆心角、弦的关系,三角形的中位线性质以及垂径定理是解题的关键.
14.(1)与相切
(2)
【分析】(1)连接,证明,即可证得,从而证得是圆的切线;
(2)在中,设,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为圆的半径,求出圆心角的度数,的面积减去扇形面积即可确定出阴影部分面积.
【详解】(1)证明:连接,如下图所示,
∵是的平分线,
∴,
又∵,
∴,
∴,
∴,
∴,即,
又∵过半径的外端点D,
∴与相切;
(2)解:设,则,
根据勾股定理得:,即,
解得,即,
∴,
∵在中,,
∴,
∴,
∴,
则阴影部分的面积是,
故阴影部分的面积是.
【点睛】本题考查了切线的判定,扇形面积,以及勾股定理,熟练掌握切线的判定是解本题的关键.
15.(1)
(2)见解析
(3)
【分析】(1)连接,根据将该圆等分成8份,可得是的直径,再根据圆周角定理可证得;
(2)连接,,根据圆周角定理可证得,再由被8等分可得,,即可证得,再根据全等三角形的性质,即可证得结论;
(3)连接,,,由被8等分可求得,可得,再根据勾股定理即可求解.
【详解】(1)解:如图:连接,
将该圆等分成8份,
是的直径,
,
,
故答案为:;
(2)解:如图:连接,,
,
被8等分,
,,
在与中,
∴,
,
,即;
(3)解:如图:连接,,,
被8等分,
∴,
,
,
∴在中,.
【点睛】本题考查了圆周角定理,等分圆的性质,全等三角形的性质及判定定理,勾股定理,作出辅助线是解决本题的关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
第二十四章 圆 单元练习 2023-2024学年人教版九年级数学上册(含解析)
一、单选题
1.(2023秋·河北保定·九年级校考期末)“易有太极,始生两仪,两仪生四象,四象生八卦”,太极图是我国古代文化关于太极思想的图示,内含表示一阴一阳的图形(一黑一白).如图,在正方形的内切圆中画出太极图,然后在正方形内随机取一点,则此点取自太极图中黑色部分的概率是( )
A. B. C. D.
2.(2023秋·河南省直辖县级单位·九年级校联考期末)如图,的半径为,弦的长为,P是弦上一动点,则线段长的最小值为( )
A.10 B. C.5 D.
3.(2022秋·内蒙古巴彦淖尔·九年级校考期末)如图,为的直径,点是的中点,过点作于点,延长交于点.若,,则的直径长为( )
A. B. C. D.
4.(2023秋·辽宁葫芦岛·九年级统考期末)如图,以为直径的半圆上有,的两点,,则的度数为( )
A. B. C. D.
5.(2023秋·安徽六安·九年级校考期末)如图,已知是的内切圆,且,则的度数为( )
A. B. C. D.
6.(2023秋·河南驻马店·九年级统考期末)如图,已知的半径为4,则该圆内接正六边形的边心距( )
A. B. C. D.3
7.(2023秋·安徽合肥·九年级合肥市五十中学西校校考期末)如图,在正六边形中,分别以B,E为圆心,以边长为半径作弧,图中阴影部分的面积为,则正六边形的边长为( )
A.3 B.9 C. D.18
二、填空题
8.(2023秋·辽宁抚顺·九年级统考期末)如图,把一个宽度为的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:),那么光盘的半径是 .
9.(2023秋·辽宁葫芦岛·九年级统考期末)如图,点是的内心,,,,,则的半径为 .
10.(2023秋·江苏南京·九年级统考期末)如图,正五边形内接于,是的直径,是上的一点(不与点,重合),则的度数为 °.
11.(2023秋·河北邢台·九年级校联考期末)曲线L在直角坐标系中的位置如图所示,曲线L是由半径为2,圆心角为120°的(O是坐标原点,点A在x轴上)绕点A旋转180°,得到;再将绕点旋转180°,得到;……依次类推,形成曲线L,现有一点P从O点出发,以每秒个单位长度的速度,沿曲线L向右运动,则点A的坐标为 ;在第2020s时,点P的坐标为 .
三、解答题
12.(2023秋·河南信阳·九年级校联考期末)如图,正方形网格中,每个小正方形的边长都是一个 位长度,在平面直角坐标系内,的三个顶点坐标分别为.
(1)画出关于轴对称的;
(2)画出绕点O逆时针旋转后的;
(3)在(2)的条件下,求点旋转到经过的路径长(结果保).
13.(2023秋·江苏宿迁·九年级统考期末)如图,四边形是的内接四边形,且,垂足为,是的直径.
(1)和相等吗?为什么?
(2)过圆心作,垂足为,若,求的长.
14.(2023秋·四川南充·九年级四川省南充高级中学校考期末)如图,在中,,的平分线交于点D,点O在上,以点O为圆心,为半径的圆恰好经过点D,分别交,于点E,F.
(1)试判断直线与的位置关系,并说明理由;
(2)若,,,求阴影部分的面积(结果保留).
15.(2023秋·河北邯郸·九年级统考期末)如图,的半径为4,将该圆等分成8份,连接,并延长交于点.
(1)连接,直接写出和的位置关系___________;
(2)求证:;
(3)求的长;
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】为了方便求解令正方形的边长为1,那么圆的直径也就是1,可以表示出正方形和圆的面积,利用图形的对称性可以得到太极图黑色和白色部分各占圆的一半,这样就能得出最后结果.
【详解】设正方形边长为1,
正方形面积,
圆的直径为1,则半径为,
圆的面积,
太极图是旋转对称图形,所以黑色和白色部分各占圆面积的一半,
太极图黑色部分面积,
所求概率为.
故选B.
【点睛】本题考查了内切圆的知识,圆和正方形的面积,以及旋转图形的对称性,利用对称性得出黑色部分占太极图的一半是解答本题的关键.
2.D
【分析】过O点作于H,连接,如图,根据垂径定理得到,再利用勾股定理计算出,然后根据垂线段最短求解.
【详解】解:过O点作于H,连接,如图,
∴,
在中,,
∴线段长的最小值为.
故选:D.
【点睛】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了垂线段最短.
3.B
【分析】连接,首先证明,设,在中,利用勾股定理构建方程即可解决问题
【详解】解:如图,连接.
,
,,
点D是弧的中点,
,
,
,
,
设,
在中,则有,
解得,
,
故选:B.
【点睛】本题考查勾股定理,垂径定理,弧,弦之间的关系等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
4.C
【分析】利用同弧所对的圆心角和圆周角之间的关系即可解答.
【详解】,
,
,
故选C.
【点睛】该题考查了圆心角和圆周角定理,解答该题的关键是清楚同弧所对的圆周角等于圆心角的一半.
5.B
【分析】由三角形内切圆定义可知、是、的角平分线,所以可得到关系式,把对应数值代入即可求得的值.
【详解】解:∵是的内切圆,
、是、的角平分线,
,
.
故选:B.
【点睛】此题主要考查了三角形的内切圆.关键是要知道三角形内切圆的圆心是三角形三个内角平分线的交点.
6.C
【分析】连接,,可得是等边三角形,根据边心距即为等边三角形的高用勾股定理求出.
【详解】解:连接,,
∵六边形是正六边形,
∴,
∴是等边三角形,
由题意可知,则垂直平分,
∴,
∴
故选:C.
【点睛】本题考查了正多边形,等边三角形的判定及性质,熟练掌握圆内接正多边形的相关概念是解题的关键.
7.C
【分析】根据多边形的内角和公式求出扇形的圆心角,然后按扇形面积公式计算即可.
【详解】解:∵正六边形的内角是,阴影部分的面积为,
设正六边形的边长为r,
∴,
解得.
则正六边形的边长为.
故选:C.
【点睛】本题考查了扇形面积的计算.本题的关键是根据多边形的内角和公式求出扇形的圆心角.
8.5
【分析】设光盘的圆心为O,过点O作垂直直尺于点A,连接,再设,利用勾股定理求出x的值即可.
【详解】解:设光盘的圆心为O,如图所示:
过点O作垂直直尺于点A,连接,再设,
∵一边与光盘边缘两个交点处的读数恰好是“2”和“10”,
∴,
∵刻度尺宽,
∴,
在中,
,即,
解得:.
故答案为:5.
【点睛】本题考查了垂径定理,以及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
9.
【分析】过O作交于E,设,在和中,运用勾股定理即可解答;
【详解】过O作交于E,设
点是的内心,,,
在中,由勾股定理可得:
在中,由勾股定理可得:
故
解得
故
故答案为
【点睛】该题主要考查了角平分线的性质,勾股定理,圆的基本性质,解答该题的关键是掌握该部分知识点.
10.或/或
【分析】根据正五边形的性质和圆周角定理,分当点在劣弧上时和当点在优弧上时,结合图形求解即可.
【详解】①如图所示:当点在劣弧上时,
连接、、,
∵是正五边形,是的直径,
∵是正五边形,
∴,
∵是的直径,
∴,
∵,
∴,
∴,
∴,
∴(为优弧所对的圆心角)
∴;
②如图所示:当点在优弧上时,连接、、,
∵是正五边形,
∴,
∵是的直径,
∴,
∵,
∴,
∴,
∴,
∴;
故答案为:或 .
【点睛】本题主要考查正五边形的性质、圆周角定理,熟练掌握相关知识点是解题的关键.
11.
【分析】如图,设的圆心为,过点作于.解直角三角形求出的长,即可得到点坐标,再求出点的运动路径,判断出点的位置,求出可得结论.
【详解】解:如图,设的圆心为,过点作于.
由题意,,
,
,,
,
,
,
的长,点的运动路径,
又,
点在轴上,的长,
此时.
故答案为,.
【点睛】本题考查弧长公式,规律型问题,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.
12.(1)见解析
(2)见解析
(3)
【分析】(1)利用轴对称的性质画出图形即可;
(2)利用旋转变换的性质画出图形即可;
(3)点B旋转到经过的路径长即为圆弧长,根据弧长公式计算即可;
【详解】(1)关于x轴对称的如下图所示;
(2)绕点O逆时针旋转后的如上图所示;
(3)如上图,扇形的半径.
则扇形的弧长为:
即B点旋转到经过的路径长为
【点睛】本题考查了利用轴对称和旋转变换作图,扇形弧长公式等知识,熟练掌握网格结构准确找出对应点的位置是解题的关键.
13.(1)相等,理由见解析
(2)10
【分析】(1)根据是的直径得到,又由垂线定义得,利用等角的余角相等证明即可;
(2)由垂径定理得,再由三角形的中位线性质求得,进而即可求解.
【详解】(1)解:连接,
是的直径,
,
,
,
.
(2)解:,
,
,
,
,
.
【点睛】本题考查的是圆周角定理,等角的余角相等,圆心角、弦的关系,三角形的中位线性质,垂径定理,掌握圆心角、弦的关系,三角形的中位线性质以及垂径定理是解题的关键.
14.(1)与相切
(2)
【分析】(1)连接,证明,即可证得,从而证得是圆的切线;
(2)在中,设,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为圆的半径,求出圆心角的度数,的面积减去扇形面积即可确定出阴影部分面积.
【详解】(1)证明:连接,如下图所示,
∵是的平分线,
∴,
又∵,
∴,
∴,
∴,
∴,即,
又∵过半径的外端点D,
∴与相切;
(2)解:设,则,
根据勾股定理得:,即,
解得,即,
∴,
∵在中,,
∴,
∴,
∴,
则阴影部分的面积是,
故阴影部分的面积是.
【点睛】本题考查了切线的判定,扇形面积,以及勾股定理,熟练掌握切线的判定是解本题的关键.
15.(1)
(2)见解析
(3)
【分析】(1)连接,根据将该圆等分成8份,可得是的直径,再根据圆周角定理可证得;
(2)连接,,根据圆周角定理可证得,再由被8等分可得,,即可证得,再根据全等三角形的性质,即可证得结论;
(3)连接,,,由被8等分可求得,可得,再根据勾股定理即可求解.
【详解】(1)解:如图:连接,
将该圆等分成8份,
是的直径,
,
,
故答案为:;
(2)解:如图:连接,,
,
被8等分,
,,
在与中,
∴,
,
,即;
(3)解:如图:连接,,,
被8等分,
∴,
,
,
∴在中,.
【点睛】本题考查了圆周角定理,等分圆的性质,全等三角形的性质及判定定理,勾股定理,作出辅助线是解决本题的关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
