平均数(课件)-五年级上册数学沪教版(共19张PPT)
文档属性
| 名称 | 平均数(课件)-五年级上册数学沪教版(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-11 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
平均数
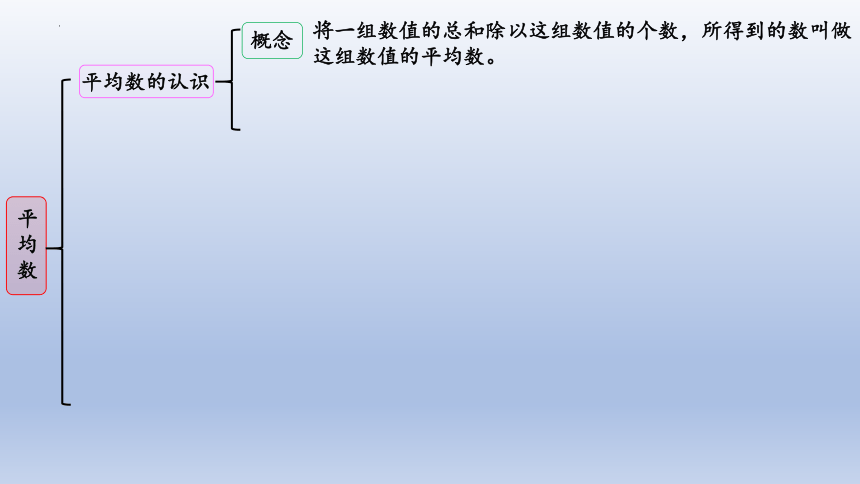
平均数的认识
将一组数值的总和除以这组数值的个数,所得到的数叫做这组数值的平均数。
平均数
概念
判断
(1)游泳池平均水深1.2米,小胖不会游泳,他身高1.45米,所以在游泳池中玩耍肯定安全。( )
(2)五(1)班学生平均身高155厘米,李强是其中最高的队员,他的身高是154厘米。( )
×
×
平均数能较好地反映一组数据的总体情况,不代表个体。
平均数处于这组数值的最大值和最小值之间。
平均数的认识
将一组数值的总和除以这组数值的个数,所得到的数叫做这组数值的平均数。
平均数
平均数能较好地反映一组数据的总体情况,不代表个体。
概念
特点
平均数处于这组数值的最大值和最小值之间。
平均数的计算
平均数=总和÷个数
方法
总和=平均数×个数
只列式,不计算。
1、某煤场7天产煤1.26万吨,平均每天产煤多少万吨?
1.26÷7
2、某煤场一周前3天产煤0.48万吨,后4天产煤0.78万吨,平均每天产煤多少万吨?
(0.48+0.78)÷(3+4)
3、某煤场一周前3天产煤0.48万吨,后4天每天产煤0.195万吨,平均每天产煤多少万吨?
(0.48+0.195×4)÷(3+4)
4、某煤场一周前3天每天产煤0.16万吨,后4天每天产煤0.195万吨,平均每天产煤多少万吨?
(0.16×3+0.195×4)÷(3+4)
比较:这4题有什么相同点,有什么不同点?
问题相同,条件不同
总重量÷天数=平均每天重量
(10×75+8×70)÷2
选择正确的算式:
①
勤工俭学小组包装茶叶,
第一组共有10人,平均每人包装茶叶75千克;
第二组共有8人,平均每人包装茶叶70千克。
1.平均每组包装茶叶多少千克?( )
2.平均每人包装茶叶多少千克?( )
(10×75+8×70)÷(10+8)
②
①
②
总千克数÷组数=平均每组千克数
总千克数÷人数=平均每人千克数
比较:这2题有什么相同点,有什么不同点?
条件相同,问题不同
选择正确的算式:
学校图书馆借书情况如下表:
月份 4 5 6 7 8 9
人数 28 31 32 0 0 29
4-9月平均每月借书的有多少人?( )
A.(28+31+32+29)÷4
B.(28+31+32+0+0+29)÷4
C.(29+32+32+0+0+30)÷6
C
在计算一组数据的平均数时,这组数据中的所有数(包括0)都要参加计算。
计算:
学校图书馆借书情况如下表:
月份 4 5 6 7 8 9
人数 28 31 32 0 0 29
4-9月平均每月借书的有多少人?
(29+32+32+0+0+30)÷6
=123÷6
=20.5(人)
(29+32+32+0+0+30)÷6
=30+(2+2-1)÷6
=30+3÷6
=30+0.5
=30.5(人)
在用平均数表示人数时,有时可能是小数。
=[30×4+(2+2-1)]÷6
=[120+3]÷6
=123÷6
=20.5(人)
平均数的认识
将一组数值的总和除以这组数值的个数,所得到的数叫做这组数值的平均数。
平均数
平均数的计算
平均数能较好地反映一组数据的总体情况,不代表个体。
平均数=总和÷个数
总和=平均数×个数
灵活合理
在用平均数表示人数时,有时可能是小数。
概念
特点
平均数处于这组数值的最大值和最小值之间。
方法
注意点
在计算一组数据的平均数时,这组数据中的所有数(包括0)都有参加计算。
总本数÷总人数=平均每人本数
√
?
(男生平均每人本数+女生平均每人本数)÷2=平均每人本数
√
B
(135.8×22+134.2×18)÷(22+18)
(135.7×20+134.3×20)÷(20+20)
(135.7+134.3)÷2
总身高÷总人数=全班的平均身高
总身高÷总人数=全班的平均身高
平均身高之和÷2=全班的平均身高
总路程÷总时间=全程的平均速度
(8×3+16×2)÷(3+2)
总路程÷总时间=全程的平均速度
(6×2+15×2)÷(2+2)
因为上山与下山时间相同
所以速度和÷2=平均速度
(6+15)÷2
平均数的认识
将一组数值的总和除以这组数值的个数,所得到的数叫做这组数值的平均数。
平均数
平均数的计算
平均数能较好地反映一组数据的总体情况,不代表个体。
平均数=总和÷个数
总和=平均数×个数
灵活合理
在用平均数表示人数时,有时可能是小数。
概念
特点
平均数处于这组数值的最大值和最小值之间。
方法
移多补少
注意点
在计算一组数据的平均数时,这组数据中的所有数(包括0)都有参加计算。
82×7+1-80×6
7×(82-80)=14(分)
=574+1-480
=575-480
=95(分)
80+14+1
=94 +1
=95(分)
法一:求和
法二:移多补少
平均数的认识
将一组数值的总和除以这组数值的个数,所得到的数叫做这组数值的平均数。
平均数
平均数的计算
平均数能较好地反映一组数据的总体情况,不代表个体。
平均数=总和÷个数
总和=平均数×个数
灵活合理
在用平均数表示人数时,有时可能是小数。
概念
特点
平均数处于这组数值的最大值和最小值之间。
方法
移多补少
注意点
在计算一组数据的平均数时,这组数据中的所有数(包括0)都有参加计算。
平均数的应用
选谁上场参加比赛?
“30秒颠球”比赛中,教练需要在甲乙两位队员中选出一人替补上场。
资料一:
因为15.4个>15个,
所以选乙队员上场。
资料二:两位队员训练成绩
稳定
小胖在操场上测了自己的步幅和步速,并整理成下面两个统计表。
小胖10步走的路程统计表
小胖1分钟走的路程统计表
走的 次数 1 2 3 4 5
10步走的路程(米) 4.9 4.8 4.7 4.7 4.9
走的 次数 1 2 3 4 5
1分钟走的步数 88 86 85 84 87
①小胖的平均步幅是多少米?
(4.9+4.8+4.7+4.7+4.9)÷5
÷10
②小胖平均每分钟可以走多少步?
③每分钟大约走多少米?
(88+86+85+84+87)÷5
平均步幅×平均步数=总距离
[(4.9+4.8+4.7+4.7+4.9)÷5
÷10]
×
[(88+86+85+84+87)÷5]
平均数的认识
将一组数值的总和除以这组数值的个数,所得到的数叫做这组数值的平均数。
平均数
平均数的计算
平均数能较好地反映一组数据的总体情况,不代表个体。
平均数=总和÷个数
总和=平均数×个数
灵活合理
在用平均数表示人数时,有时可能是小数。
平均数的应用
比较
推测
概念
特点
平均数处于这组数值的最大值和最小值之间。
方法
移多补少
注意点
在计算一组数据的平均数时,这组数据中的所有数(包括0)都有参加计算。
平均数
平均数的认识
将一组数值的总和除以这组数值的个数,所得到的数叫做这组数值的平均数。
平均数
概念
判断
(1)游泳池平均水深1.2米,小胖不会游泳,他身高1.45米,所以在游泳池中玩耍肯定安全。( )
(2)五(1)班学生平均身高155厘米,李强是其中最高的队员,他的身高是154厘米。( )
×
×
平均数能较好地反映一组数据的总体情况,不代表个体。
平均数处于这组数值的最大值和最小值之间。
平均数的认识
将一组数值的总和除以这组数值的个数,所得到的数叫做这组数值的平均数。
平均数
平均数能较好地反映一组数据的总体情况,不代表个体。
概念
特点
平均数处于这组数值的最大值和最小值之间。
平均数的计算
平均数=总和÷个数
方法
总和=平均数×个数
只列式,不计算。
1、某煤场7天产煤1.26万吨,平均每天产煤多少万吨?
1.26÷7
2、某煤场一周前3天产煤0.48万吨,后4天产煤0.78万吨,平均每天产煤多少万吨?
(0.48+0.78)÷(3+4)
3、某煤场一周前3天产煤0.48万吨,后4天每天产煤0.195万吨,平均每天产煤多少万吨?
(0.48+0.195×4)÷(3+4)
4、某煤场一周前3天每天产煤0.16万吨,后4天每天产煤0.195万吨,平均每天产煤多少万吨?
(0.16×3+0.195×4)÷(3+4)
比较:这4题有什么相同点,有什么不同点?
问题相同,条件不同
总重量÷天数=平均每天重量
(10×75+8×70)÷2
选择正确的算式:
①
勤工俭学小组包装茶叶,
第一组共有10人,平均每人包装茶叶75千克;
第二组共有8人,平均每人包装茶叶70千克。
1.平均每组包装茶叶多少千克?( )
2.平均每人包装茶叶多少千克?( )
(10×75+8×70)÷(10+8)
②
①
②
总千克数÷组数=平均每组千克数
总千克数÷人数=平均每人千克数
比较:这2题有什么相同点,有什么不同点?
条件相同,问题不同
选择正确的算式:
学校图书馆借书情况如下表:
月份 4 5 6 7 8 9
人数 28 31 32 0 0 29
4-9月平均每月借书的有多少人?( )
A.(28+31+32+29)÷4
B.(28+31+32+0+0+29)÷4
C.(29+32+32+0+0+30)÷6
C
在计算一组数据的平均数时,这组数据中的所有数(包括0)都要参加计算。
计算:
学校图书馆借书情况如下表:
月份 4 5 6 7 8 9
人数 28 31 32 0 0 29
4-9月平均每月借书的有多少人?
(29+32+32+0+0+30)÷6
=123÷6
=20.5(人)
(29+32+32+0+0+30)÷6
=30+(2+2-1)÷6
=30+3÷6
=30+0.5
=30.5(人)
在用平均数表示人数时,有时可能是小数。
=[30×4+(2+2-1)]÷6
=[120+3]÷6
=123÷6
=20.5(人)
平均数的认识
将一组数值的总和除以这组数值的个数,所得到的数叫做这组数值的平均数。
平均数
平均数的计算
平均数能较好地反映一组数据的总体情况,不代表个体。
平均数=总和÷个数
总和=平均数×个数
灵活合理
在用平均数表示人数时,有时可能是小数。
概念
特点
平均数处于这组数值的最大值和最小值之间。
方法
注意点
在计算一组数据的平均数时,这组数据中的所有数(包括0)都有参加计算。
总本数÷总人数=平均每人本数
√
?
(男生平均每人本数+女生平均每人本数)÷2=平均每人本数
√
B
(135.8×22+134.2×18)÷(22+18)
(135.7×20+134.3×20)÷(20+20)
(135.7+134.3)÷2
总身高÷总人数=全班的平均身高
总身高÷总人数=全班的平均身高
平均身高之和÷2=全班的平均身高
总路程÷总时间=全程的平均速度
(8×3+16×2)÷(3+2)
总路程÷总时间=全程的平均速度
(6×2+15×2)÷(2+2)
因为上山与下山时间相同
所以速度和÷2=平均速度
(6+15)÷2
平均数的认识
将一组数值的总和除以这组数值的个数,所得到的数叫做这组数值的平均数。
平均数
平均数的计算
平均数能较好地反映一组数据的总体情况,不代表个体。
平均数=总和÷个数
总和=平均数×个数
灵活合理
在用平均数表示人数时,有时可能是小数。
概念
特点
平均数处于这组数值的最大值和最小值之间。
方法
移多补少
注意点
在计算一组数据的平均数时,这组数据中的所有数(包括0)都有参加计算。
82×7+1-80×6
7×(82-80)=14(分)
=574+1-480
=575-480
=95(分)
80+14+1
=94 +1
=95(分)
法一:求和
法二:移多补少
平均数的认识
将一组数值的总和除以这组数值的个数,所得到的数叫做这组数值的平均数。
平均数
平均数的计算
平均数能较好地反映一组数据的总体情况,不代表个体。
平均数=总和÷个数
总和=平均数×个数
灵活合理
在用平均数表示人数时,有时可能是小数。
概念
特点
平均数处于这组数值的最大值和最小值之间。
方法
移多补少
注意点
在计算一组数据的平均数时,这组数据中的所有数(包括0)都有参加计算。
平均数的应用
选谁上场参加比赛?
“30秒颠球”比赛中,教练需要在甲乙两位队员中选出一人替补上场。
资料一:
因为15.4个>15个,
所以选乙队员上场。
资料二:两位队员训练成绩
稳定
小胖在操场上测了自己的步幅和步速,并整理成下面两个统计表。
小胖10步走的路程统计表
小胖1分钟走的路程统计表
走的 次数 1 2 3 4 5
10步走的路程(米) 4.9 4.8 4.7 4.7 4.9
走的 次数 1 2 3 4 5
1分钟走的步数 88 86 85 84 87
①小胖的平均步幅是多少米?
(4.9+4.8+4.7+4.7+4.9)÷5
÷10
②小胖平均每分钟可以走多少步?
③每分钟大约走多少米?
(88+86+85+84+87)÷5
平均步幅×平均步数=总距离
[(4.9+4.8+4.7+4.7+4.9)÷5
÷10]
×
[(88+86+85+84+87)÷5]
平均数的认识
将一组数值的总和除以这组数值的个数,所得到的数叫做这组数值的平均数。
平均数
平均数的计算
平均数能较好地反映一组数据的总体情况,不代表个体。
平均数=总和÷个数
总和=平均数×个数
灵活合理
在用平均数表示人数时,有时可能是小数。
平均数的应用
比较
推测
概念
特点
平均数处于这组数值的最大值和最小值之间。
方法
移多补少
注意点
在计算一组数据的平均数时,这组数据中的所有数(包括0)都有参加计算。
同课章节目录
