12.2三角形全等的判定 同步练习 2023-2024学年人教版数学八年级上册(含答案)
文档属性
| 名称 | 12.2三角形全等的判定 同步练习 2023-2024学年人教版数学八年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 542.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-12 18:02:02 | ||
图片预览

文档简介
12.2三角形全等的判定 同步练习
一、单选题
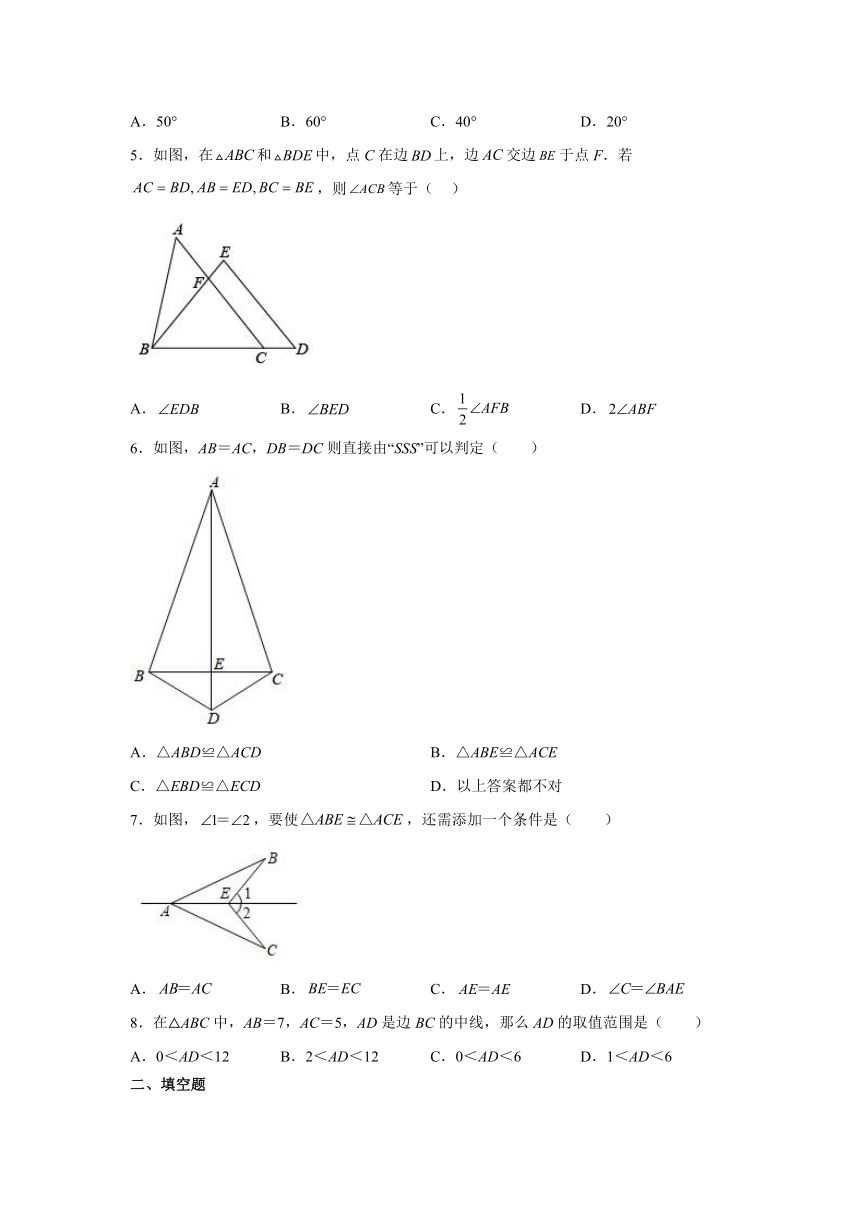
1.已知是的边上一点,交于点,,,若,,则的长为( )
A.1 B.3 C.5 D.7
2.如图,在中,,D是上一点,于点E,,连接,若,则等于( )
A.6 B.7 C.8 D.9
3.已知如图,要测量水池的宽AB,可过点A作直线AC⊥AB,再由点C观测,在BA延长线上找一点,使,这时只要出的长,就知道AB的长,那么判定≌的理由是( )
A.ASA B.AAS C.SAS D.HL
4.如图,在△ABC中,D,E是BC边上的两点,AD=AE,BE=CD,∠1=∠2=110°,∠BAE=60°,则∠CAE的度数为( )
A.50° B.60° C.40° D.20°
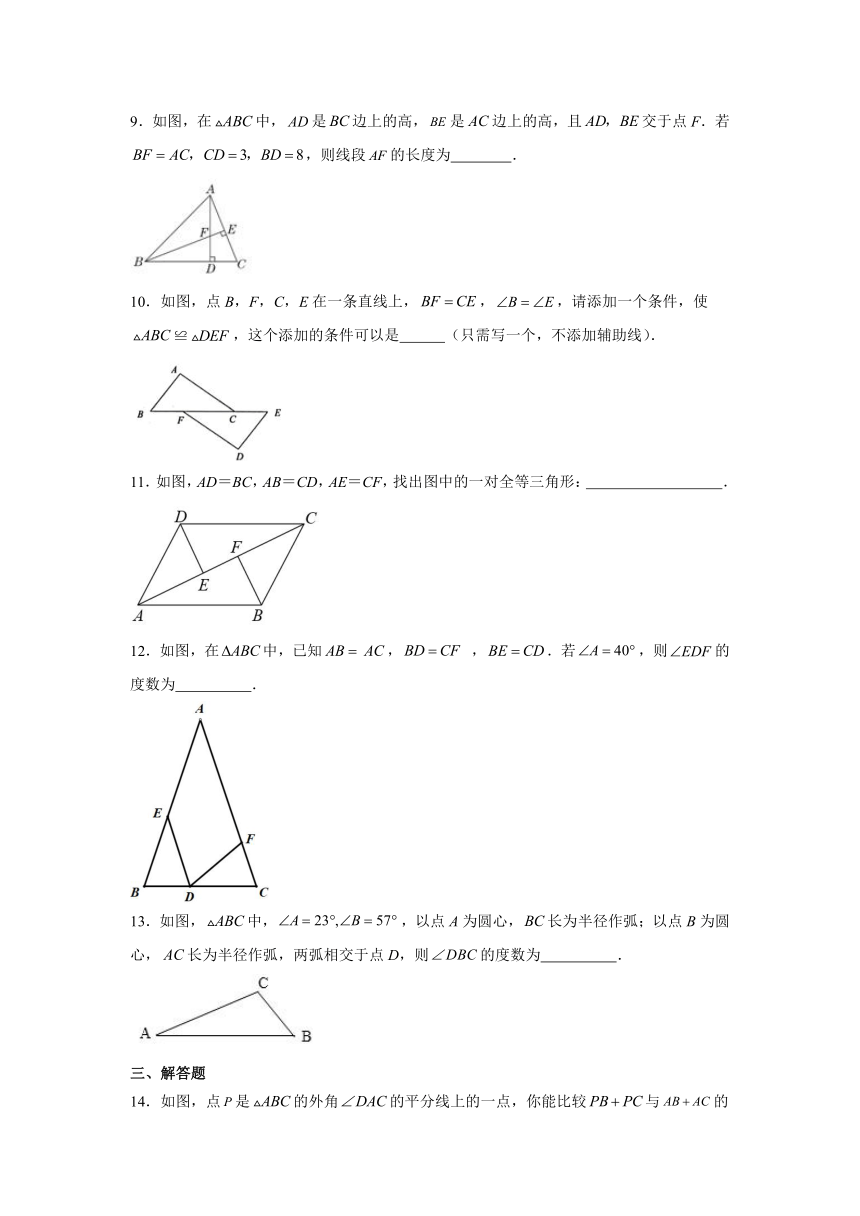
5.如图,在和中,点C在边上,边交边于点F.若,则等于( )
A. B. C. D.
6.如图,AB=AC,DB=DC则直接由“SSS”可以判定( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△EBD≌△ECD D.以上答案都不对
7.如图,,要使,还需添加一个条件是( )
A. B. C. D.
8.在△ABC中,AB=7,AC=5,AD是边BC的中线,那么AD的取值范围是( )
A.0<AD<12 B.2<AD<12 C.0<AD<6 D.1<AD<6
二、填空题
9.如图,在中,是边上的高,是边上的高,且交于点F.若,则线段的长度为 .
10.如图,点B,F,C,E在一条直线上,,,请添加一个条件,使≌,这个添加的条件可以是 (只需写一个,不添加辅助线).
11.如图,AD=BC,AB=CD,AE=CF,找出图中的一对全等三角形: .
12.如图,在中,已知, ,.若,则的度数为 .
13.如图,中,,以点A为圆心,长为半径作弧;以点B为圆心,长为半径作弧,两弧相交于点D,则的度数为 .
三、解答题
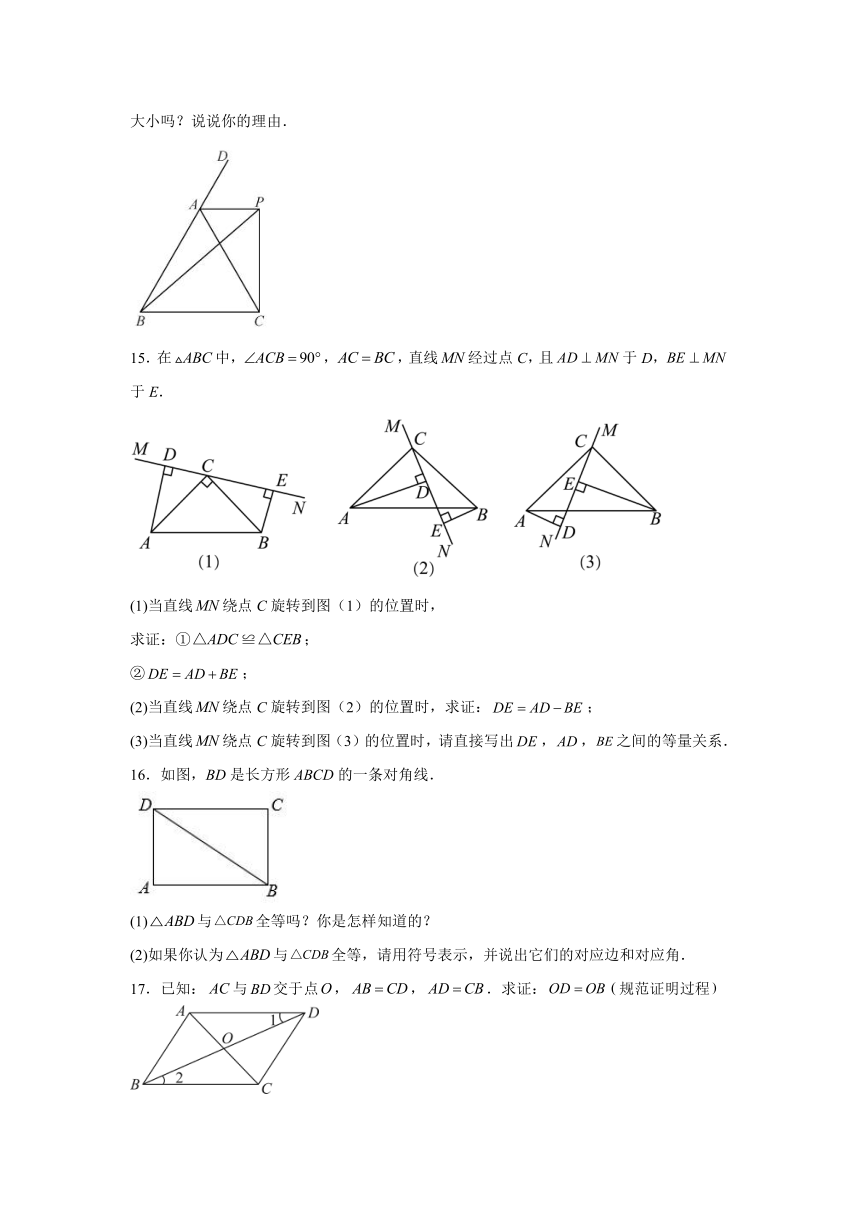
14.如图,点是的外角的平分线上的一点,你能比较与的大小吗?说说你的理由.
15.在中,,,直线经过点C,且于D,于E.
(1)当直线绕点C旋转到图(1)的位置时,
求证:①;
②;
(2)当直线绕点C旋转到图(2)的位置时,求证:;
(3)当直线绕点C旋转到图(3)的位置时,请直接写出,,之间的等量关系.
16.如图,BD是长方形ABCD的一条对角线.
(1)与全等吗?你是怎样知道的?
(2)如果你认为与全等,请用符号表示,并说出它们的对应边和对应角.
17.已知:与交于点,,.求证:规范证明过程
证明:在和中,
______
______ ______
在和中,
______
.
参考答案
1--8DCADC ABD
9.5
10.(还可以添加∠A=∠D或∠ACB=∠EFD或AC∥DF,答案不唯一)
11.或或.
12.70°
13.34°或80°
14.解:,理由如下:
如图所示,在射线上取一点,使,连接.
平分,
.
又,
,
.
在中,,
.
15.(1)①∵,,
∴,
∴,,
∴,
在和中,
,
∴;
②∵,
∴,,
∴;
(2)证明:∵,,
∴,
∴,
在和中,
,
∴;
∴,,
∴;
(3)当MN旋转到题图(3)的位置时,,,所满足的等量关系是:.
理由如下:∵,,
∴,
∴,
在和中,
,
∴;
∴,,
∴.
16.(1)解:与全等,理由如下:
∵BD是长方形ABCD的一条对角线,
∴,
∴,
在与中,
∵,
∴;
(2)解: 与全等,用符号表示:;
对应边:,
对应角:.
17.证明:在和中,
在和中,
.
故答案为:,,,,1,2,,,,.
一、单选题
1.已知是的边上一点,交于点,,,若,,则的长为( )
A.1 B.3 C.5 D.7
2.如图,在中,,D是上一点,于点E,,连接,若,则等于( )
A.6 B.7 C.8 D.9
3.已知如图,要测量水池的宽AB,可过点A作直线AC⊥AB,再由点C观测,在BA延长线上找一点,使,这时只要出的长,就知道AB的长,那么判定≌的理由是( )
A.ASA B.AAS C.SAS D.HL
4.如图,在△ABC中,D,E是BC边上的两点,AD=AE,BE=CD,∠1=∠2=110°,∠BAE=60°,则∠CAE的度数为( )
A.50° B.60° C.40° D.20°
5.如图,在和中,点C在边上,边交边于点F.若,则等于( )
A. B. C. D.
6.如图,AB=AC,DB=DC则直接由“SSS”可以判定( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△EBD≌△ECD D.以上答案都不对
7.如图,,要使,还需添加一个条件是( )
A. B. C. D.
8.在△ABC中,AB=7,AC=5,AD是边BC的中线,那么AD的取值范围是( )
A.0<AD<12 B.2<AD<12 C.0<AD<6 D.1<AD<6
二、填空题
9.如图,在中,是边上的高,是边上的高,且交于点F.若,则线段的长度为 .
10.如图,点B,F,C,E在一条直线上,,,请添加一个条件,使≌,这个添加的条件可以是 (只需写一个,不添加辅助线).
11.如图,AD=BC,AB=CD,AE=CF,找出图中的一对全等三角形: .
12.如图,在中,已知, ,.若,则的度数为 .
13.如图,中,,以点A为圆心,长为半径作弧;以点B为圆心,长为半径作弧,两弧相交于点D,则的度数为 .
三、解答题
14.如图,点是的外角的平分线上的一点,你能比较与的大小吗?说说你的理由.
15.在中,,,直线经过点C,且于D,于E.
(1)当直线绕点C旋转到图(1)的位置时,
求证:①;
②;
(2)当直线绕点C旋转到图(2)的位置时,求证:;
(3)当直线绕点C旋转到图(3)的位置时,请直接写出,,之间的等量关系.
16.如图,BD是长方形ABCD的一条对角线.
(1)与全等吗?你是怎样知道的?
(2)如果你认为与全等,请用符号表示,并说出它们的对应边和对应角.
17.已知:与交于点,,.求证:规范证明过程
证明:在和中,
______
______ ______
在和中,
______
.
参考答案
1--8DCADC ABD
9.5
10.(还可以添加∠A=∠D或∠ACB=∠EFD或AC∥DF,答案不唯一)
11.或或.
12.70°
13.34°或80°
14.解:,理由如下:
如图所示,在射线上取一点,使,连接.
平分,
.
又,
,
.
在中,,
.
15.(1)①∵,,
∴,
∴,,
∴,
在和中,
,
∴;
②∵,
∴,,
∴;
(2)证明:∵,,
∴,
∴,
在和中,
,
∴;
∴,,
∴;
(3)当MN旋转到题图(3)的位置时,,,所满足的等量关系是:.
理由如下:∵,,
∴,
∴,
在和中,
,
∴;
∴,,
∴.
16.(1)解:与全等,理由如下:
∵BD是长方形ABCD的一条对角线,
∴,
∴,
在与中,
∵,
∴;
(2)解: 与全等,用符号表示:;
对应边:,
对应角:.
17.证明:在和中,
在和中,
.
故答案为:,,,,1,2,,,,.
