组合图形面积计算表格式教案沪教版三年级下册数学
文档属性
| 名称 | 组合图形面积计算表格式教案沪教版三年级下册数学 |
|
|
| 格式 | docx | ||
| 文件大小 | 32.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-12 00:00:00 | ||
图片预览

文档简介
上课日期:
课题 组合图形面积计算2(练习课) 课型 练习 课时 1
教 学 目 标 1、能够正确运用分割法将组合图形转化成已学过的长方形、正方形,然后计算出原组合图形的面积。 2、能够运用补形法将组合图形转化成已学过的长方形、正方形,然后计算出原组合图形的面积。 3、初步学会转化思想。
教学重点 正确、合理选择不同的方法解决组合图形的面积。
教学难点 正确、合理选择不同的方法解决组合图形的面积。
教法与学法 尝试交流
教 学 过 程
教师活动设计 学生活动设计
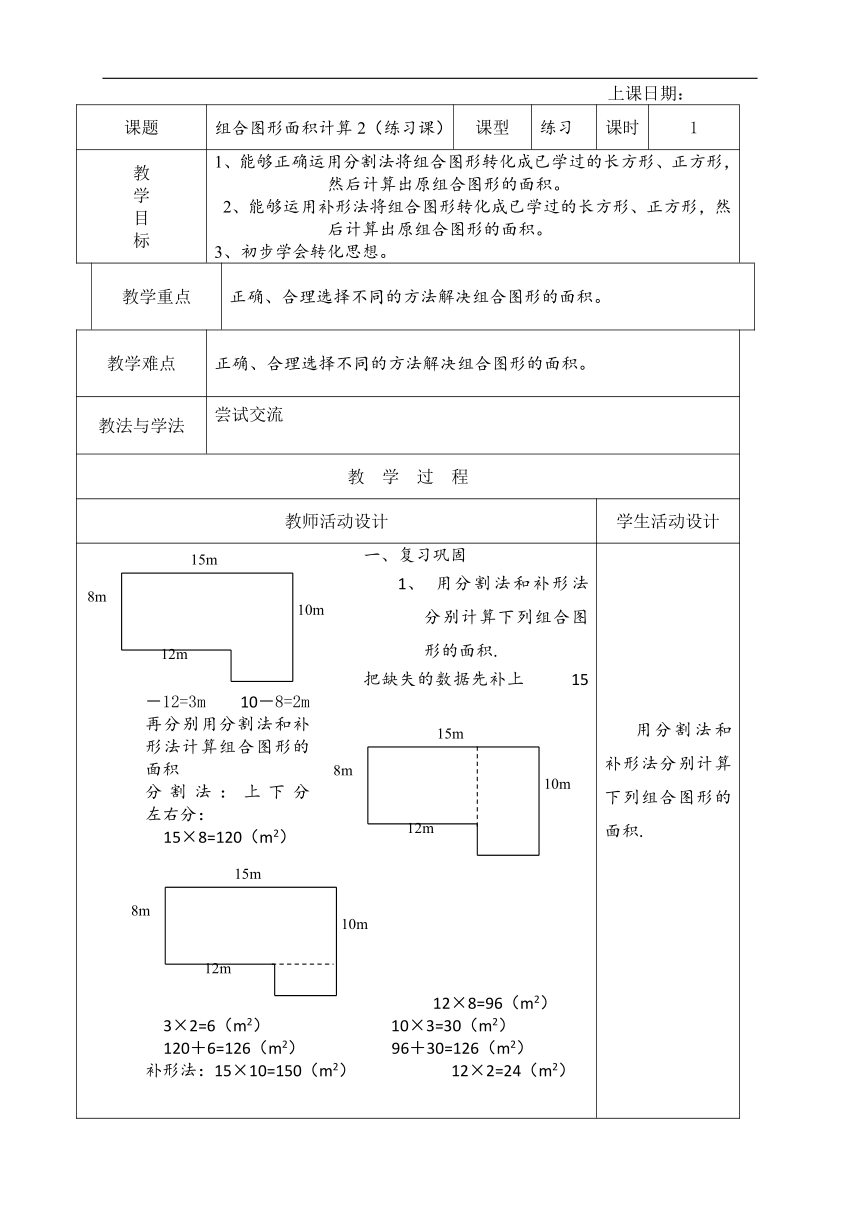
一、复习巩固 (
8m
12m
15m
10m
)用分割法和补形法分别计算下列组合图形的面积. (
8m
12m
15m
10m
)把缺失的数据先补上 15-12=3m 10-8=2m 再分别用分割法和补形法计算组合图形的面积 分割法:上下分 左右分: 15×8=120(m2) (
8m
12m
15m
10m
) 12×8=96(m2) 3×2=6(m2) 10×3=30(m2) 120+6=126(m2) 96+30=126(m2) 补形法:15×10=150(m2) 12×2=24(m2) (
8m
12m
15m
10m
) 150-24=126(m2) 计算下列组合图形的面积。 注意按照上面总结出来的步骤进行。 (
10m
6m
2m
2m
3m
) 10-2-3=5(m) 6-2=4(m) (1)10×6-5×2=50(m2) (2)6×2+6×3+5×4=50(m2) 3、小结:计算组合图形面积的步骤是怎样的?计算的方法又是怎样的? (
2cm
3cm
2cm
2cm
8cm
)二、学生巩固练习。 (
8cm
8cm
3cm
3cm
) 1、求下列涂色部分图形的面积。 8-2-3=3(m) (1)2×2+8×2=20(m2) 8×8-3×3=55(cm2) (2)3×2×2+4×2=20(m2) (
10m
10m
1m
1m
) 10-1=9(m) 100×1=100(m2) 10 ×1=10(m2) 9 ×1=9(m2) 100-10-9=81(m2) (
1m
10m
10m
1m
) 介绍平移法: 10-1=9(m) 9×9=81(m2) 三、课堂小结: 解决组合图形大小的步骤是怎样的? 你学会了几种解题方法? 四、回家作业 书上P7/练一练5题。 用分割法和补形法分别计算下列组合图形的面积. 按照上面总结出来的步骤进行 巩固练习 拓展练习 学生课堂小结 练一练5题
课后反思:
课题 组合图形面积计算2(练习课) 课型 练习 课时 1
教 学 目 标 1、能够正确运用分割法将组合图形转化成已学过的长方形、正方形,然后计算出原组合图形的面积。 2、能够运用补形法将组合图形转化成已学过的长方形、正方形,然后计算出原组合图形的面积。 3、初步学会转化思想。
教学重点 正确、合理选择不同的方法解决组合图形的面积。
教学难点 正确、合理选择不同的方法解决组合图形的面积。
教法与学法 尝试交流
教 学 过 程
教师活动设计 学生活动设计
一、复习巩固 (
8m
12m
15m
10m
)用分割法和补形法分别计算下列组合图形的面积. (
8m
12m
15m
10m
)把缺失的数据先补上 15-12=3m 10-8=2m 再分别用分割法和补形法计算组合图形的面积 分割法:上下分 左右分: 15×8=120(m2) (
8m
12m
15m
10m
) 12×8=96(m2) 3×2=6(m2) 10×3=30(m2) 120+6=126(m2) 96+30=126(m2) 补形法:15×10=150(m2) 12×2=24(m2) (
8m
12m
15m
10m
) 150-24=126(m2) 计算下列组合图形的面积。 注意按照上面总结出来的步骤进行。 (
10m
6m
2m
2m
3m
) 10-2-3=5(m) 6-2=4(m) (1)10×6-5×2=50(m2) (2)6×2+6×3+5×4=50(m2) 3、小结:计算组合图形面积的步骤是怎样的?计算的方法又是怎样的? (
2cm
3cm
2cm
2cm
8cm
)二、学生巩固练习。 (
8cm
8cm
3cm
3cm
) 1、求下列涂色部分图形的面积。 8-2-3=3(m) (1)2×2+8×2=20(m2) 8×8-3×3=55(cm2) (2)3×2×2+4×2=20(m2) (
10m
10m
1m
1m
) 10-1=9(m) 100×1=100(m2) 10 ×1=10(m2) 9 ×1=9(m2) 100-10-9=81(m2) (
1m
10m
10m
1m
) 介绍平移法: 10-1=9(m) 9×9=81(m2) 三、课堂小结: 解决组合图形大小的步骤是怎样的? 你学会了几种解题方法? 四、回家作业 书上P7/练一练5题。 用分割法和补形法分别计算下列组合图形的面积. 按照上面总结出来的步骤进行 巩固练习 拓展练习 学生课堂小结 练一练5题
课后反思:
