等比数列前n项和(第一课时)[上学期]
文档属性
| 名称 | 等比数列前n项和(第一课时)[上学期] |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-21 17:11:00 | ||
图片预览





文档简介
(共18张PPT)
等比数列前n项和
奎屯市第一高级中学 刘杰
$啊!!
自从猪八戒成立“高老庄”集团以来,第一次遇到了资金运转问题。
高老庄集团
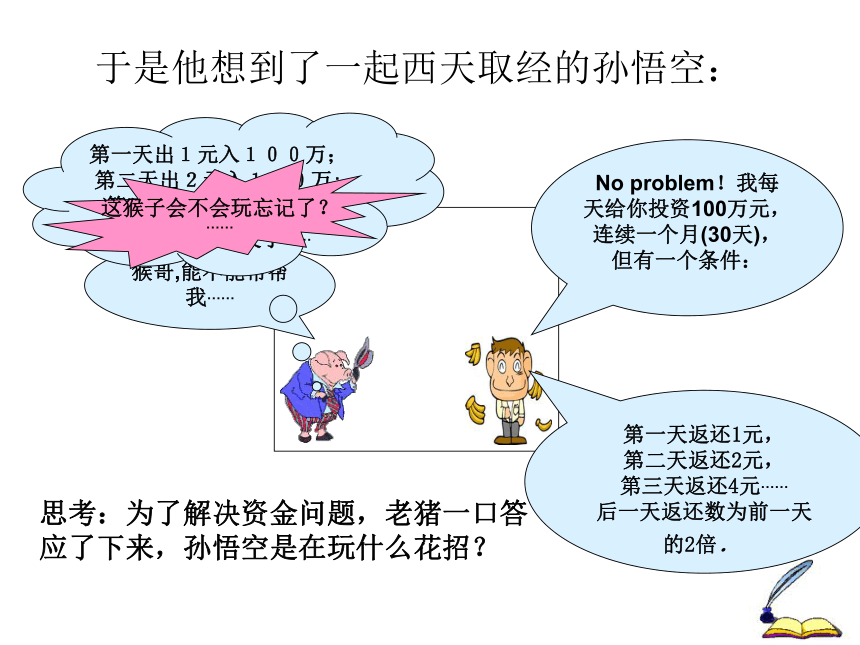
于是他想到了一起西天取经的孙悟空:
No problem!我每天给你投资100万元, 连续一个月(30天),但有一个条件:
猴哥,能不能帮帮我……
第一天返还1元,
第二天返还2元,
第三天返还4元……
后一天返还数为前一天的2倍.
第一天出1元入100万;第二天出2元入100万;第三天出4元入100万元;……哇,发了……
这猴子会不会玩忘记了?
……
思考:为了解决资金问题,老猪一口答应了下来,孙悟空是在玩什么花招?
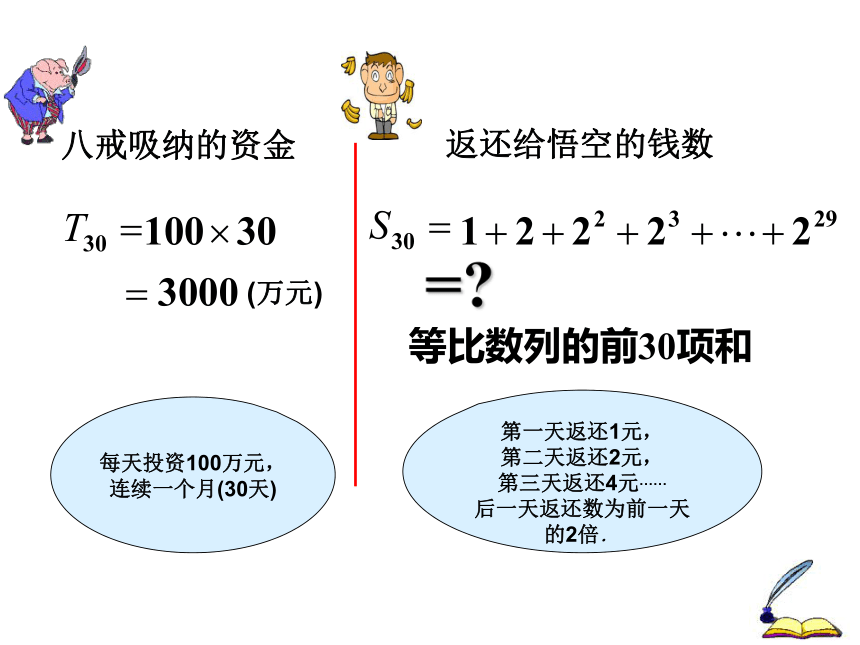
八戒吸纳的资金
返还给悟空的钱数
(万元)
等比数列的前30项和
每天投资100万元,连续一个月(30天)
第一天返还1元,
第二天返还2元,
第三天返还4元……
后一天返还数为前一天的2倍.
=
在等比数列中,我们知道:从第二项起,它的前一项乘以公比等于后一项
上述问题:求以首项为1,公比为2的等比数列的前30项的和
两边同乘公比2,得
现在我们将上面两式放在一起,进行比较:
② - ①,得
①
②
聪明的你发现了什么
?
?
八戒拿到赞助,高兴的去告诉高小姐!
八戒如实告诉…
高小姐会心一算…
你个猪啊!
要还107374万啊!
等比数列的前n项和
归纳:首项为 ,公比为 的等比数列 的前n项的和吗?
q
-
1
当q≠1时,
当q=1时,
我们把这种方法叫做:错位相减法
q
-
1
当q≠1时,
当q=1时,
错位相减法推导:
我们把 带入上式就可以得到:
这样我们得到:首项为 ,公比为 的等比数列 的前n项的和的两个公式:
等比数列的前n项和
如果我们知道了一个等比数列的首项与公比(或也知道末项),就可以求出任意前n项的和。
例如:
?
分析:首项为1,公比为2,末项为 。
运用第一个公式: 运用第二个公式:
怎么回事?它共有n+1项,原来如此!
n+1
n+1
n+1
解:
原式
例1:求等比数列 的前8项的和。
分析:在这个等比数列中,首项 ,公比 ,要求的是
解:由 得:
对了吗
?
应该是 而不是 , 是一个公式。而 是一个具体的值。
8
分析:先要知道n是多少?由首项,公比与 ,求出n,再利用公式。
解:
例2:在等比数列中已知 , , ,求 , ?
例3:在等比数列中已知 , , ,求 与 n ?
解:由题意可知
归纳:在等比数列中, , , , , 这五个量中。
知三求二
课堂练习:人教版P128课本练习1,2。
答案:1~(1): ~(2):
~(3): ~(4):
2~(1): ~(2):
【解法1】
此等比数列的第5项到第10项构成一个
首项是
【解法2】
的等比数列
公比为
,项数
练习 求等比数列 的第5项到第10项的和.
例4:某商场第1年销售计算机5000台,如果平均每年的销售量比上一年增加10%。那么从第1年起,约几年内可使总销售量达到30 0000台(保留到个位)
分析:第1年: ,第2年: …第n年:
解: 根据题意,每年销售量比上一年增加的百分率相同,所以从第1年起,每年的销售量组成一个等比数列 ,其中:
于是得到
整理后,得
两边取常用对数,得
用计算器可得
(年)
注意
答:约5年内可以使总销售量达到30 0000台!
小结:今天我们讲的内容是等比数列的前n项求和。
一、首先它的公式有两个:
二、它的推导方法:
错位相减法;
三、在等比数列中, , , , , 这五个量中。
知三求二
四、等比数列在实际生活中的应用。(注意:1~设数列;2~答)
n
注意:n
布置作业:今天的课后作业是
一、课本(人教版)P129~习题3.5
第1题,第2题,第3题(要求:要抄题;做题要规范)
二、复习今天的内容并预习下节课的内容。
三、课后思考题:
(提示:错位相减法)
求数列 1, , ,…, ,…的
前4项的和,并归纳其前n项的和公式。
思考:是否还有其他方法求等比数列前n项和呢?
这里我们还介绍另外两种求等比数列前n项和的方法:
第二种:提取公比法
当q≠1时,
当q=1时,
第三种:等比定理法( )
即
当q≠1时,
当q=1时,
条条大路通罗马
事事多动小脑筋
天下无难事
= = 我!
等比数列前n项和
奎屯市第一高级中学 刘杰
$啊!!
自从猪八戒成立“高老庄”集团以来,第一次遇到了资金运转问题。
高老庄集团
于是他想到了一起西天取经的孙悟空:
No problem!我每天给你投资100万元, 连续一个月(30天),但有一个条件:
猴哥,能不能帮帮我……
第一天返还1元,
第二天返还2元,
第三天返还4元……
后一天返还数为前一天的2倍.
第一天出1元入100万;第二天出2元入100万;第三天出4元入100万元;……哇,发了……
这猴子会不会玩忘记了?
……
思考:为了解决资金问题,老猪一口答应了下来,孙悟空是在玩什么花招?
八戒吸纳的资金
返还给悟空的钱数
(万元)
等比数列的前30项和
每天投资100万元,连续一个月(30天)
第一天返还1元,
第二天返还2元,
第三天返还4元……
后一天返还数为前一天的2倍.
=
在等比数列中,我们知道:从第二项起,它的前一项乘以公比等于后一项
上述问题:求以首项为1,公比为2的等比数列的前30项的和
两边同乘公比2,得
现在我们将上面两式放在一起,进行比较:
② - ①,得
①
②
聪明的你发现了什么
?
?
八戒拿到赞助,高兴的去告诉高小姐!
八戒如实告诉…
高小姐会心一算…
你个猪啊!
要还107374万啊!
等比数列的前n项和
归纳:首项为 ,公比为 的等比数列 的前n项的和吗?
q
-
1
当q≠1时,
当q=1时,
我们把这种方法叫做:错位相减法
q
-
1
当q≠1时,
当q=1时,
错位相减法推导:
我们把 带入上式就可以得到:
这样我们得到:首项为 ,公比为 的等比数列 的前n项的和的两个公式:
等比数列的前n项和
如果我们知道了一个等比数列的首项与公比(或也知道末项),就可以求出任意前n项的和。
例如:
?
分析:首项为1,公比为2,末项为 。
运用第一个公式: 运用第二个公式:
怎么回事?它共有n+1项,原来如此!
n+1
n+1
n+1
解:
原式
例1:求等比数列 的前8项的和。
分析:在这个等比数列中,首项 ,公比 ,要求的是
解:由 得:
对了吗
?
应该是 而不是 , 是一个公式。而 是一个具体的值。
8
分析:先要知道n是多少?由首项,公比与 ,求出n,再利用公式。
解:
例2:在等比数列中已知 , , ,求 , ?
例3:在等比数列中已知 , , ,求 与 n ?
解:由题意可知
归纳:在等比数列中, , , , , 这五个量中。
知三求二
课堂练习:人教版P128课本练习1,2。
答案:1~(1): ~(2):
~(3): ~(4):
2~(1): ~(2):
【解法1】
此等比数列的第5项到第10项构成一个
首项是
【解法2】
的等比数列
公比为
,项数
练习 求等比数列 的第5项到第10项的和.
例4:某商场第1年销售计算机5000台,如果平均每年的销售量比上一年增加10%。那么从第1年起,约几年内可使总销售量达到30 0000台(保留到个位)
分析:第1年: ,第2年: …第n年:
解: 根据题意,每年销售量比上一年增加的百分率相同,所以从第1年起,每年的销售量组成一个等比数列 ,其中:
于是得到
整理后,得
两边取常用对数,得
用计算器可得
(年)
注意
答:约5年内可以使总销售量达到30 0000台!
小结:今天我们讲的内容是等比数列的前n项求和。
一、首先它的公式有两个:
二、它的推导方法:
错位相减法;
三、在等比数列中, , , , , 这五个量中。
知三求二
四、等比数列在实际生活中的应用。(注意:1~设数列;2~答)
n
注意:n
布置作业:今天的课后作业是
一、课本(人教版)P129~习题3.5
第1题,第2题,第3题(要求:要抄题;做题要规范)
二、复习今天的内容并预习下节课的内容。
三、课后思考题:
(提示:错位相减法)
求数列 1, , ,…, ,…的
前4项的和,并归纳其前n项的和公式。
思考:是否还有其他方法求等比数列前n项和呢?
这里我们还介绍另外两种求等比数列前n项和的方法:
第二种:提取公比法
当q≠1时,
当q=1时,
第三种:等比定理法( )
即
当q≠1时,
当q=1时,
条条大路通罗马
事事多动小脑筋
天下无难事
= = 我!
