2023-2024学年苏科版九年级数学上册 2.2圆的对称性 同步练习题(含解析)
文档属性
| 名称 | 2023-2024学年苏科版九年级数学上册 2.2圆的对称性 同步练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 322.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-13 00:00:00 | ||
图片预览

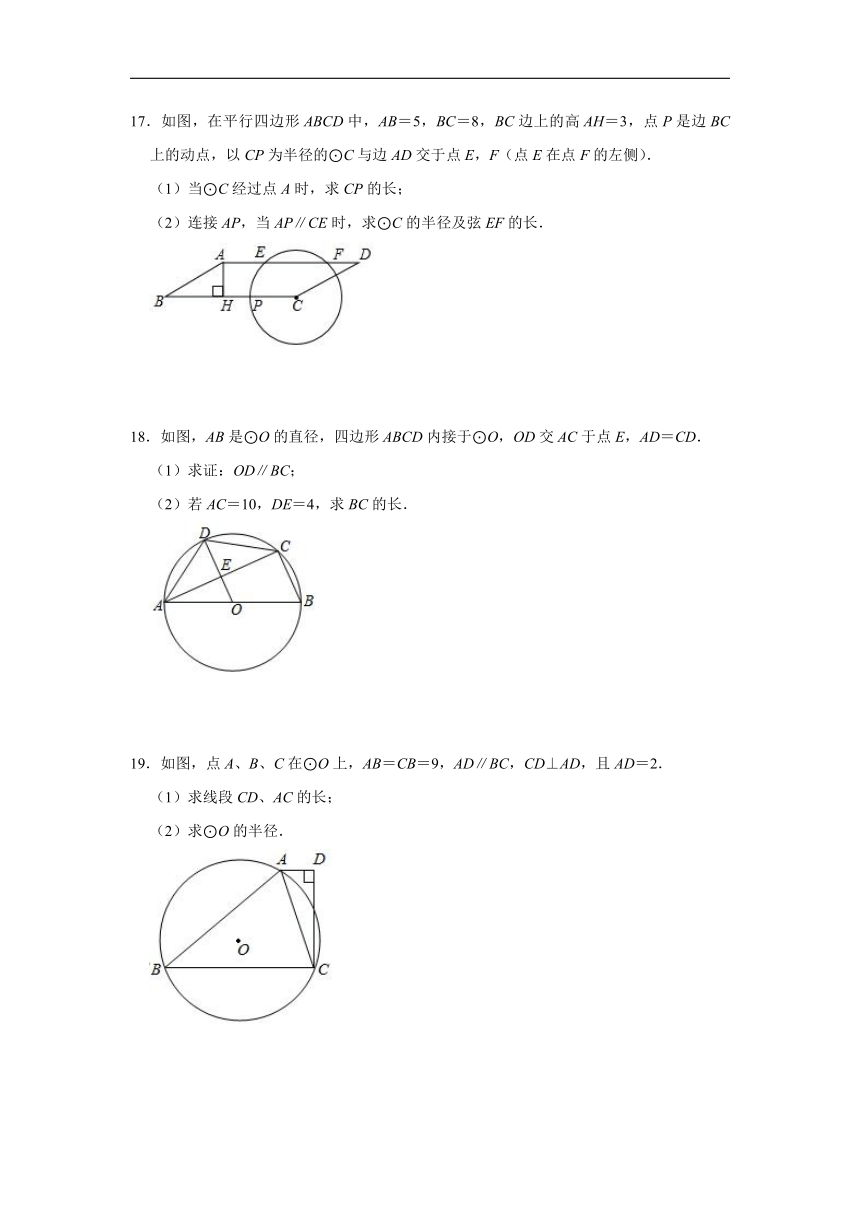
文档简介
2023-2024学年苏科版九年级数学上册《2.2圆的对称性》同步练习题(附答案)
一.选择题
1.⊙O的半径为5,M是圆外一点,MO=6,∠OMA=30°,则弦AB的长为( )
A.4 B.6 C.6 D.8
2.如图,在⊙O中将弧AB沿弦AB翻折经过圆心O交弦BE于点F,BF=2EF,AB=2,则BE长为( )
A.4 B.3 C.3 D.6
3.如图,AB为⊙O的直径,点C、D是的三等分点,∠AOE=60°,则∠BOD的度数为( )
A.40° B.60° C.80° D.120°
4.如图,是某供水管道的截面图,里面尚有一些水,若液面宽度AB=8cm,半径OC⊥AB于D,液面深度CD=2cm,则该管道的半径长为( )
A.6cm B.5.5cm C.5cm D.4cm
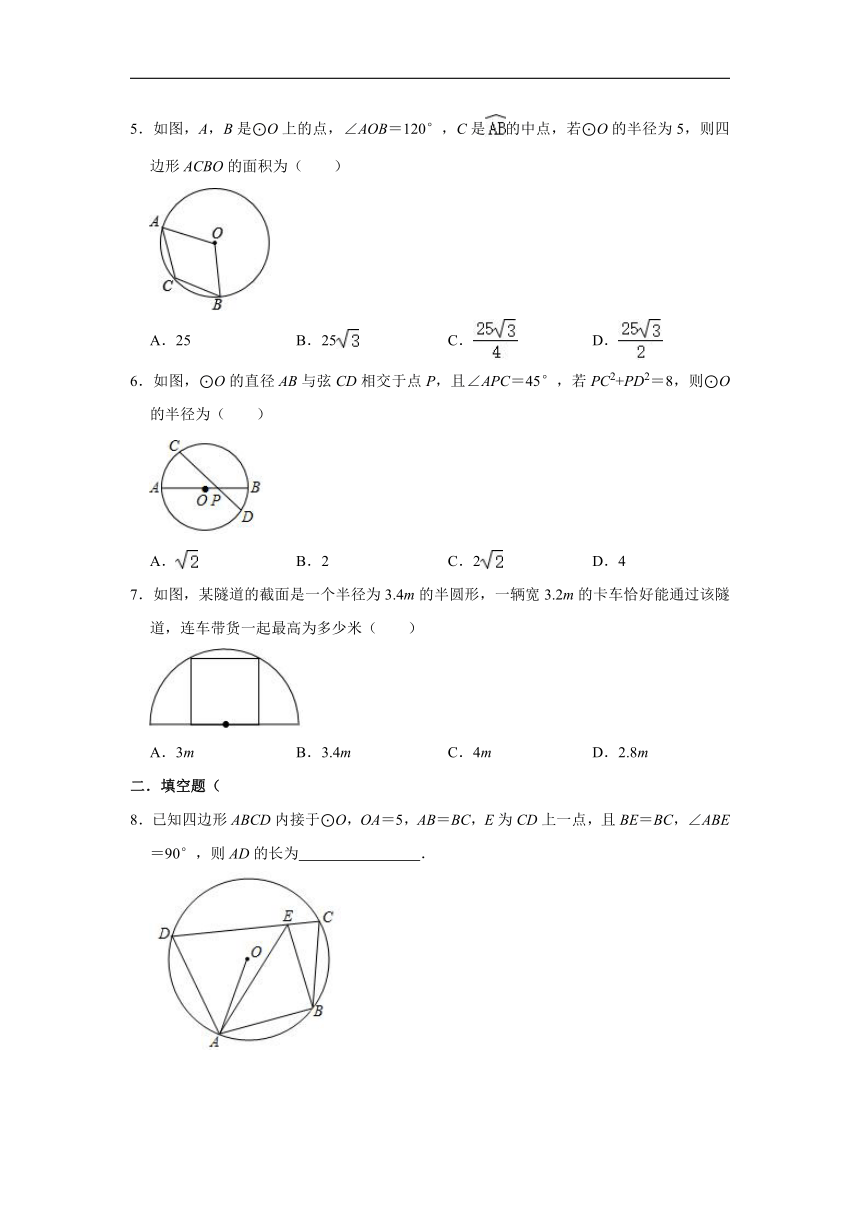
5.如图,A,B是⊙O上的点,∠AOB=120°,C是的中点,若⊙O的半径为5,则四边形ACBO的面积为( )
A.25 B.25 C. D.
6.如图,⊙O的直径AB与弦CD相交于点P,且∠APC=45°,若PC2+PD2=8,则⊙O的半径为( )
A. B.2 C.2 D.4
7.如图,某隧道的截面是一个半径为3.4m的半圆形,一辆宽3.2m的卡车恰好能通过该隧道,连车带货一起最高为多少米( )
A.3m B.3.4m C.4m D.2.8m
二.填空题(
8.已知四边形ABCD内接于⊙O,OA=5,AB=BC,E为CD上一点,且BE=BC,∠ABE=90°,则AD的长为 .
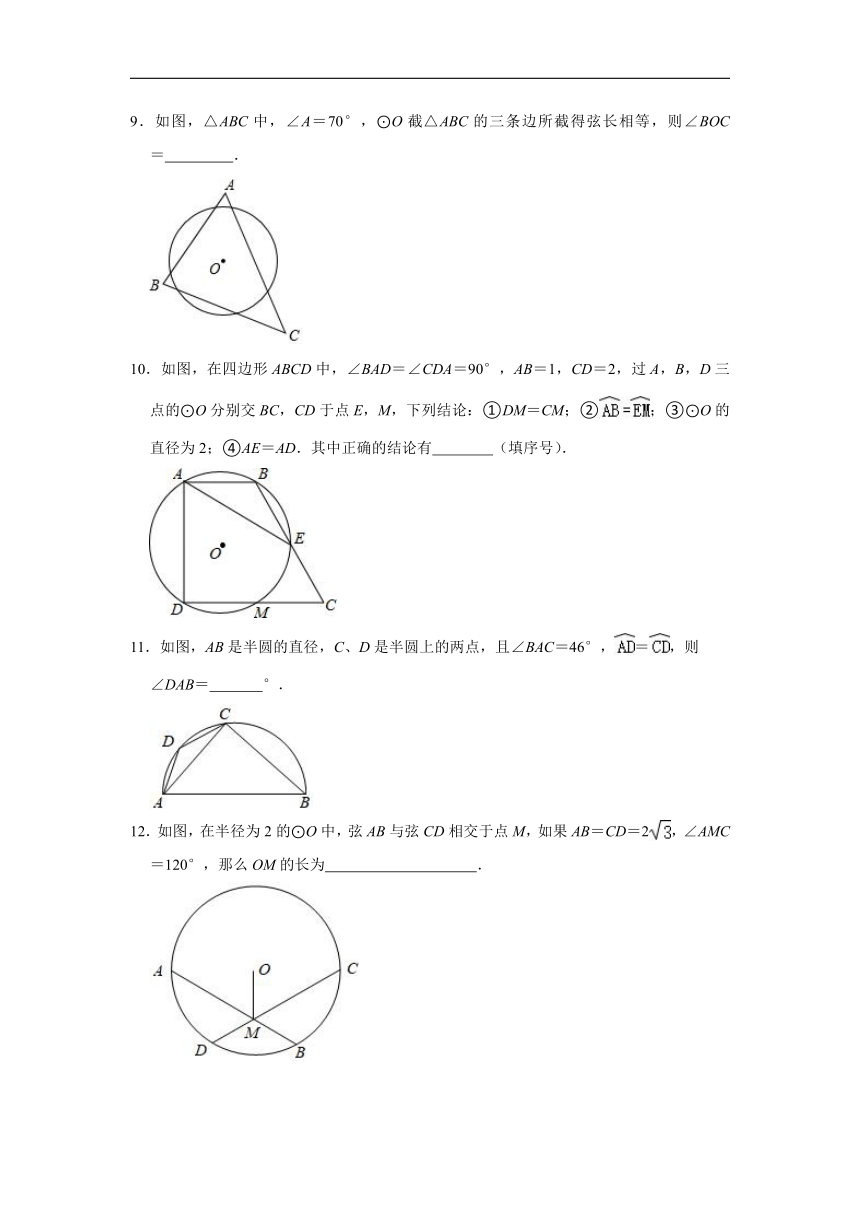
9.如图,△ABC中,∠A=70°,⊙O截△ABC的三条边所截得弦长相等,则∠BOC= .
10.如图,在四边形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,过A,B,D三点的⊙O分别交BC,CD于点E,M,下列结论:①DM=CM;②;③⊙O的直径为2;④AE=AD.其中正确的结论有 (填序号).
11.如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=46°,=,则
∠DAB= °.
12.如图,在半径为2的⊙O中,弦AB与弦CD相交于点M,如果AB=CD=2,∠AMC=120°,那么OM的长为 .
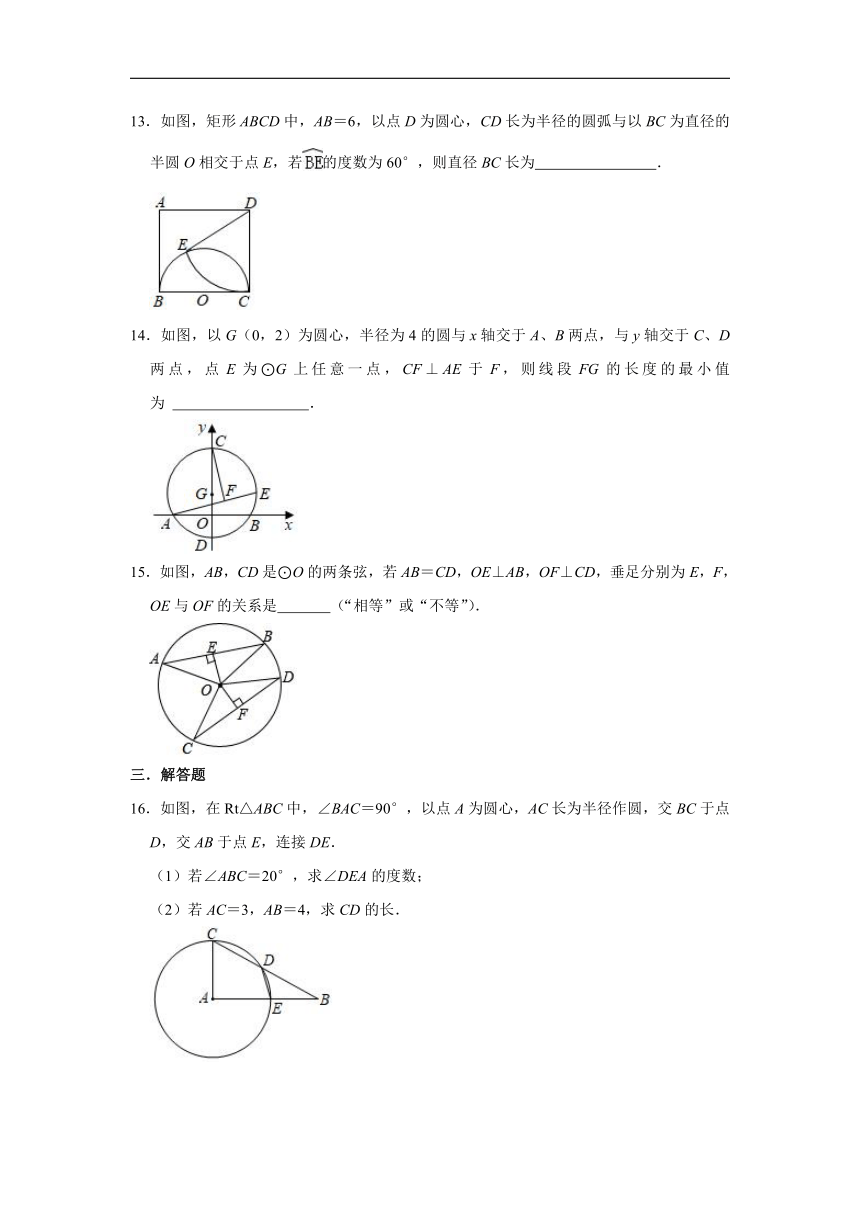
13.如图,矩形ABCD中,AB=6,以点D为圆心,CD长为半径的圆弧与以BC为直径的半圆O相交于点E,若的度数为60°,则直径BC长为 .
14.如图,以G(0,2)为圆心,半径为4的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上任意一点,CF⊥AE于F,则线段FG的长度的最小值为 .
15.如图,AB,CD是⊙O的两条弦,若AB=CD,OE⊥AB,OF⊥CD,垂足分别为E,F,OE与OF的关系是 (“相等”或“不等”).
三.解答题
16.如图,在Rt△ABC中,∠BAC=90°,以点A为圆心,AC长为半径作圆,交BC于点D,交AB于点E,连接DE.
(1)若∠ABC=20°,求∠DEA的度数;
(2)若AC=3,AB=4,求CD的长.
17.如图,在平行四边形ABCD中,AB=5,BC=8,BC边上的高AH=3,点P是边BC上的动点,以CP为半径的⊙C与边AD交于点E,F(点E在点F的左侧).
(1)当⊙C经过点A时,求CP的长;
(2)连接AP,当AP∥CE时,求⊙C的半径及弦EF的长.
18.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,OD交AC于点E,AD=CD.
(1)求证:OD∥BC;
(2)若AC=10,DE=4,求BC的长.
19.如图,点A、B、C在⊙O上,AB=CB=9,AD∥BC,CD⊥AD,且AD=2.
(1)求线段CD、AC的长;
(2)求⊙O的半径.
20.如图,⊙O的直径AB和弦CD相交于点E,AE=1cm,⊙O的半径为3cm,∠DEB=60°,求CD的长.
21.如图,AB、AC是⊙O的两条弦,且AB=AC,点D是的中点,连接并延长BD、CD,分别交AC、AB的延长线于点E、F.
(1)求证:DF=DE;
(2)若BD=6,CE=8,求⊙O的半径.
参考答案
一.选择题
1.解:过O作OC⊥AB于C,连接OA,则∠OCA=90°,
∵MO=6,∠OMA=30°,
∴OC=MO=3,
在Rt△OCA中,由勾股定理得:AC===4,
∵OC⊥AB,OC过O,
∴BC=AC,
即AB=2AC=2×4=8,
故选:D.
2.解:如图,连接AE,AF,OA,OB,过点O作OT⊥AB交⊙O于T,连接AT.
由翻折的性质可知,AB垂直平分线段OT,
∴AO=AT,
∵OA=OT,
∴△AOT是等边三角形,
∴∠AOT=60°,
∵OT⊥AB,
∴=,
∴∠AOT=∠BOT=60°,
∴∠AOB=120°,
∴∠E=∠AOB=60°,
∵∠ABF=∠ABE,
∴=,
∴AE=AF,
∴△AEF是等边三角形,
∵BF=2EF,
∴可以假设EF=2a,BF=4a,则EH=FH=a,AH=a,BH=5a,
在Rt△AHB中,AB2=AH2+BH2,
∴(2)2=(a)2+(5a)2,
∴a=1,
∴BE=6a=6,
故选:D.
3.解:∵∠AOE=60°,
∴∠BOE=180°﹣∠AOE=120°,
∴的度数是120°,
∵点C、D是的三等分点,
∴的度数是×120°=80°,
∴∠BOD=80°,
故选:C.
4.解:连接AO,
∵OC⊥AB,∴D为AB的中点,
∴AD=4cm,
设圆的半径为rcm,
在Rt△AOD中,OD=OC﹣CD=(r﹣2)cm,
根据勾股定理得:OA2=AD2+OD2,即r2=16+(r﹣2)2,
解得:r=5,
故选:C.
5.解:连OC,如图,
∵C是的中点,∠AOB=120°,
∴∠AOC=∠BOC=60°,
又∵OA=OC=OB,
∴△OAC和△OBC都是等边三角形,
∴S四边形AOBC=2×=.
故选:D.
6.解:作CM⊥AB于M,DN⊥AB于N,连接OC,OD,
∴∠NDP=∠MCP=∠APC=45°
又∵OC=OD,
∴∠ODP=∠OCP,
∵∠COM=45°+∠OCD,∠ODN=45°+∠ODC,
∴∠NDO=∠COM,
在Rt△ODN与Rt△COM中,
,
∴Rt△ODN≌Rt△COM,
∴ON=CM=PM,OM=ND=PN
又∵OC2=CM2+OM2,OD2=DN2+ON2
∴OC2=CM2+PN2,OD2=DN2+PM2
∴OC2+OD2=CM2+PN2+DN2+PM2=PC2+PD2=8
∴OC2=4,
∴OC=2,
故选:B.
7.解:
过O作OE⊥AB于E,
则∠OEB=90°,AB=DC=3.2m,
由垂径定理得:AE=BE=m=1.6m,
在Rt△BEO中,∠BEO=90°,BE=1.6m,OB=3.4m,由勾股定理得:OE==3(m),
即连车带货一起最高为3m,
故选:A.
二.填空题
8.解:如图,连接OD,AC.
∵BA=BE=BC,
∴点B是△AEC的外接圆的圆心,
∴∠ACE=∠ABE=45°,
∴∠AOD=2∠ACE=90°,
∵OA=OD=5,
∴AD=5,
故答案为:5.
9.解:过O作OM⊥AB于M,ON⊥BC于N,OQ⊥AC于Q,连接OK、OD、OF、OB、OC,设AB,AC,BC与⊙O的另一个交点分别为E,H,G.
由垂径定理得:DM=DE,KQ=KH,FN=FG,
∵DE=FG=HK,
∴DM=KQ=FN,
∵OD=OK=OF,
∴由勾股定理得:OM=ON=OQ,
即O到三角形ABC三边的距离相等,
∴O是△ABC的内心,
∴∠OBC+∠OCB=(180°﹣70°)=55°,
∴∠BOC=125°,
故答案为125°.
10.解:如下图,连接AM,连接MB,
∵∠BAD=∠CDA=90°,
∴AM过圆心O,
而A、D、M、B四点共圆,
∴四边形ADMB为矩形,而AB=1,CD=2,
∴CM=2﹣1=1=AB=DM,即:①DM=CM,正确;
又AB∥CD,
∴四边形ABMC为平行四边形,
∴∠AEB=∠MAE,=,故②正确;
∵四边形ADMB为矩形,
∴AB=DM,
∴=,
∴∠DAM=∠AMB,
过点O作OG⊥AD于G,OH⊥AE于H,
∴OG=OH,
∴AD=AE,
∴④正确;
由题设条件求不出直径的大小,
故③⊙O的直径为2,错误;
故答案为①②④.
11.解:∵AB是半圆O的直径,
∴∠ACB=90°,
∵∠BAC=46°,
∴∠B=44°.
∴∠ADC=180°﹣44°=136°.
∵=,
∴AD=DC.
∴∠DAC=∠DCA==22°,
∴∠BAD=∠DAC+∠BAC=22°+46°=68°.
故答案是:68.
12.解:如图,过点O作OE⊥AB,OF⊥CD,垂足为E、F,连接OA,
则AE=BE=AB=,CF=DF=CD=,
在Rt△AOE中,
∵OA=2,AE=,
∴OE==1,
∵AB=CD,
∴OE=OF=1,
又∵OM=OM,
∴Rt△OEM≌Rt△OFM(HL),
∴∠OME=∠OMF=∠AMC=60°,
∴OM=,
故答案为:.
13.解:如图,连接BE,EC.
∵BC是直径,
∴∠BEC=90°,
∵的度数=60°,
∴∠BCE=×60°=30°,
∵四边形ABCD是矩形,
∴AB=CD=6,∠DCB=90°,
∴∠DCE=90°﹣30°=60°,
∵DE=DC,
∴△DEC是等边三角形,
∴EC=CD=6,
∴BC=4.
故答案为:.
14.解:连接AC,过点G作GM⊥AC于M,连接AG、MF、GF,如图所示:
∵G(0,2),
∴OG=2,GO⊥AB,
∴OA=OB=AB,
∵⊙G半径为4,
∴AG=CG=4,
∴∠GCA=∠GAC,
在Rt△OAG中,==,OA==2,
∴∠OAG=30°,AB=2OA=4,
∴∠AGO=90°﹣30°=60°,
∵∠AGO=∠GCA+∠GAC=60°,
∴∠GCA=∠GAC=30°,
∴OA=AC,
∴AC=2OA=4,MG=AG=×4=2,
∵∠AFC=90°,
∴点F在以AC为直径的⊙M上,
∵GM⊥AC,
∴AM=CM,
∴MF=AC=2,
当点F在MG的延长线上时,FG的长度的最小,
最小值为:FM﹣MG=2﹣2,
故答案为:2﹣2.
15.解:∵OE⊥AB,OF⊥CD,
∴AE=EB,CF=DF,
∵AB=CD,
∴AE=CF,
∵OA=OC,∠AEO=∠CFO,AE=CF,
∴Rt△AEO≌Rt△CFO(HL),
∴OE=OF.
故答案为:相等.
三.解答题
16.解:(1)如图,连接AD.
∵∠BAC=90°,∠ABC=20°,
∴∠ACD=70°.
∵AC=AD,
∴∠ACD=∠ADC=70°,
∴∠CAD=180°﹣70°﹣70°=40°,
∴∠DAE=90°﹣40°=50°.
又∵AD=AE,
∴.
(2)如图,过点A作AF⊥CD,垂足为F.
∵∠BAC=90°,AC=3,AB=4,
∴BC=5.
又∵ AF BC= AC AB,
∴,
∴.
∵AC=AD,AF⊥CD,
∴.
17.解:(1)连接AC,如图1所示:∵AH⊥BC,
∴∠AHB=∠AHC=90°,
∴BH===4,
∴CH=BC﹣BH=4,
∴CA==5,
当⊙C经过点A时,CP=CA=5;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,当AP∥CE时,四边形APCE是平行四边形,
∵CP=CE,
∴四边形APCE是菱形,
∴PA=CP,
设PA=CP=x,则PH=4﹣x,
在Rt△APH中,
由勾股定理得:AH2+PH2=PA2,
即32+(4﹣x)2=x2,
解得:x=,
即⊙C的半径为,
作CM⊥EF于M,如图2所示:则CM=AH=3,ME=MF=EF,
在Rt△CEM中,由勾股定理得:ME===,
∴EF=2ME=.
18.(1)证明:∵AD=DC,
∴=,
∴OD⊥AC,
∴∠AEO=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠AEO=∠ACB,
∴OD∥BC.
(2)解:∵OD⊥AC,
∴AE=EC=5,
设OA=OD=r,
在Rt△AOE中,OA2=AE2+OE2,
∴r2=52+(r﹣4)2,
∴r=,
∴OE=r﹣DE=﹣4=,
∵AE=EC,AO=OB,
∴BC=2OE=.
19.解:(1)作AE⊥BC于E,如图1所示:
则AE=DC,EC=AD=2,
∴BE=BC﹣EC=9﹣2=7,
∴CD=AE===4,
∴AC===6;
(2)作BF⊥AC于F,连接OA,如图2所示:
则AF=CF=AC=3,
∴BF垂直平分AC,
∴BF一定过圆心O,BF===6,
设⊙O的半径为r,则OF=6﹣r,
在Rt△OAF中,由勾股定理得:(6﹣r)2+32=r2,
解得:r=,
即⊙O的半径为.
20.解:作OP⊥CD于P,连接OD,如图所示:
则CP=PD=CD,
∵AE=1cm,⊙O的半径为3cm,
∴OE=OA﹣AE=2cm,
在Rt△OPE中,∠DEB=60°,
∴∠POE=30°,
∴PE=OE=1cm,OP=PE=cm,
∴PD===(cm),
∴CD=2PD=2cm.
21.(1)证明:连接AD,
∵点D是的中点,
∴∠CAD=∠BAD,
∴CD=BD,
在△CAD和△BAD中,
,
∴△CAD≌△BAD(SAS),
∴∠ACD=∠ABD,
∴∠DCE=∠DBF,
在△CED和△BFD中,
,
∴△CED≌△BFD(ASA),
∴DF=DE;
(2)解:∵四边形ABDC是圆内接四边形,
∴∠DBF=∠ACD,
∵∠ACD=∠ABD,
∴∠ABD=∠DBF,
∴∠ABD=90°,
∴∠ECD=∠ABD=90°,
∴AD是⊙O的直径,
∵CD=BD=6,CE=8,
∴DE==10,
∴EB=10+6=16,
在Rt△ABE中,AB2+BE2=AE2,
设AB=AC=x,则x2+162=(x+8)2,
解得x=12,
∴AB=12,
在Rt△ABD中,AB2+BD2=AD2,
∴AD==6,
∴⊙O的半径为3.
一.选择题
1.⊙O的半径为5,M是圆外一点,MO=6,∠OMA=30°,则弦AB的长为( )
A.4 B.6 C.6 D.8
2.如图,在⊙O中将弧AB沿弦AB翻折经过圆心O交弦BE于点F,BF=2EF,AB=2,则BE长为( )
A.4 B.3 C.3 D.6
3.如图,AB为⊙O的直径,点C、D是的三等分点,∠AOE=60°,则∠BOD的度数为( )
A.40° B.60° C.80° D.120°
4.如图,是某供水管道的截面图,里面尚有一些水,若液面宽度AB=8cm,半径OC⊥AB于D,液面深度CD=2cm,则该管道的半径长为( )
A.6cm B.5.5cm C.5cm D.4cm
5.如图,A,B是⊙O上的点,∠AOB=120°,C是的中点,若⊙O的半径为5,则四边形ACBO的面积为( )
A.25 B.25 C. D.
6.如图,⊙O的直径AB与弦CD相交于点P,且∠APC=45°,若PC2+PD2=8,则⊙O的半径为( )
A. B.2 C.2 D.4
7.如图,某隧道的截面是一个半径为3.4m的半圆形,一辆宽3.2m的卡车恰好能通过该隧道,连车带货一起最高为多少米( )
A.3m B.3.4m C.4m D.2.8m
二.填空题(
8.已知四边形ABCD内接于⊙O,OA=5,AB=BC,E为CD上一点,且BE=BC,∠ABE=90°,则AD的长为 .
9.如图,△ABC中,∠A=70°,⊙O截△ABC的三条边所截得弦长相等,则∠BOC= .
10.如图,在四边形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,过A,B,D三点的⊙O分别交BC,CD于点E,M,下列结论:①DM=CM;②;③⊙O的直径为2;④AE=AD.其中正确的结论有 (填序号).
11.如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=46°,=,则
∠DAB= °.
12.如图,在半径为2的⊙O中,弦AB与弦CD相交于点M,如果AB=CD=2,∠AMC=120°,那么OM的长为 .
13.如图,矩形ABCD中,AB=6,以点D为圆心,CD长为半径的圆弧与以BC为直径的半圆O相交于点E,若的度数为60°,则直径BC长为 .
14.如图,以G(0,2)为圆心,半径为4的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上任意一点,CF⊥AE于F,则线段FG的长度的最小值为 .
15.如图,AB,CD是⊙O的两条弦,若AB=CD,OE⊥AB,OF⊥CD,垂足分别为E,F,OE与OF的关系是 (“相等”或“不等”).
三.解答题
16.如图,在Rt△ABC中,∠BAC=90°,以点A为圆心,AC长为半径作圆,交BC于点D,交AB于点E,连接DE.
(1)若∠ABC=20°,求∠DEA的度数;
(2)若AC=3,AB=4,求CD的长.
17.如图,在平行四边形ABCD中,AB=5,BC=8,BC边上的高AH=3,点P是边BC上的动点,以CP为半径的⊙C与边AD交于点E,F(点E在点F的左侧).
(1)当⊙C经过点A时,求CP的长;
(2)连接AP,当AP∥CE时,求⊙C的半径及弦EF的长.
18.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,OD交AC于点E,AD=CD.
(1)求证:OD∥BC;
(2)若AC=10,DE=4,求BC的长.
19.如图,点A、B、C在⊙O上,AB=CB=9,AD∥BC,CD⊥AD,且AD=2.
(1)求线段CD、AC的长;
(2)求⊙O的半径.
20.如图,⊙O的直径AB和弦CD相交于点E,AE=1cm,⊙O的半径为3cm,∠DEB=60°,求CD的长.
21.如图,AB、AC是⊙O的两条弦,且AB=AC,点D是的中点,连接并延长BD、CD,分别交AC、AB的延长线于点E、F.
(1)求证:DF=DE;
(2)若BD=6,CE=8,求⊙O的半径.
参考答案
一.选择题
1.解:过O作OC⊥AB于C,连接OA,则∠OCA=90°,
∵MO=6,∠OMA=30°,
∴OC=MO=3,
在Rt△OCA中,由勾股定理得:AC===4,
∵OC⊥AB,OC过O,
∴BC=AC,
即AB=2AC=2×4=8,
故选:D.
2.解:如图,连接AE,AF,OA,OB,过点O作OT⊥AB交⊙O于T,连接AT.
由翻折的性质可知,AB垂直平分线段OT,
∴AO=AT,
∵OA=OT,
∴△AOT是等边三角形,
∴∠AOT=60°,
∵OT⊥AB,
∴=,
∴∠AOT=∠BOT=60°,
∴∠AOB=120°,
∴∠E=∠AOB=60°,
∵∠ABF=∠ABE,
∴=,
∴AE=AF,
∴△AEF是等边三角形,
∵BF=2EF,
∴可以假设EF=2a,BF=4a,则EH=FH=a,AH=a,BH=5a,
在Rt△AHB中,AB2=AH2+BH2,
∴(2)2=(a)2+(5a)2,
∴a=1,
∴BE=6a=6,
故选:D.
3.解:∵∠AOE=60°,
∴∠BOE=180°﹣∠AOE=120°,
∴的度数是120°,
∵点C、D是的三等分点,
∴的度数是×120°=80°,
∴∠BOD=80°,
故选:C.
4.解:连接AO,
∵OC⊥AB,∴D为AB的中点,
∴AD=4cm,
设圆的半径为rcm,
在Rt△AOD中,OD=OC﹣CD=(r﹣2)cm,
根据勾股定理得:OA2=AD2+OD2,即r2=16+(r﹣2)2,
解得:r=5,
故选:C.
5.解:连OC,如图,
∵C是的中点,∠AOB=120°,
∴∠AOC=∠BOC=60°,
又∵OA=OC=OB,
∴△OAC和△OBC都是等边三角形,
∴S四边形AOBC=2×=.
故选:D.
6.解:作CM⊥AB于M,DN⊥AB于N,连接OC,OD,
∴∠NDP=∠MCP=∠APC=45°
又∵OC=OD,
∴∠ODP=∠OCP,
∵∠COM=45°+∠OCD,∠ODN=45°+∠ODC,
∴∠NDO=∠COM,
在Rt△ODN与Rt△COM中,
,
∴Rt△ODN≌Rt△COM,
∴ON=CM=PM,OM=ND=PN
又∵OC2=CM2+OM2,OD2=DN2+ON2
∴OC2=CM2+PN2,OD2=DN2+PM2
∴OC2+OD2=CM2+PN2+DN2+PM2=PC2+PD2=8
∴OC2=4,
∴OC=2,
故选:B.
7.解:
过O作OE⊥AB于E,
则∠OEB=90°,AB=DC=3.2m,
由垂径定理得:AE=BE=m=1.6m,
在Rt△BEO中,∠BEO=90°,BE=1.6m,OB=3.4m,由勾股定理得:OE==3(m),
即连车带货一起最高为3m,
故选:A.
二.填空题
8.解:如图,连接OD,AC.
∵BA=BE=BC,
∴点B是△AEC的外接圆的圆心,
∴∠ACE=∠ABE=45°,
∴∠AOD=2∠ACE=90°,
∵OA=OD=5,
∴AD=5,
故答案为:5.
9.解:过O作OM⊥AB于M,ON⊥BC于N,OQ⊥AC于Q,连接OK、OD、OF、OB、OC,设AB,AC,BC与⊙O的另一个交点分别为E,H,G.
由垂径定理得:DM=DE,KQ=KH,FN=FG,
∵DE=FG=HK,
∴DM=KQ=FN,
∵OD=OK=OF,
∴由勾股定理得:OM=ON=OQ,
即O到三角形ABC三边的距离相等,
∴O是△ABC的内心,
∴∠OBC+∠OCB=(180°﹣70°)=55°,
∴∠BOC=125°,
故答案为125°.
10.解:如下图,连接AM,连接MB,
∵∠BAD=∠CDA=90°,
∴AM过圆心O,
而A、D、M、B四点共圆,
∴四边形ADMB为矩形,而AB=1,CD=2,
∴CM=2﹣1=1=AB=DM,即:①DM=CM,正确;
又AB∥CD,
∴四边形ABMC为平行四边形,
∴∠AEB=∠MAE,=,故②正确;
∵四边形ADMB为矩形,
∴AB=DM,
∴=,
∴∠DAM=∠AMB,
过点O作OG⊥AD于G,OH⊥AE于H,
∴OG=OH,
∴AD=AE,
∴④正确;
由题设条件求不出直径的大小,
故③⊙O的直径为2,错误;
故答案为①②④.
11.解:∵AB是半圆O的直径,
∴∠ACB=90°,
∵∠BAC=46°,
∴∠B=44°.
∴∠ADC=180°﹣44°=136°.
∵=,
∴AD=DC.
∴∠DAC=∠DCA==22°,
∴∠BAD=∠DAC+∠BAC=22°+46°=68°.
故答案是:68.
12.解:如图,过点O作OE⊥AB,OF⊥CD,垂足为E、F,连接OA,
则AE=BE=AB=,CF=DF=CD=,
在Rt△AOE中,
∵OA=2,AE=,
∴OE==1,
∵AB=CD,
∴OE=OF=1,
又∵OM=OM,
∴Rt△OEM≌Rt△OFM(HL),
∴∠OME=∠OMF=∠AMC=60°,
∴OM=,
故答案为:.
13.解:如图,连接BE,EC.
∵BC是直径,
∴∠BEC=90°,
∵的度数=60°,
∴∠BCE=×60°=30°,
∵四边形ABCD是矩形,
∴AB=CD=6,∠DCB=90°,
∴∠DCE=90°﹣30°=60°,
∵DE=DC,
∴△DEC是等边三角形,
∴EC=CD=6,
∴BC=4.
故答案为:.
14.解:连接AC,过点G作GM⊥AC于M,连接AG、MF、GF,如图所示:
∵G(0,2),
∴OG=2,GO⊥AB,
∴OA=OB=AB,
∵⊙G半径为4,
∴AG=CG=4,
∴∠GCA=∠GAC,
在Rt△OAG中,==,OA==2,
∴∠OAG=30°,AB=2OA=4,
∴∠AGO=90°﹣30°=60°,
∵∠AGO=∠GCA+∠GAC=60°,
∴∠GCA=∠GAC=30°,
∴OA=AC,
∴AC=2OA=4,MG=AG=×4=2,
∵∠AFC=90°,
∴点F在以AC为直径的⊙M上,
∵GM⊥AC,
∴AM=CM,
∴MF=AC=2,
当点F在MG的延长线上时,FG的长度的最小,
最小值为:FM﹣MG=2﹣2,
故答案为:2﹣2.
15.解:∵OE⊥AB,OF⊥CD,
∴AE=EB,CF=DF,
∵AB=CD,
∴AE=CF,
∵OA=OC,∠AEO=∠CFO,AE=CF,
∴Rt△AEO≌Rt△CFO(HL),
∴OE=OF.
故答案为:相等.
三.解答题
16.解:(1)如图,连接AD.
∵∠BAC=90°,∠ABC=20°,
∴∠ACD=70°.
∵AC=AD,
∴∠ACD=∠ADC=70°,
∴∠CAD=180°﹣70°﹣70°=40°,
∴∠DAE=90°﹣40°=50°.
又∵AD=AE,
∴.
(2)如图,过点A作AF⊥CD,垂足为F.
∵∠BAC=90°,AC=3,AB=4,
∴BC=5.
又∵ AF BC= AC AB,
∴,
∴.
∵AC=AD,AF⊥CD,
∴.
17.解:(1)连接AC,如图1所示:∵AH⊥BC,
∴∠AHB=∠AHC=90°,
∴BH===4,
∴CH=BC﹣BH=4,
∴CA==5,
当⊙C经过点A时,CP=CA=5;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,当AP∥CE时,四边形APCE是平行四边形,
∵CP=CE,
∴四边形APCE是菱形,
∴PA=CP,
设PA=CP=x,则PH=4﹣x,
在Rt△APH中,
由勾股定理得:AH2+PH2=PA2,
即32+(4﹣x)2=x2,
解得:x=,
即⊙C的半径为,
作CM⊥EF于M,如图2所示:则CM=AH=3,ME=MF=EF,
在Rt△CEM中,由勾股定理得:ME===,
∴EF=2ME=.
18.(1)证明:∵AD=DC,
∴=,
∴OD⊥AC,
∴∠AEO=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠AEO=∠ACB,
∴OD∥BC.
(2)解:∵OD⊥AC,
∴AE=EC=5,
设OA=OD=r,
在Rt△AOE中,OA2=AE2+OE2,
∴r2=52+(r﹣4)2,
∴r=,
∴OE=r﹣DE=﹣4=,
∵AE=EC,AO=OB,
∴BC=2OE=.
19.解:(1)作AE⊥BC于E,如图1所示:
则AE=DC,EC=AD=2,
∴BE=BC﹣EC=9﹣2=7,
∴CD=AE===4,
∴AC===6;
(2)作BF⊥AC于F,连接OA,如图2所示:
则AF=CF=AC=3,
∴BF垂直平分AC,
∴BF一定过圆心O,BF===6,
设⊙O的半径为r,则OF=6﹣r,
在Rt△OAF中,由勾股定理得:(6﹣r)2+32=r2,
解得:r=,
即⊙O的半径为.
20.解:作OP⊥CD于P,连接OD,如图所示:
则CP=PD=CD,
∵AE=1cm,⊙O的半径为3cm,
∴OE=OA﹣AE=2cm,
在Rt△OPE中,∠DEB=60°,
∴∠POE=30°,
∴PE=OE=1cm,OP=PE=cm,
∴PD===(cm),
∴CD=2PD=2cm.
21.(1)证明:连接AD,
∵点D是的中点,
∴∠CAD=∠BAD,
∴CD=BD,
在△CAD和△BAD中,
,
∴△CAD≌△BAD(SAS),
∴∠ACD=∠ABD,
∴∠DCE=∠DBF,
在△CED和△BFD中,
,
∴△CED≌△BFD(ASA),
∴DF=DE;
(2)解:∵四边形ABDC是圆内接四边形,
∴∠DBF=∠ACD,
∵∠ACD=∠ABD,
∴∠ABD=∠DBF,
∴∠ABD=90°,
∴∠ECD=∠ABD=90°,
∴AD是⊙O的直径,
∵CD=BD=6,CE=8,
∴DE==10,
∴EB=10+6=16,
在Rt△ABE中,AB2+BE2=AE2,
设AB=AC=x,则x2+162=(x+8)2,
解得x=12,
∴AB=12,
在Rt△ABD中,AB2+BD2=AD2,
∴AD==6,
∴⊙O的半径为3.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
