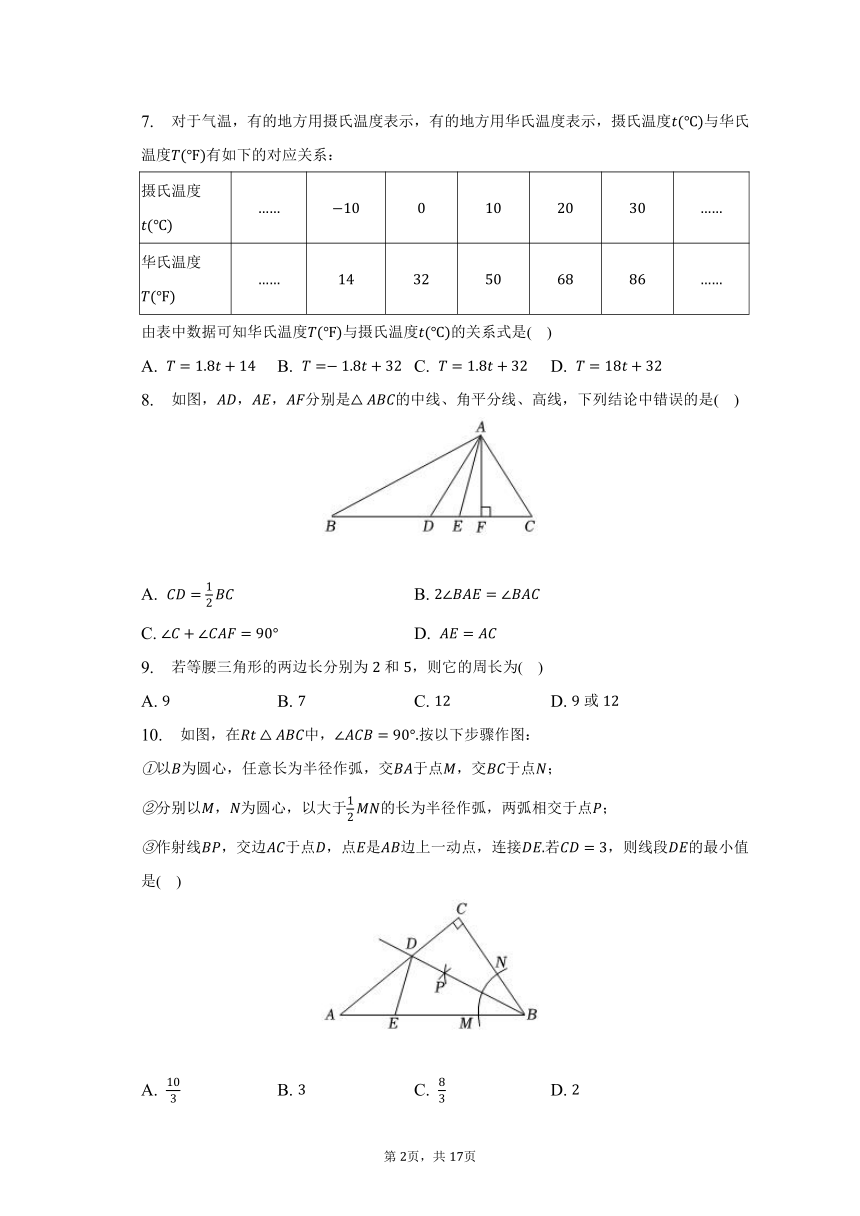
2022-2023学年山东省枣庄市山亭区、市中区七年级(下)期末数学试卷(含解析)
文档属性
| 名称 | 2022-2023学年山东省枣庄市山亭区、市中区七年级(下)期末数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 284.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-13 15:35:21 | ||
图片预览


文档简介
2022-2023学年山东省枣庄市山亭区、市中区七年级(下)期末数学试卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列式子运算正确的是( )
A. B. C. D.
2. “二十四节气”是中华农耕文明的结晶,被国际气象界誉为“中国第五大发明”下列四幅作品分别代表“立春”、“谷雨”、“白露”、“大雪”,其中不是轴对称图形的是( )
A. B. C. D.
3. 航空工业作为“现代工业之花”,对航空材料的选取有极高的要求我国科研人员攻克技术难题,已经能将航空发动机风扇叶片关键曲面轮廓误差控制在以内用科学记数法表示为( )
A. B. C. D.
4. 如图,,平分,若,则的度数为( )
A.
B.
C.
D.
5. 用下列长度的三根木棒首尾相接,能做成三角形框架的是( )
A. ,, B. ,,
C. ,, D. ,,
6. 如图,在和中,点,,,在同一直线上,,,只添加一个条件,不能判定≌的是( )
A.
B.
C.
D.
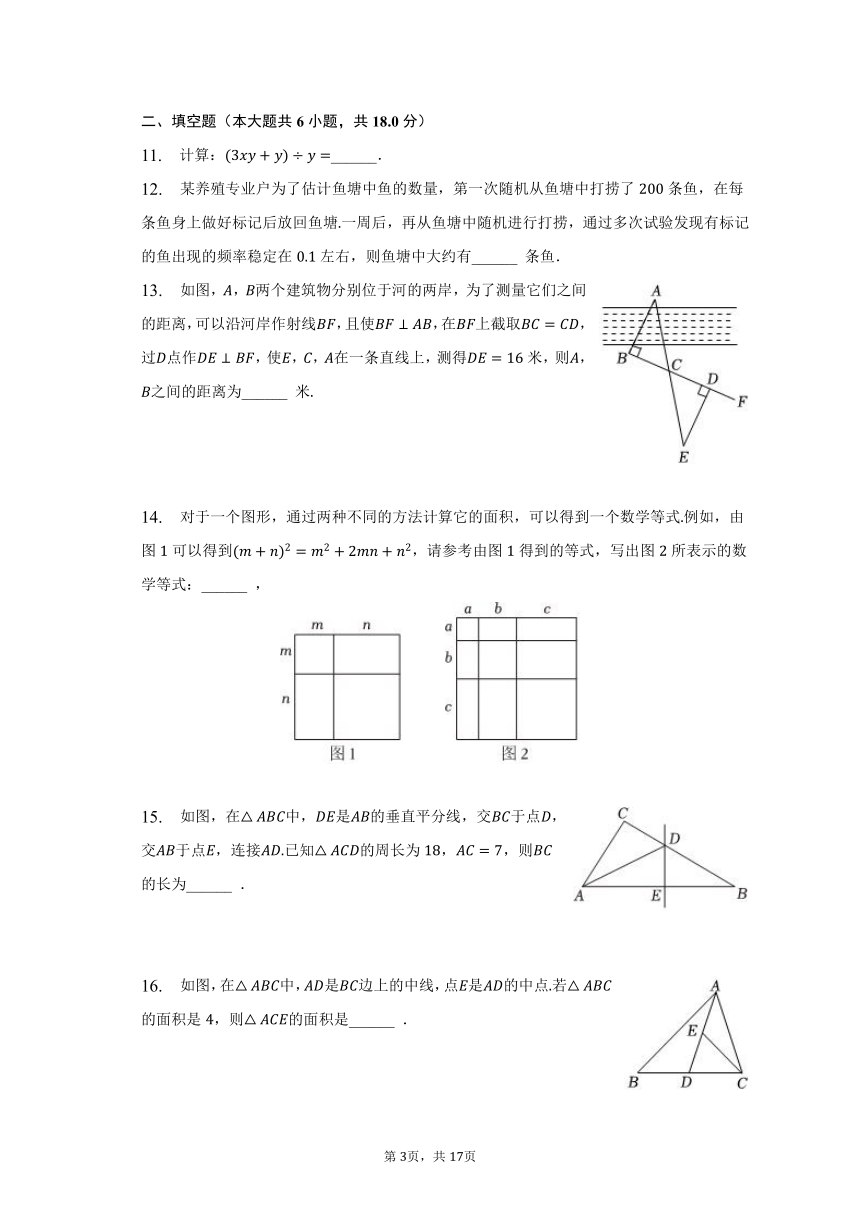
7. 对于气温,有的地方用摄氏温度表示,有的地方用华氏温度表示,摄氏温度与华氏温度有如下的对应关系:
摄氏温度
华氏温度
由表中数据可知华氏温度与摄氏温度的关系式是( )
A. B. C. D.
8. 如图,,,分别是的中线、角平分线、高线,下列结论中错误的是( )
A. B.
C. D.
9. 若等腰三角形的两边长分别为和,则它的周长为( )
A. B. C. D. 或
10. 如图,在中,按以下步骤作图:
以为圆心,任意长为半径作弧,交于点,交于点;
分别以,为圆心,以大于的长为半径作弧,两弧相交于点;
作射线,交边于点,点是边上一动点,连接若,则线段的最小值是( )
A. B. C. D.
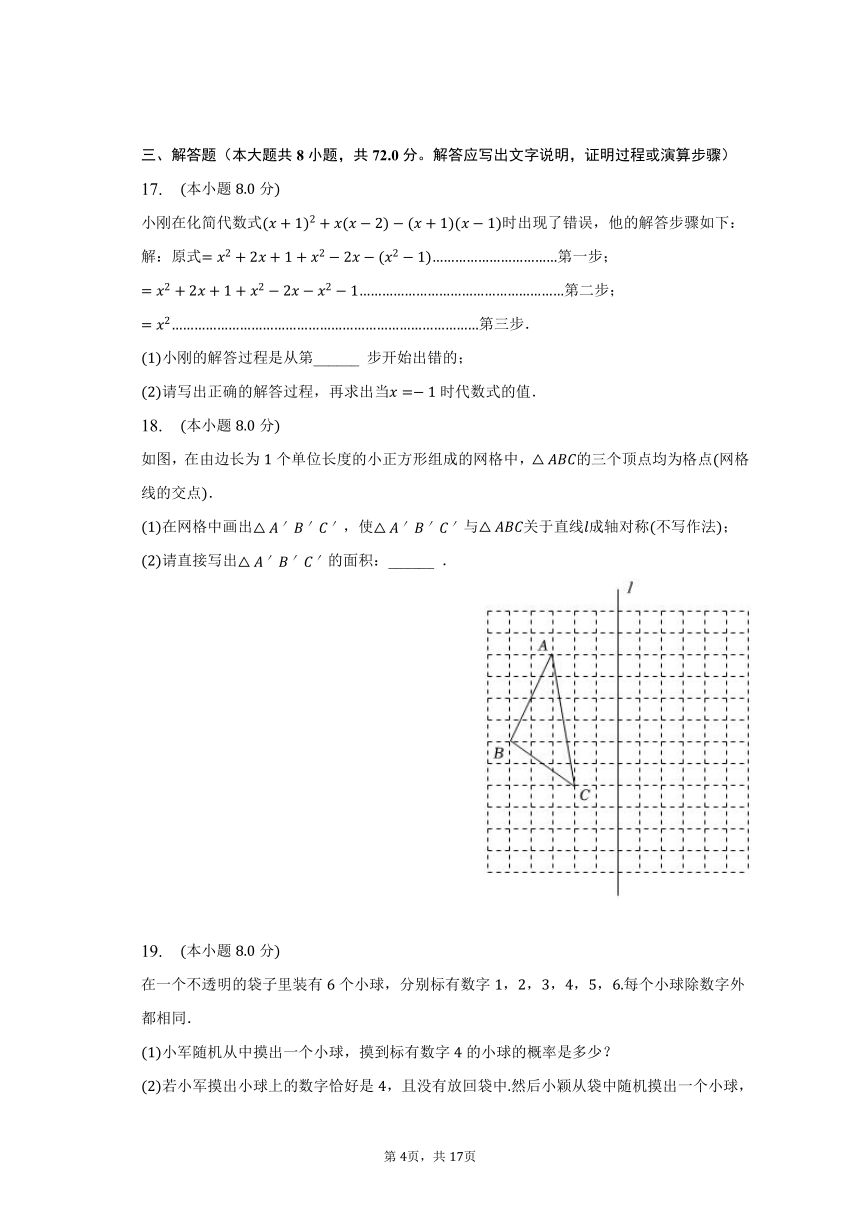
二、填空题(本大题共6小题,共18.0分)
11. 计算:______.
12. 某养殖专业户为了估计鱼塘中鱼的数量,第一次随机从鱼塘中打捞了条鱼,在每条鱼身上做好标记后放回鱼塘一周后,再从鱼塘中随机进行打捞,通过多次试验发现有标记的鱼出现的频率稳定在左右,则鱼塘中大约有______ 条鱼.
13. 如图,,两个建筑物分别位于河的两岸,为了测量它们之间的距离,可以沿河岸作射线,且使,在上截取,过点作,使,,在一条直线上,测得米,则,之间的距离为______ 米
14. 对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式例如,由图可以得到,请参考由图得到的等式,写出图所表示的数学等式:______ ,
15. 如图,在中,是的垂直平分线,交于点,交于点,连接已知的周长为,,则的长为______ .
16. 如图,在中,是边上的中线,点是的中点若的面积是,则的面积是______ .
三、解答题(本大题共8小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
小刚在化简代数式时出现了错误,他的解答步骤如下:
解:原式第一步;
第二步;
第三步.
小刚的解答过程是从第______ 步开始出错的;
请写出正确的解答过程,再求出当时代数式的值.
18. 本小题分
如图,在由边长为个单位长度的小正方形组成的网格中,的三个顶点均为格点网格线的交点.
在网格中画出,使与关于直线成轴对称不写作法;
请直接写出的面积:______ .
19. 本小题分
在一个不透明的袋子里装有个小球,分别标有数字,,,,,每个小球除数字外都相同.
小军随机从中摸出一个小球,摸到标有数字的小球的概率是多少?
若小军摸出小球上的数字恰好是,且没有放回袋中然后小颖从袋中随机摸出一个小球,小球上的数字大于的概率是多少?
现两位同学把球全部放回,请你重新制定一个摸球规则,使得摸出小球的概率是.
20. 本小题分
小明回顾了一下用尺规作一个角等于已知角的过程:
已知:.
求作:.
作法如下:
作射线;
以点为圆心,任意长为半径作弧,分别交于点,交于点;
以点为圆心,长为半径作弧,交于点;
以点为圆心,长为半径作弧,交前弧于点;
过点作射线就是所求作的角.
请你根据以上材料完成下列问题:
完成下面说理过程将正确答案填在相应的横线上;
如图,分别连接,;
由作图可知,, ______ , ______ ,所以≌ ______ ,
所以依据
上面说理过程中的依据是:______ .
21. 本小题分
生活现象
如图,杆秤是中国最古老也是现今人们仍然在使用的衡量工具,是利用杠杆原理来称质量的简易衡器,由木制的带有秤星的秤杆、金属秤砣、提绳等组成.
数学模型
如图,是杆秤的示意图,,经测量发现,,请判断与的位置关系,并说明理由.
22. 本小题分
在三角形三个内角中,如果满足其中一个内角是另一个内角的倍时,我们称此三角形为“特征三角形”,其中内角称为“主特征角”,内角称为“次特征角”.
已知在中,,,判断是否为“特征三角形”,并说明理由;
在中,,若是“特征三角形”,且是“次特征角”,求的度数.
23. 本小题分
某生物兴趣小组到劳动教育实践基地观察某种植物生长的情况,得到植物高度厘米与观察时间天之间的关系,并画出如图所示的图象.
在这个变化过程中,自变量是______ ,因变量是______ ;
该植物从观察时起,多少天以后停止厘米长高?
当观察时间从第天到第天时,植物的高度增长多少厘米?该植物平均每天长高多少厘米?
24. 本小题分
如图,在中,,是的角平分线.
写出图中全等的三角形______ ,线段与线段的位置关系是______ ;
如图,在的条件下,过点作,垂足为,交于点,且,请说明≌的理由.
答案和解析
1.【答案】
【解析】解:、,故A错误,不符题意;
B、,正确,符合题意;
C、,故C错误,不符题意;
D、,故D错误,不符题意.
故选:.
根据同底数幂的乘除法、积的乘方、幂的乘方法则逐项判断即可.
本题考查了同底数幂的乘除法、积的乘方、幂的乘方的运用,区别各个法则的应用是解题关键.
2.【答案】
【解析】解:,,选项中的图形都能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
选项中的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
故选:.
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线成轴对称.
本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
3.【答案】
【解析】解:,
故选:.
根据科学记数法的形式改写即可.
本题主要考查科学记数法的知识,熟练掌握科学记数法的形式是解题的关键.
4.【答案】
【解析】解:,
,
,
,
平分,
,
,
.
故选:.
根据平行线性质求出的度数,根据角平分线求出的度数,根据平行线性质求出的度数即可.
本题考查了角平分线定义和平行线性质的应用,注意平行线的性质有:两条平行线被第三条直线所截,同位角相等,两条平行线被第三条直线所截,内错角相等,两条平行线被第三条直线所截,同旁内角互补.
5.【答案】
【解析】解:、,故A不符合题意;
B、,故B符合题意;
C、,故C不符合题意;
D、,故D不符合题意.
故选:.
在运用三角形三边关系判定三条线段能否构成三角形时,只要两条较短的线段长度之和大于第三条线段的长度,即可判定这三条线段能构成一个三角形,由此即可判断.
本题考查三角形的三边关系,关键是掌握三角形的三边关系定理.
6.【答案】
【解析】解:,
,
A、添加,,,分别是、的对角,不能判定≌,故A符合题意;
B、由,得到,由能判定≌,故B不符合题意;
C、添加,由判定≌,故C不符合题意;
D、添加,由判定≌,故D不符合题意.
故选:.
由平行线的判定,即可判断.
本题考查平行线的判定,关键是掌握平行线的判定方法.
7.【答案】
【解析】解:表格中的各组华氏温度与摄氏温度的对应值,都满足,
故选:.
将表格中的每一组华氏温度与摄氏温度的对应值代入选项中的关系式进行验证即可.
本题考查函数关系式,验证表格中的各组华氏温度与摄氏温度的对应值所满足与的关系式是正确解答的关键.
8.【答案】
【解析】解:、是的中线,
,
故此选项不符合题意;
B、是的角平分线,
,
C、是的高线,
,
,
故此选项不符合题意;
D、无法证得,
故此选项符合题意;
故选:.
根据三角形的中线、角平分线、高线的定义进行判断即可.
本题考查了三角形的中线、角平分线和高,熟记定义是解题的关键.
9.【答案】
【解析】解:若为腰长,为底边长,
由于,则三角形不存在;
若为腰长,则符合三角形的两边之和大于第三边.
所以这个三角形的周长为.
故选:.
求等腰三角形的周长,即是确定等腰三角形的腰与底的长求周长;题目给出等腰三角形有两条边长为和,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
本题考查了等腰三角形的性质和三角形的三边关系;题目从边的方面考查三角形,涉及分类讨论的思想方法.求三角形的周长,不能盲目地将三边长相加起来,而应养成检验三边长能否组成三角形的好习惯,把不符合题意的舍去.
10.【答案】
【解析】解:由作图过程可知:平分,
,
,
当时,线段取得最小值,此时,
故选:.
由作图过程可知:平分,根据角平分线的性质即可解决问题.
本题考查了作图基本作图,角平分线的性质,解决本题的关键是掌握基本作图方法.
11.【答案】
【解析】解:原式,
故答案为:
原式利用多项式除以单项式法则计算即可求出值.
此题考查了整式的除法,熟练掌握运算法则是解本题的关键.
12.【答案】
【解析】解:设鱼塘中有鱼条,
根据题意得,
解得,
所以估计鱼塘中有鱼条.
故答案为:.
鱼塘中有鱼条,利用频率估计概率得到,然后解方程即可.
本题考查利用频率估计概率.大量反复试验下频率稳定值即概率.用到的知识点为:概率所求情况数与总情况数之比.
13.【答案】
【解析】解:在和中,
,
≌,
.
故答案为:.
证明出这两个三角形全等,从而可得到结论.
本题考查全等三角形的应用,关键是证明三角形全等,从而得到线段相等,得到结论.
14.【答案】
【解析】解:图中,“大正方形”的边长为,因此面积为,组成“大正方形”的个部分的面积和为,
因此,
故答案为:.
用代数式表示图形中各个部分的面积,利用面积之间的和差关系得出结论
本题考查完全平方公式的几何背景,掌握完全平方公式的结构特征是正确解答的前提,用代数式表示图形中各个部分的面积是解决问题的关键.
15.【答案】
【解析】解:是的垂直平分线,
,
的周长为,
,
,
.
故答案为:.
利用线段的垂直平分线的性质可知,进而求出,于是求出的长.
本题考查线段的垂直平分线的性质,解题的关键是理解题意,灵活运用所学知识解决问题.
16.【答案】
【解析】解:是边上的中线,点是的中点.
,,
,即,
的面积是,
.
故答案为:.
根据三角形的中线的性质可得,进而可求解.
本题主要考查三角形的面积,掌握三角形中线的性质是解题的关键.
17.【答案】二
【解析】解:小刚的解答过程是从第二步开始出现错误的.
故答案为:二.
原式
.
当时,原式.
仔细检查小刚的解答过程即可得出答案;
首先利用乘法公式和整式乘法运算法则进行计算,然后再合并同类项即可得出答案,最后再将代入计算即可
此题主要考查了整式的混合运算,解答此题的关键是熟练掌握乘法公式、整式乘法的运算法则.易错点是去括号,需要注意的是如果括号前面是“”号,去掉括号,括号里面的各项都要变号.
18.【答案】
【解析】解:如图,即为所求;
的面积,
故答案为:.
根据轴对称的性质即可在网格中画出,使与关于直线成轴对称;
利用网格根据割补法即可求出的面积.
本题考查作图轴对称变换,掌握轴对称图形的画法、轴对称的性质是解决此题的关键.
19.【答案】解:共有种等可能出现的结果,其中摸出小球上数字是的只有种,
所以小军随机从中摸出一个小球,摸到标有数字的小球的概率是;
由于小军摸出小球数字是,则还剩小球上的数字还有、、、、,共种等可能出现的结果,其中大于的有种,
所以小颖从袋中随机摸出一个小球,小球上的数字大于的概率是;
规则:摸出小球上的数字小于答案不唯一.
【解析】根据概率的定义,从个小球中随机摸出球,每个球被摸到的可能性是均等的,因此一共有种等可能出现的结果,其中是数字的只有种,可求出相应的概率;
小军摸出小球数字是,则还剩小球上的数字还有、、、、共种等可能出现的结果,其中大于的有种,可求出相应的概率;
根据“摸出小球的概率是”即“摸出小球的出现的次数占次的,也就是次”,再确定摸球规则.
本题考查概率公式,理解概率的定义,掌握简单随机事件概率的计算方法是正确解答的关键.
20.【答案】 全等三角形对应角相等
【解析】解:如图,分别连接,;
由作图可知,,,,
所以≌,
所以全等三角形对应角相等,
故答案为:,,;
上面说理过程中的依据是全等三角形对应角相等.
故答案为:全等三角形对应角相等.
根据作图过程即可完成填空;
根据全等三角形的性质即可解决问题.
本题考查了作图基本作图,全等三角形的判定与性质,解决本题的关键是掌握基本作图方法.
21.【答案】解:,理由如下:
,
,
,
,
.
【解析】由可得,进而得出,再根据内错角相等,两直线平行可得答案.
本题考查了平行线的判定和性质,熟练掌握这些判定和性质解题的关键.
22.【答案】解:在中,,,
,
由于,
是“特征三角形”;
在中,,
,
由于是“特征三角形”,且是“次特征角”,
当时,即,
;
当时,即,
解得;
综上所述,或.
【解析】根据三角形内角和定理求出的度数,再根据“特征三角形”的定义进行判断即可;
根据“特征三角形”,“主特征角”和“次特征角”的定义进行计算即可.
本题考查三角形内角和定理,掌握三角形内角和是,理解“特征三角形”,“主特征角”和“次特征角”的定义是解决问题的关键.
23.【答案】观察时间 植物高度
【解析】解:根据图象可知自变量是观察时间,是因变量是植物的高度,
故答案为:观察时间,植物高度;
根据图象可知:该植物从观察时起,天以后停止长高;
因为,所以从第天到第天,植物的高度增长厘米,
,
植物平均每天长高厘米.
根据图象即可得出答案;
根据图象即可得出答案;
第天时植物的高度是厘米,第天时植物的高度是厘米
本题考查由函数图象获取信息,正确理解图象是解题的关键.
24.【答案】≌
【解析】解:是的角平分线,
,
在和中,
,
≌,
,
,
,
即,
故答案为:≌;;
由知,
,
,
,
,
,
,
在和中,
,
≌.
先根据角平分线的定义得出,然后根据可证得和全等,即可得出;
先根据同角的余角相等得出,再根据即可证得≌.
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:、、、、.
第1页,共1页
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列式子运算正确的是( )
A. B. C. D.
2. “二十四节气”是中华农耕文明的结晶,被国际气象界誉为“中国第五大发明”下列四幅作品分别代表“立春”、“谷雨”、“白露”、“大雪”,其中不是轴对称图形的是( )
A. B. C. D.
3. 航空工业作为“现代工业之花”,对航空材料的选取有极高的要求我国科研人员攻克技术难题,已经能将航空发动机风扇叶片关键曲面轮廓误差控制在以内用科学记数法表示为( )
A. B. C. D.
4. 如图,,平分,若,则的度数为( )
A.
B.
C.
D.
5. 用下列长度的三根木棒首尾相接,能做成三角形框架的是( )
A. ,, B. ,,
C. ,, D. ,,
6. 如图,在和中,点,,,在同一直线上,,,只添加一个条件,不能判定≌的是( )
A.
B.
C.
D.
7. 对于气温,有的地方用摄氏温度表示,有的地方用华氏温度表示,摄氏温度与华氏温度有如下的对应关系:
摄氏温度
华氏温度
由表中数据可知华氏温度与摄氏温度的关系式是( )
A. B. C. D.
8. 如图,,,分别是的中线、角平分线、高线,下列结论中错误的是( )
A. B.
C. D.
9. 若等腰三角形的两边长分别为和,则它的周长为( )
A. B. C. D. 或
10. 如图,在中,按以下步骤作图:
以为圆心,任意长为半径作弧,交于点,交于点;
分别以,为圆心,以大于的长为半径作弧,两弧相交于点;
作射线,交边于点,点是边上一动点,连接若,则线段的最小值是( )
A. B. C. D.
二、填空题(本大题共6小题,共18.0分)
11. 计算:______.
12. 某养殖专业户为了估计鱼塘中鱼的数量,第一次随机从鱼塘中打捞了条鱼,在每条鱼身上做好标记后放回鱼塘一周后,再从鱼塘中随机进行打捞,通过多次试验发现有标记的鱼出现的频率稳定在左右,则鱼塘中大约有______ 条鱼.
13. 如图,,两个建筑物分别位于河的两岸,为了测量它们之间的距离,可以沿河岸作射线,且使,在上截取,过点作,使,,在一条直线上,测得米,则,之间的距离为______ 米
14. 对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式例如,由图可以得到,请参考由图得到的等式,写出图所表示的数学等式:______ ,
15. 如图,在中,是的垂直平分线,交于点,交于点,连接已知的周长为,,则的长为______ .
16. 如图,在中,是边上的中线,点是的中点若的面积是,则的面积是______ .
三、解答题(本大题共8小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
小刚在化简代数式时出现了错误,他的解答步骤如下:
解:原式第一步;
第二步;
第三步.
小刚的解答过程是从第______ 步开始出错的;
请写出正确的解答过程,再求出当时代数式的值.
18. 本小题分
如图,在由边长为个单位长度的小正方形组成的网格中,的三个顶点均为格点网格线的交点.
在网格中画出,使与关于直线成轴对称不写作法;
请直接写出的面积:______ .
19. 本小题分
在一个不透明的袋子里装有个小球,分别标有数字,,,,,每个小球除数字外都相同.
小军随机从中摸出一个小球,摸到标有数字的小球的概率是多少?
若小军摸出小球上的数字恰好是,且没有放回袋中然后小颖从袋中随机摸出一个小球,小球上的数字大于的概率是多少?
现两位同学把球全部放回,请你重新制定一个摸球规则,使得摸出小球的概率是.
20. 本小题分
小明回顾了一下用尺规作一个角等于已知角的过程:
已知:.
求作:.
作法如下:
作射线;
以点为圆心,任意长为半径作弧,分别交于点,交于点;
以点为圆心,长为半径作弧,交于点;
以点为圆心,长为半径作弧,交前弧于点;
过点作射线就是所求作的角.
请你根据以上材料完成下列问题:
完成下面说理过程将正确答案填在相应的横线上;
如图,分别连接,;
由作图可知,, ______ , ______ ,所以≌ ______ ,
所以依据
上面说理过程中的依据是:______ .
21. 本小题分
生活现象
如图,杆秤是中国最古老也是现今人们仍然在使用的衡量工具,是利用杠杆原理来称质量的简易衡器,由木制的带有秤星的秤杆、金属秤砣、提绳等组成.
数学模型
如图,是杆秤的示意图,,经测量发现,,请判断与的位置关系,并说明理由.
22. 本小题分
在三角形三个内角中,如果满足其中一个内角是另一个内角的倍时,我们称此三角形为“特征三角形”,其中内角称为“主特征角”,内角称为“次特征角”.
已知在中,,,判断是否为“特征三角形”,并说明理由;
在中,,若是“特征三角形”,且是“次特征角”,求的度数.
23. 本小题分
某生物兴趣小组到劳动教育实践基地观察某种植物生长的情况,得到植物高度厘米与观察时间天之间的关系,并画出如图所示的图象.
在这个变化过程中,自变量是______ ,因变量是______ ;
该植物从观察时起,多少天以后停止厘米长高?
当观察时间从第天到第天时,植物的高度增长多少厘米?该植物平均每天长高多少厘米?
24. 本小题分
如图,在中,,是的角平分线.
写出图中全等的三角形______ ,线段与线段的位置关系是______ ;
如图,在的条件下,过点作,垂足为,交于点,且,请说明≌的理由.
答案和解析
1.【答案】
【解析】解:、,故A错误,不符题意;
B、,正确,符合题意;
C、,故C错误,不符题意;
D、,故D错误,不符题意.
故选:.
根据同底数幂的乘除法、积的乘方、幂的乘方法则逐项判断即可.
本题考查了同底数幂的乘除法、积的乘方、幂的乘方的运用,区别各个法则的应用是解题关键.
2.【答案】
【解析】解:,,选项中的图形都能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
选项中的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
故选:.
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线成轴对称.
本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
3.【答案】
【解析】解:,
故选:.
根据科学记数法的形式改写即可.
本题主要考查科学记数法的知识,熟练掌握科学记数法的形式是解题的关键.
4.【答案】
【解析】解:,
,
,
,
平分,
,
,
.
故选:.
根据平行线性质求出的度数,根据角平分线求出的度数,根据平行线性质求出的度数即可.
本题考查了角平分线定义和平行线性质的应用,注意平行线的性质有:两条平行线被第三条直线所截,同位角相等,两条平行线被第三条直线所截,内错角相等,两条平行线被第三条直线所截,同旁内角互补.
5.【答案】
【解析】解:、,故A不符合题意;
B、,故B符合题意;
C、,故C不符合题意;
D、,故D不符合题意.
故选:.
在运用三角形三边关系判定三条线段能否构成三角形时,只要两条较短的线段长度之和大于第三条线段的长度,即可判定这三条线段能构成一个三角形,由此即可判断.
本题考查三角形的三边关系,关键是掌握三角形的三边关系定理.
6.【答案】
【解析】解:,
,
A、添加,,,分别是、的对角,不能判定≌,故A符合题意;
B、由,得到,由能判定≌,故B不符合题意;
C、添加,由判定≌,故C不符合题意;
D、添加,由判定≌,故D不符合题意.
故选:.
由平行线的判定,即可判断.
本题考查平行线的判定,关键是掌握平行线的判定方法.
7.【答案】
【解析】解:表格中的各组华氏温度与摄氏温度的对应值,都满足,
故选:.
将表格中的每一组华氏温度与摄氏温度的对应值代入选项中的关系式进行验证即可.
本题考查函数关系式,验证表格中的各组华氏温度与摄氏温度的对应值所满足与的关系式是正确解答的关键.
8.【答案】
【解析】解:、是的中线,
,
故此选项不符合题意;
B、是的角平分线,
,
C、是的高线,
,
,
故此选项不符合题意;
D、无法证得,
故此选项符合题意;
故选:.
根据三角形的中线、角平分线、高线的定义进行判断即可.
本题考查了三角形的中线、角平分线和高,熟记定义是解题的关键.
9.【答案】
【解析】解:若为腰长,为底边长,
由于,则三角形不存在;
若为腰长,则符合三角形的两边之和大于第三边.
所以这个三角形的周长为.
故选:.
求等腰三角形的周长,即是确定等腰三角形的腰与底的长求周长;题目给出等腰三角形有两条边长为和,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
本题考查了等腰三角形的性质和三角形的三边关系;题目从边的方面考查三角形,涉及分类讨论的思想方法.求三角形的周长,不能盲目地将三边长相加起来,而应养成检验三边长能否组成三角形的好习惯,把不符合题意的舍去.
10.【答案】
【解析】解:由作图过程可知:平分,
,
,
当时,线段取得最小值,此时,
故选:.
由作图过程可知:平分,根据角平分线的性质即可解决问题.
本题考查了作图基本作图,角平分线的性质,解决本题的关键是掌握基本作图方法.
11.【答案】
【解析】解:原式,
故答案为:
原式利用多项式除以单项式法则计算即可求出值.
此题考查了整式的除法,熟练掌握运算法则是解本题的关键.
12.【答案】
【解析】解:设鱼塘中有鱼条,
根据题意得,
解得,
所以估计鱼塘中有鱼条.
故答案为:.
鱼塘中有鱼条,利用频率估计概率得到,然后解方程即可.
本题考查利用频率估计概率.大量反复试验下频率稳定值即概率.用到的知识点为:概率所求情况数与总情况数之比.
13.【答案】
【解析】解:在和中,
,
≌,
.
故答案为:.
证明出这两个三角形全等,从而可得到结论.
本题考查全等三角形的应用,关键是证明三角形全等,从而得到线段相等,得到结论.
14.【答案】
【解析】解:图中,“大正方形”的边长为,因此面积为,组成“大正方形”的个部分的面积和为,
因此,
故答案为:.
用代数式表示图形中各个部分的面积,利用面积之间的和差关系得出结论
本题考查完全平方公式的几何背景,掌握完全平方公式的结构特征是正确解答的前提,用代数式表示图形中各个部分的面积是解决问题的关键.
15.【答案】
【解析】解:是的垂直平分线,
,
的周长为,
,
,
.
故答案为:.
利用线段的垂直平分线的性质可知,进而求出,于是求出的长.
本题考查线段的垂直平分线的性质,解题的关键是理解题意,灵活运用所学知识解决问题.
16.【答案】
【解析】解:是边上的中线,点是的中点.
,,
,即,
的面积是,
.
故答案为:.
根据三角形的中线的性质可得,进而可求解.
本题主要考查三角形的面积,掌握三角形中线的性质是解题的关键.
17.【答案】二
【解析】解:小刚的解答过程是从第二步开始出现错误的.
故答案为:二.
原式
.
当时,原式.
仔细检查小刚的解答过程即可得出答案;
首先利用乘法公式和整式乘法运算法则进行计算,然后再合并同类项即可得出答案,最后再将代入计算即可
此题主要考查了整式的混合运算,解答此题的关键是熟练掌握乘法公式、整式乘法的运算法则.易错点是去括号,需要注意的是如果括号前面是“”号,去掉括号,括号里面的各项都要变号.
18.【答案】
【解析】解:如图,即为所求;
的面积,
故答案为:.
根据轴对称的性质即可在网格中画出,使与关于直线成轴对称;
利用网格根据割补法即可求出的面积.
本题考查作图轴对称变换,掌握轴对称图形的画法、轴对称的性质是解决此题的关键.
19.【答案】解:共有种等可能出现的结果,其中摸出小球上数字是的只有种,
所以小军随机从中摸出一个小球,摸到标有数字的小球的概率是;
由于小军摸出小球数字是,则还剩小球上的数字还有、、、、,共种等可能出现的结果,其中大于的有种,
所以小颖从袋中随机摸出一个小球,小球上的数字大于的概率是;
规则:摸出小球上的数字小于答案不唯一.
【解析】根据概率的定义,从个小球中随机摸出球,每个球被摸到的可能性是均等的,因此一共有种等可能出现的结果,其中是数字的只有种,可求出相应的概率;
小军摸出小球数字是,则还剩小球上的数字还有、、、、共种等可能出现的结果,其中大于的有种,可求出相应的概率;
根据“摸出小球的概率是”即“摸出小球的出现的次数占次的,也就是次”,再确定摸球规则.
本题考查概率公式,理解概率的定义,掌握简单随机事件概率的计算方法是正确解答的关键.
20.【答案】 全等三角形对应角相等
【解析】解:如图,分别连接,;
由作图可知,,,,
所以≌,
所以全等三角形对应角相等,
故答案为:,,;
上面说理过程中的依据是全等三角形对应角相等.
故答案为:全等三角形对应角相等.
根据作图过程即可完成填空;
根据全等三角形的性质即可解决问题.
本题考查了作图基本作图,全等三角形的判定与性质,解决本题的关键是掌握基本作图方法.
21.【答案】解:,理由如下:
,
,
,
,
.
【解析】由可得,进而得出,再根据内错角相等,两直线平行可得答案.
本题考查了平行线的判定和性质,熟练掌握这些判定和性质解题的关键.
22.【答案】解:在中,,,
,
由于,
是“特征三角形”;
在中,,
,
由于是“特征三角形”,且是“次特征角”,
当时,即,
;
当时,即,
解得;
综上所述,或.
【解析】根据三角形内角和定理求出的度数,再根据“特征三角形”的定义进行判断即可;
根据“特征三角形”,“主特征角”和“次特征角”的定义进行计算即可.
本题考查三角形内角和定理,掌握三角形内角和是,理解“特征三角形”,“主特征角”和“次特征角”的定义是解决问题的关键.
23.【答案】观察时间 植物高度
【解析】解:根据图象可知自变量是观察时间,是因变量是植物的高度,
故答案为:观察时间,植物高度;
根据图象可知:该植物从观察时起,天以后停止长高;
因为,所以从第天到第天,植物的高度增长厘米,
,
植物平均每天长高厘米.
根据图象即可得出答案;
根据图象即可得出答案;
第天时植物的高度是厘米,第天时植物的高度是厘米
本题考查由函数图象获取信息,正确理解图象是解题的关键.
24.【答案】≌
【解析】解:是的角平分线,
,
在和中,
,
≌,
,
,
,
即,
故答案为:≌;;
由知,
,
,
,
,
,
,
在和中,
,
≌.
先根据角平分线的定义得出,然后根据可证得和全等,即可得出;
先根据同角的余角相等得出,再根据即可证得≌.
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:、、、、.
第1页,共1页
同课章节目录
